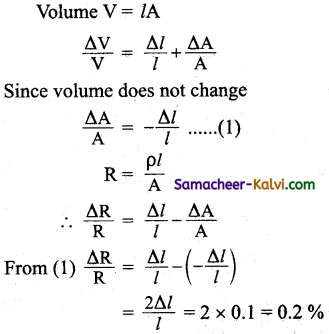Tag: Current Electricity

TN State Board 12th Physics Important Questions Chapter 2 Current Electricity

Question 1.
What is meant by Current electricity?
Answer:
Current electricity is the study of flow of electric charges.

Question 2.
What are free electrons?
Answer:
Atoms in metals have one or more electrons that are loosely bound to the nucleus. They are called free electrons.

Question 3.
What are conductors?
Answer:
Conductors are the substances that have an abundance of free electrons.

Question 4.
The positive ions will not give rise to current – Why?
Answer:
The positive ions will not move freely within the material like the free electron. So, the positive ions will not give rise to current.

Question 5.
Define one ampere.
Answer:
One ampere of current is defined as one coulomb of charge passing through a perpendicular cross-section in one second.

Question 6.
Define mobility of the electron.
Answer:
Mobility of the electron is defined as the magnitude of the drift velocity per unit electric field.
μ = \(\frac{\left|\vec{v}_{d}\right|}{|\overrightarrow{\mathrm{E}}|}\)

Question 7.
State the units of (i) drift velocity and (ii) mobility.
Answer:
(i) Unit of drift velocity m / s
(ii) Unit of mobility m² / Vs.

Question 8.
What are carbon resistors?
Answer:
Carbon resistors are the resistors containing a ceramic core on which a thin layer of i crystalline carbon is deposited.

Question 9.
What is a thermistor?
Answer:
A thermistor is a semiconductor with a negative temperature coefficient of resistance.

Question 10.
State the factors on which does the resistivity of material depends?
Answer:
(i) Number density (n) of the electrons.
(ii) The average time between two collisions.

Question 11.
What are super conductors?
Answer:
Super conductors are the materials in which their resistance becomes zero below the transition temperature.

Question 12.
Name the metals that exhibit positive Thomson effect.
Answer:
Silver Zinc and cadmium.

Question 13.
Mention the metals in which negative – Thomson effect is observed.
Answer:
Platinum, nickel, Cobalt and Mercury.

Question 14.
How is very high temperature produced in the electrical furnace?
Answer:
Very high temperatures up to 1500°C is produced in the electrical furnace by using molybdenum nichrome wire wound over a silica tube.

Question 15.
Define electric current.
Electric current in a conductor is defined as the rate of flow of charges through a given cross-sectional area.

Question 16.
Define drift velocity.
Answer:
Drift velocity is defined as the average velocity acquired by the electrons inside the conductor when it is subjected to an electric field.

Question 17.
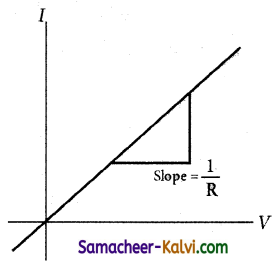
Draw the graphical representation for
(i) Ohmic conductor
Answer:

(ii) non ohmic conductor
Answer:

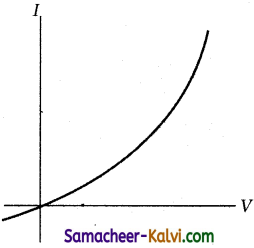
Question 18.
Define resistance. State its unit.
Answer:
Resistance is defined as the ratio of potential difference across the given conductor to the current passing through the conductor.
R = \(\frac{\mathrm{V}}{\mathrm{I}}\)
Its unit is Ohm.

Question 19.
What is meant by transition temperature?
Answer:
Transition Temperature is the temperature below which the resistance of a super conductor becomes zero.

Question 20.
Answer:
Repairing the electrical connections with wet hands is always dangerous. Give reason.
Answer:
For a human body, the resistance of dry skin is high and around 500 k Ω. But the wet skin of hands has less resistance and around 1000 Ω Ohm. Hence a large amount of current can flow through the wet hands. Hence it always dangerous.

Question 21.
Why are household appliance always connected in parallel?
Answer:
They are connected in parallel so that even if one is switched off, the other devices could function properly.

Question 22.
Distinguish electromotive force from the potential difference.
Answer:

Electromotive force	Potential difference
It is the difference of potentials between two terminals of a cell in an open circuit.	It is the difference in potentials between any two points in a closed circuit.
It is an independent of external resistance of the circuit.	It is proportional to the resistance between any two points.

Question 23.
How ohm’s law is derived from drift velocity relates current formula?
Answer:
The current flowing through a conductor is,

I = nAev_d

But v_d = \(\frac{e \mathrm{E}}{m} \cdot \tau\)

I = nAe \(\frac{e \mathrm{E}}{m} \cdot \tau\)

I = \(\frac{n \mathrm{~A} e^{2}}{m \mathrm{~L}} \tau \mathrm{V}\)

[∵ E = \(\frac{\mathrm{V}}{\mathrm{L}}\)]
where V is the potential difference. The quantity \(\frac{m \mathrm{~L}}{n \mathrm{~A} e^{2} \tau}\) is a constant for a given conductor, called electrical resistance (R).
I ∝ V
The law states that, at a constant temperature, the steady current flowing through a conductor is directly proportional to the potential difference between the two ends of the conductor.

Question 24.
In the following circuit, calculate the current through the circuit. Mention its direction.

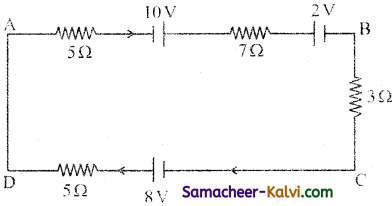
Answer:
According to kirchhofFs second law,
5i + 7i + 3i + 5i = 10 + 8 – 2
20 i = 16
i = \(\frac{16}{20}\) = \(\frac{4}{5}\) A = 0.8 A

Question 25.
State any three difference between electric power and electric energy.
Answer:

Electric power	Electric energy
(i) Electric power is defined as the rate of doing electric work.	Electric energy is defined as the capacity to do electric work.
(ii) It is the product of potential difference and current strength P = VI.	It is the product of potential difference, strength of current and time during which current flows through the conductor.
(iii) In practice it is measured by watt	In practice it is measured by watt hour or kilowatt hour.

Question 26.
The colours of a carbon resistor is orange, orange, orange. What is the value of resistor?

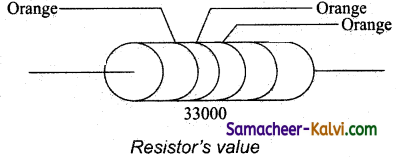
Answer:
The first orange ring corresponds to 3. The next orange ring corresponds to 3. The third orange ring corresponds to 10³. Hence the total resistance is 33 KΩ.

Question 27.
What are the special features of an ideal battery?
Answer:
(i) The internal resistance of an ideal battery is zero.
(ii) The potential difference across the battery equals to its emf.

Question 28.
State sign convention followed by Kirchhoff’s current rule.
Answer:

• Current entering the junction is taken as positive.
• Current leaving the junction is taken as negative.

Question 29.
What are the sign conventions followed by Kirchhoff’s loop rule?
Answer:

• In a loop, the product of current and resistance is taken as positive when the direction of current is followed.
• If the direction of current is opposite to the direction of the loop then the product of current and resistance across the resistor is negative.

Question 30.
Nichrome is used as a heating element in electric heaters. Give reason.
Answer:
Since nichrome has a high specific resistance. It can be heated to very high temperatures without oxidation.

Question 31.
What is meant by Joule’s heating effect.
Answer:
When current flows through a resistor, some of the electrical energy delivered to the resistor is converted into heat energy and it is dissipated.

Question 32.
What do you know about thermoelectric effect?
Answer:
Conversion of temperature differences into electrical voltage and vice versa is known as thermoelectric effect.

Question 33.
Explain drift velocity and obtain an expression for it.
Answer:
In a conductor the charge carriers are free electrons. These electrons move freely through the conductor and collide repeatedly with the positive ions.

Suppose a potential difference is set across the conductor by connecting a battery, an electric field \(\overrightarrow{\mathbf{E}}\) is created in the conductor. This electric field exerts a force on the electrons. Then it produces a current.

The electric field accelerates the electrons, while ions scatter the electrons and change the direction of motion. In this way, we have zigzag paths of electrons. In addition to the zigzag motion due to the collisions, the electrons move slowly along the conductor in a direction opposite to that of E as shown in the Figure.

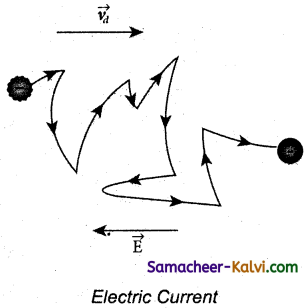
The drift velocity is the average velocity acquired by the electrons inside the conductor when it is subjected to an electric field. The average time between successive collisions is called the mean free time denoted by τ. The acceleration \(\overrightarrow{\mathbf{a}}\) experienced by the electron in an electric field \(\overrightarrow{\mathbf{E}}\) is given by

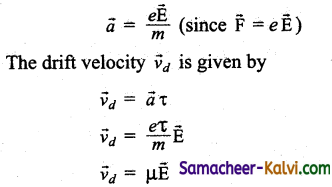
Question 34.
Describe the combination of ceils in which cells are connected
(i) in series and
(ii) in parallel. Hence obtain an expression for the current flowing in those combination of cells.
Answer:
(i) Cell in series:
Suppose n cells, each of emf ξ, volts and internal resistance r ohms are connected in series with an external resistance R.

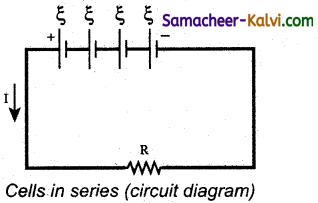
The total emf of the battery = nξ
The total resistance in the circuit = nr + R
By Ohm’s law, the ctitrent in the circuit is

I = \(\frac{\text { total emf }}{\text { total resistance }}\)

= \(\frac{n \xi}{n r+R}\)

Case (a) If r << R, then,

I = \(\frac{n \xi}{R}\) ≈ nI₁

where, I₁ is the current due to a single cell

(I₁ = \(\frac{\xi}{R}\))

Thus, if r is negligible when compared to R the current supplied by the battery is n times that supplied by a single cell.
Case (b):
If r >> R,
I = \(\frac{n \xi}{n r} \approx \frac{\xi}{r}\)

It is the current due to a single cell. That is, current due to the whole battery is the same as that due to a single cell and hence there is no advantage in connecting several cells.

Thus series connection of cells is advantageous only when the effective internal resistance of the cells is negligibly small compared with R.

(ii) Cells in parallel:
Let n cells be connected in parallel between the points A and B and a resistance R is connected between the points A and B. Let ξ be the emf and r the internal resistance of each cell.

The equivalent internal resistance of the battery is

\(\frac{1}{r_{e q}}=\frac{1}{r}+\frac{1}{r}+\frac{1}{r}+\ldots+\frac{1}{r}(n \text { terms })=\frac{n}{r}\)

So r_eq = \(\frac{r}{n}\) and the total resistance in the circuit = R + \(\frac{r}{n}\). The total emf is the potential difference between the points A and B, which is equal to ξ. The current in the circuit is given by,

I = \(\frac{\xi}{\frac{r}{n}+R}\)

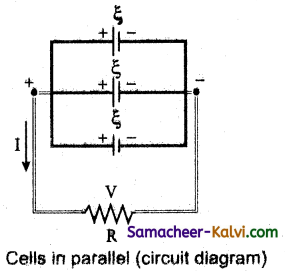
I = \(\frac{n \xi}{r+n R}\)

Case (a) If r >> R,

I = \(\frac{n \xi}{r}\) = nI₁
where I₁ is the current due to a single cell and is equal to \(\frac{\xi}{r}\) when R is negligible. Thus, the current through the external resistance due to j the whole battery is n times the current due | to a single cell.

Case (b) If r << R,
I = \(\frac{\xi}{r}\)
The above equation, It is implied from j that current due to the whole battery is the same as that due to a single cell. Hence it is advantageous to connect cells in parallel when the external resistance is very small compared to the internal resistance of the cells.

Question 35.
Describe the potentiometer and explain its principle.
Answer:
Potentiometer is used for the accurate measurement of potential differences, current and resistances.
Description:
It consists of ten meter long uniform wire of manganin or constantan (-) an stretched in parallel rows each of 1 meter length, on a wooden board. The two free ends A and B are brought to the same side and fixed to copper strips with binding screws. A meter scale is fixed parallel to the wire.

A jockey is provided for making contact. The principle of the potentiometer is illustrated in Figure. A steady current is maintained across the wire CD by a battery Bt. The battery, key and the potentiometer wire are connected in series forms the primary circuit. The positive terminal of a primary cell of emf ξ, is connected to the point C and negative terminal is connected to the jockey resistance HR. This forms the secondary circuit.

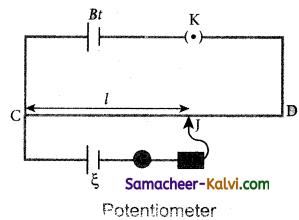
Procedure:
Let contact be made at any point J on the wire by jockey. If the potential difference across CJ is equal to the emf of the cell ξ, then no current will flow through the galvanometer and it will show zero deflection. CJ is the balancing length /. The potential difference across CJ is equal to Irl where I is the current flowing through the wire and r is the resistance per unit length of the wire.
Hence ξ = Irl ………(1)

Principle:
since I and r are constants, ξ ∝ l. The emf of the cell is directly proportional to the balancing length.

Question 36.
Explain the method of measuring internal resistance using a potentiometer.
Answer:
The end C of the potentiometer wire is connected to the positive terminal of the battery B and the negative terminal of the battery is connected to the end D through a key K₁. This forms the primary circuit.

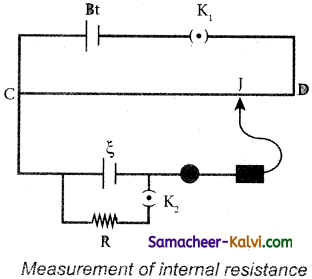
The positive terminal of the cell ξ, whose internal resistance is to be determined is also connected to the end C of the wire. The negative terminal of the cell ξ is connected to a jockey through a galvanometer and a high resistance. A resistance box R and key K₂ are connected across the cell ξ. With K₂ open, the balancing point J is obtained and the balancing length CJ = l₁ is measured. Since the cell is in open circuit, its emf is
ξ ∝ l₁ …….(1)

A suitable resistance (say, 10 Ω) is included in the resistance box and key K₂ is closed. Let r be the internal resistance of the cell. The current passing through the cell and the resistance R is given by
I = \(\frac{\xi}{\mathrm{R}+r}\)

The potential difference across R is

V = \(\frac{\xi \mathrm{R}}{\mathrm{R}+r}\)

When this potential difference is balanced on the potentiometer wire, let l₂ be the balancing length.
Then \(\frac{\xi \mathrm{R}}{\mathrm{R}+r}\) ∝ l₂ …………(2)
From equations (1) and (2)

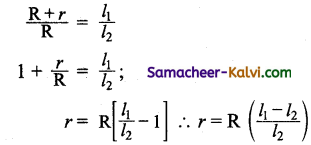
Substituting the values of the R, l₁ and l₂, the internal resistance of the cell is determined. The experiment can be repeated for different values of R. It is found that the internal resistance of the cell is not constant but increases with increase of external resistance connected across its terminals.

Question 37.
Explain Peltier effect.
Answer:

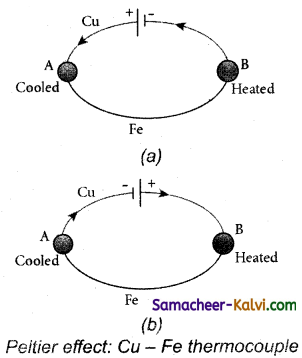
In 1834, Peltier discovered that when an electric Current is passed through a circuit of a thermocouple, heat is evolved at one junction and absorbed at the other junction. This is known as Peltier effect.In the Cu-Fe thermocouple the junctions A and B are maintained at the same temperature. Let a current from a battery flow through the thermocouple (Figure (a)).

At the junction A, where the current flows from Cu to Fe, heat is absorbed and the junction A becomes cold. At the junction B, where the current flows from Fe to Cu heat is liberated and it becomes hot. When the direction of current is reversed, junction A gets heated and junction B gets cooled as shown in the Figure (b). Hence peltier effect is reversible.

Question 38.
Explain Thomson effect.
Answer:
Thomson showed that if two points in a conductor are at different temperatures, the density of electrons at these points will differ and as a result the potential difference is created between these points. Thomson effect is also reversible.

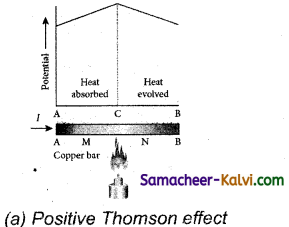
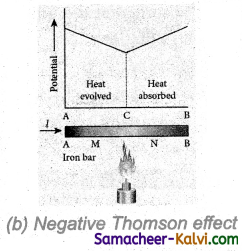
If current is passed through a copper bar AB which is heated at the middle point C, the point C will be at higher potential. This indicates that the heat is absorbed along AC and evolved along CB of the conductor. In this way, heat is transferred due to the current flow in the direction of the current. It is called positive Thomson effect.

Similar effect is observed in metals like silver, zinc, and cadmium. When the copper bar is replaced by an iron bar, heat is evolved along CA and absorbed along BC. Thus heat is transferred due to the current flow in the direction opposite to the direction of current. It is called negative. Similar effect is observed in metals like platinum, nickel, cobalt, and mercury.

Question 39.
A resistor is made by joining two wires of the same material. The radii of two wires are 1 mm and 3 mm white their lengths are 3 cm and 5 cm respectively. A battery of emf 16 V and negligible resistance is connected across the resistor.
Calculate the potential difference across the shorter wire.

Answer:

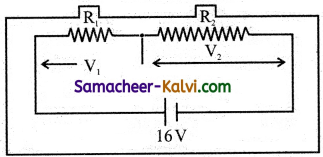
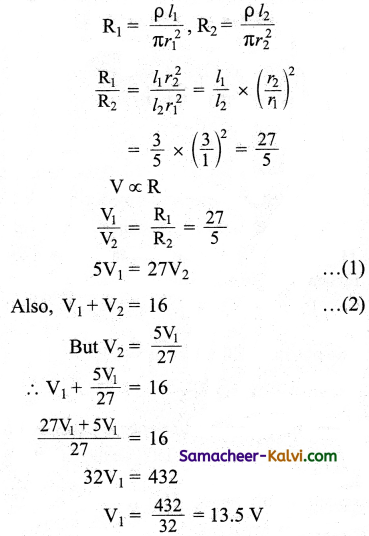
∴ Potential difference across shorter wire = 13.5 V

Question 40.
A Copper wire is stretched to make 0.1 % longer. What is the percentage change in its resistance?
Answer:
Resistance R = \(\frac{\rho l}{\mathrm{~A}}\) ………….(1)

ρ – Specific resistance
Let V be the volume

A = \(\frac{\mathrm{V}}{l}\) …………….(2)

Sub (2) in (1) we get,

R = \(\frac{\rho l^{2}}{\mathrm{~V}}\)

Change in resistance is given by

∴ \(\frac{\Delta \mathrm{R}}{\mathrm{R}}=\frac{2 \Delta l}{100}\)

Here ρ and V are constants.

∴ \(\frac{\Delta \mathrm{R}}{\mathrm{R}}\) × 100 = \(\frac{2 \Delta l}{l}\) × 100

= 2 × \(\frac{1}{4}\) × 100 = 0.2

Percentage change in resistance = 0.2.

Question 41.
What is the drift velocity of an electron in a copper conductor having area 10 × 10^-6 m², carrying a current of 2A. Assume that there are 10 × 10²⁸ electrons/ m³.
Answer:
Area = 10 × 10^-6 m²;
Current = 2 A;
Number of electrons / m³ = 10 × 10²⁸

Drift velocity
v_d = \(\frac{\mathrm{I}}{n \mathrm{~A} e}\)

Drift velocity,
v_d = \(\frac{2}{10 \times 10^{28} \times 10 \times 10^{-6} \times 1.6 \times 10^{-19}}\)

= \(\frac{2}{1.6 \times 10^{5}}\) = 1.25 × 10 5 ms^-1

Dirft velocity = 1.25 × 10 5 ms^-1

Question 42.
Two wires of same material and length have resistances 5 v and 10 Ω respectively. Find the ratio of radii of the two wires.
Answer:
Resistance of first wire R₁ = 5 Ω;
Radius of first wire = r₁
Resistance of second wire R₂ = 10 Ω;
Radius of second wire = r₂
Length of the wires = l;
Specific resistance of the material of the wires = ρ

Question 43.
The resistance of a field coil measures 50 Ω at 20°C and 65 Ω at 70°C. Find the temperature coefficient of resistance.
Answer:
R₂₀ = 50 Ω; 70°C; RTO = 65 Ω; α = ?
R_t = R₀(1 + αt)
R₂₀ = Ro (1 + α20)
50 = R₀(1 + α20) ………….(1)
R₇₀ = R₀(1 + α70)
65 = R₀(1 + α70] ………….(2)
Dividing (2) by (1)

\(\frac{65}{50}=\frac{1+70 \alpha}{1+20 \alpha}\)

65 + 1300 α = 50 + 3500 α
2200 α = 15
α = \(\frac{0.0068}{{ }^{\circ} \mathrm{C}}\)
= 0.0068 / °C

Question 44.
A wire has resistance of 2.0 Ω at 25°C and 2.50 at 100°C. Calculate the temperature coefficient of resistance of the wire.
Answer:
R_t = R₀ (1 + αt)
When t = 25°C R_t = 2.0 Ω
∴ 2.0 = R₀ (1 + 25α) ……..(1)
When t = 100°C R₁₀₀ = 2.5
∴ 2.5 = R₀(1 + 100 α) …(2)
\(\frac{(1)}{(2)} \Rightarrow \frac{2.5}{2.0}=\frac{1+100 \alpha}{1+25 \alpha}\)
∴ 2.5(1 + 25 α) = 2(1 + 100 α)
2.5 + 62.5 α = 2 + 200 α
2.5 – 2 = 2o0 α = 62.5 α
∴ 137.5 α = 0.5
α = \(\frac{0.5}{137.5}\)
α = 0.003636 / °C

Question 45.
A 10 Ω resistance is connected in series with a cell of emf 10 V. A voltmeter is connected in parallel to a cell, and it reads 9.9 V. Find internal resistance of the cell.
Answer:
R = 10 Ω;
E = 10 V;
V = 9.9 V;
r = ?

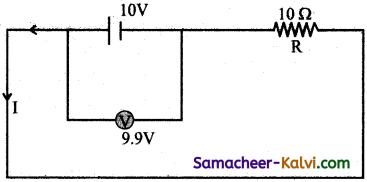
r = \(\left(\frac{E-V}{V}\right) R\)

= \(\left(\frac{10-9.9}{9.9}\right) \times 10\) = 0.101 Ω.

Question 46.
In the given circuit, what is the total resistance and current supplied by the battery.
Answer:
The value of the resistances are
R₁ = 2 Ω; R₂ = 3 Ω; R₃ = 3 Ω; R₄ = 3 Ω
The effective resistance of the resistances R₂, R₃ and R₄ that are connected in parallel.

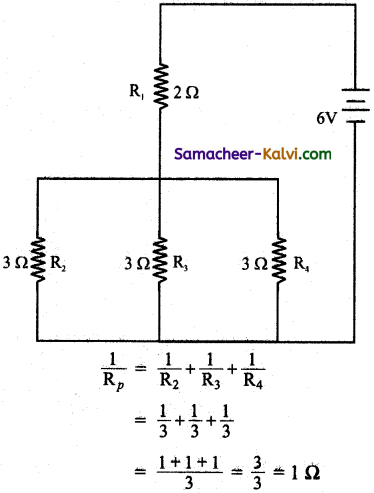
∴ R_p = 1 Ω
The effective resistance of the resistances R₁, R₂, R₃, and R₄ is given by
R_s = 2 + 1 = 3 Ω
Potential difference V = 6V
Resistance R = 3 Ω
∴ Current I = \(\frac{V}{R}=\frac{6}{3}\) = 2 A

Question 47.
Three resistors are connected in series with 10 V supply as shown in the figure. Find the voltage drop across each resistor.

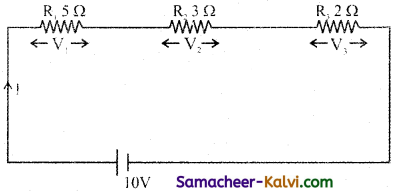
Answer:
R₁ = 5 Ω, R₂ = 3 Ω, R₃ = 2 Ω; V = 10 volt
Effective resistance of series combination,
R_s = R₁ + R₂ + R₃ = R_s = 10 Ω
Current in circuit I = \(\frac{\mathrm{V}}{\mathrm{R}_{s}}=\frac{10}{10}\) = 1A

Voltage drop across R₁, V₁ = IR₁ = 1 × 5 = 5 V
Voltage drop across R₂, V₂ = IR₂ = 1 × 3 = 3 V
Voltage drop across R₃, V₃ = IR₃ = 1 × 2 = 2 V
Voltage drop across each resistor are V₁ = 5 V; V₂ = 3 V; V₃ = 2 V.

Question 47.
Find the effective resistance between A and B in.the given circuit.

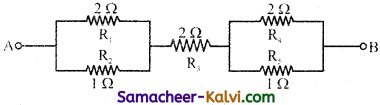
Answer:
The value of resistances are
R₁ = 2 Ω; R₂ = 1 Ω; R₃ = 2 Ω; R₄ = 2 Ω; and R₅ = 1 Ω
The effective resistance of R₁ and R₂ which are connected in. parallel is
\(\frac{1}{\mathbf{R}_{p_{1}}}=\frac{1}{\mathbf{R}_{1}}+\frac{1}{R_{2}}\)

Question 48.
In the given network, calculate the effective resistance between points A and B.

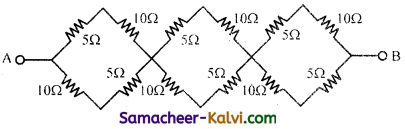
The network has three identical units. The simplified form of one unit is given below:

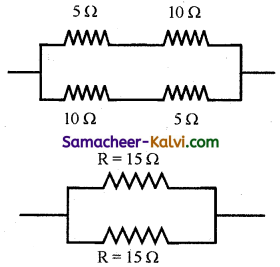
The equivalent resistance of one unit is
\(\frac{1}{\mathrm{R}_{p}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}\)

= \(\frac{1}{15}+\frac{1}{15}\) or R_p = 7.5 Ω

Each unit has a resistance of 7.5 Ω. The total network reduces to

The combined resistance between points A and B is
R= R’ + R’ + R’
(∵ R_s = R₁ + R₂ + R₃)
R = 7.5 + 7.5 + 7.5 = 22.5 d

Question 49.
The resistance of a platinum wire at 0°C is 4 Ω. What will be the resistance of the wire at 100°C if the temperature coefficient of resistance of platinum is 0.0038 /°C.
Answer:
The resistance of a platinum wire at 0° C
R₀ = 4 Ω
Temperature coefficient of resistance \
α = 0.0038 /° C
Resistance at 100°C is
R₁₀₀ = R_t = R₀(1 + αt)
Resistance at 100°C is R₁₀₀ = R_t
R_t = 4 [1 + 0.0038 × 100]
= 4(1 + 0.38)
= 4 × 1.38 = 5.52 Ω
Resistance at 100°C is R₁₀₀ = 5.52 Ω

Question 50.
A cell has a potential difference of 6 V in an open circuit, but it falls to 4 V when a current of 2A is drawn from it. Find the internal resistance of the cell.
Answer:
Initial potential difference E = 6 V
Final potential difference V = 4 V;
Current I = 2A
Internal resistance of the cells r = \(\frac{E-V}{I}\)
Internal resistance of the cell r = \(\frac{6-4}{2}=\frac{2}{2}\) = 1 Ω
Internal resistance of the cell = 1 Ω

Question 51.
Find the voltage drop across 18 Ω resistor in the given circuit.

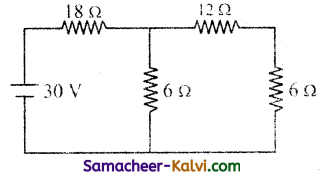
Answer:
The emf of the source = 30 V
The values of resistances are 18 Ω, 12 Ω, 6 Ω and 6 Ω
Two resistances 12 Ω and 6 Ω are connected in series.
R_s = 12 + 6= 18 Ω
R₂ = 6 Ω; R₃ = 18 Ω
The resistances R₂ and R₃ are connected in parallel.
The effective resistance is given by

\(\frac{1}{\mathrm{R}_{p}}=\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}=\frac{1}{6}+\frac{1}{18}\)

= \(\frac{3+1}{18}=\frac{4}{18}=\frac{2}{9}\)

∴ R_p = \(\frac{9}{2}\) Ω
The resistances R₁ and R_p are connected in series.

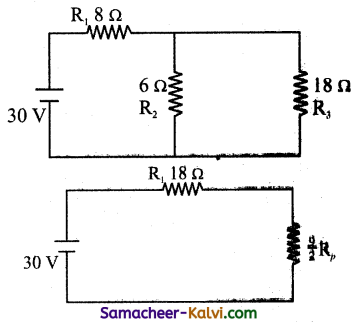
R₁ = 18 Ω; R_p = \(\frac{9}{2}\) Ω

R_s = 18 + \(\frac{9}{2}\) = \(\frac{36+9}{2}=\frac{45}{2}\)

∴ Effective resistance of the circuit = \(\frac{45}{2}\) Ω

Electromotive force V = 30 V
∴ Current I = \(\frac{V}{R}=\frac{30}{\frac{45}{2}}=\frac{30 \times 2}{45}\)

= \(\frac{60}{45}=\frac{4}{3}\) amp.

The voltage drop across 18 Ω is V = IR
V = \(\frac{4}{3}\) × 18 = 24 V

Question 52.
Find the current flowing acrossthree resistors 3 Ω, 5 Ω and 2Ω connected in parallel to a 15 V supply. Also find the effective resistance and tot al current drawn from the supply.
Answer:
R₁ = 3 Ω; R₂ = 5 Ω; R₃ = 2 Ω;
Supply voltage V = 15 volt.
Effective resistance of parallel combination

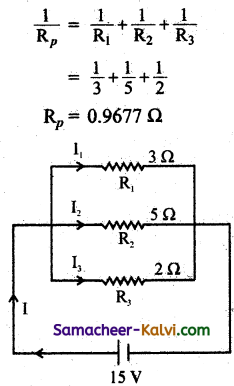
Current through R₁,
I₁ = \(\frac{V}{R_{1}}=\frac{15}{3}\) = 5 A

Current through R₂,
I₂ = \(\frac{V}{R_{2}}=\frac{15}{5}\) = 3 A

Current through R₃,
I₃ = \(\frac{V}{R_{3}}=\frac{15}{2}\) = 7.5 A

Question 53.
Calculate the current I₁, I₂ and I₃ in the given electric circuit.
Answer:

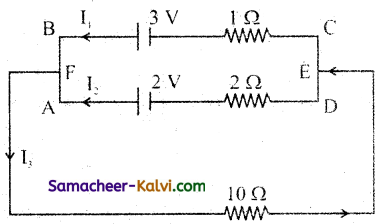
According to Kirchhoff’s first law, at the function F,
I₃ = I₁ + I₂
Applying Kirchhoff’s second law to the closed mesh BFGHECB we get
(I₁ + I₂)10 + I₁ × 1 = 3 ………(1)
Applying Kirchhoff’s second law to the closed mesh AFGHEDA we get
(I₁ + I₂) 10 +I₂ × 2 = 2 ………..(2)
Subtracting Equation (2) from equation (1) we get
I₁ – 2 I₂ = 1 ……..(3)
∴ I₁ = 1 + 2 I₂ …….(4)
Subtracting Equation (4) from equation (2) we get
(1 + 2 I₂ + I₂) × 10 + I₂ × 2 = 2
10 + 30 I₂ + 2 I₂ = 2
32 I₂ = 2 – 10 = – 8
∴ I₂ = – \(\frac{8}{32}\) = – \(\frac{1}{4}\)
I₂ = – 0.25 A
From Equation (4)
I₁ = 1 + 2 I₂ = 1 + 2 (- 0.25)
= 1 – 0.5 = 0.5 A
∴ I₁ = 0.5 A
We know I₃ = I₁ + I₂
= 0.50 + (-0.25)
I₃ = 0.25 A
Current I₁ = 0.5 A;
I₂ = – 0.25 A;
I₃ = 0.25 A.

Question 54.
Find the electric current flowing through the given circuit connected to a supply of 3 V.

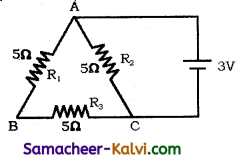
Answer:
R₁ = 5 Ω;
R₂ = 5 Ω;
R₃ = 5 Ω;
Potential difference of supply V = 3V
Current I = \(\frac{V}{R}\)
When resistances are connected in parallel, effective resistance is given by

\(\frac{1}{\mathrm{R}_{p}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}\)

When resistances are connected in series, effective resistance is given by
R_s = R₁ + R₂
= 5 + 5 = 10 Ω

When the resistances R_s and R₃ are connected in parallel, effective resistance is

Question 55.
To balance The Wheatstone’s bridge shown in figure, determine an additional resistance that has to be connected with 3 Ω.

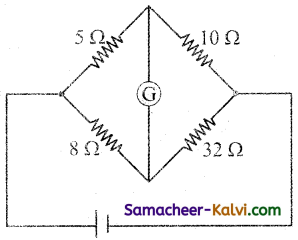
Answer:
P = 5 Ω; Question = 10 Ω; R = 8 Ω; S = 32 Ω;

\(\frac{P}{Q}=\frac{R}{S}\) \(\frac{5}{10}=\frac{8}{32}\)

∴ S = \(\frac{10 \times 8}{5}\) = 16
Hence the value of resistance (s) has to be transformed into 16 Ω as follows:
When another resistance of 32 Ω is connected in parallel with 32 Ω then
\(\frac{1}{\mathbf{R}_{p}}=\frac{1}{32}+\frac{1}{32}\)

= \(\frac{1+1}{32}=\frac{2}{32}\)

∴ R_p = \(\frac{32}{2}\) = 16 Ω
The wheatstone bridge can be balanced by connecting a resistance of 32 Ω is to be connected in parallel with it. The circuit is transformed into P = 5 Ω; Question = 10 Ω.

Question 56.
With an unknown resistance the balancing length obtained in a metre bridge is 20 cm. When 6 Question resistance is connected in series with the unknown resistance., the balancing length changes to 50cm. Calculate the unknown resistance.
Answer:
Balancing lengths for unknown resistance are
l₁ = 20 cm = 2 × 10^-2 m;
l₂ = 100 – 20 = 80 cm = 80 × 10^-2m.
When unknown resistance is connected in series with 6 Ω the balancing lengths are
l₁ = 50 × 10^-2 m;
l₂ = 50 × 10^-2 m
\(\frac{\mathbf{P}}{\mathrm{Q}}=\frac{l_{1}}{l_{2}}\)
Let the unknown resistance be P Ω
P = Question × \(\frac{20}{80}\) …………..(1)
P + 6 = Question × \(\frac{50}{50}\) = Question …………(2)
By dividing equation (2) by equation (1) we get
\(\frac{P+6}{P}=\frac{Q}{Q} \times \frac{80}{20}\) = 4
P + 6 = 4P
∴ 6 = 4P – P = 3P
∴ P = \(\frac{6}{3}\) = 2 Ω
∴ The value of unknown resistance = 2 Ω

Question 57.
In the given circuit, find the current through each branch of the circuit and the potential drop across the 10Question resistor.

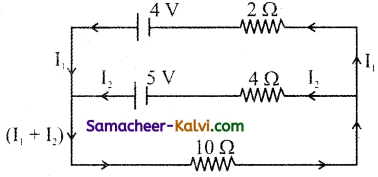
Answer:
Resistance R₁ = 2 Ω;
R₂ = 4 Ω
R₃ = 10 Ω
Electromotive forces E₁ = 4 V and E₁ = 5 V
Application of Kirchhoff’s second law to the closed mesh CDEB we get
– 4 + I₁ × 2 – I₂ × 4 + 5 = 0
2I₁ – 4I₂ = – 1 ……….(1)
Applying Kirchhoff’s second law to the closed mesh BEFA we get,
– 5 + 4 I₂ + 10 (I₁ + I₂) = 0
– 5 + 4 I₂ + 10 I₁ + 10 I₂ = 0
10 I₁ + 14 I₂ = 5 ………..(2)
Equation (2) —>10 I₁ + 14 I₂ = 5 ………(3)
(1) × 5 => 10 I₁ – 20 I₂ = – 5 ………(4)
(3) + (4) => 34 I₂ = 10
∴ I₂ = \(\frac{10}{34}\)
I₂= 0.2941 A
From equation (1) We get
2 I₁ = – 1 + 4 I₂
= – 1 + 4 (0.2941)
= – 1 + 1.1764 = 0.1764
∴ I₁= \(\frac{0.1764}{2}\)
I₁ = 0.0882 A
I₁ + I₂ = 0.0882 + 0.2941 = 0.3823
Potential drop across 10 Ω resistor is
V = (I₁ + I₂) R
= 0.3823 × 10 = 3.823 V

Question 58.
Find the effective resistance of the given circuit.

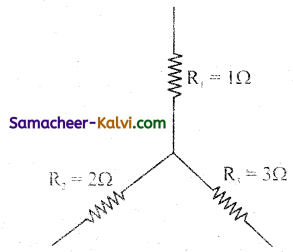
The value of resistances that are connected in series is
R₁ = 1 Ω;
R₂ = 2 Ω;
R₃ = 3 Ω;
R_s = R₁ + R₂ + R₃
The effective resistance is given by
R_s = 1 + 2 + 3 = 6 Ω

Question 59.
Calculate the value of current I min the circuit.

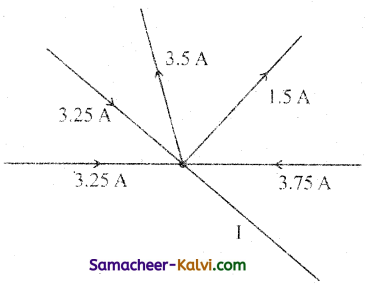
Answer:
Applying Kirchhoff’s First law at the junction we get
3.25 + 3.25 – 3.5 – 1.5 + 3.75 + I = 0
6.5 – 5 + 3.75 + I = 0
∴ I = – 5.25

Question 60.
In a Wheatstone’s bridge a battery of 2 V and a resistance of 2 Ω is used. Find the current through the galvanometer in the unbalanced position of the bridge when P = 1 Ω, Question = 2 Ω, t R = 2 Ω, S = 3 Ω and G = 4 Ω.
Answer:

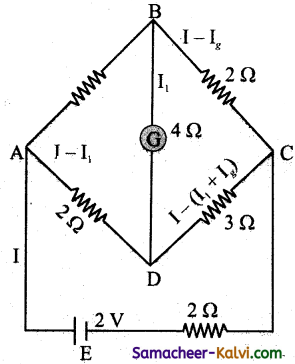
In loop ABDA,
I₁ + 4 I_g – 2(I – I₁) = 0
I₁ + 4 I_g – 2I + 2 I₁ = 0
4 I_g + 3 I₁ – 2I = 0 ……………..(1)
Along the loop BCDB,
2(I₁ – I_g) – 4I_g – 3(I – I₁ + I_g) = 0
2I₁ – 2I_g – 4I_g – 3I + 3I₁ – 3I_g = 0
– 9I_g + 5I₁ – 3I = 0 …………(2)
Along the path ABCEA,
2I + 1I₁ + 2 (I₁ – I_g) = 2
2I + I₁ + 2I₁ – 2I_g = 2
– 2 I_g + 3I₁ + 2I = 2 ……………(3)
4I_g + 3I₁ – 2I = 0 ………….(1)
(3) + 1 ⇒ 2I_g + 6I₁ = 2 …………(4)
(1) × 3 ⇒ 12 I_g + 9I₁ – 6I₁ = 0 ………(5)
(2) × 2 ⇒ – 18 I_g + 10 I₁ – 6I = 0 ………(6)
(5) – (6) ⇒ 30I_g – I₁ = 0 ………….(7)
(7) × 6 ⇒ 180 I_g – 6I₁ = 0 …………(8)
2 I_g + 6 I₁ = 2
(8) + (4) ⇒ 182 I_g = 2
∴ I_g = \(\frac{2}{182}\) = 0.010989 Amp.
Current through the galvanometer = 1.099 × 10^-2 Amp.

Question 61.
The resistance of the four arms P, Q, R and S in a Wheatstone’s bridge are 10 Ω, 30 Ω, 30 Ω and 90 Ω respectively. The emf and interna! resistance of the cell are 7 V and 5 Ω respectively. If the galvanometer resistance is 50 Ω, then calculate the current drawn from the cell.
Answer:

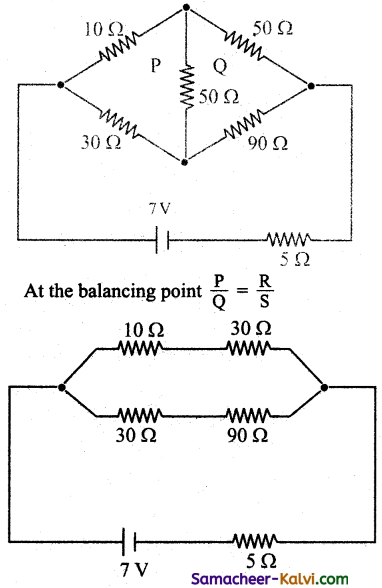
If the bridge is balanced then no current flows through the galvanometer.
R_S1 = 10 + 30 = 40 Ω
R_S2 = 30 + 90 = 120 Ω
\(\frac{1}{\mathrm{R}_{p}}=\frac{1}{40}+\frac{1}{120}=\frac{3+1}{120}\)
= \(\frac{4}{120}\) = \(\frac{1}{30}\)
∴ R_p = 30 Ω
External resistance R = 30 Ω
Current I = \(\frac{E}{R_{p}+R}\)
E = 7 V R_p = 30 Ω R = 5 Ω
∴ I = \(\frac{7}{30+5}=\frac{7}{35}\) = 0.2 A
∴ Current drawn from the cell = 0.2 A

Question 62.
The resistances in the two arms of a metre bridge are 5 Ω and R Ω respectively. When the resistance R is shunted with equal resistance the new balancing point is at 1.6l. Calculate the value of the resistance R.
Answer:

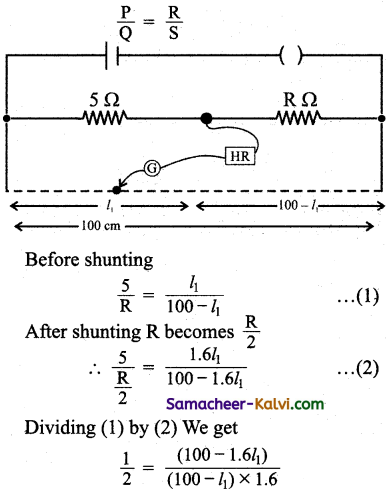
1.6 (100 – l₁) = 2(100 – 1.6l₁)
160 – 1.6 l₁ = 200 – 3.2 l₁
1.6 l₁ = 40
l₁ = \(\frac{40}{1.6}\) = 25 cm.
\(\frac{5}{\mathrm{R}}=\frac{l_{1}}{100-l_{1}}\)

\(\frac{5}{\mathrm{R}}=\frac{25}{100-25}=\frac{25}{75}\)

25 R = 5 × 75
R = \(\frac{5 \times 75}{25}\) = 15 Ω
Resistance R = 15 Ω

Question 63.
In the following circuit, two ceils have negligible resistances. For V_A = 12 V, R₁ = 500 Ω and R = 100 Ω, the galvanometer (G) shows no deflection. Calculate the potential of V_B.
Answer:

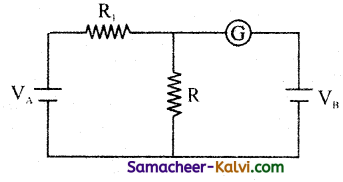
Since there is no deflection in the galvanometer
Current I = \(\frac{\mathrm{V}_{\mathrm{A}}}{\mathrm{R}_{1}+\mathrm{R}}\)
V_A = 12 V
R₁ = 500
R = 100
∴ I = \(\frac{12}{500+100}\)
= \(\frac{12}{600}\) A
∴ Potential of V_B = IR
R = 100 Ω
∴ V_B = \(\frac{12}{600}\)
∴ V_B = 2 V

Question 64.
If the power dissipated in 9 Ω resistor in the given circuit is 36 W, then calculate the potential difference across the 2Ω resistor.

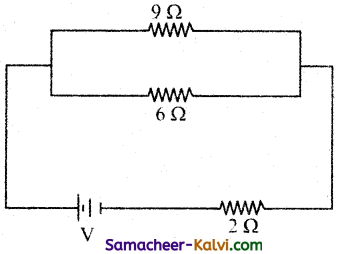
Answer:
Current through 9 Ω resistor is given by
P = I²R
I₁² = \(\frac{36}{9}\) = 4
∴ I₁ = 2 A
Since 9 Ω and 6 Ω are in parallel connection
9 ₁ = 6 I₁
∴ I₂ = \(\frac{9}{6}\) × I₁
I₁ = 2 A
∴ I₁ = \(\frac{9}{6}\) × 2 = 3 A
∴ I = I₁ + I₂ = 2 + 3 = 5 A
∴ Potential difference across 2 Ω resistors is 5 × 2 = 10 V.

Question 65.
An electric iron has a resistance of 80 Ω and is connected to a source of 200 V. If it is used for two hours then Calculate the electrical energy spent.
Answer:
Resistance R= 80 Ω
Potential difference V = 200 V
∴ Power = \(\frac{\mathrm{V}^{2}}{\mathrm{R}}\)
= \(\frac{200 \times 200}{80}\)
P = 500 W
∴ Time t = 2 hour
∴ Electrical energy E = P × t
E = 500 × 2 = 1000 W = 1 kW
∴ Electrical energy spent = 1 kW

Question 66.
Sixteen cells each of emf 3 V are connected in series and kept in a box- External the combination shows an emf of 12 V. Calculate the number of cells reversed in the connection.
Answer:
Number of cells x = 16
emf of each cell E = 3 V
Total emf = nE = 16 × 3 = 48 V
Let the number of cells in reversed direction be n
Total emf -2nE = Effective emf
48 -2n × 3 = 12 V
-6 n = 12 – 48 = -36
Number of cells = \(\frac{-36}{-6}\) = 6
Number of cells reversed in the connection is n = 6

Question 67.
Calculate the value of current I in the following figure at the junction A.

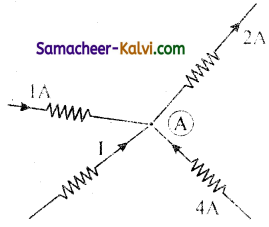
Answer:
Applying Kirchhoff’s current law (I law) we get
1 – 2 + 4 + I = 0
3 + I = 0
∴ I = -3 A
∴ The current flows away from the junction I = – 3 A.

Question 68.
A battery of emf 12 V and internal resistance 2 Ohm is connected to a resistor. The current flowing in the circuit is 0.5 A.
When the circuit is closed. What is the value of Terminal voltage of the battery?
Answer:
emf E = 12 V
Internal resistance r = 2 Ω
Current I = 0.5 V
Terminal voltage of the battery is given by
V=E – Ir
= 12 – 0.5 × 2 = 12 – 1 = 11 V
∴ Terminal Voltage = 11 V

Multiple Choice Questions:

Question 1.
When current I flows through a wire, drift velocity of the electrons is v. When a current 21 flows through another wire of the same material having double the length and area of cross-section, the drift velocity of the electron will be:
(a) 2 v
(b) \(\frac{v}{2}\)
(c) v
(d) \(\frac{v}{4}\)
Answer:
(c) v

Question 2.
A wire of resistance 4 Ω is stretched to twice its original length. The resistance of the stretched wire would be:
(a) 8 Ω
(b) 16 Ω
(c) 2 Ω
(d) 4 Ω
Answer:
(b) 16 Ω
Hint:
R = \(\frac{\rho^{\prime} l}{A}\) = 4 Ω
Since the volume of the wire remains constant
l A = l’ A’
∴ A’ = \(\frac{l \mathrm{~A}}{l}\)

Question 3.
If the length of a wire is doubled and its area is also doubled then its resistance will:
(a) become halved
(b) become two times
(c) become four times
(d) remain unchanged
Answer:
(d) remain unchanged

Question 4.
Across a metallic conductor of non-uniform cross-section a constant potential difference is applied.
Which one of the following statements is correct?
Along the conductor,
(a) drift velocity remains constant
(b) current remains constant
(c) electric field remains constant
(d) current density remains constant
Answer:
(b) current remains constant

Question 5.
Match the following quantities given in column I and II.

Column I	Column II
(i) Current	(A) mho m-1
(ii) Resistance	(B) Volt
(Hi) Potential difference	(C) mho
(iv) Conductivity	(D) ohm
	(E) ampere

(a) (i) – (E); (ii) – (A); (iii) – (B); (iv) – (C)
(b) (i) – (D); (ii) – (B); (iii) – (C); (iv) – (A)
(c) (i) – (A); (ii) – (B); (iii) – (C); (iv) – (D)
(d) (i) – (E); (ii) – (D); (iii) – (B); (iv) – (A)
Answer:
(d) (i) – (E); (ii) – (D); (iii) – (B); (iv) – (A)

Question 6.
According to Faraday’s law of electrolysis, when a current is passed, the mass of ions deposited at the cathode is independent of:
(a) current
(b) charge
(e) time
(d) resistance
Answer:
(d) resistance

Question 7.
The chance of collision of electron on the atom depends on:
(a) length only
(b) radius only
(c) both length and radius
(d) neither the length nor the radius
Answer:
(c) both length and radius

Question 8.
The specific resistance of the material of a conductor of length 3m area of cross-section 0.2 mm2 having a resistance of 2 ohm is:
(a) 1.6 × 10^-8 mho m^-1
(b) 7.5 × 10^-8 mho m^-1
(c) 1.33 × 10^-7 mho m^-1
(d) 1.5 × 10^-8 mho m^-1
Answer:
(b) 7.5 × 10^-8 mho m^-1

Question 9.
Resistance of a metal wire of length 10cm is 2 OE if the wire is stretched uniformly to 50 cm, the resistance is:
(a) 25 Ω
(b) 10 Ω
(c) 5 Ω
(d) 50 Ω
Answer:
(d) 50 Ω

Question 10.
The brown ring at one end of a carbon resistor indicates a tolerance of:
(a) 1 %
(b) 2 %
(c) 5 %
(d) 10 %
Answer:
(a) 1 %

Question 11.
The material through which electric charge can flow easily is:
(a) quartz
(b) mica
(c) germanium
(d) copper
Answer:
(d) copper

Question 12.
The unit of conductivity is:
(a) mho
(b) ohm
(e) ohm-m
(d) mho-m^-1
Answer:
(d) mho-m^-1

Question 13.
The colour code on a carbon resistor is red- red-black. The resistance of the resistor is:
(a) 2.2 Ω
(b) 22 Ω
(c) 220 Ω
(d) 2.2 kΩ
Answer:
(b) 22 Ω

Question 14.
The unit of resistivity is:
(a) ohm metre
(b) (ohm metre)^-1
(c) ohm/metre
(d) mho metre^-1
Answer:
(a) ohm metre

Question 15.
The drift velocity does not depend upon:
(a) the magnetic field
(b) mass of the electron
(c) charge of the electron
(d) relaxation time
Answer:
(a) the magnetic field

Question 16.
The specific resistance of a wire will depend on:
(a) its length
(b) its radius
(c) the type of material of the wire
(d) none of the above
Answer:
(c) the type of material of the wire

Question 17.
When η resistor of equal resistance (R) are connected in series, the effective resistance is:
(a) \(\frac{n}{\mathrm{R}}\)

(b) \(\frac{\mathrm{R}}{n}\)

(c) \(\frac{1}{n \mathrm{R}}\)

(d) nR
Answer:
(d) nR

Question 18.
When two 2 Ω resistances are in parallel, the effective resistance is:
(a) 2 Ω
(b) 4 Ω
(c) 1 Ω
(d) 0.5 Ω
Answer:
(c) 1 Ω
Hint:
\(\frac{1}{\mathrm{R}_{p}}=\frac{1}{2}+\frac{1}{2}=\frac{1}{1}\)
R_p = 1 Ω

Question 19.
The current flowing in a conductor is proportional to:
(a) drift velocity
(b) 1 / area of cross-section
(c) 1 /no. of electrons
(d) square of the area of cross-section.
Answer:
(a) drift velocity

Question 20.
If the length of a copper wire has a certain resistance R, then on doubling the length its specific resistance:
(a) will be doubled
(b) will become \(\frac{1}{4}\)th
(c) will become 4 times
(d) will remain the same
Answer:
(d) will remain the same

Question 21.
A charge of 60 C passes through an electric lamp in 2 minutes. Then the current in the lamp is:
(a) 30 A
(b) 1 A
(c) 0.5 A
(d) 5 A
Answer:
(c) 0.5 A

Question 22.
The flow of electrons in a conductor constitutes:
(a) potential
(b) electric current
(c) resistance
(d) charge
Answer:
(b) electric current

Question 23.
Current is _____ quantity.
(a) a vector
(b) a scalar
(c) not a scalar
(d) a physical
Answer:
(b) a scalar

Question 24.
The resistance of a wire on increasing its temperature will ________ with rise in temperature.
(a) increase
(b) decrease
(c) remain same
(d) increase and decrease
Answer:
(a) increase

Question 25.
The current density of a conductor consisting of n electrons moving with drift velocity v_d and having charge of e is given by:
(a) ev_d

(b) \(\frac{n e v_{d}}{\tau}\)

(c) nev_d

(d) \(\frac{e v_{d}}{n}\)
Answer:
(c) nev_d

Question 26.
The unit of mobility of free electron is:
(a) m² Vs
(b) m² V^-1 s^-1
(c) m² Vs^-1
(d) Vm² s^-1
Answer:
(b) m² V^-1 s^-1

Question 27.
An electric bulb is rated as 220-100W. If the rated value drops by 2.5 % then the percentage of drop in power will be:
(a) 10 %
(b) 5 %
(c) 20 %
(d) 2.5 %
Answer:
(b) 5 %
Hint:

Question 28.
Which of the following pair of expressions for drift velocity v_d is correct?

(a) v_d = \(\frac{e \mathrm{E}}{m} \tau\) and v_d = \(\frac{I}{n A e}\)

(b) v_d = \(\frac{e \mathrm{E}}{m} \tau\) and v_d = IR

(c) v_d = \(\frac{-e \mathrm{E}}{m} \tau\) and v_d = \(\frac{\mathrm{J}}{n \mathrm{~A} e}\)

(d) v_d = \([latex]\frac{-e^{2} E}{m}\)[/latex] and v_d = \(\frac{\mathrm{I}}{n^{2} \mathrm{~A} e}\)

Answer:
(a) v_d = \(\frac{e \mathrm{E}}{m} \tau\) and v_d = \(\frac{I}{n A e}\)

Question 29.
Three conductors draw currents Of 1 A, 2 A and 4 A respectively, when they are connected in series across the same battery, the Current drawn will be:
(a) \(\frac{3}{7}\) A

(b) \(\frac{5}{7}\) A

(c) \(\frac{2}{7}\) A

(d) \(\frac{4}{7}\) A

Answer:
(d) \(\frac{4}{7}\) A
Hint:

Question 30.
For which of the following dependences, of drift velocity vd on electric field E, is ohm’s law obeyed?
(a) v_d ∝ E²
(b) v_d ∝ √E
(c) v_d ∝ E
(d) v_d = constant
Answer:
(c) v_d ∝ E

Question 31.
The relationship between Current density J, conductivity a and Electric field intensity E is:
(a) J = σ² E
(b) J = σ
(c) J = σE
(d) J = \(\frac{E}{\sigma}\)
Answer:
(c) J = σE

Question 32.
The specific resistance of a wire:
(a) varies with its mass
(b) varies with its area
(c) varies with its length
(d) is independent of mass, area and length of the wire.
Answer:
(d) is independent of mass, area and length of the wire.

Question 33.
Select the incorrect statement from the following statement:
(a) A wire carrying current stays electrically neutral.
(b) A high resistance volt meter is used to measure the emf of a cell.
(c) A 6000 V power Supply must have very high internal resistance.
(d) A 6V power supply must have very low internal resistance.
Answer:
(d) A 6V power supply must have very low internal resistance.

Question 34.
Ohm’s law does not hold good for:
(I) current flowing through a diode valve.
(II) current flowing through a triode valve.
(III) current flowing through a NPN Transistor.
(IV) current flowing through a PN junction diode

Which two of the above are correct?
(a) (I) and (II)
(b) (I) and (III)
(c) (III) and (IV)
(d) (II) and (III)
Answer:
(b) (I) and (III)

Question 35.
Select the incorrect statement from the following statement is:
(a) When cells are connected in series external resistance is greater than internal resistance.
(b) When cells are connected in parallel, external resistance is less than internal resistance.
(c) If n identical cells are connected in parallel, emfis E / n and internal resistance is r / n
(d If n identical cells are connected in series, emfis nE and internal resistance is nr.
Answer:
(c) If n identical cells are connected in parallel, emfis E / n and internal resistance is r / n

Question 36.
Which one of the following pairs of quantities remain constant when a steady current flows through a metallic conductors of non-uniform cross-section:
(a) drift speed and current
(b) electric field and current
(c) resistivity and current
(d) resistivity and resistance
Answer:
(b) electric field and current

Question 37.
Which one of the following pairs of quantities is correct for the specific resistance of a wire?
(a) material and length
(b) material and temperature
(c) length and temperature
(d) area and temperature
Answer:
(b) material and temperature

Question 38.
Match the following quantities given in | column I and Column II:

(a) (i) – (B); (ii) – (E); (iii) – (D); (iv) – (A)
(b) (i) – (C); (ii) – (D); (iii) – (B); (iv) – (F)
(c) (i) – (A); (ii) – (D); (iii) – (F); (iv) – (E)
(d) (i) – (F); (ii) – (D); (iii) – (E); (iv) – (A)
Answer:
(d) (i) – (F); (ii) – (D); (iii) – (E); (iv) – (A)

Question 39.
Superconductors are used in:
(a) power generators
(b) computers
(c) launching satellites
(d) all the above
Answer:
(d) all the above

Question 40.
The temperature at which the material changes from normal conductor to a super conductor is called:
(a) absolute temperature
(b) transition temperature
(c) normal temperature
(d) superconducting temperature
Answer:
(b) transition temperature

Question 41.
The temperature at which the resistance of mercury becomes zero is:
(a) 0 K
(b) 0° C
(c) 4.2 K
(d) 4.2 K
Answer:
(c) 4.2 K

Question 42.
The silver ring on the resistor represents ………. tolerance.
(a) 20 %
(b) 10 %
(c) 5 %
(d) 1 %
Answer:
(b) 10 %

Question 43.
For a resistor, the gold coloured ring represents ______ tolerance of it.
(a) 10 %
(b) 5 %
(c) 2 %
(d) 1 %
Answer:
(b) 5 %

Question 44.
1 % tolerance of a resistor is represented by _______ ring drawn on it.
(a) silver
(b) gold
(c) red
(d) brown
Answer:
(d) brown

Question 45.
On the resistor if there is no coloured ring at its end then the tolerance is:
(a) 10 %
(b) 5 %
(c) 20 %
(d) 2 %
Answer:
(c) 20 %

Question 46.
At the transition temperature, the conductivity becomes:
(a) zero
(b) infinity
(c) finite
(d) half of its initial value
Answer:
(b) infinity

Question 47.
The colours of a carbon resistor is yellow, violet and orange. What is the value of the resistor?
(a) 33 kΩ
(b) 4.7 kΩ
(c) 47 kΩ
(d) 22 kΩ
Answer:
(c) 47 kΩ

Question 48.
If a charge of 60 C passes through an electrical equipment in 4 minutes, then the current flowing through it is:
(a) 0.5 A
(b) 0.25 A
(c) 1 A
(d) 2 A
Answer:
(b) 0.25 A

Question 49.
The conductivity of a conductor depends on the _________ of the conductor.
(a) length
(b) material
(c) resistance
(d) area of cross-section
Answer:
(b) material

Question 50.
The resistance of a:
(a) thick conductor is less than that of a thin conductor
(b) thin conductor is less than that of a thick conductor.
(c) short conductor is more than that of a long conductor.
(d) both (a) and (c)
Answer:
(a) thick conductor is less than that of a thin conductor

Question 51.
If a wire of resistance R is stretched to twice its original length, the new resistance of the
wire will be:
(a) \(\frac{\mathrm{R}}{2}\)
(b) 2R
(c) 4R
(d) \(\frac{\mathrm{R}}{4}\)
Answer:
(c) 4R

Question 52.
The temperature coefficient of resistance of alloys is:
(a) positive and small
(b) negative and small
(c) positive and large
(b) negative and large
Answer:
(a) positive and small

Question 53.
The temperature coefficient of manganin is:
(a) small and positive
(b) small and negative
(c) large and positive
(d) large and negative
Answer:
(a) small and positive

Question 54.
The current drawn by 1.5 kW operated at 220 V water heater is:
(a) 6.9 A
(b) 14.6A
(c) 15 A
(d) 6.82 A
Answer:
(d) 6.82 A
Hint:

Question 55.
If two resistors of resistance 3 Ω and 1 Ω are connected in parallel, then the effective i resistance of the system is:
(a) \(\frac{2}{3}\) Ω
(b) .75 Ω
(c) 4 Ω
(d) 5.1 Ω
Answer:
(b) .75 Ω
Hint:
\(\frac{1}{R_{p}}=\frac{1}{3}+\frac{1}{1}=\frac{4}{3}\)

∴ R_p = \(\frac{3}{4}\) = 0.75 Ω

Question 56.
If R₁ and R₂ are resistances of a given coil at temperatures t₁ and t₂, then temperature coefficient of resistance of the material is:
(a) \(\frac{R_{1}-R_{2}}{R_{1} T_{2}-R_{2} T_{1}}\)

(b) \(\frac{R_{2}-R_{1}}{R_{1} T_{2}-R_{2} T_{1}}\)

(c) \(\frac{\mathrm{R}_{2}-\mathbf{R}_{1}}{\mathbf{R}_{2} \mathrm{~T}_{1}-\mathrm{R}_{1} \mathrm{~T}_{2}}\)

(d) \(\frac{R_{1}-R_{2}}{R_{2} T_{1}-R_{1} T_{2}}\)

Answer:
(b) \(\frac{R_{2}-R_{1}}{R_{1} T_{2}-R_{2} T_{1}}\)

Question 57.
Kirchhoffs second law is the consequence of conservation of:
(a) charges
(b) current
(c) energy
(d) potential
Answer:
(c) energy

Question 58.
Kirchhoff’s first law is the consequence of conservation of:
(a) current
(b) potential
(c) charges
(d) resistance
Answer:
(b) potential

Question 59.
According to the principle of potentiometer, the emf of the cell is:
(a) inversely proportional to its balancing length
(b) directly proportional to its balancing length
(c) directly proportional to its resistance
(d) inversely proportional to its resistance
Answer:
(b) directly proportional to its balancing length

Question 60.
If the strength of current flows through a resistor is I having resistance R and potential difference between its ends is V then the power dissipated is:
(a) \(\frac{\mathrm{I}}{\mathrm{V}}\)
(b) IR
(c) \(\frac{\mathrm{I}}{\mathrm{V}}\)
(d) VI
Answer:
(d) VI

Question 61.
The energy equivalence of 1 kWh is:
(a) 3.6 × 10⁵ J
(b) 36 × 10⁵ J
(c) 0.36 × 10⁴4 J
(d) 36 × 10⁶ J
Answer:
(b) 36 × 10⁵ J

Question 62.
The ratio of the emf of two cells when their balancing lengths on a potentiometer are 614.8 cm and 824.4 cm respectively is:
(a) 1.7456
(b) 1.313 J
(c) 0.7456
(d) .8456
Answer:
(c) 0.7456

Question 63.
The resistances in cyclic order of the four arms of Wheatstone’s network at balance is:
(a) 8, 6, 16, 12
(b) 8, 6, 12, 16
(c) 8, 12, 6, 16
(d) 8, 16, 6, 12
Answer:
(b) 8, 6, 12, 16

Question 64.
Two copper wires of length lm and 9m have equal resistances. Then their diameters are in the ratio:
(a) 3 : 1
(b) 9 : 1
(c) 1 : 9
(d 1 : 3
Answer:
(d) 1 : 3

Question 65.
At transition temperature, the resistance of a super conductor:
(a) increases slowly
(b) decreases slowly
(c) increases rapidly
(d) drops to zero
Ans :
(d) drops to zero

Question 66.
Assertion:
The drift speed of electrons in metals is of the order of few mm s and charge of an electron is very small ; (1.6 × 10^-19 C). Yet a large amount of current is obtained.
Reason:
At room temperature, the thermal speed of electron is very high (10⁷ times the drift speed).
Which one of the following statements is j correct?
(a) Both assertion and reason are true and reason explains assertion correctly.
(b) Both assertion and reason are true and reason does not explains assertion correctly.
(c) Assertion is true and reason is false,
(d) Assertion is false and reason is true.
Answer:
(b) Both assertion and reason are true and reason does not explains assertion correctly.
Hint:
Current depends on
(i) Charge
(ii) drift speed
(iii) area and
(iv) no. of free electrons per unit volume of a metal.

Question 67.
Assertion:
In a meter bridge experiment, the balancing length AC corresponding to null deflection of the galvanometer is x.
If the radius of the wire is doubled then the balanced length becomes 4x.
Reason:
The resistance of a wire is inversely proportional to the square of its radius.
Which one of the following statement is correct?
(a) Both assertion and reason are true and reason explains assertion correctly.
(b) Both assertion and reason are true and reasons does not explain assertion correctly.
(c) Assertion is true and reason is false.
(d) Assertion is false and reason is true.
Answer:
(d) Assertion is false and reason is true.
Hint:
If the radius, is doubled the ratio of resistance will remain unchanged.
But, \(\frac{\mathbf{R}_{1}}{\mathrm{R}_{2}}=\frac{l_{1}}{l_{2}}\) = constant
Hence the balancing length will remain same.

Question 68.
Choose the odd man out from the following:
(a) Silver
(b) Mercury
(c) Zinc
(d) Cadmium
Answer:
(b) Mercury
Hint:
Negative Thomson effect is observed only in mercury.

Question 69.
Choose die odd man out.
In which one of die following negative Thomson effect is not observed.
(a) Mercury
(b) Platinum
(c) Nickel
(d) Cadmium
Answer:
(d) Cadmium

Question 70.

Match the following:

Column I	Column II
(i) Positive Thomson effect	(A) Cu – Fe thermocouple.
(ii) Negative Thomson effect	(B) Iron
(iii) Zero Thomson effect	(C) Copper
(iv) Peltier effect	(D) Mercury
	(E) Zinc
	(F) Lead

(a) (i) – (A); (ii) – (B); (iii) – (D); (iv) – (C)
(b) (i) – (C); (ii) – (E); (iii) – (D); (iv) – (A)
(c) (i) – (B); (ii) – (C); (iii) – (D); (iv) – (F)
(d) (i) – (E); (ii) – (D); (iii) – (F); (iv) – (A)
Answer:
(d) (i) – (E); (ii) – (D); (iii) – (F); (iv) – (A)

Question 71.
Assertion:
In the potentionmeter circuit, if the experimental wire AB is not changed then the value of resistor R that is connected to the cell in the primary circuit will be decreased.
Reason:
At the balancing point, the potential difference between A and D to cell C₁ =? emf of E₂ of cell 2.

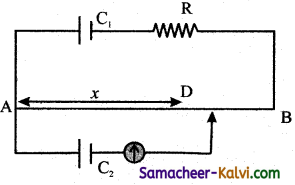
Which one of the following statement is correct:
(a) Both assertion and reason are true and reason explains assertion correctly.
(b) Both assertion and reason are true and reason does not explain correctly.
(c) Assertion is true but reason is false.
(d) Assertion is false but reason is true.
Answer:
(d) Assertion is false but reason is true.
Hint:
If the diameter of wire AB is increased, the resistance will decrease.
So, the potential difference due to cell Question will be decreased.
Hence the null point will be obtained at a higher value of x.

Question 72.
When a resistance of 2 Ohm is connected across the terminals of a cell, the current is 0.5 A. If a resistance of 5 Ohm is connected across the cell then the current is 0.25 A then the emf of the cell is:
(a) 2V
(b) 1.5 V
(c) 1 V
(d) 0.5 V
Answer:
(b) 1.5 V
Hint:
E = I(R + r)
= IR + Ir
∴ r = \(\frac{E}{I}\) – R
∴ \(\frac{E}{0.5}\) – 2 = \(\frac{E}{0.25}\) – 5
∴ E = 1.5 V

Question 73.
5 rows of 10 identical cells, connected in series, send a current I through an external resistance of 20 Ohm.
If the emf and internal resistance of each cell is 1.5 V and 1 Ohm respectively then, value of current (I) is:
(a) 0.25 A
(b) 0.14 A
(c) 0.68 A
(d) 0.75 A
Answer:
(c) 0.68 A
Hint:
Equivalent emf E = 15 V
Equivalent internal resistance r = 2 Ω
I = \(\frac{\dot{E}}{\mathrm{R}+r}\)

= \(\frac{15}{20+2}=\frac{15}{22}\) = 0.68 A

Question 74.
When 115 V is applied across a wire of length 10m and radius 0.3 mm, the current density is 1.4 x 104 A m2. The resistivity of the wire is:
(a) 4.1 × 10⁴ Ωm
(b) 8.2 × 10^-4 Ωm
(c) 16.4 × 10⁴ Ωm
(d) 2.1 × 10⁴ Ωm
Answer:
(b) (b) 8.2 × 10^-4 Ωm
Hint:

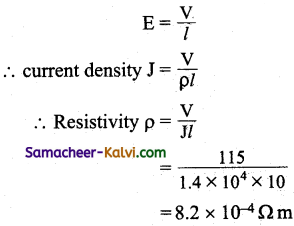
Question 75.
If a wire is stretched to make it 0.1 % longer, the percentage change in its resistance would be:
(a) Zero
(b) 0.1%
(c) 0.2%
(d) 0.4 %
Answer:
(c)
Hint:

TN Board 12th Physics Important Questions