TN State Board 11th Chemistry Important Questions Chapter 2 Quantum Mechanical Model of Atom
Question 1.
Write the values of all the four quantum numbers for all the electrons present in hydrogen and Helium atoms.
Answer:
Hydrogen atom (H):
Electronic configuration = 1s1
The four quantum number of electrons present in a hydrogen atom is
n = 1; l = 0; m = 0; s = +\(\frac{1}{2}\)
The four quantum number of two electrons present in a helium atom is
n = 1; l = 0; m = 0; s = +\(\frac{1}{2}\)
n = l; l = 0; m = 0; s = –\(\frac{1}{2}\)
Question 2.
Write the values of four quantum numbers present in the last electron in an atom having the electronic configuration.
(i) 1s2 2s2 2p1
(ii) 1s2 2s2 2p6 3s2 3p2
Answer:
(i) The last electron is the ‘one’ electron present in ‘p’ sub level.
i.e., n = 2; l = 1; m = -1, 0, or + 1,
s = + \(\frac{1}{2}\) or – \(\frac{1}{2}\)
(ii) If the first electron present in ‘p’ subshell has the following quantum numbers.
n = 3, l = 1, m = -1, 0, (or) + 1, s = + \(\frac{1}{2}\),
the last electron has n = 3, l = 1, m = -1, 0, (or) + 1, s = – \(\frac{1}{2}\).
![]()
Question 3.
How many electrons are present in all subshells (fully filled) with n + l = 5?
Answer:
Subshells with n + l = 5 are 5s, 4p, 3d. Hence electrons present are 2 + 6 + 10 = 18.
Question 4.
What is the angular momentum of an electron in (i) 2s orbital (ii) 4f orbital?
Answer:
Angular momentum of electron in any orbital = \(\sqrt{l(l+1)} \times \frac{h}{2 \pi}\)
(i) for 2s orbital, l = 0
∴ angular momentum = \(\sqrt{0(0+1)} \cdot \frac{h}{2 \pi}\) = 0
(ii) for 4/orbital, l = 3
∴ angular momentum = \(\sqrt{3(3+1)} \cdot \frac{h}{2 \pi}\)
= 2√3 \(\frac{h}{2 \pi}\) = √3 \(\frac{h}{2 \pi}\)
![]()
Question 5.
Why Pauli exclusion principle is called exclusion principle?
Answer:
This is because, according to this principle, if one electron in an atom has same particular values for the four quantum numbers, then all the other electrons in that atom are excluded from having the same set of values.
Question 6.
At what distance is the radial probability maximum for 1s orbital? What is this distance called?
Answer:
0.529 Å, Bohr radius.
Question 7.
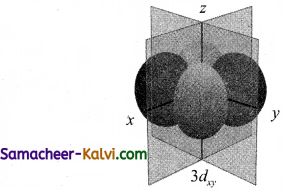
Draw the shapes (boundary surfaces) for the following orbitals.
(i) 2px
(ii) 3dz2
(iii) 3dx2 – y2
Answer:
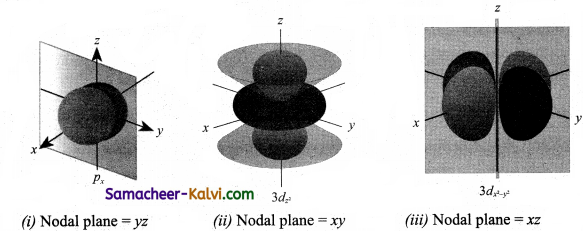
![]()
Question 8.
Bring out the similarities and dissimilarities between a 1s and 2s orbital
Answer:
Similarities:
(i) Both have similar shape.
(ii) Both have same angular momentum =\(\sqrt{l(l+1)} \frac{h}{2 \pi}\)
Dissimilarities:
(i) 1s orbital has no node while 2s orbital has one node.
(ii) Energy of 2s orbital is greater than 1s orbital.
(iii) The size of the 2s orbital is larger than 1s orbital.
Question 9.
How many radial / spherical nodes will be present in 5f orbital?
Answer:
No. of radial nodes = n – l +1 = 5 – 3 – 1 = 1.
![]()
Question 10.
(i) What is the common between dxy and dx2 – y2 orbitals?
(ii) What is the angle between the lobes of the above two orbitals?
Answer:
(i) (a) Both have identical shape consisting of four lobes.
(b) Lobes of dx2 – y2 lie along the x and y axes while those of dxy lie between the axes.
(ii) 45° i..e, the lobes and dxy lie at angle of 45° to the lobes of dx2 – y2.
Question 11.
For each of the following pair of hydrogen orbitals indicate which is higher in energy?
(i) 1s, 2s
(it) 2p, 3p
(iii) 3dxy, 3dyz
(iv) 3s, 3d
(v) 4f, 5s.
Answer:
(i) 2s > 1s
(ii) 3p > 2p
(iii) 3dxy > 3dyz
(iv) 3s = 3d
(v) 5s > 4f
![]()
Question 12.
Which orbital in. each of the following pairs is lower in energy in a many*electron atom?
(i) 2s, 2p
(ii) 3p, 3d
(iii) 3s, 4s
(iv) Ad, 5f
Answer:
(i) 2s < 2p
(ii) 3p < 3d
(iii) 3s < 45
(iv) 4d < 5f
Question 13.
How many electrons in sulphur (z = 16) can have n + l = 3?
Answer:
The electronic configuration of sulphur is
1s2 2s2 2p6 3s2 3p4.
For 1s2, n + l = l + 0 = 1;
For 2p6, n + l = 2 + 1 = 3
2s2, n + l = 2 + 0 = 2;
For 3s2, n + l = 3 + 0 = 3
3p4 n + l = 3 + 1 = 4
Thus n + l = 3 for 2p6 electron and 3s2 electron = 8 electrons.
![]()
Question 14.
The ground state electronic configurations listed below here are incorrect. Explain what stakes have been made in each and correct the electronic configuration.
(i) Al – 1s2 2s2 2p6 3s2 3p1.
(ii) B = 1s2 2s2 2p5
(iii) F = 1s2 2s2 2p5
Answer:
(i) In Al, 2p should be filled before filling 3s, orbital states.
∴ correct electronic configuration is 1s2 2s2 2p6 3s2 2p1
(ii) In B, total electrons = 5. Electronic configuration is 1s2 2s2 2p1
(iii) In F, total electrons = 9. Electronic configuration is 1s2 2s2 2p5
Question 15.
Chromium (Z = 24) and copper (Z = 29), should have the configuration.
Cr = 1s2 2s2 2p6 3s2 3p6 3d4 4s2
Cu = 1s2 2s2 2p6 3s2 3p6 3d9 4s2
But their actual configuration are
Cr – 1s2 2s2 2p6 3s2 3p6 3d5 4s1 and
Cu = 1s2 2s2 2p6 3s2 3p6 3d10 4s1 Explain the reason.
Answer:
The reasons are:
(i) Symmetrical distribution:
3ds5 (half-filled) and 3ds10 (completely filled) one more symmetrical and hence more stable.
(ii) Exchange energy:
Electrons with parallel spins in degenerate orbitals tend to exchange their positions. As a result, energy is released. This energy is called exchange energy. Greater the energy, greater is the stability.
![]()
Question 16.
Give a brief account of the shapes of atomic orbitals.
Answer:
The shape of an atomic orbital is found by finding, the probability (ψ2) of the electron at different points arotmd the nucleus and representing the density of the nucleus. Same orbitals are found to have a region of space where the probability of finding electron is zero. This is called a node.
(i) All ‘s’ orbitals are spherical in shape.
(ii) All ‘p’ orbitals are dumb-bell in shape.
The three ‘p’ orbitals differ in orientation. They lie along the axes and called px, py and pz orbitals.
(iii) All ‘d’ orbitals have clover-leaf shaped with four lobes. Three have lobes between axes and are called dxy, dyz, dxz orbitals. The fourth lobe is along the axes and is called dx2 – y2. The fifth has two lobes along V axis and dough-nut shape in the centre and is called dz2.
Question 17.
Calculate the wavelength of the radiations emitted when an electron in a hydrogen atom undergo transition from 4th energy level to the 2nd energy level.
Answer:
For hydrogen atom
En = \(\frac{-21.8 \times 10^{-19}}{n^{2}}\) J atom (or)
En = \(\frac{-13.6}{n^{2}}\) eV atom-1 (1 eV = 1.6 × 10-9 J)
Energy is emitted when an electron jumps from n = 4 to n = 2 will be given by
∆E = E4 – E2
= 21.8 × 10-19 \(\left[\frac{1}{2^{2}}-\frac{1}{4^{2}}\right]\)
= 21.8 × 10-19 × \(\frac{3}{16}\)
= 10-19 J
= 4.0875 × 10-19 J
The wave length corresponding to this transition is
E = hυ = h\(\frac{c}{\lambda}\) or λ = \(\frac{h c}{E}\)
= \(\frac{\left(6.620 \times 10^{-34} \mathrm{JS}\right) \times\left(3 \times 10^{8} \mathrm{~ms}^{-1}\right)}{4.0875 \times 10^{-19} \mathrm{~J}}\)
= 4.863 × 10-7 m
= 4863 Å or 486.3 nm
![]()
Question 18.
Calculate the wave length of an electron (mass = 9.1 × 10-31 kg) moving with a velocity of 103ms-1 (h = 6.6 × 10-34 kg m2 sec-1).
Answer:
Given m = 9.1 × 10-31 kg;
υ = 103ms-1
h = 6.6 × 10-34 kg m2 sec-1
λ = \(\frac{h}{m v}\)
= \(\frac{6.6 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{sec}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 10^{3} \mathrm{~ms}^{-1}}\)
= 7.25 × 10-7 m
Question 19.
Calculate the de Broglie wave length of an electron that has been accelerated from rest through a potential differences of 1 KV.
Answer:
Energy acquired by the electron (as kinetic energy) after being accelerated by a potential difference of 1 KV i.e., 1000 volts = 1000 eV
= 1000 × 1.602 × 10-19 J
= 1.602 × 10-16 J (1 eV = 1.602 × 10-19 J)
Energy in Joules = charge on the electron in coulombs × potential difference in volts.
i.e., Kinetic Energy (KE) = \(\frac{1}{2}\) mv2
= 1.602 × 10-16 J or \(\frac{1}{2}\) × 9.1 × 10-31 v2
v2 = 3.521 × 1014 or
v = 1.88 × 10-1 ms-1
∴ λ = \(\frac{h}{m v}\)
= \(\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 1.88 \times 10^{-1} \mathrm{~ms}^{-1}}\)
= 3.87 × 10-11 m.
![]()
Question 20.
The kinetic energy of a sub atomic particle is 5.58 × 10-25 J. Calculate the frequency
of the particle wave. (Planck’s constant h = 6.626 × 10-34 kg m2 s-1)
Answer:
KE = \(\frac{1}{12}\) mv2 = 5.85 × 10-25 J
By de Broglie equation,
λ = \(\frac{h}{m v}\)
But λ = \(\frac{v}{\nu}=\frac{v}{\nu}=\frac{h}{m v}\) or
υ = \(\frac{m v^{2}}{h}=\frac{2 \times 5.85 \times 10^{-25} \mathrm{~J}}{6.026 \times 10^{-34} \mathrm{~J}}\) = 1.77 × 109 s-1
Question 21.
A microscope using suitable photons is employed to locate an electron in an atom within a distance of 0.1 Å. What is the uncertainty involved in the measurement of its velocity.
Answer:
Given Ax = 0.1 Å or 0.1 × 10-10 m or 10-11 m
h = 6.626 × 10-34 kg m2 s-1
m = 9.11 × 10-31 kg
According to uncertainty principle,

![]()
Question 22.
If an electron is moving with a velocity 600ms-1 which is accurate upto 0.005 %, then calculate the uncertainty in its position. (h = 6.63 × 10-34 Js. mass of electron = 9.1 × 10-31 kg)
Answer:
Velocity of the electron = 600 ms-1
Uncertainty in velocity = \(\frac{0.005}{100}\) × 600 ms-1 = 0.03 ms-1
= 3 × 10-2 ms-1
Now, (∆x) (m ∆ v)

Question 23.
A golf ball has a mass of 40g and a Speed of 45 m/s. If the speed can be measured within accuracy of 2% calculate the uncertainity in position.
Answer:
Uncertainity in speed = 2 % of 40 ms-1
i.e., ∆v = \(\frac{2}{100}\) × 45 = 0.9 ms-1
Applying imcertainty principle,
∆x (m × ∆v) = \(\frac{h}{4 \pi}\)
∆x = \(\frac{h}{4 \pi \cdot m \cdot \Delta v}\)
= \(\frac{6.626 \times 10^{-34} \mathrm{Kgm}^{2} \mathrm{~s}^{-1}}{4 \times 3.14 \times\left(40 \times 10^{-3} \mathrm{Kg}\right)\left(0.9 \mathrm{~ms}^{-1}\right)}\)
= 1.46 × 10-33 m
![]()
Question 24.
Calculate the kinetic energy of a moving electron which has a wavelength 4.8 pm. (mass of electron = 9.11 × 10-311 kg, h = 6.63 × 10-34 Js)
Answer:

Question 25.
Two particles A and B are in motion. If the wavelength associated with particleA is 5 × 10-8 m, Calculate the wavelength associated with particle B. If its momentum is half of A.
Answer:
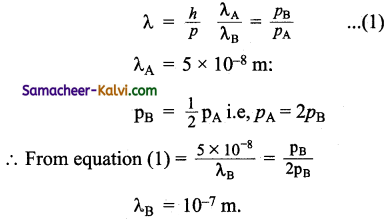
![]()
Question 26.
Light of wavelength 12818Å is emitted when the electron of a hydrogen atom drops from 5th to 3rd orbit. Find the wavelength of a photon emitted when the electron falls from 3rd to 2nd orbit.
Answer:

Choose the correct answer:
Question 1.
The speed of light is 3 × 1o17 nms-1. Which is the closest to the wavelength in nanometer of a quantum of light with frequency of 6 × 1015 s-1?
(a) 10
(b) 25
(c) 50
(d) 75
Answer: (c)
Hint:
υ = \(\frac{c}{\lambda}\)
λ = \(\frac{c}{v}=\frac{3 \times 10^{17} \mathrm{n} \mathrm{ms}^{-1}}{6 \times 10^{15} \mathrm{~s}^{-1}}\) = 50 nm
Question 2.
The velocity of light is 3 × 108 ms-1. The wave length of violet radiation is 400 nm. The wavelength in frequency (Hz) is:
(a) 7.5 × 1014 Hz
(b) 7.5 × 1015 Hz
(c) 7.5 × 1013 Hz
(d) 7.5 × 1016 Hz
Answer: (a)
Hint: Wave length of violet radiation = 400 nm = 400 × 10-9 m.
Frequency (υ) = \(\frac{c}{\lambda}=\frac{3 \times 10^{8} \mathrm{~ms}^{-1}}{400 \times 10^{-9} \mathrm{~m}}\)
= 7.5 × 1014 s-1 = 7.5 × 1014 Hz
![]()
Question 3.
The wave length of the electron emitted when in a hydrogen atom, electron falls from infinity to stationary state 1, would be (Rydbey constant = 1.097 × 107 m-1).
(a) 91 nm
(b) 192 nm
(c) 406nm
(d) 9.1 × 10-8 nm
Answer:(a)
Hint:

Question 4.
The energy associated with the first orbit of He+ ion is:
(a) 8.72 × 10-18 J
(b) 8.78 × 1018 J
(c) 8.78 × 10-17 J
(d) – 8.72 10-17 J
Answer: (a)
Hint:
En = \(\frac{-2.18 \times 10^{-18} \mathrm{Z}^{2}}{n^{2}}\) J/atom
For He+ ion, n = 1, Z = 2
∴ E1 = \(\frac{-2.18 \times 10^{-18} \mathrm{Z}^{2}}{n^{2}}\)
= – 8.72 × 10-18 J
![]()
Question 5.
The radius of the first orbit of He4 ion is:
(a) 0.027 nm
(b) 0.27 nm
(c) 2.7 nm
(d) 0.35 nm
Answer: (a)
Hint:
Radius of hydrogen like species is:
rn = \(\frac{(0.0529) n^{2}}{Z}\) nm
For He+, n = 1, Z = 2
∴ r1 = \(\frac{0.0529 \times 1^{2}}{2}\) = 0.02645 nm. = 0.027 nm
Question 6.
Given that the energy of the first Bohr about is -1312 kJ mol-1, the ionisation energy of hydrogen atom is:
(a) – 1312 kJ
(b) 1312 kJ
(c) 21.8 × 10-20 J
(d) 2.18 × 10-19 J
Answer: (b)
Hint: Ionisation energy is the energy required to remove the electron completely from the atom so as to convert it to a positive ion. This means that it is the enerev absorbed by the electron in the ground state, to jump to n = ∞.
Thus, IE = E∞ – E1 = 0 – (- 1312 kJ) = 1312 kJ mol-1.
Question 7.
The radius of which of the following is same as that of the first Bohr orbit of hydrogen atom?
(a) He+ (n = 2)
(b) Li+2 (n = 2)
(c) Li+2 (n = 3)
(d) Be+3 (n = 2)
Answer: (d)
Hint:
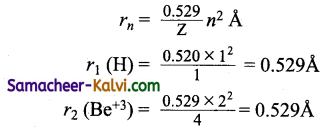
or Bohr theory is applicable to hydrogen and hydrogen like species. Be has electronic configuration 1s2 2s2. If ‘3’ electrons are lost, Be+3 has one electron.
![]()
Question 8.
Calculate the energy in joule corresponding to light of wave length 45 nm, (h = 6.63 × 1034 J, c = 3 × 108 ms-1)
(a) 6.67 × 1015 J
(b) 6.67 × 1011 J
(c) 4.42 × 10-15 J
(d) 4.42 × 10-18 J
Answer: (d)
Hint:
E = \(\frac{h c}{\lambda}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{45 \times 10^{-9}}\)
= 0.442 × 10-17 = 4.42 × 10-18 J.
Question 9.
ψ2 = 0 represents:
(a) a node
(b) an orbital
(c) angular wave function
(d) wave fimction
Answer: (a)
Hint: ψ2 is zero means probability of finding the electron in an orbital in zero, i.e., it represents a node.
Question 10.
If the de Broglie wave length of a particle of mass (m) is 100 times its velocity, then its value in terms of its mass (m) and planck’s constant (h) is:
(a) \(\frac{1}{10}\) \(\sqrt{\frac{m}{h}}\)
(b) 10 \(\sqrt{\frac{h}{m}}\)
(c) \(\frac{1}{10}\) \(\sqrt{\frac{h}{m}}\)
(d) 10 \(\sqrt{\frac{m}{h}}\)
Answer: (b)
Hint: Suppose the velocity (v) = x, then de Broglie wave length = 100 x.
now (λ)= \(\frac{h}{m v}\)
∴ 100 x = \(\frac{h}{m x}\)
(or) x = \(\frac{1}{10}\) \(\sqrt{\frac{h}{m}}\)
Hence λ = 100x (or) 10 \(\sqrt{\frac{h}{m}}\)
![]()
Question 11.
Maximum number of electrons in a subshell of an atom is determined by the following:
(a) 2l + 1
(b) 4l – 2
(c) 2n2
(d) 4l + 2
Answer: (d)
Hint: Number of sub shells = 2l + 1
Maximum number of electrons = 2 (2l+ 1) = 4l + 2 .
Question 12.
For a principle quantum number n = 4, the total number of orbitals having l = 3 is:
(a) 3
(b) 7
(c) 5
(d) 9
Answer: (b)
Hint: When n = 4, l = 0, 1, 2, 3 i.e., 4s, 4p, 4d and 4f subshells.
But l = 3 is for f subshell which has 7 orbitals.
Question 13.
What is the maximum number of electrons that can be associated with the following set of quantum numbers? n = 3, l = 2, m = + 2
(a) 1
(b) 2
(c) 3
(d) 4
Answer: (b)
Hint: n = 3, l = 2, represents ‘3d’ subshell.
It has five orbitals with magnetic quantum number -2, -1, 0, +1, +2. The value m = +2 represents one of the five ‘d’orbitals, i.e., any orbital can have a maximum of 2 electrons.
![]()
Question 14.
The orbital angular momentum of a ‘p’ electron is given as:
(a) \(\sqrt{\frac{3}{2}} \frac{h}{\pi}\)
(b) \(\sqrt{6} \frac{h}{2 \pi}\)
(c) \(\frac{h}{\sqrt{2} \pi}\)
(d) \(\sqrt{3} \frac{h}{2 \pi}\)
Answer: (c)
Hint: For a ‘p’ orbital, l = 1.
Orbital angular momentum = 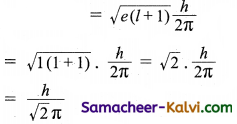
Question 15.
Which of the following orbitals will have zero probability of finding electrons in the yz plane?
(a) Px
(b) py
(c) Pz
(d) dyz
Answer: (a)
Hint: px orbital lies along the ‘x’ axis. Hence the probability of finding an electron is zero in the yz plane.
Question 16.
The maximum probability of finding electrons in dxy orbital is: ,
(a) along the x axis
(b) along they axis
(c) at an angle 45° from the x axis and y-axis
(d) at an angle 90° from the x axis and y-axis
Answer: (c)
Hint: The dxy orbital has lobes between x-axis and y-axis i.e., at an angle of 45° from x-axis and y- axis.
![]()
Question 17.
The orbital diagram in which both the Pauli’s exclusion principle and Hund’s rule are violated is:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Answer: The correct distribution is (b)
Hint: There are six electrons to be filled in 3 orbitals. According to Pauli exclusion principle and Hund’s rule, the correct order of filling up orbitals are ![]()
Question 18.
Which is the correct order of increasing energy of the listed orbitals in the atom of titanium? (at. no = 22)
(a) 3s, 3p, 3d, 4s
(b) 3s, 3p, 4s, 4d
(c) 3s, 4s, 3p, 3d
(d) 4s, 3s, 3p, 3d
Answer: (b)
Hint: As per (n + l) rule.
Question 19.
If n = 6, the correct sequence of filling of electrons will be:
(a) ns → np (n – 1) d → (n- 2)f
(b) ns → (n – 2) → (n – 1) d → np
(c) ns → (n – 1) d → {n – 2)f → np
(d) ns → (n- 2) f – np → (n – 1) d
Answer: (b)
Hint: The orbitals are 6s, 6p, 5d and 4f. As per (n + l) rule, the order of filling is 6s, 4f, 5d, 6p. i.e., ns, (n – 2)f (n -1 )d, np.
![]()
Question 20.
The electrons identified by the quantum numbers n and l :
(1) n = 4, l = 1
(2) n = 4, l = 0
(3) n = 3, l = 2
(4) n = 3, l = 1 can be placed in the order of increasing energy as:
(a) 1 < 3 < 2 < 4
(b) 3 < 4 < 2 < 1
(c) 4 < 2 < 3 < 1
(d) 2 < 4 < 1 < 3
Answer:
Hint (i) = 4p; (2) = 4s (3) = 3d; (4) = 3p
Question 21.
Principal, azimuthal and magnetic quantum numbers are related to:
(a) size, orientation and shape
(b) size, shape and orientation
(c) shape, size and orientation
(d) none of these
Answer: (b)
Question 22.
The angular momentum of an electron is zero. In which orbital it may be present?
(a) 2s
(b) 2p
(c) 3d
(d) 4f
Answer: (a)
![]()
Question 23.
Which of the following expressions represents the electron probability function?
(a) 4πr dr ψ²
(b) 4πr² dr ψ
(c) 4πr² dr ψ²
(d) 4πr dr ψ
Answer: (d)
Question 24.
Which of the following has the largest wave length, provided all have equal velocity?
(a) carbon di oxide molecule
(b) electron
(c) ammonia molecule
(d) proton
Ans (b)
Hint :
λ = \(\frac{h}{m v}\) or λ α \(\frac{1}{m}\)
Question 25.
The number of planar nodes inan orbital can be determined from the value of:
(a) principal quantum number (n)
(b) azimuthal quantum number (l)
(c) both principal and magnetic quantum number (n, m)
(d) magnetic quantum number (m)
Answer: (b)
![]()
Question 26.
Match the quantum numbers with the information provided by these and choose the correct option out of four options given.
| Column I
(Quantum number) |
Column II (Information provided) |
| (i) Principal Quantum number | (A) Orientation of the orbital |
| (ii) Azimuthal Quantum number | (B) Energy and size of the orbital |
| (iii) Magnetic Quantum number | (C) Spin of the electron |
| (iv) Spin Quantum number | (D) Shape of orbital |
(a) (i) – (B), (ii) – (D), (iii) – (A), (iv) – (C)
(b) (i) – (D), (ii) – (A), (iii) – (B), (iv) – (C)
(c) (i) – (C), (ii) – (B), (iii) – (A), (iv) – (D)
(d) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)
Answer: (a)
Question 27.
Match the orbitals in Column I with their corresponding radical nodes given in Column II.
| Column I (Orbitals) | Column II (Radial nodes) |
| (i) 3p | (A) 0 |
| (ii) 5d | (B) 1 |
| (iii) 4f | (C) 2 |
| (iv) 4s | (D) 3 |
(a) (i) – (C), (ii) – (B), (iii) – (D), (iv) – (A)
(b) (i) – (A), (ii) – (B), (iii) – (C), (iv) – (D)
(c) (i) – (C), (ii) – (D), (iii) – (A), (iv) – (B)
(d) (i) – (B), (ii) – (C), (iii) – (A), (iv) – (D)
Answer: (d)
Hint:
Number of radial nodes = n – l – 1
![]()
Question 28.
Among the four options given, one is totally irrelevant to the question. Identify that.
The electronic configuration of carbon atom is 1s2 2s2 2px1 2py1. This is in accordance with:
(a) Aufbau principle
(b) Hund’s rule
(c) Pauli exclusion principle
(d) Bohr model of atom
Answer: (d)
Question 29.
Select the odd man out from the following: The dual nature of matter:
(a) is discovered by de Broglie.
(b) is applicable to microscopic particles.
(c) gives the relationship between the ; wavelength of the matter wave and velocity of the particle.
(d) was verified by Schrodinger wave equation.
Answer: (d)
Hint: Wave nature of radiation was verified by Davisson and Germer’s experiment and G.P.Thomson’s experiment. Particle nature was verified by Mulliken oil drop experiment and by photo electric effect.
Question 30.
Which of the following pairs of Statements correctly explains as the basis for quantum mechanical model of atom?
(a) Bohr’s model and Rutherford model.
(b) Bohr’s model and De Broglie concept.
(c) de Broglie concept and Heisenberg uncertainty principle.
(d) Heisenberg’s uncertainty principle and Bohr model.
Answer: (c)
![]()
Question 31.
Which of the following sets of orbitals have the same energy in terms of their quantum numbers.
(a) n =3, l = 2, m = -1, s = +\(\frac{1}{2}\) and n = 4, l = l, m = 0, s = +\(\frac{1}{2}\)
(b) n = 4, l = 2, m = -2, s = –\(\frac{1}{2}\) and n = 4, l = 1, m = 0, s = +\(\frac{1}{2}\)
(c) n = 4, l = 1, m = -1, s = –\(\frac{1}{2}\) and n = 4, l = 2, m = 0, s = +\(\frac{1}{2}\)
(d) n = 3, l = 1, m = 0, s = +\(\frac{1}{2}\) and n = 2, l = 0, m = 0, s = –\(\frac{1}{2}\)
Answer: (a)
Hint: n + l rule
Question 32.
Assertion:
orbitals do not have any spherical node.
Reason :
The number of nodes in ‘p’ orbitals is given by (n – 2) where ‘n’ is the principal quantum number.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer: (a)
Hint: The number of spherical nodes in any orbital is n – l – 1. For ‘p’ orbital n = 2; l = 1.
![]()
Question 33.
Assertion: Fe+3 ion is more stable than Fe+2 ion.
Reason: Fe+3 ion has more number of unpaired electrons than Fe+2 ion.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer: (b)
Hint:
The correct explanation is Fe+3 ion has more number of unpaired electrons than Fe+2 greater the number of unpaired electrons greater is its exchange energy.
Question 34.
Assertion:
The opposite lobes of a ‘p’ orbital have opposite sign whereas opposite lobes of ‘d‘ orbital have the same sign.
Reason :
The opposite lobes of ‘p’ orbitals have opposite charge, whereas the opposite lobes of ‘d‘ orbital has the same charge.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer: (c)
Hint: Correct Statement (Reason):
The (+) and (-) sign represent the sign of the wave function and not the charge.
![]()
Question 35.
Assertion:
The number of radial nodes in 3s and 4p orbitals are not equal.
Reason :
The number of radial nodes depend upon the values of ‘n’ and ‘l’ which are different for 3s and 4p orbitals.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are, true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer: (d)
Hint: Correct Statement (Assertion):
Number of radial nodps in any orbital is
(n – l – 1). Thus, they depend upon the values of ‘n’ and ‘l’ but for 3s, n – l – 1 = 3 – 0 – 1 = 2 and for 4p, n – l – 1 = 4 – 1 – 1 = 2.
Question 36.
Assertion:
Only principal quantum number determines the energy of an electron in an orbital of Na atoms.
Reason : For one electron system, the expression of energy is quite different from that obtained in Bohr’s theory.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer: (d)
Hint: Correct Statement (Assertion):
To find the energy of an electron in an orbital, both principal and Azimuthal quantum number required.
Correct Statement (Reason):
For one electron system, the expression is same as that obtained by Bohr theory.
![]()
Question 37.
Choose the correct statement from among the following:
(a) For 2px orbital, the values of n, l and m are 2, l + 1 respectively.
(b) ‘s’ orbital has directional characteristics.
(c) The maximum number of electrons that can be accommodated in a ‘d’ sub shell is 8.
(d) The orientation of the orbital is given by Azimuthal quantum number.
Answer: (a)
Question 38.
Choose the correct statements from the following sentences:
(a) The 3s, 3p and 3d orbitals in case of hydrogen atom have the same energy (z = 2l).
(b) Scandium is the element which has only one electron in the ‘d’ orbital.
(c) The electronic configuration of Cu+ (z = 29) is 1s2 2s2 2p6 3s2 3p6 3d8 4s2
(d) The energy of 2px, 2py, 2pz is in the order
2Pz > 2py > 2px
Answer: (a)
Question 39.
Choose the incorrect statement from among the following:
(a) The wave nature of electron is proved by Davisson and Germer experiment.
(b) Ĥψ = Eψ is the briefest form of Schrodinger wave equation.
(c) De Broglie’s concept is used in the construction of electron microscope.
(d) The wavelength of a moving particle is directly proportional to its velocity.
Answer: (d)
Hint: λ ∝ \(\frac{h}{m v}\)
i.e., λ is inversely proportional to its velocity (v).
![]()
Question 40.
Choose the incorrect statement from the I following sentences:
(a) According to Bohr theory the transition n = 6 to n = 5 in the hydrogen atom will produce the least energetic photon.
(b) The angular momentum of an electron in ‘d’ orbital is given by √6h.
(c) The radius of the second orbit of Be+3 is the same as that of the first Bohr orbit of hydrogen atom.
(d) ψ2 = 0 represents an angular wave function.
Answer: (d)
Hint: ψ2 = 0 represents a node.