Tag: TN Board 12th Physics Important Questions Chapter 1

TN State Board 12th Physics Important Questions Chapter 1 Electrostatics

Question 1.
What is meant by electrostatics?
Answer:
Electrostatics is the branch of physics that deals with stationary charges.

Question 2.
What do you know about tritoelectric charging?
Answer:
Tritoelectric charging is the process of charging the objects by a way of rubbing.

Question 3.
How many electrons make up a charge of 3 coulomb?
Answer:
Number of electrons that make up a charge of 3 coulomb
= 3 × 6.25 × 10¹⁸ = 18.75 × 10¹⁸

Question 4.
Mention the properties of charges.
Answer:
(i) Nature of charges
(ii) Conservation of charges
(iii) Quantisation of charges

Question 5.
What happens when an ebonite rod is rubbed with wool?
Answer:
The ebonite rod acquires a negative charge, when wool acquires an equal positive charge.

Question 6.
Why an ebonite rod gets negatively charged when it is rubbed with fur?
Answer:
It is happened because electrons in fur are less tightly bound than electrons in an ebonite rod.

Question 7.
State the value of
(i) proportionality in Coulomb’s law
(ii) the permittivity of free space.
Answer:
(i) The value of the constant k in coulomb’s law
k = 9 × 10⁹ N m²C^-2

(ii) The permittivity of free space
ε₀ = \(\frac{1}{4 \pi k}\) = 8.85 × 10^-12 C² N^-1 m^-2

Question 8.
What is meant by uniform electric field?
Answer:
Uniform electric field will have the same direction and constant magnitude at all points in space.

Question 9.
What is non-uniform electric field?
Answer:
Non-uniform electric field will have different directions or different magnitudes or both at different points in space.

Question 10.
What are the units of
(i) electric field and
(ii) electric flux.
Answer:
(i) Unit of electric field is N / C
(ii) Unit of electric flux is N m² C^-1

Question 11.
What is a dielectric? State examples.
Answer:
A dielectric is a non – conducting material that has no free electrons.
Eg: Ebonite, glass and mica.

Question 12.
What is a Capacitor?
Answer:

1. A capacitor is a device in which electric energy is stored by using a dielectric.
2. A capacitor consists of two plates one of which is charged and the other is insulated metal plate.

Question 13.
Mention the principles of Van de graff generator.
Answer:
(i) Electrostatic induction
(ii) Action at points.

Question 14.
State the principles of conservation of total charges of a body.
Answer:
“The total electric charge in the universe is constant. The charges can neither be created nor be destroyed”. In any physical process, the net change in a charge will always be zero.

Question 15.
State Coulomb’s law.
Answer:
Coulomb’s law states that the electrostatic force is directly proportional to the product of the magnitude of two point charges and inversely proportional to the square of the distance between the two point charges.

Question 16.
Define one Coulomb.
Answer:
One coulomb is defined as the quantity of charge which when placed at a distance of one metre in air or vacuum from an equal and similar charges, experience a repulsive force of 9 × 10⁹ N.

Question 17.
Obtain the value of electric field due to a system of charges.
Answer:
If there are a number of stationary charges, the net electric field at a point is the sum of individual electric fields due to each charge.

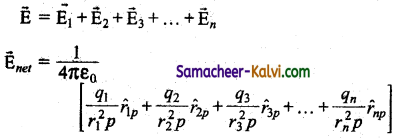
i.e.,
\(\overrightarrow{\mathrm{E}}\)_net = \(\frac{1}{4 \pi \varepsilon_{0}} \sum_{i=1}^{n}\left[\frac{q_{i}}{r_{i}^{2} p} r_{i p}\right]\)

Question 18.
State coulomb’s law in terms of electric field. If the electric field at a point P is E then the force experienced by the test charge placed at that point.
\(\overrightarrow{\mathrm{F}}\) = q₀E

Question 19.
State any three properties of electric field lines.
Answer:
(i) The electric field lines start from a positive charge and end at negative charge or at infinity.
(ii) The number of electric field lines passing through a given surface area perpendicular to the lines is proportional to the magnitude of the electric field in that region.
(iii) They never intersect with each other.

Question 20.
Mention the principle of super position of electric fields.
Answer:
The electric field due to a collection of point charges at an arbitrary point is simply equal to the vector sum of the electric fields created by the individual point charges.

Question 21.
How does water act as a good solvent?
Answer:
When common salt is added to water it acts as a good solvent.

When common salt (NaCl) is added to water, the electrostatic force between Na and Cl irons is reduced to the high relative permitivity of water.

Question 22.
Why is it safer to be inside a bus than standing under a tree on in open ground during lightning?
Answer:
The metal body of the bus provides electrostatic shielding since the electricfield inside the bus is zero.
During lightning, the electric charges flow through the body bus to the ground without affecting the person inside that bus.

Question 23.
State Gauss Law.
Answer:
Gauss Law states that the electric flux of the electric field \(\overrightarrow{\mathrm{F}}\) over any closed surface is equal to \(\frac{1}{\varepsilon_{0}}\) times the net charge enclosed by the surface.

Question 24.
What are non-polar molecules? State examples.
Answer:
In a non-polar molecule, the centres of positive and negative charges coincide.
Eg: H₂, O₂, CO₂ etc.

Question 25.
What are polar molecules? Mention few examples.
Answer:
A polar molecule is one in which the centres of the positive and negative charges are separated even in the absence of an external electric field.
Eg: H₂O, N₂O, HCl, NH₃ etc..

Question 26.
Define Polarisation \(\overrightarrow{\mathrm{p}}\).
Answer:
Polarisation \(\overrightarrow{\mathrm{p}}\) is defined as the total dipole j moment per unit volume of the dielectric.
\(\overrightarrow{\mathrm{p}}\) = χ_e \(\overrightarrow{\mathrm{E}}_{e x t}\)

Question 27.
What is meant by dielectric break down?
Answer:
When a very large external electric field is applied to a dielectric so that the bound electric, charges become free charges. Then electricity is conducted by the dielectrics. This is known as dielectric break down.

Question 28.
Define capacitance of a capacitor.
Answer:
The Capacitance of a capacitor is defined as the ratio of the magnitude of charge on either of the conductor plates to the potential difference existing between the conductors.

C = \(\frac{\mathrm{Q}}{\mathrm{V}}\)

Question 29.
Sometimes/the bladps of the ceiling fan do not start rotating when it is switched on. Give reason from Physics.
Answer:
For the ceiling fan, the initial torque is given by the capacitor (condenser). If the capacitor is faulty than the initial torque required to the rotate the blades when the ceiling fan is switched on is not provided to the blades of the fan.

Question 30.
What are the applications of a capacitor?
Answer:
A capacitor is used
(i) In the digital camera to emit flash of light.
(ii) In heart defibrillator to give a sudden surge of a large amount of electric energy to the patient’s chest. In this way the normal heart function is retrieved.
(iii) In the ignition system of automobile engine to eliminate sparking.
(iv) In power supplies to reduce power fluctuations so that the efficiency of power transmission can be increased.

Question 31.
Where is the principle of corona discharge used?
Answer:
Corona discharge is used in
(i) Lightning arrester.
(ii) Van de graff generator and other electrostatic machines.

Question 32.
State and explain the properties of electric field lines with the help of diagrams.
Answer:
The properties of electric field lines are:
The electric field lines start from a positive charge and end at negative charges or at infinity. For a positive point charge the electric field lines point radially outward and for a negative point charge, the electric field lines point radially inward. (Fig. (a) and (b)).

(a)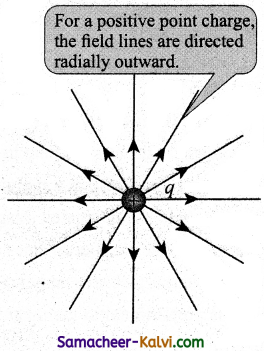

(b)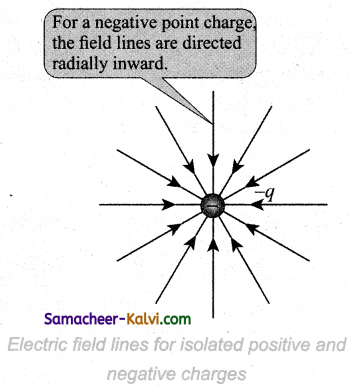

Note that for an isolated positive point charge the electric field line starts from the charge and ends only at infinity. For an isolated negative point charge the electric field lines start at infinity and end at the negative charge.
The electric field vector at a point in space is tangential to the electric field line at that point.

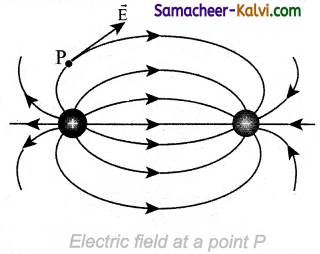
The electric field lines are denser (more close) in a region where the electric field has larger magnitude and less dense in a region where the electric field is of smaller magnitude. In other words, the number of lines passing through a given surface area perpendicular to the lines is proportional to the magnitude of the electric field in that region.

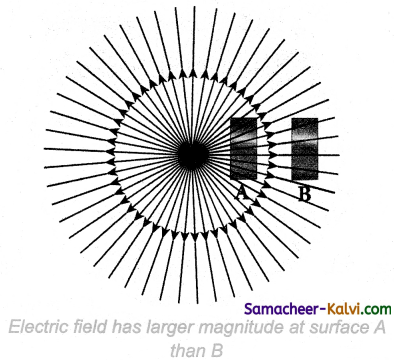
Figure shows electric field lines from a positive point charge. The magnitude of the electric field for a point charge decreases as the distance increases (\(|\overrightarrow{\mathrm{E}}| \propto \frac{1}{r^{2}}\)). So the
electric field has greater magnitude at the surface A than at B.

Therefore the number of lines crossing the surface A is greater than the number of lines crossing the surface B. Note that at surface B the electric field lines are farther apart compared to the electric field lines at the surface A.

No two electric field lines intersect each other. If two lines cross at a point, then there will be two different electric field vectors at the same point.

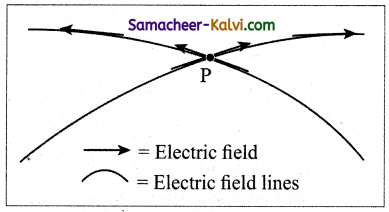
As a consequence, if some charge is placed in the intersection point, then it has to move in two different directions at the same time, which is physically impossible. Hence, electric field lines do not intersect.

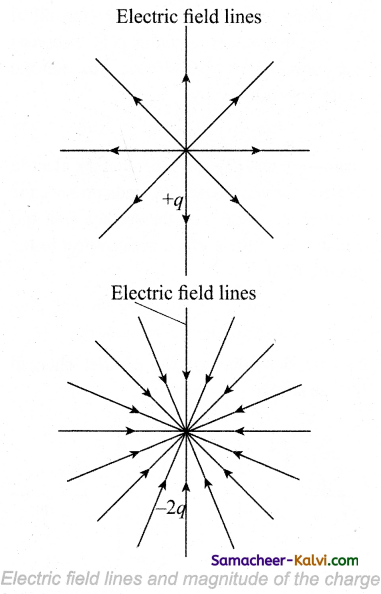
The number of electric field lines that emanate from the positive charge or end at a negative charge is directly proportional to the magnitude of the charges.

For example in the Figure, the electric field lines are drawn for charges +q and -2q. Note that the number of field lines emanating from the +q is 8 and the number of field lines ending at -2q is 16. Since the magnitude of the second charge is twice that of the first charge, the number of field lines drawn for – 2q is twice in number than that for charge +q.

Question 33.
Explain the nature of electric flux for uniform electric field.
Answer:
Electric flux for orm Electric field:
Let us consider a uniform electric field in a region of space. Let us select an area A normal to the electric field lines. (Fig. (a)). The electric flux for this case is

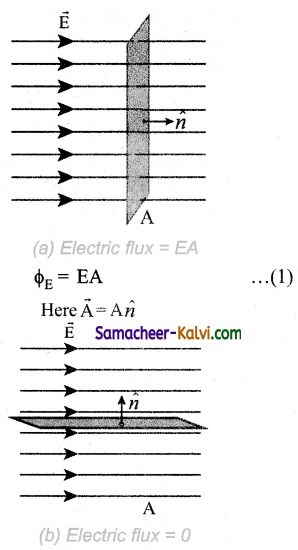
If the same area A is kept parallel to the uniform electric field, then no electric field lines pierce through the area A. (Fig. (b)). The electric flux for this case is zero.

Φ_E = 0 ………….(2)

If the area is inclined at an angle θ with the field, then the component of the electric field perpendicular to the area alone contributes to the electric flux. The electric field component parallel to the surface area will not contribute to the electric flux. (Fig. (c)). For this case, the electric flux

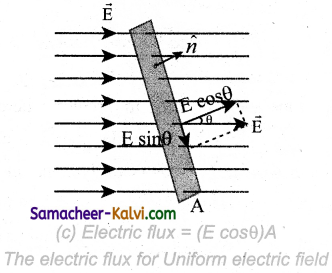
Further, θ is also the angle between the electric field and the direction normal to the area. Hence in general, for uniform electric field, the electric flux is defined as
Φ_E = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\) = EA cos θ ………… (4)

Here, note that \(\overrightarrow{\mathrm{A}}\) is the area vector \(\overrightarrow{\mathrm{A}}\) = A n̂. Its magnitude is simply the area A and the direction is along the unit vector n̂ perpendicular to the area. Using this definition for flux, Φ_E = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\), equations (2) and (3) can be obtained as special cases.

In Figure (a), θ = 0° so Φ_E = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\) = EA
In Figure (b), θ = 90° so Φ_E = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\) = 0

Question 34.
Discuss nature of electric flux in a non uniform electric field and arbitrarily shaped area.
Answer:
If the electric field is not uniform and the area A is not flat (Figure), then the entire area is divided into n small area segments
\(\Delta \overrightarrow{\mathrm{A}}_{1}, \Delta \overrightarrow{\mathrm{A}}_{2}, \Delta \overrightarrow{\mathrm{A}}_{3} \ldots \ldots . \Delta \overrightarrow{\mathrm{A}}_{n}\) such that each area
element is almost flat and the electric field through each area element is considered to be uniform.
The electric flux for the entire area A is approximately written as

\(\begin{aligned}
\phi_{\mathrm{E}} &=\overrightarrow{\mathrm{E}}_{1} \cdot \Delta \overrightarrow{\mathrm{A}}_{1}+\overrightarrow{\mathrm{E}}_{2} \cdot \Delta \overrightarrow{\mathrm{A}}_{2}+\overrightarrow{\mathrm{E}}_{3} \cdot \Delta \overrightarrow{\mathrm{A}}_{3} \ldots \ldots . \overrightarrow{\mathrm{E}}_{n} \cdot \Delta \overrightarrow{\mathrm{A}}_{n} \\
&=\sum_{i=1}^{n} \overrightarrow{\mathrm{E}} \cdot \Delta \overrightarrow{\mathrm{A}}_{1}
\end{aligned}\) ………… (1)

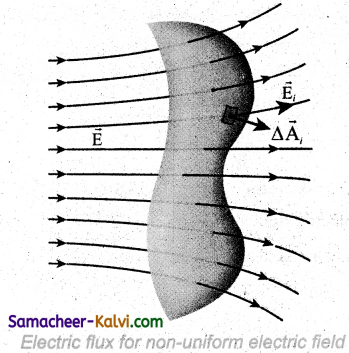
By taking the limit ∆A_i → 0 (for all i) the summation in equation (1) becomes integration. The total electric flux for the entire area is given by
Φ_E = \(\int \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{A}}\) ……..(2)

From Equation (2), it is clear that the electric flux for a given surface depends on both the electric field pattern on the surface area and orientation of the surface with respect to the electric field.

Question 35.
Derive an expression for electric field due to two parallel charged infinite sheets.
Answer:
Electric field due to two parallel charged infinite sheets:

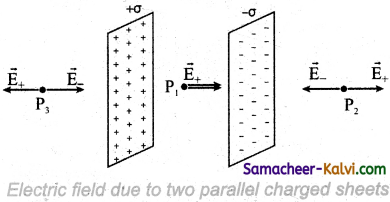
Let us consider two infinitely large charged plane sheets with equal and opposite charge densities +σ and -σ which are placed parallel to each other as shown in the Figure.

The electric field between the plates and outside the plates is found using Gauss law. The magnitude of the electric field due to an infinite charged plane sheet is \(\frac{\sigma}{2 \varepsilon_{0}}\) and it points perpendicularly outward if σ > 0 and points inward if σ < 0.

At the points P₂ and P₃, the electric field due to both plates are equal in magnitude and opposite in direction (Figure). Hence the electric field at a point outside the plates is zero. But inside the plate, electric fields are in same direction i.e., towards the right, the total electric field at a point P₁

E_inside = \(\frac{\sigma}{2 \varepsilon_{\theta}}+\frac{\sigma}{2 \varepsilon_{0}}=\frac{\sigma}{\varepsilon_{0}}\)

The direction of the electric field inside the plates is directed from positively charged plate to negatively charged plate and is f uniform everywhere inside the plate.

Question 36.
Explain the application of capacitor.
Answer:
(i) The applications of capacitor are capacitors is used in most people are now familiar with the digital camera to emit a flash. The flash which comes from the camera when we take photographs is due to the energy released from the capacitor, called a flash capacitor.
(ii) Capacitor is used in the 20 heart defibrillator that is used to give a sudden surge of a large amount of electrical energy to the patient’s chest to retrieve the normal heart function. This defibrillator uses a capacitor of 175 µF charged to a high voltage of around 2000 V.
(iii) Capacitors are used in the ignition system of automobile engines to eliminate sparking.
(iv) Capacitors are used to reduce power fluctuations in power supplies and to increase the efficiency of power transmission.

Question 37.
An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 × 10⁴ Vm^-1. If the density of the oil is 1.26 g cm^-3 then calculate the radius of the drop.
Answer:
Number of electrons = 12
Electric field = 2.55 × 10⁴ Vm^-1
Density ρ = 1.26 × 10³ kg m^-3
As the drop is stationary,
Weight of droplet = force due to electric field
\(\frac{4}{3}\) πr³ ρ g = Eq = E r e

r³ = \(\frac{3 \text { Ere }}{4 \pi \rho g}\)

= \(\frac{3 \times 2.55 \times 10^{4} \times 12 \times 1.6 \times 10^{-19}}{4 \times 3.14 \times 1.26 \times 10^{3} \times 9.8}\)

r³ = 0.94 × 10^-18
∴ r = (0.94 × 10^-18)^1/3.
= 9.81 × 10^-7 m
∴ Radius of the drop = 9.81 × 10^-7 m

Question 38.
An electric dipole of charges 2 × 10^-6 C, – 2 × 10^-6 C are separated by a distance 1 cm. Calculate the electric field due to dipole at a point on its.
(i) axial line 1 m from its centre
(ii) equatorial line 1 m from its centre.
Answer:
Charges are q₁ = 2 × 10^-6 C;
q₂ = – 2 × 10^-6 C;
Distance of separation r = 1 cm = 10^-2 m.
Electric field due to dipole at a point on the axial line is

E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 p}{r^{3}}\); P = q × 2d

Electric field due to dipole at a point on the equatorial line is

E = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{P}{r^{3}}\)

Electric field due to dipole at a point on the axial line

E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \mathrm{P}}{r^{3}}\)

P = q × 2 d = 2 × 10^-6 × 10^-2 = 2 × 10^-8

E = \(\frac{9 \times 10^{9} \times 2 \times 2 \times 10^{-8}}{1^{3}}\)
= 36 × 10¹
= 360 NC^-1

Electric field due to dipole at a point 1m from its center on the equatorial line is

E = \(\frac{\mathrm{P}}{4 \pi \varepsilon_{0} r^{3}}\)

P = q × 2d = 2 × 10^-6 × 1 × 10²
= 2 × 10^-8 cm

E = \(\frac{9 \times 10^{9} \times 2 \times 10^{-8}}{1^{3}}\)

= 18 × 10^-1 = 180 N⁺C^-1

Electric field along axial line = 360 N⁺C^-1.
Electric field along equatorial line = 180 NC^-1.

Question 39.
A spherical conductor of radius 0.12 m has a charge of 1.6 × 10^-7 C distributed uniformly on its surface. What is the electric field
(i) inside the sphere
(ii) on the sphere
(iii) at a point 0.18 m from the centre of the sphere?
Answer:
Radius of a sphere r = 0.12 m;
Charge of a sphere q = 1.6 × 10^-7 C.
(i) Electric field inside the sphere = 0
(ii) Electric field on the sphere

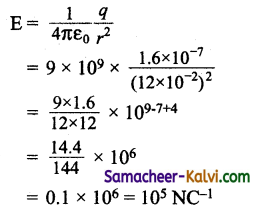
(iii) Electric field at a point 0.18 m from the centre of the sphere

Electric field inside the sphere = 0
Electric field on the sphere = 10⁵ NC^-1
Electric field at a point 0.18 m from the centre of the sphere = 4.44 × 10⁴ NC^-1

Question 40.
An electric charge 1.6 × 10^-19 C is situated in a uniform field of intensity 120000Vm^-1. Find the force on it, its acceleration and the time it takes to travel 20mm from rest. (Electron mass m = 9.1 × 10^-31 kg)
Answer:
Given:
E = 120000 Vm^-1;
e = 1.6 × 10^-19 C

Working: .
∴ F = Ee;
F = 1.6 × 10^-19 × 1.2 × 10⁵
= 1.92 × 10^-14 N
Acceleration a = \(\frac{\mathrm{F}}{m}=\frac{1.92 \times 10^{-4}}{9.1 \times 10^{-31}}\)
= 2.12 × 10¹⁶ ms^-2

Time taken to travel 20 mm or 0.02 m is given by
s = \(\frac{1}{2}\) at²

t = \(\sqrt{\frac{2 s}{a}}=\sqrt{\frac{2 \times 0.02}{2.12 \times 10^{16}}}\)

= 1.37 × 10^-9 s

Force F = 1.92 × 10^-14 N
Acceleration a = 2.12 × 10×16 ms^-2
Time taken to travel 20 mm from rest t = 1.37 × 10^-9 s

Question 41.
Calculate the electric potential energy of electron-protonsystemofhydrogenatom.The radius ofthe electron orbit r = 5.92 × 10^-10 m; Electron charge e = 1.6 × 10^-19 C.
Answer:
r = 5.92 × 10^-10 m;
e = 1.6 × 10^-19 C
The electric potential energy of electron- proton system

Question 42.
Two fixed point, charges + 4q and + q are separated by a distance d. Where should the third point charge be placed for it to be in equilibrium?
Answer:
The charges are q₁ = +4q and q₂ = +q.
Distance between the charges = d
Force between the charges

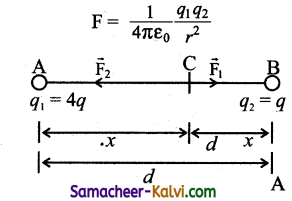
AB = d, AC = q; CB = d – x
Let a charge q be placed between two charges.
Force on the charge C exerted by A is given by

F₁ = \(\frac{q(4 q)}{4 \pi \varepsilon_{0} x^{2}}\) directed away from A (4q)

Force on the charge C exerted by B is given by

F₂ = \(\frac{q(q)}{4 \pi \varepsilon_{0}(d-x)^{2}}\) directed away from B (q).

For the charge q to be in equilibrium,
F₁ = F₂

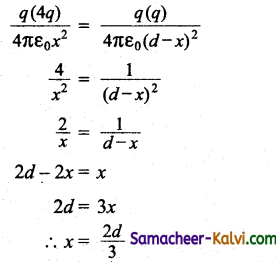
The charge q should be placed at a distance from charge 4q.

Question 43.
A charged particle of mass 1.0 g is suspended through a silk thread of length 40 cm in a horizontal electric field of 4 × 10 ⁴ N/C. If the particle stays at a distance of 24 cm from the wall in equilibrium, calculate the charge on the particle.

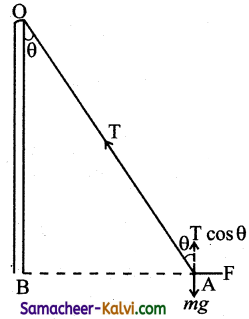
Answer:
Mass of the particle m = 10^-3 kg
Length of a silk thread OA = 40 cm = 0.4 m;
Electric field E = 4 × 10⁴ N/C
Distance AB = 0.24 m
In equilibrium,
F = T sin θ ………..(1)
mg = T cos θ …………(2)
Dividing equation (1) by (2) we get

Charge q = 1.8 × 10^-7 C.

Question 44.
Calculate the electric potential energy of the system of charges shown in the figure.

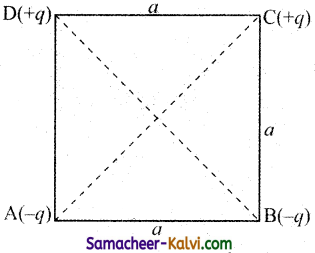
Answer:
Let the charges -q, -q, +q and +q are located at the comers of a square A, B, C and D.

Potential energy P.E. = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r}\)

Taking zero of potential energy at infinity we get P.E. of the system of charges.

Potential energy = \(\frac{-18 q^{2}}{a \sqrt{2}}\) × 109 J.

Question 45.
A square of side 1.3 m has charges +12 nC, -24nC, +31 nC and +17 nC at its corners. Calculate the electric potential at the centre of the square.
Answer:
q₁ = +12 nC;
q₂ = -24 nC;
q₃ = +31 nC;
q₄ = +17 nC;
d = 1.3 m

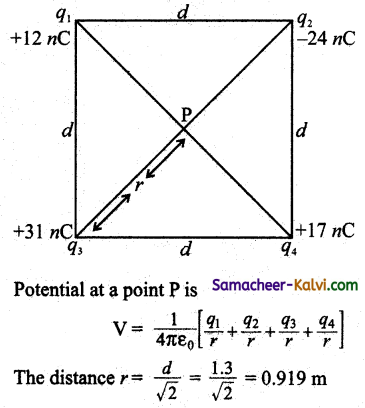
Total charge = q₁ + q₂ + q₃ + q₄
= (12 – 24 + 31 + 17) × 10^-9
q = 36 × 10^-9
∴ V = \(\frac{9 \times 10^{9} \times 36 \times 10^{9}}{0.919}\)

V = 352.6 V

Question 46.
Two charges of -4 µC and +4 µC are placed at the points A(1, 0, 4) and B (2, -1, 5) located in an electric field E = \(\overrightarrow{\mathrm{E}}=0.20 \hat{i}\) V / cm. Calculate the torque acting on the dipole.
Answer:
As A(1, 0, 4), B (2, -1, 5)
∴ 2a = A\(\overrightarrow{\mathrm{B}}\)
= [(2 – 1)î + (- 1 – 0)ĵ + (5 – 4)k̂]
= [î – ĵ + k̂]
Charge q = ± 4 × 10^-6 C
Electric field E = 0.20 î V / cm = 20 î V / m
Torque acting on the dipole
τ = \(\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{E}}\)
τ = q(2\(\vec{a}\)) × E
= 4 × 10^-6 (î + ĵ + k̂) × 20 î
= 8 × 10^-5 (k̂ + ĵ)

Magnitude of torque
τ = 8 × 10^-5 \(\sqrt{1^{2}+1^{2}}\)
= 8 × 10^-5 × √2
= 8 × 10^-5 × 1.414
= 11.312 × 10^-5 N m

Question 47.
An infinite number of charges each numerically equal to q and of the same sign are placed along x – axis at x = 1, x = 2, x = 4, x = 8 and so on.
Calculate the electric potential at x = 0.
Answer:
From, super position principle, we get electric potential at the origin (x – 0) due to various charges as, q

Question 48.
If one of the two electrons of a hydrogen molecule is removed, we get a molecular ion (H₂⁺). In the ground state of H₂⁺, the two protons are separated by 1.5 Å and electron is 1 Å from each proton. Determine the potential energy of the system.
Answer:
q₁ = Charge on electron = 1.6 × 10^-19 C
q₂, q₃ – Charge on two protons = 1.6 × 10^-19 C
Distance between q₁ and q₂ is
r₁₂ = 1 Å = 1 × 10^-10 m
Distance between q₂ and q₃ is
r₂₃ = 1.5 Å = 1.5 × 10^-10 m
Distance between q₃ and q₁ is
r₃₁ = 1 Å = 10^-10 m
Potential energy

Question 49.
The electric field in a region is given by \(\overrightarrow{\mathrm{E}}=\frac{3}{5} \mathrm{E}_{0} \hat{i}+\frac{4}{5} \mathrm{E}_{\alpha} \hat{j}\) with E₀ = 2 × 10³ N / C.
Calculate the electric flux of this field through a rectangular^surface of area 0.2 m2 parallel to the Y – Z plane.
Answer:
\(\overrightarrow{\mathrm{E}}=\frac{3}{5} \mathrm{E}_{0} \hat{i}+\frac{4}{5} \mathrm{E}_{\alpha} \hat{j}\)
Where E₀ = 2 × 10³ N / C.
Area = 0.2 m² parallel to YZ plane.
Normal to the area will be along x – axis
electric flux is Φ = E_x × A
= \(\frac{3}{5}\) E₀ × 0.2
= \(\frac{0.6}{5}\) × 2 × 10³
Electric flux Φ = 240 N m² C^-1

Question 50.
Find the electric flux through each face of a hollow cube of side 10 cm, if a charge of 8.85 μC is placed at the centre.
Answer:
The side of a hollow cube = 10 × 10^-2 m;
Charge q = 8.85 × 10^-6 C

Total number of sides of a hollow cube = 6
According to Gauss’s theorem the electric flux through each force is given by,

Φ = \(\frac{1}{6} \frac{q}{\varepsilon_{0}}=\frac{1}{6} \times \frac{8.85 \times 10^{-6}}{8.85 \times 10^{-12}}\)

= \(\frac{1 \times 10^{6}}{6}\) = 1.6 × 10⁵ Nm² C^-1
Electric flux through each face = 1.6 × 10⁵ Nm² C^-1

Question 51.
Two positive charges of 12 μC and 8 μC respectively are 10 cm apart. Find the work done in bringing them 4 cm closer, so that, they are 6 cm apart.
Answer:
The charges are q₁ = 12C; q₂ = 8C
Distance between the charges r_B = 10 × 10^-2 m
Distance between the charges r_A = 6 × 10^-2 m

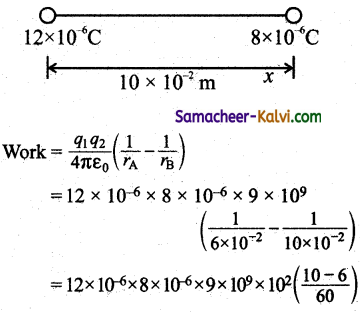
= 12 × 10^-6 × 8 × 10^-6 × 9 × 10¹¹ × \(\frac{4}{60}\)

= \(\frac{96 \times 36}{60}\) × 10¹¹ × 10^-12
= 57.6 × 10¹¹ × 10^-12
= 57.6 × 10^-1 = 57.6
work = 57.6

Question 52.
Find the work done in bringing a charge of +10 × 10^-4 µC from infinity to apart 25 cm from the charge of +3 × 10^-2 µC.
Answer:
q₁ = 10 × 10^-4 µC;
q₂ = 3 × 10^-2 µC;
r = 25 × 10^-2 m
Work done represents the electric potential energy (U) of the system of charge q₁ and q₂.
U = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)

U = \(\frac{9 \times 10^{9} \times 10 \times 10^{-4} \times 10^{-6} \times 3 \times 10^{-2} \times 10^{-6}}{25 \times 10^{-2}}\)
= 10.8 × 10^-7 joules

Question 53.
The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge – 0.8 µC in air is 0.2 N. Calculate the distance between two spherical charges. What is the force on the second sphere due to the first?
Answer:
The charges are q₁ = 0.4 × 10^-6 C;
q₂ = – 0.8 × 10^-6 C.
Force between the two charges F = 0.2 N
Force between the charges F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
Distance between two spherical charges is given by
r² = \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} \mathrm{~F}}\)

= \(\frac{9 \times 10^{9} \times 0.4 \times 10^{-6} \times 0.8 \times 10^{-6}}{0.2}\)
= 16 × 9 × 10^-4
∴ r = 4 × 3 × 10^-2 m = 0.12 m
Distance between two charges = 0.12 m
Force on second sphere is same F₂ = 0.2 N.

Question 54.
The electric field outside a charged long straight wire is given by E = \(\frac{1000}{r}\) V m^-1, and is directed outwards.
(a) What is the sign of the charge on the wire.
(b) If two points A and B are situated in such a way that r_A = 0.2 m and r_B = 0.4 m then Calculate the value of (V_B – V_A).
Answer:
(a) The charge on the wire must be positive

Question 55.
A parallel plate capacitor consists of two identical circular plates of radius 3cm which are separated by 2.5mm. Calculate the capacitance. What will be its capacitance if the separation is reduced to half the initial value?
Answer:
Radius of each plate
r = 3 cm = 3 × 10^-2 m
∴ Area of each plate A = πr²
= π (3 × 10^-2)² = 28.27 × 10^-4 m²
Distance between plates d = 2.5 mm = 2.5 × 10^-3 m
Absolute permittivity of air
ε₀ = 8.854 × 10^-12 C² N^-1 m^-2
Capacitance of the capacitor
C = \(\frac{\varepsilon_{0} \mathrm{~A}}{d}\)

= \(\frac{8.854 \times 10^{-12} \times 28.27 \times 10^{-4}}{2.5 \times 10^{-3}}\)

= 100 × 10^-13 F
= 10 × 10^-12 F
= 10 pF

Question 56.
A parallel plate air capacitor has the same capacity as that of a spherical conductor of diameter 1.2 m. If the plates of the parallel plate capacitor are separated by a distance of 0.2 m, calculate the area of the plates.
Answer:
Diameter D = 1.2 m
Radius r = 0.6 m
Distance between plates d = 0.2 m
Capacity of parallel plate capacitor = Capacity of spherical conductor
\(\frac{\varepsilon_{0} \mathrm{~A}}{d}\) = 4πε₀r
where A = area of the plates
A = 4πrd = 4π × 0.6 × 0.2
Area of the plates = 1.51 m²

Question 57.
A parallel plate condenser is made up of 26 metal strips each 3 cm by 4 cm separated by sheets of mica of dielectric constant 6 and uniform thickness of 0.2mm. Calculate it capacity.
Answer:
A= 0.03 × 0.04 = 12 × 10^-4 m²
n = (26 – 1) = 25
ε^r = 6
ε⁰ = 8.854 × 10^-12 C² N^-1 m^-2
d = 0.2 mm = 2 × 10^-4 m

C = \(\frac{n \varepsilon_{0} \varepsilon_{r} \mathrm{~A}}{d}\)

= \(\frac{25 \times 8.854 \times 10^{-12} \times 6 \times 12 \times 10^{-4}}{2 \times 10^{-4}}\)
= 7.965 × 10^-9 F
Capacity = 7.965 × 10^-9 F

Question 58.
Two capacitors of capacity 200 pF and 600 pF are connected in parallel and then charged to a potential of 120 V. Determine
(a) the charge on each capacitor;
(b) the total charge and
(c) the effective capacity of the combination.
Answer:
Here C₁ = 200 × 10^-12 F;
C₂ = 600 × 10^-12 F;
V = 120 V
(a) Charge on first capacitor,
q₁ = C₁ V
= 200 × 10^-12 × 120 = 24 × 10^-9 C
Charge on second capacitor,
q₂ = C₂V
= 600 × 10^-12 × 120 = 72 × 10^-9 C

(b) Total charge
q = q₁ + q₂
= (24 × 10^-9) + (72 × 10^-9)
= 96 × 10^-9 C

(c) Let the effective capacity be C.
Capacitors are connected in parallel.
C = C₁ + C₁
= 200 × 10^-12 + 600 × 10^-12
= 800 × 10^-12 F
C = 800 μ F = 800 pF

(a) q₁ = 24 × 10^-9 C;
q₂ = 72 × 10^-9 C
(b) Total charge q = 96 × 10^-9 C
(c) Effective capacitance C = 800 pF

Question 59.
A 4 μF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2 μF capacitor. How much electrostatic energy of the capacitor is dissipated in the form of heat?
Answer:
Capacitance of first Capacitor
C₁ = 4 × 10^-6 F
V₁ = 200 V
Initial electrostatic energy is C₁ is
E₁ = \(\frac{1}{2}\) C₁V₁²
= \(\frac{1}{2}\) × 4 × 10^-6 (200)²
E₁ = 8 × 10^-2 J ……….(1)
Capacitance of another capacitor
C₂ = 4 p F
When C₂ is connected to C₁, charge flows and both acquire a common potential

From equation (1) and (2) we get energy dissiputedintheformofheat
= E₁ – E₂ = 8 × 10^-2 – 5.33 × 10^-2
= 2.67 × 10^-2 J

Question 60.
Three capacitors of 1 µF, 2 µF and 3 µF are joined in series first and then in parallel. Calculate the ratio of equivalent capacitance in two cases.
Answer:
C₁ = 1 µF, C₂ = 2 µF, C₃ = 3 µF Series:
Series:

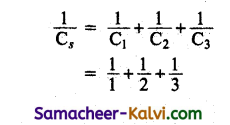
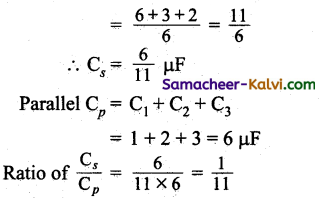
Question 61.
A dielectric of relative permittivity 3 fills up only three fourth of the space between the plates of a charged parallel plate capacitor. Calculate the percentage of energy stored in the dielectric.
Answer:
C₁ = \(\frac{\varepsilon_{0} \mathrm{~A}}{d}\)

Energy stored in a capacitor E₁ = \(\frac{\mathrm{Q}^{2}}{2 \mathrm{C}_{1}}\)

An introducing the dielectric of thickness t = \(\frac{3}{4}\) d and k = 3
The new capacitance,

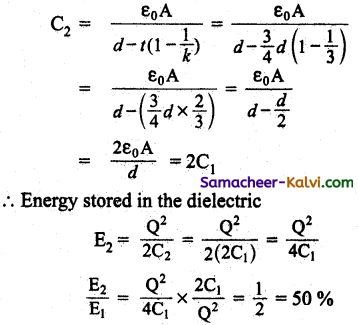
Choose the correct answer:

Question 1.
Which one of the following statements gives correct reason for ‘The charge given to any conductor resides on its outer surface only:
(a) the free charge tends to be in its state of maximum potential energy.
(b) the free charge tends to be in its state of minimum potential energy.
(c) the free charge tends to be in its state of minimum kinetic energy.
(d) the free charge tends to be in its state of maximum kinetic energy.
Answer:
(c) the free charge tends to be in its state of minimum kinetic energy.

Question 2.
Assertion:
For practical purpose, the earth is used as a reference at zero potential in electrical circuits.
Reason:
The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by \(\frac{Q}{4 \pi \varepsilon_{0} R}\)
Which one of the following statements is correct?
(a) Both Assertion and Reason are true and reason explains assertion correctly.
(b) Both Assertion and Reason are true and reason does not explain assertion correctly.
(c) Assertion is true but reason is false.
(d) Assertion is false but reason is true.
Answer:
(b) Both Assertion and Reason are true and reason does not explain assertion correctly.

Question 3.
Consider the points lying on a straight line joining two fixed opposite charges. Between the charges there is:
Which of the following statements are correct?

(i) No point where electric field is zero.
(ii) Two points where electric potential is zero.
(iii) No point where electric potential is zero.
(iv) Three points where electric field is zero.

(a) statements (i) and (iii) are correct
(b) statements (i) and (ii) are correct
(c) statements (iii) and (iv) are correct
(d) statements (i) and (iv) are correct
Answer:
(b) statements (i) and (ii) are correct

Question 4.
When an electron is sent in electric field of 9.1 × 10⁶ N/C, the acceleration produced is ………….. m/s².
(a) 0.8 × 10¹⁸
(b) 1.6 × 10^-18
(c) 3.2 × 10¹⁸
(d) 1.6 × 10¹⁸
Answer:
(d) 1.6 × 10¹⁸
Hint:
F_e = eE
∴ ma = eE
a = \(\frac{e \mathrm{E}}{m}\)

= \(\frac{1.6 \times 10^{-19} \times 9.1 \times 10^{6}}{9.1 \times 10^{-31}}\)
= 1.6 × 10¹⁸

Question 5.
Choose the odd man out of the following:
(a) dipole moment
(b) electric potential
(c) electric field
(d) electric flux
Answer:
(c) electric field
Hint:
Electric field is a vector and others are scalars.

Question 6.
A conducting sphere of radius 20 cm gives a charge of 16pC. The electric field at its centre will be:
(a) 1.8 × 10⁴ N / C
(b) 3.6 × 10⁴ N / C
(c) Zero
(d) 0.9 × 10⁴ N/C
Answer:
(c) Zero
Hint:
Electric field inside a conductor is zero.

Question 7.
Consider a neutral conducting sphere. A positive point charge is placed outside the sphere. The net charge on the sphere is then:
(a) negative only a point on the sphere.
(b) zero
(c) negative and distributed uniformly over the surface of the sphere.
(d) negative and distributed non – uniformly over the surface of the sphere.
Answer:
(b) Zero
Hint:
When a positive point charge is placed outside, the neutral conducting sphere having no charge. Hence the net charge on the sphere is zero.

Question 8.
If a system consists of three charges 3q, 4q and -5q, then total charge of the system is:
(a) – 2q
(b) 2q
(c) 5q
(d) -3q
Answer:
(b) 2q

Question 9.
If a proton is moved against the Coulomb force of an electric field:
(a) work is done by the electric field
(b) energy is used from some outside source
(c) the strength of the field is decreased
(d) the energy of the system is decreased
Answer:
(b) energy is used from some outside source

Question 10.
The unit of permittivity is:
(a) C² N^-1 m^-2
(b) N m² C^-2
(c) N m^-1
(d) N C^-2 m^-2
Answer:
(a) C² N^-1 m^-2

Question 11.
The number of electric lines of force originating from a charge of 1 C is:
(a) 1.129 × 10¹¹
(b) 1.6 × 10^-19
(c) 6.25 × 10¹⁸
(d) 8.85 × 10¹²
Answer:
(a) 1.129 × 10¹¹

Question 12.
Which of the following quantities is scalar?
(a) Dipole moment
(b) Electric force
(c) Electric field
(d) Electric potential
Answer:
(d) Electric potential

Question 13.
The permittivity of vacuum ε₀ equals:

(a) 9 × 10⁹ Nm²C^-2

(b) \(\frac{1}{9 \times 10^{9}} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

(c) \(\frac{1}{9 \times 10^{9} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

(d) \(\frac{1}{4 \pi \times 9 \times 10^{9}} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

Answer:
(d) \(\frac{1}{4 \pi \times 9 \times 10^{9}} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

Question 14.
A bullet of mass 2g has a charge of 2 µC. The potential difference through which it must be accelerated from rest to acquire a speed of 10 ms^-1 is:
(a) 5 V
(b) 50 V
(c) 5 kV
(d) 50 kV
Answer:
(d) 50 kV
Hint:
Work done = kinetic energy

Question 15.
If an ebonite rod is rubbed with fur, it:
(a) becomes positively charged
(b) becomes negatively charged
(c) loses negative charge
(d) becomes uncharged
Answer:
(b) becomes negatively charged

Question 16.
An example of conductor is:
(a) nonmetal
(b) human body
(c) dry wood
(d) None of the above
Answer:
(b) human body

Question 17.
Coulomb’s inverse square law deals with:
(a) The force between two point charges
(b) The force of attraction between two or three charges
(c) The force of attraction between two charges
(d) None of the above
Answer:
(a) The force between two point charges

Question 18.
When two point charges + 6 C and – 5 C experiences a force of 2.7 × 10¹¹ N, the distance between them is:
(a) 0.5 m
(b) 1 m
(c) 10 m
(d) 10 cm
Answer:
(b) 1 m

Question 19.
Force between the charges is given by the equation
(a) F = \(\frac{k q_{1} q_{2}}{r^{2}}\)

(b) F = \(\frac{k q_{1} q_{2}}{r^{3}}\)

(c) F = \(\frac{k q_{1} q_{2}}{q 2^{r}}\)

(d) F = \(\frac{\mathrm{K} q_{1} q_{2}}{q_{1} r}\)
Answer:
(a) F = \(\frac{k q_{1} q_{2}}{r^{2}}\)

Question 20.
If the distance between two charges is doubled the electrostatic force between the charges will be:
(a) four times more
(b) four times less
(c) two times more
(d) two times less
Answer:
(b) four times less

Question 21.
A given charge is situated at a certain distance from an electric dipole in the end-on position experiences a force F.
If the distance of the charge is doubled, then the force acting on the charge will be:

(a) \(\frac{F}{2}\)

(b) 2F

(c) \(\frac{F}{8}\)

(d) \(\frac{F}{4}\)
Answer:
(c) \(\frac{F}{2}\)
Hint:
F = qE = q × k × \(\frac{2 p}{r^{3}}\)

∴ F ∝ \(\frac{1}{r^{3}}\)

when r is doubled,

F₁ ∝ \(\frac{1}{(2 r)^{3}}\)
= \(\frac{1}{8}\) times F

F₁ = \(\frac{F}{8}\)

Question 22.
An isolated point charge is given a charge q. The potential at a distance r is:

(a) \(\frac{q^{2}}{4 \pi \varepsilon_{\theta} r}\)

(b) \(\frac{q}{4 \pi \varepsilon_{0} r}\)

(c) \(\frac{q}{8 \pi \varepsilon_{0} r}\)

(d) \(\frac{q^{2}}{8 \pi \varepsilon_{0} r}\)
Answer:
(b) \(\frac{q}{4 \pi \varepsilon_{0} r}\)

Question 23.
An electric dipole with dipole moment 4 × 10^-9 cm is kept at 30° with the direction of uniform electric field of magnitude 5 × 10⁴ NC^-1. The magnitude of torque on the dipole is:
(a) 10^-4 Nm
(b) 10^-5 Nm
(c) 10⁴Nm
(d) 2 × 10^-5 Nm
Answer:
(a) 10^-4 Nm

Question 24.
(a)The electric field E and potential V at a point are related to one another as:

(a) E = – \(\frac{d r}{d V}\)

(b) E = \(\frac{d V}{d r}\)

(c) E = – \(\frac{d V}{d r}\)

(d) E = + \(\frac{d r}{d V}\)

Answer:
(c) E = – \(\frac{d V}{d r}\)

Question 25.
When a point P lies on the axial line of the dipole on the side of the positive charge then the potential is:

(a) V = \(\frac{P}{4 \pi \varepsilon_{0} r^{2}}\)

(b) V = – \(\frac{P}{4 \pi \varepsilon_{0} r^{2}}\)

(c) V = 0

(d) V = \(\frac{P}{4 \pi \varepsilon_{0} r^{3}}\)
Answer:
(a) V = \(\frac{P}{4 \pi \varepsilon_{0} r^{2}}\)

Question 26.
The strength at any point inside the electric field is defined by:
(a) Force experienced by a unit positive charge
(b) Force of repulsion experienced by a unit negative charge
(c) Force experienced by a positive charge
(d) None of the above
Answer:
(a) Force experienced by a unit positive charge

Question 27.
Lines of forces is represented by the path followed by …………. in an electric field.
(a) positive charge
(b) unit positive charge
(c) unit negative charge
(d) None of the above
Answer:
(b) unit positive charge

Question 28.
The surface charge density will be greater if:
(a) greater the radius of curvature at any point
(b) smaller the radius of curvature at any point
(c) the surface is plain
(d) None of the above
Answer:
(a) greater the radius of curvature at any point

Question 29.
The electric field due to jlipole at a point on the equatorial line given by:
(a) E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \mathrm{P}}{r^{3}}\)

(b) E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{P}{r^{3}}\)

(c) E = \(\frac{P}{\pi \varepsilon_{0} r^{2}}\)

(d) E = \(\frac{1}{4 \pi} \frac{\mathrm{P}}{r^{3}}\)

Answer:

(b) E = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{P}{r^{3}}\)

Question 30.
The electric potential energy U of the system of charges and q2 is:

(a) \(\frac{1}{4 \pi \varepsilon_{0}} \frac{d}{q_{1} q_{2}}\)

(b) \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{d}\)

(c) \(\frac{1}{4 \pi \varepsilon_{0}} \frac{d^{2}}{q_{1} q_{2}}\)

(d) \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{d^{2}}\)

Answer:
(d) \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{d^{2}}\)

Question 31.
An electric dipole placed at an angle 0 in a non-uniform electric field experiences:
(a) neither a force nor a torque
(b) torque only
(c) both force and torque
(d) force only
Answer:
(c) both force and torque

Question 32.
The law that governs the force between electric charges is:
(a) Ampere’s law
(b) Faraday’s law
(c) Coulomb’s law
(d) Ohm’s law
Answer:
(c) Coulomb’s law

Question 33.
Electric dipole consists of:
(a) two similar charges, separated by a small distance
(b) two dis-similar charges separated by a small distance
(c) two similar charges separated by a large distance
(d) many charges
Answer:
(b) two dis-similar charges separated by a small distance

Question 34.
According to Gauss theorem:
(a) Φ q = ε₀

(b) Φ = \(\frac{q}{\varepsilon_{0}}\)

(c) ε₀ = \(\frac{\phi}{q}\)

(d) Φ = \(\frac{\varepsilon_{0}}{q}\)
Answer:
(b) Φ = \(\frac{q}{\varepsilon_{0}}\)

Question 35.
Two point charges A and B of + 5nC and + 3nC are kept at 6 cm apart in air medium. The work required to more charge B towards charge A through 1cm is:
(a) 3.5 × 10^-7 J
(b) 4.5 × 10^-7 J
(c) 4.5 × 10^-11 J
(d) 3.5 × 10^-10 j
Answer:
(b) 4.5 × 10^-7 J
Hint:
work = change in P.E

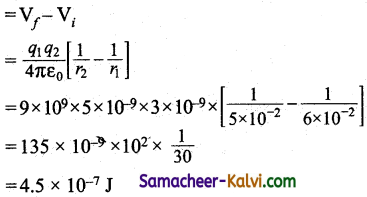
Question 36.
Match the given physical quantities in Column I with the units given in Column II:

Column I	Column II
(i) Electric field	(A) N C-1 m2
(ii) Electric potential	(B) C-2 N-1 m2
(iii) Electric permittivity	(C) volt
(iv) Electric flux	(D) N C-1

(a) (i) – (A); (ii) – (B); (iii) – (D); (iv) – (C)
(b) (i) – (D); (ii) – (C); (iii) – (B); (iv) – (A)
(c) (i) – (D); (ii) – (C); (iii) – (A); (iv) – (B)
(d) (i) – (A); (ii) – (D); (iii) – (B); (iv) – (C)
Answer:
(b) (i) – (D); (ii) – (C); (iii) – (B); (iv) – (A)

Question 37.
Choose the scalar quantity (odd man out) from the following:
(a) Electric field
(b) Electric potential
(c) Electric force
(d) Dipole moment
Answer:
(b) Electric potential

Question 38.
The electric field lines of a positive charge and a negative charge are shown in the following figure.

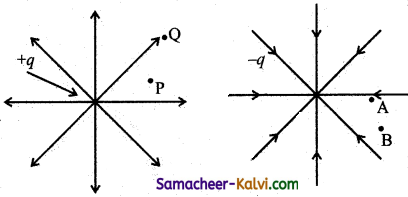
Which of the following statements is incorrect?
(a) Potential energy at A is greater than that at B.
(b) Potential energy at P is less than that at Q.
(c) Potential at A is greater than that at B.
(d) Potential at P is greater than that at Q.
Answer:
(c) Potential at A is greater than that at B.

Question 39.
A sphere of radius R is made up of a conducting material and carries a charge Q. Select the correct statements from the following:
(i) The electric field is zero inside the sphere.
(ii) The electric field is perpendicular to the surface of the sphere.
(iii) No work is done to move a charge from one point to another.
(iv) Charge Q resides on the surface of the sphere.

(a) statements (i) and (ii)
(b) statements (ii) and (iii)
(c) statements (i), (ii), and (iii)
(d) statements (i), (ii), (iii) and (iv)
Answer:
(d) statements (i), (ii), (iii) and (iv)

Question 40.
The magnitude of the electric field at a point P at a distance of 3 m from a point charge Q is 100 V m^-1:
(i) Q = 4.0 µC
(ii) The value Q = 10^-7 C
(iii) The value V = 1.8 × 10⁴V
(iv) The electric potential at P is V = 3 × 10⁴ V
Which of the following statements are correct?
(a) statements (ii) and (iv)
(b) statements (iii) and (iv)
(c) statements (i) and (ii)
(d) statements (i) and (iv)
Answer:
(c) statements (i) and (ii)
Hint:

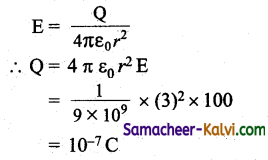
V = \(\frac{\mathrm{Q}}{4 \pi \varepsilon_{0} r}\)

= \(\frac{10^{-7} \times 9 \times 10^{9}}{3}\)

= 3 × 10² V

Question 41.
Which one of the following is correct for the following situation for the given surface S, Gauss law states that the electric field E is due to all the charges placed:
(a) On the surface S
(b) inside the surface S
(c) outside the surface S
(d) inside and outside surface S
Answer:
(d) inside and outside surface S

Question 42.
Assertion:
If electric field is zero at a point then electric potential also be zero at that point.
Reason:
Electric field is equal to the negative gradient of potential.
Which one of the following statements is correct?
(a) Both Assertion and reason are true and reason explains assertion correctly.
(b) Both Assertion and Reason are true and reason does not explain assertion correctly.
(c) Assertion is true and reason is false.
(d) Assertion is false and reason is true.
Answer:
(d) Assertion is false and reason is true.
Hint:
Since E = \(\frac{-d \mathrm{~V}}{d r}\)
If E = 0 then V = constant but not necessarily equal to zero.

Question 43.
Assertion:
When a test charge is released in a uniform electric field* then it will moves along the fixed line passing through that point
Reason:
The tangent at a point on the electric field gives the direction of the electric field at that point.
(a) Both Assertion and reason are true and reason does not explain assertion.
(b) Both Assertion and reason are true and reason explains assertion correctly.
(c) Assertion is false and reason is true.
(d) Assertion is true and reason is false.
Answer:
(c) Assertion is false and reason is true.

Question 44.
Assertion:
A parallel plate capacitor is charged by a battery, when battery is disconnected, if the space between the plates is filled with a dielectric, then energy stored will increase.
Reason:
Due to the introduction of dielectric the capacitance will be increased.
(a) Both Assertion and Reason are false.
(b) Assertion is true and reason is false.
(c) Both assertion and reason are true and reason explain assertion correctly.
(d) Both assertion and reason are true and reason does not explain assertion correctly.
Answer:
(d) Both assertion and reason are true and reason does not explain assertion correctly.
Hint:
Energy U = \(\frac{\mathrm{Q}^{2}}{2 \mathrm{C}}\)
As battery is disconnected the charge Q remains same. Hence C increases and energy will be decreased.

Question 45.
The inner and outer radii of a spherical capacitor are r₁ and r₂ respectively. When the inner surface is earthed. The outer sphere is given a charge +Q, then the charge on the inner surface of the outer sphere is Q” is:

(a) \(\frac{\mathrm{Q}\left(r_{a}-r_{b}\right)}{r_{b}}\)

(b) \(\frac{\mathrm{Q}\left(r_{b}-r_{a}\right)}{r_{a}}\)

(c) \(\frac{\mathrm{Q} r_{b}}{r_{a}}\)

(d) \(\frac{\mathrm{Q} r_{a}}{r_{b}}\)

Answer:
(d) \(\frac{\mathrm{Q} r_{a}}{r_{b}}\)

Hint:
Q” = Q – Q’

= Q – \(\frac{\mathrm{Q}\left(r_{b}-r_{a}\right)}{r_{b}}\)

Q” = \(\frac{\mathrm{Q} r_{a}}{r_{b}}\)

Question 46.
Select the correct pair of the following:
(a) Dipole moment and electric field
(b) Dipole moment and electric potential
(c) Electric permittivity and electric potential
(d) Electric pepnityivity and electric field
Answer:
(c) Electric permittivity and electric potential

Question 47.
Match the given quantities in both column J I and II: I

(a) (i) – (A); (ii) – (C); (iii) – (D); (iv) – (B)
(b) (i) – (D); (ii) – (B); (iii) – (E); (iv) – (C)
(c) (i) – (C); (ii) – (B); (iii) – (A); (iv) – (E)
(d) (i) – (E); (ii) – (D); (iii) – (B); (iv) – (A)
Answer:
(d) (i) – (E); (ii) – (D); (iii) – (B); (iv) – (A)

Question 48.
Which one of the following pairs’is a correct pair.
(a) Electric field and dielectric constant
(b) Electric field and dipole moment
(c) Electric flux and dielectric constant
(d) Electric potential and dielectric constant
Answer:
(b) Electric field and dipole moment
Hint:
They are vectors.

Question 49.
The effective capacitance of the following circuit is:

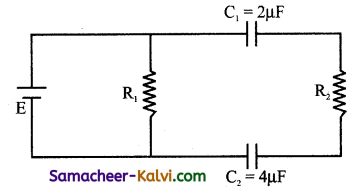
(a) \(\frac{3}{4}\) µF
(b) \(\frac{8}{3}\) µF
(c) \(\frac{4}{3}\) µF
(d) \(\frac{2}{3}\) µF
Answer:
(c) \(\frac{4}{3}\) µF
Hint:

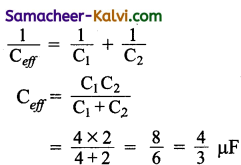
Question 50.
If a charge of q coulomb is placed at a point and a force F Newton is experienced by a unit positive charge then the electric field:
(a) E = \(\frac{\mathrm{F}}{q}\)

(b) E = \(\frac{q}{\mathrm{~F}}\)

(c) E = \(\frac{\mathrm{F}}{q^{2}}\)

(d) E = \(\frac{q^{2}}{\mathrm{~F}}\)
Answer:
(a) E = \(\frac{\mathrm{F}}{q}\)

Question 51.
Inverse square law enables to define unit of:
(a) charge
(b) positive charge
(c) electric field
(d) neutral charges
Answer:
(a) charge

Question 52.
The equation for permittivity of medium is:.
(a) ε = ε_r ε₀

(b) ε = \(\frac{\varepsilon_{0}}{\varepsilon_{r}}\)

(c) ε = \(\frac{\varepsilon_{r}}{\varepsilon_{0}}\)

(d) ε = ε_r – ε_o
Answer:
(a) ε = ε_r ε₀

Question 53.
Equation of electric charges is:
(a) q = ne
(b) q = Cv
(c) e = qn
(d) e = vC
Answer:
(a) q = me

Question 54.
The capacitance of a parallel plate capacitor increases from 5 µF to 60 µF when a dielectric is filled between the plates. The dielectric constant of the dielectric is:
(a) 65
(b) 55
(c) 12
(d) 10
Answer:
(c) 12
Hint:
ε_dielectric = \(\frac{\mathrm{C}_{\text {dielectric }}}{\mathrm{C}_{\text {air }}}\)

= \(\frac{60}{5}\) = 12

Question 55.
A hollow metal ball carrying an electric charge produces no electric field at points:
(a) outside the sphere
(b) on its surface
(c) inside the sphere
(d at a distance more than twice
Answer:
(c) inside the sphere

Question 56.
The electrostatic force between two point charges kept at a distance d apart, in a medium ε_r = 6, is 0.3 N. The force between them at the same separation in vacuum is:
(a) 20 N
(b) 0.5 N
(c) 1.8 N
(d) 2 N
Answer:
(c) 1.8 N

Question 57.
Electric field intensity is 400 V m^-1 at a distance of 2 m from a point charge. It will be 100 V m^-1 at a distance:
(a) 50 cm
(b) 4 cm
(c) 4 m
(d) 1.5 m
Answer:
(c) 4 m

Question 58.
Two point charges + 4q and +q are placed 30 cm apart. At what point on the line joining them the electric field is zero?
(a) 15 cm from the charge q
(b) 7.5 cm from the charge q
(c) 20 cm from the charge 4q
(d) 5 cm from the charge q
Answer:
(c) 20 cm from the charge 4q

Question 59.
The work done in moving 500 µC charge between two points on equipotential surface is:
(a) zero
(b) finite positive
(c) finite negative
(d) infinite
Answer:
(a) zero

Question 60.
The direction of electric field at a point on the equatorial line due to an electric dipole is:
(a) along the equatorial*line towards the dipole.
(b) along the equatorial line away from the dipole.
(c) parallel to the axis of the dipole and opposite to the direction of dipole moment.
(d) parallel to the axis of the dipole and in the direction of dipole moment.
Answer:
(c) parallel to the axis of the dipole and opposite to the direction of dipole moment.

Question 61.
The equivalent capacitance of two capacitors in series is 1.5 µF. The capacitance of one of them is 4 µF. The value of capacitance of the other is:
(a) 2.4 µF
(b) 0.24 µF
(c) 0.417 µF
(d) 4.17 µF
Answer:
(a) 2.4 µF
Hint:
\(\frac{1}{C_{s}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}\)

\(\frac{1}{1.5}=\frac{1}{4}+\frac{1}{c_{2}}\)

∴ C₂ = 24 µF

Question 62.
A hollow metallic spherical shell carrying an electric charge produces no electric field at points:
(a) on the surface of the sphere
(b) inside the sphere
(c) at infinite distance from the centre of the sphere
(d) outside the sphere
Answer:
(b) inside the sphere

Question 63.
Potential energy of two equal negative point charges of magnitude 2pC placed 1m apart in air is:
(a) 2 J
(b) 0.36 J
(c) 4 J
(d) 0.036 J
Answer:
(b) 0.36 J

Question 64.
The workdone in moving 4 µC charge from one point to another in an electric field is 0.012 J. The potential difference between them is:
(a) 3000 V
(b) 6000 V
(c) 30 V
(d) 48 × 10³ V
Answer:
(a) 3000 V

Question 65.
The total flux over a closed surface enclosing an electron is:
(a) 12.8 π × 10^-19
(b) 36 π × 10⁶
(c) 57.6 π × 10^-10
(d) 36 π × 10⁹
Answer:
(c) 57.6 π × 10^-10

Question 66.
The capacitance of a capacitor that should be connected along with two capacitors, having capcitances 4 µF and 8 µF all in series to produce effective capacitance of \(\frac{24}{11}\) µF is:
(a) 6 µF
(b) 2 µF
(c) 110 µF
(d) 12 µF
Answer:
(d) 12 µF
Hint:

Question 67.
When a number of capcitors of equal capacitances are connected in series, the effective capacitance is 0.4 µF and when they are connected in parallel, the effective capacitance is 90 µF. What is the capacitance Of each capacitor?
(a) 9 µF
(b) 10 µF
(c) 6 µF
(d) 3 µF
Answer:
(c) 6 µF
Hint:
C_s = \(\frac{c}{n}\) = 0.4 µF
C_p = nc = 90 µF
∴ C = 12 µF

Question 68.
The capacitance of a capacitor with a dielectric slab:
(a) decreases
(b) first decreases and then increases
(c) increases
(d) is infinity
Answer:
(c) increases

Question 69.
The capacitance of a capacitor, when a dielectric is introduced, is:
(a) \(\frac{\varepsilon_{r} \cdot \varepsilon_{0} \mathrm{~A}}{(d-t)+t}\)

(b) \(\frac{(d-t)+A}{\varepsilon_{0}+t / \varepsilon_{r}}\)

(c) \(\frac{\varepsilon_{0}(d-t)}{\mathrm{A}+t / \varepsilon_{r}}\)

(d) \(\frac{\varepsilon_{0} A}{(d-t)+t / \varepsilon_{r}}\)

Answer:
(d) \(\frac{\varepsilon_{0} A}{(d-t)+t / \varepsilon_{r}}\)

Question 70.
Two identical metal spheres have charges +15 µC and +25 µC and are separated by a distance. If the spheres are first brought into contact and then separated to the Original
distance, then the ratio of the. new force between them to the previous force is:
(a) 3 : 5
(b) 1 : 1
(c) 5 : 3
(d) 16 : 15
Answer:
(d) 16 : 15

Question 71.
Two charges + 4 C and + 1 C are separated by a distance of 3m. To keep these charges in equilibrium, a third charge is to be placed at:
(a) 2.5 m from the charge 1 C
(b) 1.5 m from the charge 4 C
(c) 2 m from the charge 4 C
(d) 2 m from the charge 1 C
Answer:
(c) 2 m from the charge 4 C

Question 72.
Two charges – q and + 2q are placed at A and B respectively. The distance between A and B is 12 m. At a point P between A and B, the potential is zero. Then, the distance of AP is:
(a) 3 m
(b) 4 m
(c) 6 m
(d) 8 m
Answer:
(b) 4 m

Question 73.
If two capacitors of capacitances 2 µF and 4 µF are connected in parallel, the effective capacitance of the system is:
(a) 6 µF
(b) \(\frac{3}{4}\) µF
(c) \(\frac{4}{3}\) µF
(d) 2 µF
Answer:
(a) 6 µF

Question 74.
If two capacitors of capacitances 2 µF and 6 µF are put in series, the effective capacitance of the system is:
(a) 8 µF
(b) 2 µF
(c) \(\frac{3}{2}\) µF
(d) \(\frac{2}{3}\) µF
Answer:
(d) \(\frac{2}{3}\) µF

Question 75.
Two capacitors each of 4 µF capacitance are joined in parallel. The effective capacitance is:
(a) 4 µF
(b) 8 µF
(c) 2 µF
(d) 6 µF
Ans :
(b) 8 µF

Question 76.
The leakage of electric charge from the sharp points on a charged conductor is known as:
(a) action of points
(b) electric field strength
(c) electric potential
(d) electrostatic induction
Answer:
(a) action of points

Question 77.
What is the use of Van de Graaff generator?
(a) To produce very high voltage
(b) To produce high current
(c) To produce high electric field strength
(d) To produce high electric power
Answer:
(a) To produce very high voltage

Question 78.
Select the correct pair of polar molecules:
(a) H₂O and H₂
(b) HCl and O₂
(c) CO₂ and NH₃
(d) HCl and NH₃
Answer:
(d) HCl and NH₃

Question 79.
Choose the odd man out from the following:
(a)N₂O
(b) CO₂
(c) HCl
(d) H₂O
Answer:
(b) CO₂

Question 80.
Select correct pair of the following j non – polar molecules:
(a) H₂ and HCl
(b) O₂ and CO₂
(c) O₂ and N₂O
(d) CO₂ and NH₃
Answer:
(b) O₂ and CO₂

Question 81.
Match the following quantities in Column I ! with the given quantities in Column II.

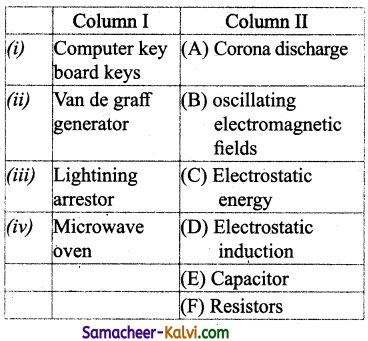
(a) (i) – (E); (ii) – (D); (iii) – (A); (iv) – (B)
(b) (i) – (C); (ii) – (B); (iii) – (D); (iv) – (A)
(c) (i) – (F); (ii) – (E); (iii) – (D); (iv) – (C)
(d) (i) – (E); (ii) – (D); (iii) – (A); (iv) – (B)
Answer:
(d) (i) – (E); (ii) – (D); (iii) – (A); (iv) – (B)

Question 82.
Choose the correct statements from the following for the given situation.
The dielectric can be inserted into the plates of a capacitor when,
(i) the capacitor is connected to the battery
(ii) the capacitor is disconnected from the battery
(iii) the capacitor is discharging and plates are removed
(iv) the capacitor is charging without the j plates
(a) (i) and (iii)
(b) (i) and (iv)
(c) (ii) and (iii)
(d) (i) and (ii)
Answer:
(d) (i) and (ii)

Question 83.
Match the quantities given in Column I and II:

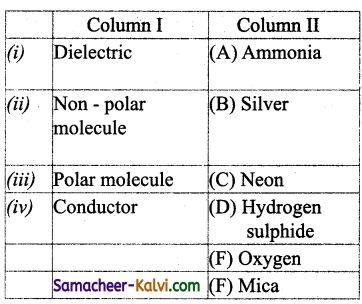
(a) (i) – (D); (ii) – (A); (iii) – (C); (iv) – (F)
(b) (i) – (E); (ii) – (D); (iii) – (B); (iv) – (A)
(c) (i) – (A); (ii) – (B); (iii) – (C); (iv) – (F)
(d) (i) – (F); (ii) – (E); (iii) – (A); (iv) – (B)
Answer:
(d) (i) – (F); (ii) – (E); (iii) – (A); (iv) – (B)

Question 84.
Match the following quantities given in Column I and Column II.

(a) (i) – (A); (ii) – (F); (iii) – (B); (iv) – (D)
(b) (i) – (B); (ii) – (C); (iii) – (E); (iv) – (D)
(c) (i) – (F); (ii) – (E); (iii) – (A); (iv) – (C)
(d) (i) – (E); (ii) – (F); (iii) – (A); (iv) – (C)
Answer:
(d) (i) – (E); (ii) – (F); (iii) – (A); (iv) – (C)

Question 85.
The electric field intensity due to n cylinders having charge q per unit length and radius R at a distance r that is greater than R from its j axis is:
(a) directly proportional to r
(b) directly proportional to r²
(c) inversely proportional to r
(d) inversely proportional to r²
Answer:
(c) inversely proportional to r
Hint:
By Gauss law
Φ × E ds = \(\frac{q l}{\varepsilon_{0}}\)
When E is constant
Φ . E ds = E × 2 π rl
∴ E × 2 π rl = \(\frac{q }{\varepsilon_{0}}\) l

∴ E = \(\frac{q}{2 \pi \varepsilon_{0} r}\)

∴ E ∝ \(\frac{1}{r}\)

TN Board 12th Physics Important Questions