TN State Board 12th Physics Important Questions Chapter 3 Magnetism and Magnetic Effects of Electric Current
Question 1.
Which quantities are required to specify the magnetic field of the Earth?
Answer:
(i) Magnetic declination (D)
(ii) Magnetic dip or inclination (I) and
(iii) The horizontal component of the Earth’s magnetic field BH.
Question 2.
What is meant by magnetic declination?
Answer:
Magnetic declination is the angle between magnetic meridian at a point and geographical meridian.
Question 3.
What is dip or magnetic inclination?
Answer:
Magnetic inclination or dip is the angle subtended by the Earth’s total magnetic field \(\vec{B}\) with the horizontal direction in the magnetic meridian.
![]()
Question 4.
Where will the horizontal component of earth’s magnetic field be
(i) maximum and
(ii) minimum?
Answer:
The horizontal component of earth’s magnetic field will be –
(i) Maximum at equator.
(ii) Minimum (zero) at poles.
Question 5.
At (i) equator and (ii) poles what will be vertical component of Earth’s magnetic field?
Answer:
The vertical component of Earth’s magnetic field will be
(i) minimum (zero) at equator
(ii) maximum at poles
Question 6.
What is meant by magnetic field?
Answer:
Magnetic field is the region or space around energy magnet within which its influence can be felt by keeping another magnet in that region.
![]()
Question 7.
What are the unit and dimension of magnetic flux?
Answer:
Unit of magnetic flux is Weber.
Dimension of magnetic flux is M L2 T-2 A-1.
Question 8.
State the unit and dimension of magnetic flux density.
Answer:
Unit of magnetic flux density is Wb m-2 or Tesla
Dimension of magnetic flux density [ML° T-2 A-1].
Question 9.
State the unit dimension of pole strength.
Answer:
Unit of pole strength is newton per Tesla or ampere-metre.
Dimension of pole strength is [M°L T° A]
![]()
Question 10.
Define magnetic pole.
Answer:
A magnetic pole is defined as that pole which when placed at a distance of 1 metre in air from an equal and similar pole repels with a force of 10-7 N.
Question 11.
What is the value of permeability of free space?
Answer:
Value of permeability of free space is
µ0 = 4π × 10-7 Henry /metre.
Question 12.
What is the nature of magnetic susceptibility?
Answer:
Magnetic susceptibility is a scalar. It is a scalar for isotropic medium. It is a tensor for non-isotropic medium.
![]()
Question 13.
State examples for diamagnetic substances.
Answer:
Bismith, Copper and Water etc.
Question 14.
Mention examples for paramagnetic materials.
Answer:
Aluminium, Platinum, and Chromium etc.
Question 15.
State the relation between relative permeability and susceptibility.
Answer:
The relation is given by µr = 1 + k
µ0 – relative permeability and k – susceptibility
Question 16.
How are the values of relative permeability for dia, para and ferro magnetic materials different?
Answer:
For a diamagnetic material, the relative permeability is less than one µr < 1.
For paramagnetic substances the relative permeability is slightly greater than one, µr > 1
For ferromagnetic materials µr >> 1;
For pure iron µr = 2,00,000.
![]()
Question 17.
State examples for ferromagnets.
Answer:
Iron, Nickel and Cobalt.
Question 18.
How can a galvanometer be converted into an ammeter?
Answer:
A galvanometer is transformed into an ammeter by connecting a low resistance in parallel with the galvanometer.
Question 19.
Why is ammeter always to be connected in series?
Answer:
The ammeter must offer low resistance such that it will not change the current passing through it. So ammeter is connected in series to measure the circuit current.
Question 20.
How is galvanometer converted into voltmeter?
Answer:
A galvanometer is transformed into a voltmeter by connecting high resistance Rh in series with galvanometer.
![]()
Question 21.
Voltmeter is always connected in series. Give reason.
Answer:
Voltmeter must have high resistance and when it is connected in parallel, it will not draw appreciable current. So that it will indicate the true potential difference. So, voltmeter is always connected in series.
Question 22.
Define magnetic field at a point.
Answer:
Magnetic field at a point is defined as the force experienced by the bar magnet of unit pole strength.
Question 23.
What are artificial magnets?
Answer:
Artificial magnets are magnets that are made by human in order to have desired shape and strength.
Eg: Bar magnets.
![]()
Question 24.
What are magnetic field lines?
Answer:
Magnetic field lines are continuous closed curves. They never intersect each other.
Question 25.
What is meant by magnetic flux?
Answer:
Magnetic flux ΦB is the number of magnetic field lines crossing per unit area.
ΦB = \(\overrightarrow{\text { B }} \cdot \vec{A}\) = BA cos θ
Question 26.
Define Magnetic flux density.
Answer:
Magnetic flux density is defined as the number of magnetic field lines crossing unit area kept normal to the direction of line of force.
Question 27.
When will be the magnetic field said to be uniform? State an example.
Answer:
A magnetic field is said to be uniform, if it has same magnitude and direction at all the points in a given region.
Eg: Local Earth’s magnetic field.
![]()
Question 28.
What is meant by non-uniform magnetic field?
Answer:
In a non-uniform magnetic field, the magnitude or direction or both varies at all its points.
Eg: Magnetic field of a bar magnet.
Question 29.
Why does a freely suspended bar magnet experience only torque in the laboratory?
Answer:
It is because Earth’s magnetic field is locally (laboratory) minimum.
Question 30.
When will the potential energy of a bar magnet be maximum and minimum?
Answer:
The potential energy of a bar magnet will be maximum when the bar magnet is aligned anti-parallel to external magnetic field.
It will be minimum when the bar magnet is aligned along the external magnetic field.
![]()
Question 31.
State Tangent law.
Answer:
When a magnetic needle or magnet is freely suspended in two mutually perpendicular uniform magnetic fields, it will come to rest, in the direction of the resultant of two magnetic fields.
Question 32.
What is meant by magnetising field?
Answer:
The magnetising field is a’magnetic field that magnetizes a specimen kept in that magnetic field.
Question 33.
Define Magnetic permeability.
Answer:
Magnetic permeability is defined as the measure of ability of the material to allow the passage of magnetic field lines through it.
![]()
Question 34.
Define relative permeability.
Answer:
Relative permeability is defined as the ratio between the absolute permeability of the medium to the permeability of free space.
Question 35.
What is meant by intensity of magnetisation?
Answer:
The net magnetic moment per unit volume of material is known as intensity of magnetisation.
M = Magnetic moment / Volume
M = \(\frac{\vec{p}_{m}}{\mathrm{~V}}\)
Question 36.
Derive the relation between total magnetic field (B) and magnetising field H.
Answer:
Let total magnetic field be \(\vec{B}\)
Let magnetic field produced in vacuum be B0
Let magnetic field due to magnetisation be \(\overrightarrow{\mathbf{B}}_{m}\)
Then \overrightarrow{\mathbf{B}}=\mathbf{\mathbf { B }}_{0}+\overrightarrow{\mathbf{B}}_{m}
= µ0 \(\vec{H}\) + µ0I
= µ0 (\(\vec{H}\) + \(\vec{I}\))
![]()
Question 37.
Two substances A and B have their relative permeabilities slightly greater than and slightly less than unity respectively. To which group do A and B belong?
Answer:
The relative permeability of A is greatef than unity. Therefore, it is a paramagnetic substance. The relative permeability of B is less than unity. Therefore, it is a diamagnetic substance.
Question 38.
What is curie temperature?
Answer:
When a ferro-magnetic material is heated it loses its ferro magnetism slowly and at a particular temperature ferromagnetism vanishes and the material just becomes paramagnetic. This temperature is called the curie temperature. For example, curie temperature of iron about 1000 K.
Question 39.
State Curie’s law.
Curie’s law states that Susceptibility of a magnetic material is inversely proportional to absolute temperature.
χm ∝ \(\frac{1}{\mathrm{~T}}\)
χm = \(\frac{\mathrm{C}}{\mathrm{T}}\)
![]()
Question 40.
Draw a graph to show the variation of magnetic susceptibility with absolute temperature.
Answer:
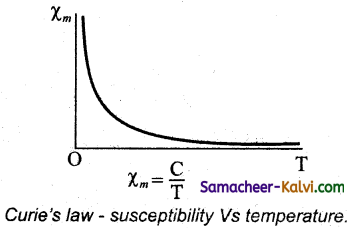
Question 41.
Write the mathematical form forcurie-Weiss law.
Answer:
Curie Weiss law is given in the mathematical forms as
χm = \(\frac{C}{T-T_{C}}\)
when,
C – Curie Constant
T – Temperature in kelvin
Tc – Curie temperature
Question 42.
Mention the graphical representation of Curie – Weiss law.
Answer:
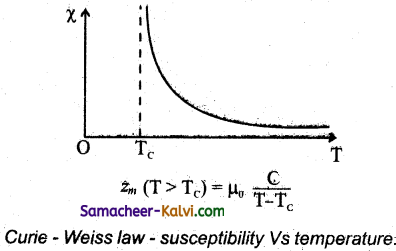
![]()
Question 43.
How can the loss of heat energy per unit temperature of iron is about 1000 K. 1 volume be calculated during hysteresis?
Answer:
It has been found that loss of heat energy per unit volume of the specimen in each Cycle of magnetisation is equal to the area of the hysteresis loop.
Question 44.
What is the use of studying hysteresis loops of various materials?
Answer:
The shape and size of the hysteresis loop is characteristic of each material because of the differences in their retentivity, coercivity, permeability, susceptibility and energy less, etc., By studying hysteresis loops of various materials, One can select suitable materials for different purposes.
Question 45.
Derive the relation between χm and µr.
Answer:
χm = \(\frac{\mathrm{I}}{\mathrm{H}}\)
∴ I = χmH
We know B = µ0 (H + I)
B = µ0 (H + χmH)
B = µ0H (I + χm)
If µ is the permeability, we know that
B = µH.
∴ µH = µ0H (l + χm)
\(\frac{\mu}{\mu_{0}}\) = (l + χm)
∴ µr = (l + χm)
![]()
Question 46.
Explain with the help of the domain theory ferromagnetic behaviour of materials.
Answer:
Ferromagnetism is not an atomic property but just a special arrangement of groups of atoms into magnetic domains which are magnetised *to saturation. These are of size (1 – 0.1 mm across). These domains exist throughout the ferromagnetic substance. Bach domain is associated with a strong magnetic moment.
Question 47.
Define retentivity.
Answer:
Retentivity is defined as the ability of the material to retain the magnetism in them even magnetising field vanishes.
Question 48.
Compare the hysteresis loops for two magnetic materials. Comparison of two ferromagnetic material –
Answer:
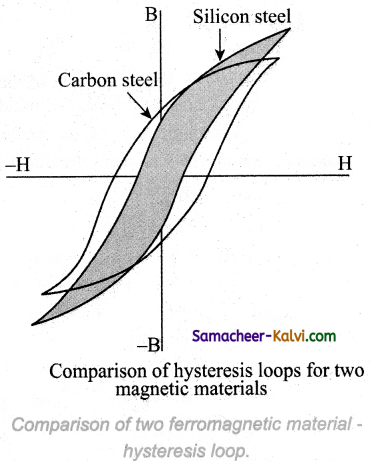
![]()
Question 49.
What is Coercivity?
Answer:
Coercivity is the magnitude of the reverse magnetising field for which the residual magnetism of the material vanishes.
Question 50.
What are the properties of ferromagnetic materials that can be used to manufacture permanent magnets?
Answer:
The ideal material for making permanent magnets should possess high retentivity (residual magnetism) and high coercivity so that the magnetisation lasts for a longer time. Examples of such substances are steel and alnico (an alloy of Al, Ni and Co).
Question 51.
Why is soft iron “preferred for making electromagnets?
Answer:
Soft iron is preferred for making electromagnets as it has a thin hysteresis loop, (small area, therefore less hysteresis loss) and low retentivity. It attains high values of B at low values of magnetising field H.
![]()
Question 52.
State right hand thumb rule.
Answer:
Right hand thumb rule states that “If we hold the current carrying conductor in our encircling the wire points in the direction of the magnetic field lines produced.
Question 53.
Explain the use of ferromagnetic materials in a modern computer.
Answer:
Ferromagnetic materials are used for coating magnetic tapes in a cassette player and for building a memory store in a modem computer.
Ferrites (Fe, Fe2O, MnFe2O4 etc..)
Question 54.
State Maxwell’s right hand cork screw rule.
Answer:
It states that if we rotate a right-handed screw by a screw driver, then the direction of current is same as the direction in which screw advances and the direction of the screw gives the direction of magnetic field.
![]()
Question 55.
Distinguish electric field from magnetic field.
Answer:
| Electric field | Magnetic field |
| Produced by a scalar source i.e., an electric charge q | Produced by a vector source i.e., current element I \(d \vec{l}\) |
| It is directed along the position vector joining the source and the point at which the field is calculated | It is directed perpendicular to the position vector r and the current element I\(d \vec{l}\) |
| Does not depend on angle. | Depends on the angle between the position vector \(\vec{r}\) and the current element I \(d \vec{l}\) |
Question 56.
State similarities between Coulomb’s law and Biot Savart’s law.
Answer:
Electric and magnetic fields
- Obey inverse square law, so they are long range fields.
- Obey the principle of superposition and are linear with respect to source. In magnitude,
- E ∝ q
B ∝ Idl .
Question 57.
Mention right hand thumb rule.
Answer:
If we curl the fingers of right hand in the direction of current in the loop, then the stretched thumb gives the direction of the magnetic moment associated with the loop.
Question 58.
What is toroid?
Answer:
If we bent a solenoid in a way that both their ends are joined together to form a closed ring shape then it is called a toroid.
![]()
Question 59.
Define Tesla.
Answer:
The strength of the magnetic field is one tesla if unit charge moving in it with unit velocity experiences unit force.
1 T = \(\frac{1 \mathrm{Ns}}{\mathrm{Cm}}\)
= 1 \(\frac{\mathrm{N}}{\mathrm{Cm}}\)
= 1NA-1m-1
Question 60.
What is Bohr Magneton?
Answer:
The minimum value of magnetic moment of a revolving electron is eh
(µ1)min = \(\frac{e h}{4 \pi m}\), n = 1
The value of \(\frac{e h}{4 \pi m}\) is called Bohr magneton.
By substituting the values of e, h and m, the value of Bohr magneton is found to be 9.27 × 10-24 Am2.
Question 61.
Define magnetic moment of a current loop.
Answer:
The magnetic moment of a current loop is defined as the product of the current and the loop area. Its direction is perpendicular to the plane of the loop.
![]()
Question 62.
State Right hand palm rule.
Answer:
The coil is held in the right hand so that the fingers point in the direction of the current in the windings. The extended thumb, points in the direction of the magnetic field.
Question 63.
State limitations of cyclotron.
Answer:
(i) the speed of the ion is limited
(ii) electron cannot be accelerated
(iii) uncharged particles cannot be accelerated
Question 64.
State Fleming’s left hand rule.
Answer:
Fleming’s left hand rule states that stretch forefinger, the middle finger and the thumb of the left hand such that they are in mutually perpendicular directions. If forefinger points the direction of magnetic field, the middle finger points the direction of the electric current, then thumb will point the direction of the force experienced by the conductor.
Question 65.
Define ampere.
Answer:
One ampere is defined as that current when it is passed through each of the two infinitely long parallel straight conductors kept at a distance of one meter apart in vacuum causes each conductor to experience a force of 2 × 10-7 newton per meter length of conductor.
![]()
Question 66.
Define figure of merit of a galvanometer.
Answer:
Figure of merit of a galvanometer, is defined as the current which produces a deflection of one scale division in the galvanometer.
Question 67.
Define current sensitivity.
Answer:
Current sensitivity, is defined as the deflection produced per unit current flowing through it. 0
Is = \(\frac{\theta}{I}\)
= \(\frac{\mathrm{NAB}}{\mathrm{K}}\)
⇒ Is = \(\frac{\mathrm{I}}{\mathrm{G}}\)
Question 68.
How can be the current sensitivity of a galvanometer increased?
Answer:
The current sensitivity of a galvanometer can be increased
(a) by increasing
- the number of turns N
- the magnetic induction B
- the area of the coil A
(b) by decreasing
the couple per unit twist of the suspension.
![]()
Question 69.
Why phosphor bronze wire is used as suspension wire in moving coil galvanometer?
Answer:
Phosphor bronze wire will produce small couple per unit twist. So current sensitivity of a galvanometer will be increased. Hence phosphor bronze wire is used as suspension ” wire in moving coil galvanometer.
Question 70.
In galvanometer, increasing the current sensitivity does not necessarily increase the voltage sensitivity. Explain.
Answer:
Increasing the current sensitivity does not necessarily, increase the voltage sensitivity. When the number of turns (n) is doubled, current sensitivity is also doubled. But increasing the number of turns correspondingly increases the resistance (G). Hence voltage sensitivity remains unchanged.
Question 71.
Define Voltage Sensitivity.
Answer:
Voltage sensitivity, is defined as the deflection produced per unit voltage applied across it.
Vs = \(\frac{\theta}{\mathrm{V}}\)
Vs = \(\frac{\theta}{\mathrm{IR}_{g}}\) = \(\frac{\mathrm{NAB}}{\mathrm{KR}_{g}}\)
Vs = \(\frac{1}{\mathrm{GR}_{g}}\) = \(\frac{\mathrm{I}_{\mathrm{S}}}{\mathrm{R}_{g}}\)
where Rg is the resistance of galvanometer.
![]()
Question 72.
Write a note on pointer type moving coil galvanometer.
Answer:
Pointer type moving coil galvanometer:
The suspended coil galvanometers are very sensitive. They can measure current of the order of 10-8 ampere. Hence these galvanometers have to be carefully handled. So, in the laboratory, for experiments like Wheatstone’s bridge, where sensitivity is not required, pointer type galvanometers are used. In this type of galvanometer, the coil is pivoted on ball bearings. A lighter aliminium pointer attached to the coil moves over a scale when current is passed. The restoring couple is provided by a spring.
Question 73.
Distinguish ammeter from voltmeter.
Answer:
| Ammeter | Voltmeter |
| It is low resistance instrument. | It is a high resistance instrument. |
| It is always connected in series. | It is always connected in parallel. |
| An ideal ammeter has zero resistance | An ideal voltmeter has infinite resistance. |
![]()
Question 74.
Explain the basic properties of magnets with the help of diagrams.
Answer:
(a) Magnetic dipole moment:
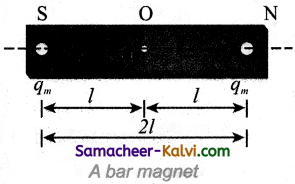
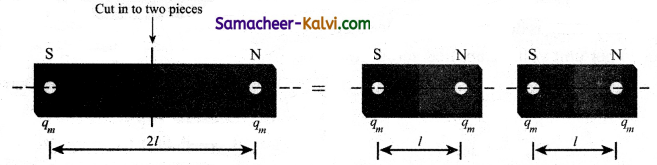
Let us consider a bar magnet. Let qm be the pole strength (it is also called as magnetic charge) of the magnetic pole and let / be the distance between the geometrical centre of bar magnet O and one end of the pole. The magnetic dipole moment is defined as the product of its pole strength and magnetic length It is a vector quantity, denoted by pm.
\(\vec{p}_{m}=q_{m} \vec{d}\) ………..(1)
where \(\vec{B}\) is the vector drawn from South pole to North pole and its magnitude \(|\vec{d}|\) = 2l
The magnitude of magnetic dipole moment is pm = 2qml.
The SI unit of magnetic moment is Am2. It is noted that the direction of magnetic moment is from South pole to North pole.
(b) Magnetic field:
Magnetic field is the region or space around every magnet within which its influence can be felt by keeping another magnet in that region. The magnetic field \(\vec{B}\) at a point is defined as a force experienced by the bar magnet of unit pole strength.
\(\overrightarrow{\mathrm{B}}=\frac{1}{q_{m}} \overrightarrow{\mathrm{F}}\) ………..(2)
Its unit is N A-1 m-1.
(c) Types of magnets:
Magnets are classified into natural magnets and artificial magnets. For example, iron, cobalt, nickel, etc., are natural magnets. Strengths of natural magnets are very weak and the shapes of the magnet are irregular. Artificial magnets are made by us in order to have desired shape and strength Bar magnet is a magnet that exist in the form of rectangular shape or cylindrical shape.
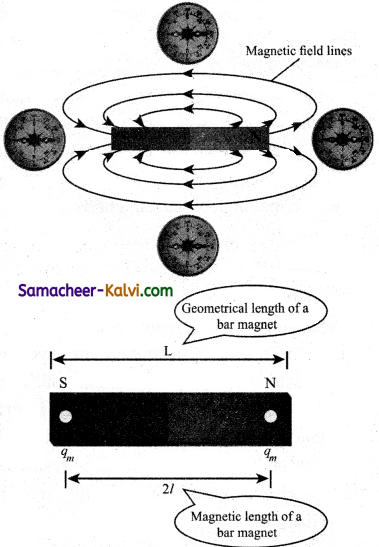
Properties of bar magnet:
The following are the properties of bar magnet:
(i) A freely suspended bar magnet will always point along the north-south direction. .
(ii) A magnet attracts another magnet or magnetic substances towards itself. The attractive force is maximum near the end of the bar magnet. When a bar magnet is dipped into iron filling, they cling to the ends of the magnet.
(iii) When a magnet is broken into pieces, each piece behaves like a magnet with poles at its ends.
(iv) Two poles of magnet have pole strength equal to one another.
(v) The length of the bar magnet is called geometrical length and the length between two magnetic poles in a bar magnet is called magnetic length. Magnetic length is always slightly smaller than geometrical length. The ratio of magnetic length and geometrical length is \(\frac{5}{6}\)
\(\frac{\text { Magnetic length }}{\text { Geometricál length }}=\frac{5}{6}\) = 0.833.
![]()
Question 75.
Mention the properties of magnetic lines.
Answer:
(i) Magnetic field lines are continuous closed curves. The direction of magnetic field lines is from North pole to South pole outside the magnet and South pole to North pole inside the magnet.
(ii) The direction of magnetic field at any point on the curve is found by drawing tangent to the magnetic line of force at that point. In the tangent drawn at points P, Question and R gives the direction of magnetic field B at that point.
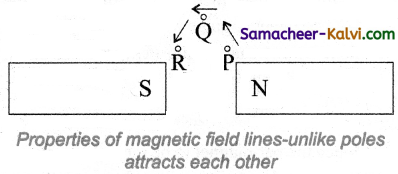
(iii) Magnetic field lines never intersect each other. Otherwise, the magnetic compass needle would point towards two directions, that is impossible.
(iv) The degree of closeness of the field lines determines the relative strength of the magnetic field. The magnetic field is strong where magnetic field lines crowd and weak where magnetic field lines thin out.
Question 76.
Describe principle construction and theory of a Tangent galvanometer.
Answer:
When a magnetic needle or magnet is freely suspended in two piutually perpendicular uniform magnetic fields, it will come to rest in the direction of the resultant of the two fields.
B = BH tan θ ………(1)
Construction:
Tangent Galvanometer (TG) consists of copper coil wounded on a non-magnetic circular frame. The frame is made up of brass or wood which is mounted vertically on a horizontal base table (turn table) with three levelling screws. The TG is provided with two or more coils of different number of turns. Most of the equipments consist of 2 turns, 5 turns and 50 turns which are of different thickness and are used for measuring currents of different strength.
At the centre of turn table, a small upright projection is seen on which compass box is placed. Compass box consists of a small magnetic needle which is pivoted at the centre, such that arrangement shows the centre of both magnetic needle and circular coil exactly coincide. A thin aluminium pointer is connected to the magnetic needle normally and moves over circular scale.
The circular scale is divided into four quadrants and graduated in degrees those are used to measure the deflection of aluminium pointer on a circular degree scale. In order to avoid parallax error in measurement, a mirror is placed below the aluminium pointer.
Theory:
The circuit connection for Tangent Galvanometer (TG) experiment. When no current is passed through the coil, the small magnetic needle lies along horizontal component of Earth’s magnetic field. When the circuit is switched ON, the electric current will pass through the circular coil and produce magnetic field. Now there are two fields which are acting mutually perpendicular to each other. They are:
(i) the magnetic field (B) due to the electric current in the coil acting normal to the plane of the coil.
(ii) the horizontal component of Earth’s magnetic field (BH)
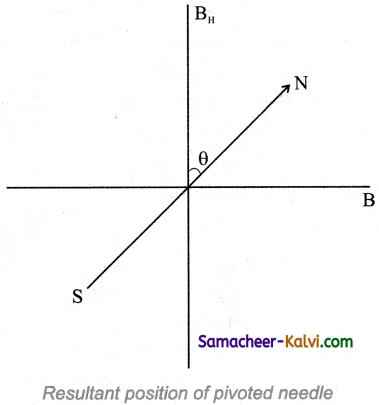
Because of these crossed fields, the pivoted magnetic needle deflects through an angle θ. From tangent law,
B = BH tan θ
It is known that when an electric current is passed through a circular coil of radius R having N turns, the magnitude of magnetic field at the centre is
B = µ0 \(\frac{\mathrm{NI}}{2 \mathrm{R}}\) ………. (2)
From equation (1) and equation (2), we get
µ0 \(\frac{\mathrm{NI}}{2 \mathrm{R}}\) = BH tan θ
The horizontal component of Earth’s magnetic field can be determined as NT 1
BH = µ0 \(\frac{N I}{2 R} \frac{1}{\tan \theta}\) in tesla ………. (3)
![]()
Question 77.
A bar magnet it placed in a uniforn magnetic field. Obtain an expression for potential | energy of the magnet.
Answer:
When a bar magnet (magnetic dipole) of dipole moment \(\vec{p}_{m}\) is held at an angle θ with the direction of a uniform magnetic field B, the magnitude of the torque acting on the dipole is given by
\(\left|\vec{\tau}_{\mathrm{B}}\right|=\left|\vec{p}_{m}\right||\overrightarrow{\mathrm{B}}| \sin \theta\)
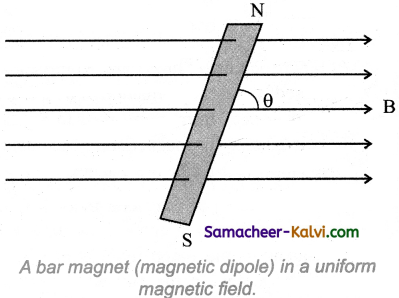
If the dipole is rotated through a very small angular displacement dQuestion against the torque xB at constant angular velocity, then the work done by external torque (Xext) for this small angular displacement is
dW = \(\left|\vec{\tau}_{\text {ext }}\right|\)dQ
Since the bar magnet to be moved at constant angular velocity, it implies
dW = pm B sinθ dθ
Total work done in rotating the dipole from θ’ to θ is
W = \(\int_{\theta^{\prime}}^{\theta}\) τ dθ
= \(\int_{\theta^{\prime}}^{\theta}\) pm B sin θ dθ
= pm B\([-\cos \theta d \theta]_{\theta^{\prime}}^{\theta}\)
W = – pm B (cos θ – cos θ’)
This work done is stored as potential energy in bar magnet at an angle θ when it is rotated from θ’ to θ and it can be written as
U = – pmB(cos θ – cos θ’)
In fact, the above equation above gives the difference in potential energy between the angular position θ’ and θ. We can select the reference point θ’ = 90°, so that second term in the equation becomes zero and the equation above can be written as
U = -pm B(cos θ)
The potential energy stored in a bar magnet in a uniform magnetic field is given by
U = \(\vec{p}_{m} \cdot \overrightarrow{\mathrm{B}}\)
Case (i):
If θ = 0°, then
U = – pm B (cos 0°) = – pm B
Case (ii):
If θ = 180°, then
U = – pm B (cos 180°) = pm B
It is inferred from the above two results, the potential energy of the bar magnet is minimum when it is aligned along the external magnetic field and maximum when the bar magnet is aligned anti-parallel to external magnetic field.
![]()
Question 78.
State the properties of diamagnetic materials.
Answer:
(i) Magnetic susceptibility is negative.
(ii) Relative permeability is slightly less than unity.
(iii) The magnetic field lines are repelled or expelled from diamagnetic materials when they are placed in a magnetic field.
(iv) Susceptibility is nearly, temperature independent.
Question 79.
Mention the properties of paramagnetic.
Answer:
(i) Magnetic susceptibility of a paramagnet is positive and small.
(ii) It’s relative permeability is greater than unity.
(iii) The magnetic field lines are attracted into the paramagnetic materials when they are placed in a magnetic field.
(iv) Susceptibility is inversely proportional to the temperature.
Question 80.
What are the properties of ferromagnetic materials?
Answer:
(i) Magnetic susceptibility of ferromagnets is positive and large.
(ii) It’s relative permeability is large.
(iii) The magnetic field lines are strongly attracted into the ferromagnetic materials when placed in a magnetic field.
(iv) Susceptibility is inversely proportional to the temperature.
![]()
Question 81.
With the help of a diagram explain hysteresis loop.
Answer:
A ferromagnetic material (example, Iron) is magnetised slowly by a magnetising field \(\vec{H}\). The magnetic induction \(\vec{B}\) of the material increases from point A with the magnitude of the magnetising field and then attains a saturated level. This behaviour of the material is depicted by the path AC. Saturation magnetization is defined as the maximum point up to which the material can be magnetised by applying the magnetising field.
If the magnetising field is now reduced, the magnetic induction also decreases but does not retrace the original path CA. It takes different path CD. When the magnetising field is zero, the magnetic induction is not zero and it has positive value. It is implied that some magnetism is left in the specimen. The residual magnetism AD present in the specimen is called remanence or retentivity. It is defined as the ability of the materials to retain the magnetism in them even magnetising field vanishes.
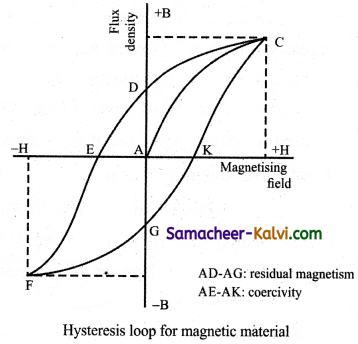
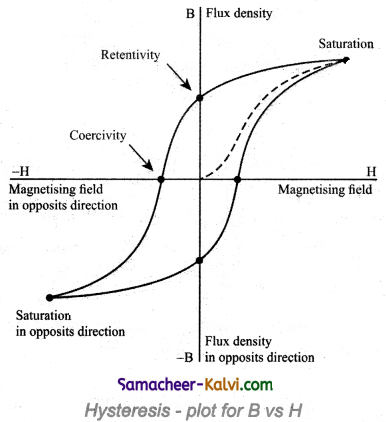
In order to demagnetise the material, the magnetising field is gradually increased in the reverse direction. Now the magnetic induction decreases along DE and becomes zero at E. The magnetising field AE in the reverse direction is required to bring residual magnetism to zero. The magnitude of the reverse magnetising field for which the residual magnetism of the material vanishes is called its coercivity.
Further increase of \(\vec{H}\) in the reverse direction, the magnetic induction increases along EF until it reaches saturation at F in the reverse direction. If magnetising field is decreased and then increased with direction reversed, the magnetic induction traces the path FGKC. This closed curve ACDEFGK is called hysteresis loop and it represents a cycle of magnetisation.
In the entire cycle, the magnetic induction B lags behind the magnetising field H. This phenomenon of lagging of magnetic induction behind the magnetising field is called hysteresis.
![]()
Question 82.
Explain applications of hysteresis loop with illustrations.
Answer:
The significance of hysteresis loop is that it provides information such as retentivity, coercivity, permeability, susceptibility and energy loss during one cycle of magnetisation for each ferromagnetic material. Therefore, the study of hysteresis loop will help us in selecting proper and suitable material for a given purpose.
Illustrations:
(i) Permanent magnets:
The materials with high retentivity, high coercivity and high permeability are suitable for making permanent magnets.
Eg: Steel and Alnico
(ii) Electromagnets:
The materials with high initial permeability, low retentivity, low coercivity and thin hysteresis loop with smaller area are preferred to make electromagnets.
Eg; Soft iron and Mumetal (Nickel Iron alloy).
(iii) Core of the transformer:
The materials with high initial permeability, large magnetic induction and thin hysteresis loop with smaller area are needed to design transformer cores.
Eg: Soft iron
Question 83.
Derive the relation between angular momentum and magnetic moment of an electron.
Answer:
Suppose an electron undergoes circular motion around the nucleus. The circulating electron in a loop is like current in a circular loop (since flow of charge is known as current). The magnetic dipole moment due to current carrying circular loop is
\(\vec{\mu}_{\mathrm{L}}=\mathrm{I} \overrightarrow{\mathrm{A}}\) ………………(1)
In magnitude,
µL = IA
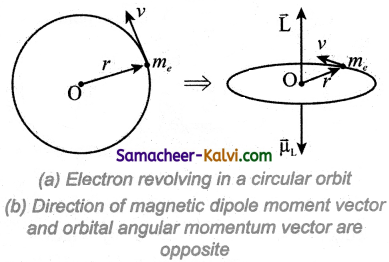
If T is the time period of an electron, the current due to circular motion of the electron is
I = \(\frac{-e}{\mathrm{~T}}\) ………….(2)
where -e is the charge of an electron. If R is the radius of the circular orbit and v is the velocity of the electron in the circular orbit, then
T = \(\frac{2 \pi R}{v}\) ………….(3)
Using equation (2) and equation (3) in equation (1), we get
µL = \(-\frac{e}{\frac{2 \pi R}{v}} \pi R^{2}=-\frac{e v R}{2}\) ……….(4)
where A = πR2 is the area of the circular loop.
By definition, angular momentum of the electron about O is
\(\overrightarrow{\mathrm{L}}=\vec{r} \times \vec{p}\)
In magnitude,
L = Rp = mvR ……………(5)
Using the above equations (4) and (5), we get
⇒ \(\vec{\mu}_{\mathrm{L}}=-\frac{e}{2 m} \overrightarrow{\mathrm{L}}\) ……………..(6)
It is indicated that the magnetic moment and angular momentum are n opposite direction from the negative sign.
In magnitude,
\(\frac{\mu_{\mathrm{L}}}{\mathrm{L}}=\frac{e}{2 m}=\frac{1.60 \times 10^{-19}}{2 \times 9.11 \times 10^{-31}}\)
= 0.0878 × 1012
\(\frac{\mu_{\mathrm{L}}}{\mathrm{L}}\) = 8.78 × 1010 Ckg-1 = Constant
The ratio \(\frac{\mu_{\mathrm{L}}}{\mathrm{L}}\) is a constant and also known as gyro-magnetic ratio . \(\left(\frac{e}{2 m}\right)\). that the gyro-magnetic ratio is a constant of proportionality which connects angular momentum of the electron and the magnetic moment of the electron.
![]()
Question 84.
Obtain exf ions for the magnetic field of a toroid.
Answer:
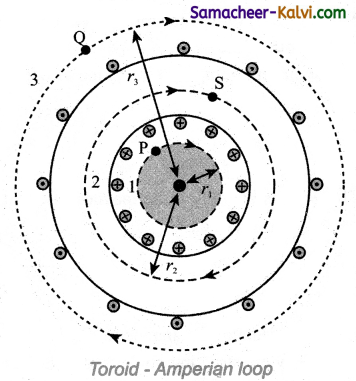
(a) Open space interior to the toroid:
Let us calculate the magnetic field B at point P. We construct an Amperian loop 1 of radius r1 around the point P. For simplicity, we take circular ioop so that the length of the loop is its circumference.
L1 = 2πr1
Ampere’s circuital law for the loop 1 is
Since, the loop 1 encloses no current,
Ienclosed = 0
This is possible only if the magnetic field at point P vanishes i.e.,
\(\overrightarrow{\mathrm{B}}_{\mathrm{P}}\) = 0
(b) Open space exterior to the toroid:
Let us calculate the magnetic field BQ at point Q. We construct an Amperian loop 3 of radius r3 around the point Q. The length of the loop is
L3 = 2πr3
Ampere’s circuital law for the loop 3 is
\(\oint_{\text {loop } 1} \overrightarrow{\mathrm{B}}_{\mathrm{Q}} \cdot d \vec{l}=\mu_{0} \mathrm{I}_{\text {enclosed }}\)
Since, in each turn of the toroid loop, current coming out of the plane of paper is cancelled by the current going into the plane of paper. Thus, Ienclosed = 0
This is possible only if the magnetic field at point Question vanishes i.e.,
\(\overrightarrow{\mathrm{B}}_{\mathrm{Q}}\) = 0
(c) Inside the toroid:
Let us calculate the magnetic field BS at point S by constructing an Ampenan loop 2 of radius r2 around the point S. The length of the loop is
L2 = 2πr2
Ampere’s circuital law for the ioop 2 is
\(\oint_{\text {loop } 2} \overrightarrow{\mathbf{B}}_{\mathrm{S}} \cdot \overrightarrow{d l}\) = µ0Ienclosed
Let I be the current passing through the toroid and N be the number of turns of the toroid, then
Ienclosed = NI
\(\oint_{\text {loop } 2} \overrightarrow{\mathrm{B}}_{\mathrm{S}} \cdot d \vec{l}=\oint_{\text {loop } 2} \mathrm{~B} d l \cos \theta\) = B2πr2
\(\oint_{\text {loop } 2} \overrightarrow{\mathrm{B}}_{\mathrm{S}} \cdot d \vec{l}\) = µ0 NI
BS = µ0 \(\frac{\mathrm{NI}}{2 \pi r_{2}}\)
The number of turns per unit length is n = \(\frac{\mathrm{N}}{2 \pi r_{2}}\), then the magnetic field at point S is
BS = µ0nI
![]()
Question 85.
What do you infer from Lorentz force?
Answer:
When an electric charge Question is moving with velocity \(\vec{v}\) in the magnetic field \(\vec{B}\), it experiences a force, called magnetic force \(\overrightarrow{\mathrm{F}}_{m}\). After careful experiments, Lorentz deduced the force experienced by a moving charge in the magnetic field \(\overrightarrow{\mathrm{F}}_{m}\)
\(\overrightarrow{\mathrm{F}}_{m}\) = Question (\(\vec{v}\) × \(\vec{B}\)) …………(1)
In magnitude,
\(\overrightarrow{\mathrm{F}}_{m}\) = qvB sin θ ……….(2)
The equations (1) and equation (2) imply
(i) \(\overrightarrow{\mathrm{F}}_{m}\) is directly proportional to the magnetic field \(\vec{B}\).
(ii) \(\overrightarrow{\mathrm{F}}_{m}\) is directly proportional to the velocity \(\vec{v}\).
(iii) \(\overrightarrow{\mathrm{F}}_{m}\) is directly proportional to sine of the angle between the velocity and magnetic field.
(iv) \(\overrightarrow{\mathrm{F}}_{m}\) is directly proportional to the magnitude of the charge q.
(v) The direction of \(\overrightarrow{\mathrm{F}}_{m}\) is always perpendicular to \(\vec{v}\) and \(\vec{B}\) as \(\overrightarrow{\mathrm{F}}_{m}\) in the
cross product of \(\vec{V}\) and \(\vec{B}\).
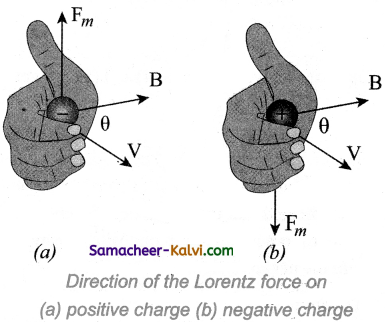
(vi) The direction of \(\overrightarrow{\mathrm{F}}_{m}\) on negative charge is opposite to the direction of \(\overrightarrow{\mathrm{F}}_{m}\) on positive charge provided other factors are identical as shown Figure.
(vii) If velocity \(\vec{v}\) of the charge Question is along magnetic field \(\vec{B}\) then, \(\overrightarrow{\mathrm{F}}_{m}\) is zero.
Question 86.
Describe the motion of a charged particle in a uniform magnetic field and derive an expression for gyro-frequency.
Answer:
Let us consider a charged particle of charge Question having mass m enters into a region of uniform magnetic field \(\vec{B}\) with velocity \(\vec{v}\) such that velocity is perpendicular to the magnetic field. As soon as the particle enters into the field, Lorentz force acts on it in a direction perpendicular to both magnetic field \(\vec{B}\) and velocity \(\vec{v}\).
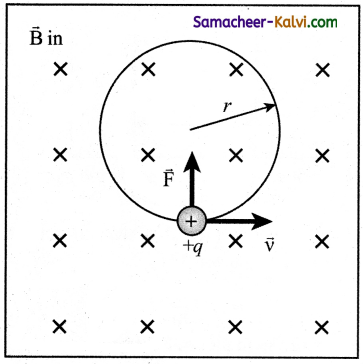
As a result, the charged particle moves in a circular orbit.
The Lorentz force on the charged particle is given by
F = q(\(\vec{v}\) × \(\vec{B}\))
Since Lorentz force alone acts on the particle, the magnitude of the net force on the particle is
\(\sum_{i} \mathrm{~F}_{i}\) = Fm = qvB
This Lorentz force acts as centripetal force for the particle to execute circular motion.
∴ qvB = m\(\frac{v^{2}}{r}\)
The radius of the circular path is
r = \(\frac{m v}{Question \mathrm{~B}}=\frac{p}{Question \mathrm{~B}}\) ……………..(1)
where p = mv is the magnitude of the linear momentum of the particle. Let T be the time taken by the particle to finish one complete circular motion, then
T = \(\frac{2 \pi r}{v}\) …………..(2)
By substituting (1) in (2), we have
T = \(\frac{2 \pi m}{Question \mathrm{~B}}\) …………….(3)
Equation (3) is called the cyclotron period. The reciprocal of time period is the frequency f which is
f = \(\frac{1}{\mathrm{~T}}\)
f = \(\frac{Question \mathrm{~B}}{2 \pi m}\) ……………(4)
In terms of angular frequency ω,
ω = 2πf = \(\frac{q}{m}\)B …………(5)
Equation (4) and equation (5) are called as cyclotron frequency or gyro-frequency.
![]()
Question 87.
Derive an expression for the force acting between two parallel current carrying conductors.
Answer:
Consider Two long straight parallel current carrying conductors separated by a distance r are kept in air. Let I1 and I2 be the electric currents passing through the conductors A and B in same direction (i.e., along z – direction) respectively. The net magnetic field at a distance r due to current I1 in conductor A is
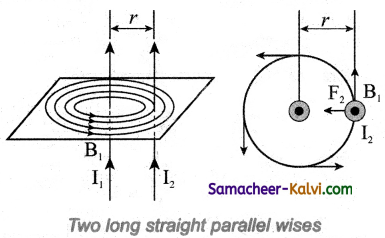
From thumb rule, the direction of magnetic field is perpendicular to the plane of the paper and inwards (arrow into the page i.e., along negative î direction.
Consider a small elemental length dl in conductor B at which the magnetic field \(\overrightarrow{\mathrm{B}}_{1}\) is present.
From equation,
\(d \overrightarrow{\mathrm{F}}=(\mathrm{I} d \vec{l} \times \overrightarrow{\mathrm{B}})\)
Lorentz force on the element dl of conductor B is
= \(-\frac{\mu_{0} \mathrm{I}_{1} \mathrm{I}_{2} d l}{2 \pi r} \hat{j}\)
Hence the force on dl of wire conductor B is directed towards the wire W1. So the length dl is attracted towards the conductor A. The force per unit length of the conductor B due to the wire conductor A is
\(\frac{\overrightarrow{\mathrm{F}}}{l}=-\frac{\mu_{0} \mathrm{I}_{1} \mathrm{I}_{2} \vec{j}}{2 \pi r}\)In the same manner, let us calculate the magnitude of net magnetic induction due to current I2 (in conductor A) at a distance r in the elemental length dl of conductor A is
\(\overrightarrow{\mathrm{B}}_{2}=\frac{\mu_{0} I_{2}}{2 \pi r} \hat{i}\)From the thumb rule, direction of magnetic field is perpendicular to the plane of the paper and outwards (arrow out to the page 0) i.e., along positive î direction.
Hence, the magnetic force at element dl of wire is W1 is
\(\vec{F}\) = \(\left(\mathrm{I}_{1} \vec{d} \times \overrightarrow{\mathrm{B}}_{2}\right)\)
= I1 dl \(\frac{\mu_{0} I_{2}}{2 \pi r}(\hat{k} \times \hat{i})\)
= \(\frac{\mu_{0} \mathrm{I}_{1} \mathrm{I}_{2} d l}{2 \pi r} \hat{j}\)
Hence the force on dl of conductor A is directed towards the conductor B. So the length dl is attracted towards the conductor B.
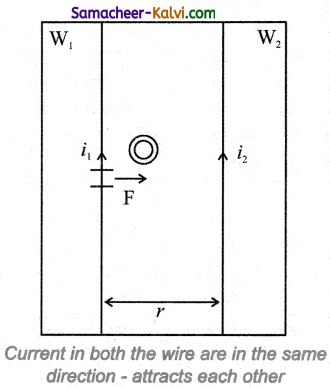
The force per unit length of the conductor A due to the conductor B is
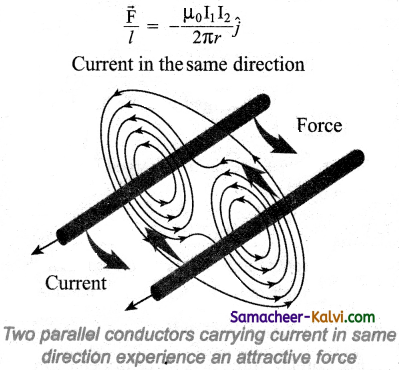
Thus the force experienced by two parallel current carrying conductors is attractive if the direction of electric current passing through them is same.
Current in the opposite direction
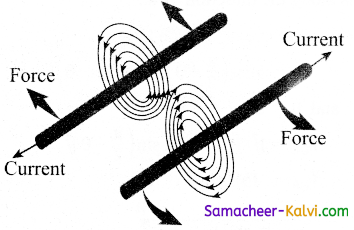
Two parallel conductors carrying current in opposite direction experience a repulsive force.
Thus the force experienced by two parallel current carrying conductors is repulsive if they carry current in the opposite directions.
![]()
Question 88.
Derive an expression for Torque acting on a current loop placed in a magnetic field.
Answer:
Let us consider a single rectangular loop PQRS kept in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\). Let a and b be the length and breadth of the rectangular loop respectively. Let n̂ be the unit vector normal to the plane of the current loop. This unit vector n̂ completely describes the orientation of the loop. Let \(\overrightarrow{\mathrm{B}}\) be directed from North pole to South pole of the magnet.
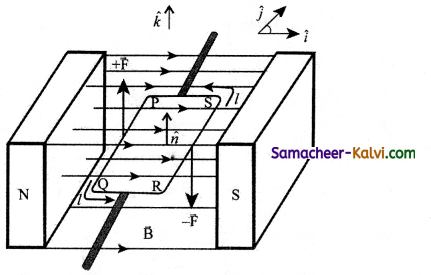 Rectangular coil placed in a magnetic field
Rectangular coil placed in a magnetic field
When an electric current is sent through the loop, the net force acting is zero but there will be net torque acting on it. For the sake of understanding, we shall consider two
configurations of the loop;
(i) unit vector h points perpendicular to the field
(ii) unit vector points at an angle θ with the field.
(i) When unit vector n is perpendicular to the field:
In the simple configuration, the unit vector n̂ is perpendicular to the field and plane of the loop is lying on xy plane. Let the loop be divided into four sections PQ, QR, RS and SP. The Lorentz force on each loop can be calculated as follows:
(a) Force on section PQ
For section PQ,
\(\vec{l}\) = a ĵ and \(\vec{B}\) = B î
= – IaB(ĵ × î) = IaB k̂
Since the unit vector normal to the plane h is along the direction of k.
(b) The force on section QR
\(\vec{l}\) = bî and \(\vec{B}\) = Bî
\(\overrightarrow{\mathrm{F}}_{\mathrm{QR}}=\mathrm{I} \vec{l} \times \overrightarrow{\mathrm{B}}=\mathrm{I} b \mathrm{~B}(\hat{i} \times \hat{i})=\overrightarrow{0}\)
(c) The force on section RS
\(\vec{l}\) = a ĵ and \(\vec{B}\) = B î
FRS = I\(\vec{l}\) × \(\vec{B}\) = IaB(ĵ × î)
= -IaB k̂
Since, the unit vector normal to the plane is along the direction of -k̂.
(d) The force on section SP
\(\vec{l}\) = -b î and \(\vec{B}\) = B î
\(\overrightarrow{\mathrm{F}}_{\mathrm{SP}}=\overrightarrow{\mathrm{I}} \times \overrightarrow{\mathrm{B}}=-\mathrm{I} b \mathrm{~B}(\hat{i} \times \hat{i})=\overrightarrow{0}\)
The net force on the rectangular loop is
\(\vec{F}_{\text {net }}=\vec{F}_{P Q}+\vec{F}_{Question R}+\vec{F}_{R S}+\vec{F}_{S P}\)
\(\overrightarrow{\mathrm{F}}_{\text {net }}\) = IaB k̂ + \(\overrightarrow{0}\) – IaB k̂ + \(\overrightarrow{0}\)
⇒ \(\overrightarrow{\mathrm{F}}_{\text {net }}\) = \(\overrightarrow{0}\)
Hence, the net force on the rectangular loop in this configuration is zero. Now let us calculate the net torque due to these forces about an axis passing through the centre
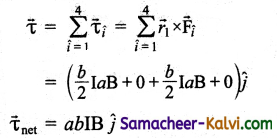
Since, A = ab is the area of the rectangular loop PQRS, therefore, the net torque for this configuration is
\(\vec{\tau}_{\text {net }}\) = ABI ĵ
When the loop starts rotating due to this torque, the magnetic field \(\vec{B}\) is no longer in the plane of the loop. So the above equation is the special case.
When the loop starts rotate about z axis due to this torque, the magnetic field \(\vec{B}\) is no longer in the plane of the loop. So the above equation is the special case.
![]()
(ii) When unit vector n̂ is at an angle θ with the field:
In the general case, the unit normal vector n̂ and magnetic field \(\vec{B}\) is with an angle θ.
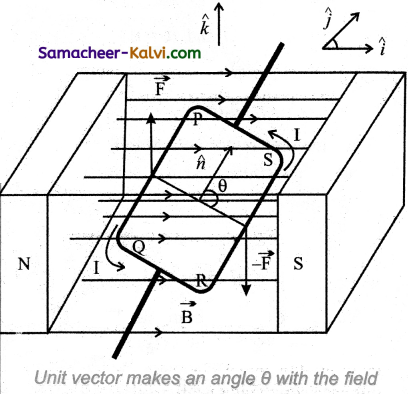
(a) The force on section PQ
\(\vec{l}\) = – aĵ and \(\vec{B}\) = Bî
= -IaB(ĵ × î) = IaB k̂
Since, the unit vector normal to the is along the direction of k.
(b) The force on section QR
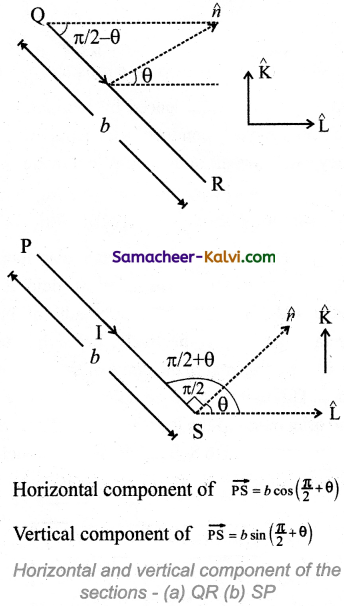
\(\vec{l}\) = b cos(\(\frac{\pi}{2}\) – θ)î – sin(\(\frac{\pi}{2}\) – θ)k̂
and \(\vec{B}\) = Bî
\(\overrightarrow{\mathrm{F}}_{\mathrm{QR}}\) = I\(\vec{l}\) × \(\vec{B}\)
= – IbB sin(\(\frac{\pi}{2}\) – θ)ĵ
\(\overrightarrow{\mathrm{F}}_{\mathrm{QR}}\) = – IbB cos θ ĵ
![]()
(c) The force on section RS
\(\vec{l}\) = aĵ and \(\vec{B}\) = Bî
\(\vec{F}\)RS = I\(\vec{l}\) × \(\vec{B}\)
= – IaB(ĵ × î) = – IaB k̂
Since, the unit vector normal to the plane is along the direction of – k̂
(d) The force on section SP
\(\vec{l}\) = b cos(\(\frac{\pi}{2}\) + θ) î + sin(\(\frac{\pi}{2}\) + θ)k̂
and \(\vec{B}\) = Bî
\(\vec{F}\)SP = I\(\vec{l}\) × \(\vec{B}\)
= IlB sin(\(\frac{\pi}{2}\) + θ)ĵ
\(\vec{F}\)SP = IbB cos θ ĵ
The net force acting on the rectangular loop is
\(\overrightarrow{\mathrm{F}}_{\text {net }}=\overrightarrow{\mathrm{F}}_{\mathrm{PQ}}+\overrightarrow{\mathrm{F}}_{\mathrm{QR}}+\overrightarrow{\mathrm{F}}_{\mathrm{RS}}+\overrightarrow{\mathrm{F}}_{\mathrm{SP}}\)\(\vec{F}\)net = Iab k̂ – IbB cos θ ĵ – IaB k̂ + IbB cos θ ĵ
\(\vec{F}\)net = \(\overrightarrow{0}\)
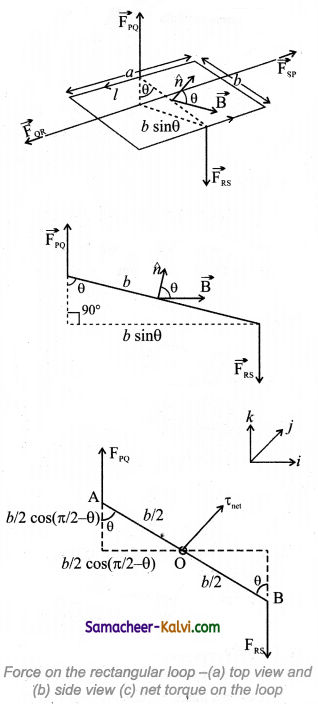
Hence, the net force on the rectangular loop in this configuration is also zero. Notice that the force on section QR and SP are not zero here. But, they have equal and opposite effects, but we assume that the loop to be rigid, so no deformation. So, no torque produced by these two sections.
Even though the forces PQuestion and RS also are equal and opposite, they are not collinear. So these two forces constitute a couple (Figure (a)). Hence the net torque produced by these two forces about the axis of the rectangular loop is given by
\(\vec{\tau}_{\text {net }}\) = baBI sin θ î = ABI sin θ k̂
From the figurre (c),
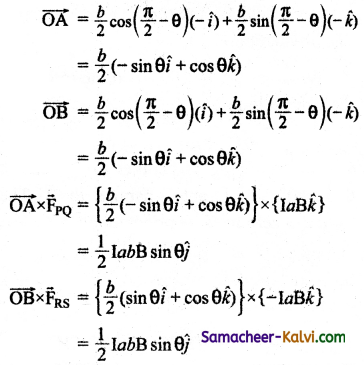
![]()
The net torque \(\vec{\tau}_{\text {net }}\) = IabB sin θ ĵ …………. (1)
It is noted that the net torque is in the positive y direction which tends to rotate the loop in clockwise direction about the y axis. If the current is passed in the other way (P → S → R → Question → P), then total torque will point in the negative y direction which tends to rotate the loop in anticlockwise direction about y axis.
Another important point is to be noted that the torque is less in this case compared to earlier Case (where the h is perpendicular to the magnetic field \(\vec{B}\). It is because the perpendicular distance is reduced between the forces FPQuestion and FRS in this case.
The equation (1) can also be rewritten in terms of magnetic dipole moment
\(\vec{p}\)m = I\(\vec{A}\) = Iab n̂
This is analogous expression for torque experienced by electric dipole in the uniform electric field,
\(\vec{\tau}_{n e t}=\vec{p} \times \overrightarrow{\mathrm{E}}\)
Special cases:
(i) When θ = 90°, then the torque on the current loop is maximum which is
\(\vec{\tau}\) = abIB ĵ
Note here \(\vec{p}\)m points perpendicular to the magnetic field \(\vec{B}\). The torque is maximum in this orientation.
(ii) When θ = 0° or 180° then the torque on the current loop is
\(\vec{\tau}\) = 0
when θ = 0°, \(\vec{p}\)m is parallel to \(\vec{B}\) and for θ = 180°, \(\vec{p}\)m is anti – parallel to \(\vec{B}\). The torque is zero in these orientations.
![]()
Question 89.
Obtain an expression for the force acting on a current carrying conductor placed in a magnetic field.
Answer:
When a current carrying conductor is placed in a magnetic field, the force experienced by the wire is equal to the sum of Lorentz forces on the individual charge carriers in the wire. Let us consider a small segment of wire of length dl, cross-sectional area A and current I. The free electrons drift Opposite to the direction of current. So the relation between current I and magnitude of drift velocity vd is
I = neAvd …………….(1)
If the wire is kept in a magnetic field \(\vec{B}\), then average force experienced by the charge (here, electron) on the wire is
\(\overrightarrow{\mathrm{F}}=-e\left(\vec{v}_{d} \times \overrightarrow{\mathrm{B}}\right)\)
Let n be the number of free electrons per unit volume, therefore
n = \(\frac{\mathrm{N}}{\mathrm{V}}\)
where N is the number of free electrons in the small element of volume V = A dl.
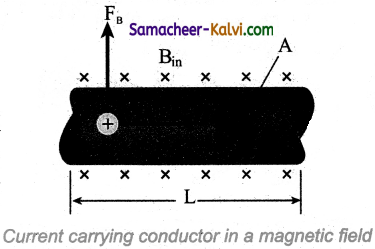
Hence Lorentz force on the wire of length dl is the product of the number of the electrons (N = nAdl) and the force acting on an electron.
\(d \overrightarrow{\mathrm{F}}=-e n \mathrm{~A} d l\left(\vec{v}_{d} \times \overrightarrow{\mathrm{B}}\right)\)The length dl is along the length of the wire and hence the current element in the wire is Id\(\vec{l}\) = -enA\(\vec{v}\)d dl. Therefore the force on the wire is
\(d \overrightarrow{\mathrm{F}}=(I d \vec{l} \times \overrightarrow{\mathrm{B}})\) …………(2)
The force in a straight current carrying conducting wire of length l placed in a uniform magnetic field is
\(\overrightarrow{\mathrm{F}}=(\overrightarrow{\mathrm{I}} \times \overrightarrow{\mathrm{B}})\) …………(3)
In magnitude,
F = BIl sin θ
(i) If the conductor is placed along the direction of the magnetic field, the angle between them is θ = 0°. Hence, the force experienced by the conductor is zero.
(ii) If the conductor is placed perpendicular to the magnetic field, the angle between them is θ = 90° Hence, the force experienced by the conductor is maximum, which is F = BIl
![]()
Question 90.
Two magnetic poles, one of which is twice stronger than the other, repel one another with a force of -2 × 10-5 N, when kept s par d at a ista of 20 cm in air. Calculate the strength of eacl pole.
Answer:
Let the pole strength of first pole = m1 = m
The pole strength of second pole = m2 = 2m
Force between them F = 2 × 10-5 N
Distance between them d= 20 × 10-2 m
Force of repulsion
F = \(\frac{\mu_{0}}{4 \pi} \frac{m_{1} m_{2}}{d^{2}}\)
= \(\frac{4 \pi \times 10^{-7}}{4 \pi} \times \frac{m \times 2 m}{\left(20 \times 10^{-2}\right)^{2}}\)
= 2 × 10-5 N
∴ 2 m2 = \(\frac{2 \times 10^{-5} \times 4 \times 10^{-2}}{10^{-7}}\)
m2 = 4
∴ m = 2 Am
∴ 2m = 2 × 2 = 4 Am
Pole strength of first pole m = 2 Am
Pole strength of second pole m = 4 Am
Question 91.
Obtain an expression for the m tic field at the centre (O) of a coil bent in the form of a rare of side 2/ carrying are as shown in the figure.
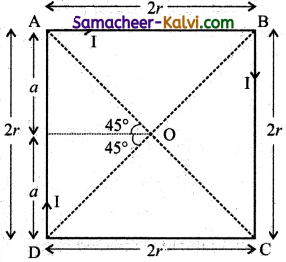
Answer:
Let Current flows through the arms be I
∴ Magnetic field through one arm of the square
B = \(\frac{\mu_{0} I}{4 \pi r}\) (sin 45° + sin 45°)

![]()
Question 92.
A bar magnet is suspended horizontally by nless ire in magnetic meridian. In order to deflect the magnet through 30° from the magnetic meridian, the upper end of th wire to be rotated by 270°. Now this magnet is replaced by another magnet. In 0rder to deflect the second magnet through the same angle from the magnetic ridi the upper end of the wire has to be rotated by 180°. What is the ratio of the magnetic moments of the two bar magnets.
Hint: (τ = Cθ)
Answer:
Let G be the deflecting torque per unit twist and M1 and M2 be the magnetic moments of the two magnets.
The deflecting torque is τ = Cθ
The restoring torque is τ = MB sin θ
In equilibrium,
deflecting torque = restoring torque
I the Magnet-I
C(270° – 30°) = M1 Bh sin θ ………..(1)
For the magnet – II
C(180° – 30°) = M2 Bh sin θ ………….(2)
Dividing by (1) and (2)
\(\frac{\mathrm{M}_{1}}{\mathrm{M}_{2}}=\frac{240^{\circ}}{150^{\circ}}\) = \(\frac{8}{5}\)
Question 93.
The force acting on each pole of magnet placed in a uniform magnetic induction of 5 × 10-4 T is 6 × 10-3 N. If the length of the magnet is 8 cm, calculate the magnetic moment of the magnet.
Answer:
Force acting on each pole F = 6 × 10-3 N
Uniform magnetic induction B = 5 × 10-4 T
Length of the magnet 2l = 8 × 10-2 m
Pole strength m = \(\frac{F}{B}=\frac{6 \times 10^{-3}}{5 \times 10^{-4}}\) = 12 Am
Magnetic moment M = m × 2l
= 12 × 8 × 10-2 = 0.96 Am2
![]()
Question 94.
Two like poles of unequal pole strength are placed 1m apart. If a pole of strength 4 Am is in equilibrium at a distance 0.2 m from one of the poles, calculate the ratio of the pole strengths of the two poles.
Answer:
Pole strength of one pole = 4 Am
Distance of separation between the poles d = 1 m
The distance of a pole strength 4 Am in equilibrium with the other pole at a distance d1 = 0.2 m
∴ The distance of other pole in equilibrium is d2 = 1 – 0.2 = 0.8 m
Force experienced at a distance d1 between the poles
F1 = \(\frac{\mu_{0}}{4 \pi} \times \frac{4 m_{1}}{(0.2)^{2}}=\frac{4 \pi \times 10^{-7} \times 4 m_{1}}{4 \pi \times(0.2)^{2}}\)
Force experienced at a distance d2 between the poles
F2 = \(\frac{\mu_{0}}{4 \pi} \times \frac{4 m_{2}}{(0.8)^{2}}=\frac{4 \pi \times 10^{-7}}{4 \pi} \times \frac{4 m_{2}}{(0.8)^{2}}\)
= \(\frac{4 m_{2}}{0.64} \times 10^{-7}\) = \(\frac{1 m_{2}}{0.16} \times 10^{-7}\)
In equilibrium, F1 = F2
m1 × 10-5 = \(\frac{m_{2}}{16}\) × 10-5
∴ \(\frac{m_{1}}{m_{2}}=\frac{1}{16}\)
∴ m1 : m2 = 1 : 16
∴ The ratio of pole strengths of the two poles = 1 : 16
![]()
Question 95.
A short bar magnet of magnetic moment 5.25 × 10-2 Am2 is placed with its axis perpendicular to the Earth’s field direction. At what distance from the centre of the magnet on
(i) its equatorial line and
(ii) its axial line, is the resultant field inclined at 45° with the Earth’s field. Magnitude of the Earth’s field at the place is 0.42 × 10-4 T.
Answer:
M = 5.25 × 10-2 Am-2; θ = 45°;
Bh= 0.42 × 10-4 T; d = ?
From the Tangent Law
\(\frac{\mathrm{B}}{\mathrm{B}_{h}}\) = tan θ
B = Bh tan θ = 0.42 × 10-4 tan45°
B = 0.42 × 10-4 T
(i) For the point on the equatorial line
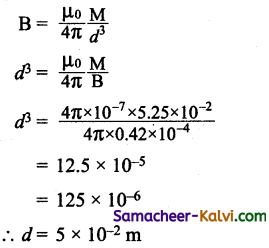
(ii) For the point on axial line
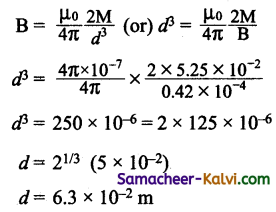
Question 96.
What will be the value of the total magnetic induction of Earth’s field at a place where dip is 60° and horizontal component is 3 × 10-5 T?
Answer:
δ = 60°; Bh = 3 × 10-5 T; B == ?
Bh = B cos δ
B = \(\frac{B_{h}}{\cos \delta}=\frac{3 \times 10^{-5}}{\cos 60^{\circ}}=\frac{3 \times 10^{-5}}{1 / 2}\)
B = 6 × 10-5 T
![]()
Question 97.
A short bar magnet is placed with its north pole pointing north. The neutral point is 10 cm away from the centre of the magnet. If B = 4 × 10-5 T, calculate the magnetic moment of the magnet.
Answer:
d = 10 × 10-2 m; B = 4 × 10-5 T; M = ?
When the north pole of a bar magnet points north, the neutral points will lie on its equatorial line.
∴ The field of the neutral point on the equatorial line of a short bar magnet is,
B = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{M}}{d^{3}}\)
∴ M = B × d3 × 107
= 4 × 10-5 (10 × 10-2)3 × 107
M = 0.4 Am2
Question 98.
A magnet of pole strength 24.6 × 10-2 Am and length 10 cm is placed at 30° with a magnetic field of 0.01 T. Find the torque acting on the magnet.
Answer:
Pole strength m = 24.6 × 10-2 Am
Length of a magnet 2l = 10 × 10-2
Angle θ = 30°
Magnetic field B = 0.01 T
Torque acting on the magnet τ = MB sin θ
Magnetic moment M = m × 2l
= 24.6 × 10-2 × 10 × 10-2 = 246 × 10-4 Nm
∴ Torque acting on the magnet = 246 × 10-4 × 0.01 sin 30°
= 246 × 10-4 × 1 × 10-2 × \(\frac{1}{2}\) = 1.23 × 10-4 Nm.
![]()
Question 99.
The magnetic moment of a bar magnet of length 10 cm is 9.8 × 10-1 A m2. Calculate the magnetic field at a point on its axis at a distance of 20 cm from its mid point.
Answer:
Length of the magnet 21 = 10 × 10-2 m
Magnetic moment M = 9.8 × 10-1 Am2
Distance of a point d = 20 × 10-2 m
The magnetic field at a distance of 20cm acting along the axial line of the bar magnet is given by,
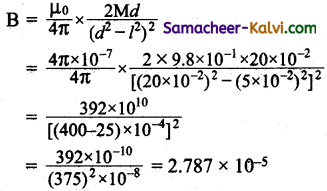
B = Resultant magnetic field = 2.787 × 10-5 Tesla
Question 100.
Two mutually perpendicular lines are drawn on a table. Two small magnets of magnetic moments 0.108 and 0.192 Am2 respectively are placed on these lines. If the distance of the point of intersection of these lines is 30 cm and 40 cm respectively from these magnets, find the resultant magnetic field at the point of intersection.
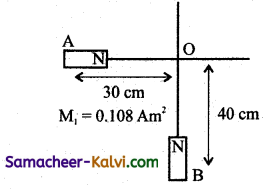
Answer:
Magnetic moment of magnet 1, M1 = 0.108 Am2
Magnetic moment of magnet 2, M2 = 0.192 Am2
Distance of magnet 1, d1 = 30 × 10-2 m
Distance of magnet 2, d2 = 40 × 10-2 m
Magnetic field at a point on the axial line due to magnet 1

![]()
Question 101.
A freely suspended magnet of moment √3 Wb-m is placed at an angle of 60° with the direction of a uniform magnetic field of strength 150 A-turns/metre. Find the moment of the couple acting on the magnet.
Answer:
Moment of the couple = 2 ml × H × sin θ = MH sin θ
M = √3 Wb-m
H = 150 A/m
θ = 60°
∴ Moment of the couple = √3 × 150 × sin 60° = 225 Wb. m
Question 102.
Calculate the current passing through a coil of radius 8 cm having 80 turns, when the field at the centre of the coil is 200 A-turn/ metre.
Answer:
Radius r = 8 × 10-2 m;
No. of turns n = 80;
Field at the centre of the coil H = 200 A/m;
Current I = ?
H = \(\frac{n \mathrm{I}}{2 r}\)
I = \(\frac{2 r}{n}\) × H
= \(\frac{2 \times 8 \times 10^{-2}}{80}\) × 200 = 0.4 A.
Question 103.
A current of 2 Amp. flows through 5 turn coil of a Tangent Galvanometer having a radius 12.5 cm, if the deflection of the needle at its centre is 45° calculate the horizontal intensity of earth’s field at that place.
Answer:
I = 2A; n = 5; r = 12.5 × 10-2 m;
θ = 45°

Question 104.
A tangent galvanometer with a coil of 50 turns and mean radius 10 cm is used at a place, when a current 0.095 Amp is passed through the galvanometer, the deflection is 45°. Calculate the horizontal component of the earth’s field.
Answer:
I = 0.095 A; n = 50; r = 10 × 10-2 m;
θ = 45°

![]()
Question 105.
A magnetic field of 104 A. turn/m produces a magnetic induction of 47π Wb / m2 in a bar of iron. Calculate the susceptibility.
Answer:
H = 104 A/m; B = 47π Wb/m2;
µ0 = – 4π × 10-7 H/m
∵ µr µ0 = \(\frac{\mathrm{B}}{\mathrm{H}}\)
µr = \(\frac{\mathrm{B}}{\mu_{0} \mathrm{H}}\)
= \(\frac{4 \pi}{4 \pi \times 10^{-7} \times 10^{4}}\)
∴ Susceptibility χm = µr – 1 = 103 – 1 = 999
Question 106.
A magnet of volume 25 × 10-6 m3 has a magnetic moment of 4π× 10-4 Am2. Calculate the intensity of the magnet.
Answer:
M = 4π × 10-4 Am2;
V = 25 × 10-6 m3
∴ Intensity of the magnetisation I = \(\frac{\mathrm{M}}{\mathrm{V}}=\frac{4 \pi \times 10^{-4}}{25 \times 10^{-6}}\) = 16 π Am.
![]()
Question 107.
The pole strength of a bar magnet is 9.872 × 10-6 Am and its length is 10cm. Calculate the magnetic intensity at a point on its axis at a distance of 20 cm from its midpoint.
Answer:
Pole strength m = 9.872 × 10-6 Am2
Length of the magnet 2l = 10× 10-2 m
Distance d = 20 cm
Magnetic moment M = 2 ml
= 2 × 9.872 × 10-6 × 5 × 10-2 Am2
Intensity of the magnetic field

Question 108.
Calculate the magnetic intensity at a point distance 20 cm from the mid point on the equatorial line of a bar magnet of pole strength of 10-5 Am and length 10 cm.
Answer:
d = 20 × 10-2 m;
l = 5 × 10-2 m;
m = 10-5 Am

Question 109.
A current of 1.5 A flows through 5 turns coil of a tangent galvanometer having a diameter 0.3 m. If the deflection of the needle at its centre is 45°, calculate the horizontal intensity of earth’s field at that place.
Answer:
By Tangent galvanometer equation,
F = \(\frac{n I}{2 r}\) = Hh tan θ
No. of turns A = 5;
Current I = 1.5 A;
Radius of the coil r = 0.15 m
Angle of deflection θ = 45°
∴ Horizontal intensity of earth’s magnetic field.
Hh = \(\frac{n \mathrm{I}}{2 r \tan \theta}\)
= \(\frac{5 \times 1.5}{2 \times 1.15 \times \tan 45^{\circ}}\)
= 25 A turn / m.
![]()
Question 110.
Calculate the moment of the couple acting on a freely suspended magnet of moment of 0.2 Wb.m. When it is placed at an angle of 30° with the direction of a uniform magnetic field of strength 50 amp. turns/m.
Answer:
Moment of the couple = 2 ml × H × sin θ = MH sin θ
Magnetic moment M = 0.2 Am2
Magnetic field strength H = 50 A/m
Angle of deflection θ = 30°
Moment of the couple = 0.2 × 50 × sin 30°
= 0.2 × 50 × \(\frac{1}{2}\) = 5 Nm
Question 111.
Find the magnetic field at the centre of a coil of radius 25 cm having 10 turns, when it .carries a current of 5 amperes.
Answer:
r = 25 × 10-2 m; n = 10; I = 5 ampere.
Magnetic field H = \(\frac{n \mathrm{I}}{2 r}\)
= \(\frac{10 \times 5}{2 \times 2.25 \times 10^{-2}}\) = 100 A turn / m.
Question 112.
Find the field at the centre of a coil of radius 16cm having 10 turns when it carries a , current of 8A.
Answer:
By Tangent galvanometer equation H = \(\frac{n \mathrm{I}}{2 r}\)
No. of turns n = 10;
Current I = 8 A;
Radius of coil ‘r’ = 16 × 10-2 m
∴ Field at the centre of the coil = \(\frac{n \mathrm{I}}{2 r}\)
= \(\frac{10 \times 8}{2 \times 16 \times 10^{-2}}\) = 250 Ampere turn / meter.
![]()
Question 113.
A beam of alpha particles and another beam of protons have same velocity enter a uniform magnetic field at right angles to the magnetic field lines. If the particles describe circular path then calculate the ratio of radii of circular path described by two beams.
Answer:
Radius of circular path r = \(\frac{m \mathrm{~V}}{\mathrm{~Bq}}\)
Radius of circular path described by alpha particles rα = \(\frac{m_{\alpha} V}{\mathrm{~B} q_{\alpha}}\)
Radius of circular path described by protons
rp = \(\frac{m_{p} \mathrm{~V}}{\mathrm{~B} q_{p}}\)
∴ \(\frac{r_{\alpha}}{r_{p}}=\frac{\frac{m_{\alpha}}{q_{\alpha}}}{\frac{m_{p}}{q_{p}}}\)
∴ \([latex]\frac{r_{\alpha}}{r_{p}}=\frac{m_{\alpha}}{q_{d}} \times \frac{q_{p}}{m_{p}}\)[/latex] ………(1)
Mass of a particle = 4 × mass of proton
∴ mα = 4 mp
Charge of a particle = 2 × charge of protons
∴ qα = 4 qp
Substituting (2) and (3) in (1)
\(\frac{r_{\alpha}}{r_{p}}=\frac{4 m_{p}}{2 q_{p}} \times \frac{q_{p}}{m_{p}}=\frac{2}{1}\)
∴ rα : rp = 2 : 1
Ratio of radii of circular path described by a particles and proton is rα : rp = 2 : 1
Question 114.
A long straight wire carrying current produces a magnetic induction of 4 × 10-6 T at a point, 15 cm from the wire. Calculate the current through the wire.
Answer:
B = 4 × 10-6 T;
a = 15 × 10-2 m; I = ?
B = \(\frac{\mu_{0} I}{2 \pi a}\)
∴ I = \(\frac{\mathrm{B} \times 2 \pi a}{\mu_{0}}\)
= \(\frac{4 \times 10^{-6} \times 2 \pi \times 15 \times 10^{-2}}{4 \pi \times 10^{-7}}\)
∴ I = 3A
Question 115.
A circular coil of 200 turns and of radius 20 cm carries a current of 5 A. Calculate the magnetic induction at a point along its axis, at a distance three times the radius of the coil from its centre.
Answer:
n = 200; a = 2 0cm = 2 × 10-1; I = 5A
x = 3a; B = ?

![]()
Question 116.
Find the magnetic induction at a point, 10 cm from a long straight wire carrying a current of 10 A.
Answer:
Distance of the point a – 10 × 10-2m
Current I = 10 A
Magnetic induction B = \(\frac{\mu_{0} I}{2 \pi a}\)
Magnetic induction B = \(\frac{4 \pi \times 10^{-7} \times 10}{2 \pi \times 10 \times 10^{-2}}\)
= 2 × 10-5 T
Magnetic induction B = 2 × 10-5 T
Question 117.
A circular coil of radius 20 cm has 100 turns wire and it carries a current of 5 A. Find the magnetic induction at a point along its axis at a distance of 20 cm from the centre of the coil.
Answer:
Number of turns n = 100
Current I = 5 A
Distance of the coil a = 20 × 10-2 m
Magnetic induction B = \(\frac{\mu_{0} n I a^{2}}{2\left(a^{2}+x^{2}\right)^{\frac{3}{2}}}\)
Magnetic induction B

![]()
Question 118.
A straight wire of length one metre and of resistance 2 Ω is connected across a battery of emf 12 V. The wire is placed normal to a magnetic field of induction 5 × 10-3 T. Find the force on the wire.
Answer:
Length of a wire l = 1 m;
Resistance of the wire R = 2 Ω
Electromotive force E = 12 V;
Magnetic induction B = 5 × 10-3 T
Force on the wire F = BIl
Current I = \(\frac{\mathrm{E}}{\mathrm{R}}=\frac{12}{2}\) = 6 A
Force on the wire F = 5 × 10-3 × 6 × 1 = 30 × 10~3 N
Force on the wire = 3 × 10-2 N
Question 119.
A circular coil of 50 turns and radius 25 cm carries a current of 6A. It is suspended in a . uniform magnetic field of induction 10-3 T. The normal to the plane of the coil makes an angle 60° with the field. Calculate the torque of the coil.
Answer:
Number of turns of a coil n = 50
Radius of the coil = 25 × 10-2 m
Current I = 6A
Magnetic field of induction in which the coil is suspended
B = 103 T
Angle θ = 60°
Torque τ = nBI.A sin θ
Area = πr2
= 3.14 × (25 × 10-2)2
= 3.14 × 625 × 10-4
= 1962.5 × 10 m2.
∴ Torque = 50 × 10-3 × 6 × 1962.5 × 10-4 × sin 60
= 300 × 1962.5 × 10-7 × \(\frac{1.732}{2}\)
= 509857.5 × 10-7
= 5.09 × 10-2 Nm
= 5.1 × 10-2 Nm
Torque on the coil = 5.1 × 10-2 Nm.
![]()
Question 120.
A uniform magnetic field 0.5 T is applied normal to the plane of the Dees of a Cyclotron. Calculate the period of the
alternating potential to be applied to the Dees to accelerate deuterons
(mass of deuterons = 3.3 × 10-27 kg and Its charge = 1.6 × 10-19 C).
Answer:
Magnetic field B = 0.5 T;
Mass of deuteron m = 3.3 × 10-27 kg
Charge of deuteron Question = 1.6 × 10-19 C
Time period = \(\frac{2 \pi m}{\mathrm{~B} q}\)
Time of period T = \(\frac{2 \times 3.14 \times 3.3 \times 10^{-27}}{0.5 \times 1.6 \times 10^{-19}}\)
= \(\frac{6.6 \times 3.14 \times 10^{-27}}{80 \times 10^{-21}}\)
= 0.25905 × 10-6 s = 2.59 × 10-7 s = 2.6 × 10-7 s
Question 121.
A solenoid is 2m long and 3 cm in diameter. It has 5 layers of windings of 1000 turns each and carries a current of 5A. Find the magnetic induction at its centre along its axis.
Answer:
l = 2m, N = 5 × 1000 turns, I = 5 A, B = ?
B = µ0 nI = µ0 \(\frac{\mathrm{N}}{l}\)
B = \(\frac{4 \pi \times 10^{-7} \times 5000 \times 5}{2}\)
B = 1.57 × 10-2 T
Question 122.
A current of 4 A flows through 5 turn coil of a tangent galvanometer having a diameter of 30 cm. If the horizontal, component of Earth’s magnetic induction is 4 × 10-5 T, find the deflection produced in the coil.
Answer:
n = 5; I = 4 A; d = 3 × 10-1 m; Bh = 4 × 10-5 T;
a = 1.5 × 10-1 m; θ = ?
I = \(\frac{2 a \mathrm{~B}_{h}}{\mu_{0} n}\) tan θ
∴ tan θ = \(\frac{\mu_{0} n I}{2 a B_{h}}\)
= \(\frac{4 \pi \times 10^{-7} \times 5 \times 4}{2 \times 1.5 \times 10^{-1} \times 4 \times 10^{-5}}\)
tan θ = 2.093
∴ θ = 64°28′
![]()
Question 123.
In a tangent galvanometer, a current of 1A produces as deflection of 30°. Find the current required to produce a deflection of 60°.
Answer:
I1 = 1 A; θ1 = 30°; θ2 = 60°; I2 = ?
I1 = k tan θ1
I2 = k tan θ2
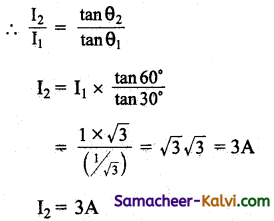
Question 124.
A long solenoid of length 3m has 4000 turns. Find the current through the solenoid if the magnetic field produced at the centre of the solenoid along its axis is 8 × 10-3 T.
Answer:
Length of solenoid l = 3m
Number of turns of solenoid N = 4000
Magnetic field at its centre B = 8 × 10-3 T
B = µ0 nI

Question 125.
A Song wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. Calculate the magnetic field at the centre of the coil having n turns.
Answer:
Let the length of the wire be l.
When it is bent into a circular loop of radius R, the magnetic field at the centre of the loop is given by

The magnetic field at the centre of the coil having n turns = n2 × magnetic field at the centre of the coil.
![]()
Question 126.
A square loop ABCD carrying current (I) is placed near and coplanarwith a long straight conductor XY carrying current (I). Calculate the net force on the loop.
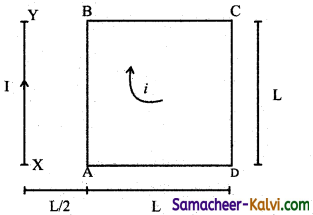
Answer:
Force acting on the side AB, due to current (I) flowing through the conductor XY is given by
F1 = \(\frac{\mu_{0}}{4 \pi} \times \frac{2 I_{i}}{\frac{L}{2}} \times L\)
= \(\frac{\mu_{0} I_{i}}{\pi}\)
Acting towards XY in the plane of the loop.
Force acting on the side CD due to current I in the conductor XY is given by
F2 = \(\frac{\mu_{0}}{4 \pi} \times \frac{2 \mathrm{I}_{i}}{\left(\frac{3 \mathrm{~L}}{2}\right)} \times \mathrm{L}\)
= \(\frac{\mu_{0} I_{i}}{3 \pi}\)
Acting away from XY in the plane of the loop. .
∴ Net force acting on the loop
F = F1 – F2
= \(\frac{\mu_{0} I_{i}}{\pi}-\frac{\mu_{0} I_{i}}{3 \pi}=\frac{\mu_{0} I_{i}}{\pi}\left[\frac{1}{1}-\frac{1}{3}\right]\)
F = \(\frac{2}{3} \frac{\mu_{0} \mathrm{I}_{i}}{\pi}\)
∴ Net force on the loop F = \(\frac{2}{3} \frac{\mu_{0} \mathrm{I}_{i}}{\pi}\)
Question 127.
A long straight wire of radius (a) carries a steady current (I). The current is uniformly distributed over its cross section. Calculate the ratio of The magnetic fields B and B’ at radial distances \(\frac{a}{2}\) and 2a respectively from the axis of the wire.
Answer:
It is given that the current is uniformly distributed over the cross section of the wire. Hence, the magnetic field at a point, inside the wire at a distance r = \(\frac{a}{2}\) from the axis of the wire is given by

B’ = \(\frac{\mu_{0} \mathrm{I}}{4 \pi a}\) ……………(2)
∴ From equation (1) and (2) we get
B = B’
Ratio of magnetic fields is B : B’ = 1 : 1
![]()
Question 128.
An electron is moving in a circular path under the influence of a transverse magnetic field of 3.57 × 10-2 T.
Answer:
If the value of \(\frac{e}{m}\) is 1.76 × 1011 C kg-1 then calculate the frequency of revolution of the electron.
Magnetic field B = 3.57 × 10-2 T
Since the electron revolves in a circular path of radius r with velocity v, at the point of equilibrium.
Centripetal force = Lorentz’s force
\(\frac{m v^{2}}{r}\) = B qv = Bev
∴ \(\frac{v}{r}=\frac{\mathrm{B} e}{m}\) ………….(1)
Frequency of revolution of the electron is
v = \(\frac{1}{T}=\frac{v}{2 \pi r}\) ……………(2)
Using equation (1) equation (2) can be Written as
∴ v = \(\frac{1}{2 \pi} \frac{\mathrm{B} e}{m}\)
v = \(\frac{1}{2 \times 3.14}\) × 3.57 × 10-2 × 1.76 × 1011
= \(\frac{6.28}{6.28}\) × 109 Hz = 1 × 109 Hz
∴ Frequency of revolution of an electron v = 1 × 109 Hz = 1 GHz
Question 129.
If a wire of length 1 metres carrying a current ‘l’. ‘A’ is bent in the form of a circle then calculate the magnitude of the magnetic moment.
Answer:
Circumference of the circle = Length of the wire
∴ 2πr = l
r = \(\frac{l}{2 \pi}\)
∴ r2 = \(\frac{l^{2}}{4 \pi^{2}}\)
Let r be the radius of the circle.
Magnetic moment M = AI
∴ M = AI = πr2l …………(2)
Substituting equation (1) in (2) We get
M = \(\pi\left(\frac{l^{2}}{4 \pi^{2}}\right) I=\frac{l^{2} \mathrm{I}}{4 \pi}\).
![]()
Question 130.
An electron of charge e moves in a circular orbit of radius r around a nucleus. The magnetic field due to orbital motion of the electron at the site of the nucleus is B. Calculate the angular velocity of the electron.
Answer:
Let the charge of the electron be e
Let the velocity of the electron be v
Let the time period of the electron be T
Let the magnetic field due to orbital motion of the electron be B
We know that when an electron moving in a circular orbit is equivalent to a current carrying loop.

![]()
Choose the correct answer:
Question 1.
If the magnetic field induction at the centre of a circular coil of radius V carrying current I is B, then the magnetic induction on the axis of the coil at a distance of √8 r is:
(a) \(\frac{\mathrm{B}}{4}\)
(b) \(\frac{\mathrm{B}}{8}\)
(c) \(\frac{\mathrm{B}}{9}\)
(d) \(\frac{\mathrm{B}}{27}\)
Answer:
(d) \(\frac{\mathrm{B}}{27}\)
Hint:

Question 2.
A magnetic field exerts a force:
(a) If the charged particle is moving along the magnetic field lines.
(b) If the charged particle is moving inclined to the magnetic field lines.
(c) On a charged particle.
(d) On a uncharged particle.
Answer:
(b) If the charged particle is moving inclined to the magnetic field lines.
Question 3.
A current carrying aluminium wire of diameter 2 mm produces a maximum magnetic field of magnitude of 2 × 10-3 T. Then the current flowing through the wire is:
(a) 5 A
(b) 20 A
(c) 10 A
(d) 40 A
Answer:
(c) 10 A
Hint:
B = \(\frac{\mu_{0} \mathrm{I}}{2 \pi \mathrm{R}}\)
2 × 10-3 = \(\frac{4 \times 3.14 \times 10^{-7} \times I}{2 \times 3.14 \times 1 \times 10^{-3}}\)
2 × 10-3 = I × 2 × 10-7+3 = I × 2 × 10-4
∴ I = \(\frac{2 \times 10^{-3} \times 10^{4}}{2}\) = 1 × 101 = 10 A
![]()
Question 4.
Choose the odd than out:
(a) magnetic field
(b) magnetic dipole moment
(c) electric dipole moment
(d) permeability
Answer:
(c) electric dipole moment
Question 5.
The value of µ0 is :
(a) 4π × 107 A/m
(b) 4π × 10-7 H/m
(c) 4π × 10-8 A/m
(d) 4π × 108 H/m
Answer:
(b) 4π × 10-7 H/m
Question 6.
Two magnetic poles kept Separated by a distance d in vacuum experience a force of 10 N. The force they would experience when kept inside a medium of relative permeability 2, separated by the Same distance is:
(a) 20 N
(b) 10N
(c) 5 N
(d) 40 N
Answer:
(a) 20 N
![]()
Question 7.
A long magnetic needle of length 2l, magnetic moment M and pole strength m is broken into two at the middle. The magnetic moment and pole strength of each piece will be:
(a) M,M
(b) \(\frac{\mathrm{M}}{2}\), \(\frac{m}{2}\)
(c) M, \(\frac{m}{2}\)
(d) \(\frac{\mathrm{M}}{2}\), M
Answer:
(d) \(\frac{\mathrm{M}}{2}\), M
Question 8.
Magnetic moment is equal to:
(a) 2lm
(b) lm
(c) \(\frac{2 l}{m}\)
(d) 2ml2
Answer:
(a) 2lm
Question 9.
Unit of magnetic flux is:
(a) Weber
(b) Weber/m2
(c) Tesla
(d) Weber/m
Answer:
(a) Weber
![]()
Question 10.
The magnetic moment of a magnet is 5 Am2. If the pole strength is 25 A m, what is the length of the magnet?
(a) 10 cm
(b) 20 cm
(c) 25 cm
(d) 1.25 cm
Answer:
(b) 20 cm
Question 11.
The magnetic needle of a tangent galvanometer is kept small because the magnetic field is:
(a) very large
(b) considered to be small and uniform at centre only
(c) such that it is convenient to handle small needle
(d) considered to be large
Answer:
(b) considered to be small and uniform at centre only
Question 12.
The ratio of magnetic inductions at a point along the axial line to that at a point on the equatorial line is:
(a) 2 : 1
(b) 1 : 2
(c) 1 : 3
(d) 3 : 1
Answer:
(b) 1 : 2
![]()
Question 13.
Magnetic induction at a point along the axial line due to a short bar is B =
(a) \(\frac{\mu_{0} \mathbf{M}}{4 \pi d^{3}}\)
(b) \(\frac{\mu_{0} 2 \mathrm{M}}{4 \pi d^{3}}\)
(c) \(\frac{\mu_{0} \mathrm{M}}{4 \pi d^{2}}\)
(d) \(\frac{\mu_{0} 2 M}{4 \pi d^{2}}\)
Answer:
(b) \(\frac{\mu_{0} 2 \mathrm{M}}{4 \pi d^{3}}\)
Question 14.
Magnetic induction at a point along the equatoriailine of a bar magnet is B =
(a) \(\frac{\mu_{0} 2 \mathrm{M}}{4 \pi d^{3}}\)
(b) \(\frac{\mu_{0} \mathrm{M}}{4 \pi d^{2}}\)
(c) \(\frac{\mu_{0} \mathbf{M}}{4 \pi d^{3}}\)
(d) \(\frac{\mu_{0} \mathrm{M}}{d^{3}}\)
Answer:
(b) \(\frac{\mu_{0} \mathrm{M}}{4 \pi d^{2}}\)
Question 15.
Select the odd man out:
(a) Permeability
(b) Susceptibility
(c) Intensity of magnetisation
(d) Permittively
Answer:
(d) Permittively
![]()
Question 16.
A bar magnet of pole strength and magnetic moment M is divided into two equal pieces by cutting it perpendicular to its length. Then,
(a) pole strength is halved and magnetic moment is halved.
(b) pole strength is doubled and magnetic moment is halved.
(c) pole strength remains same and magnetic moment is halved.
(d) pole strength is doubled and magnetic moment is doubled.
Answer:
(c) pole strength remains same and magnetic moment is halved.
Question 17.
The angle of dip is 90° at the:
(a) geographic pole
(b) magnetic pole
(c) magnetic equator
(d) 90° latitude
Answer:
(b) magnetic pole
Question 18.
The vertical component of the earth’s is magnetic field is zero at the:
(a) 45° latitude
(b) magnetic poles
(c) magnetic equator
(d) magnetic axis
Answer:
(c) magnetic equator
![]()
Question 19.
The horizontal component of Earth’s magnetic’ field is √3 times the vertical component. Then the angle of dip at that place is:
(a) 45°
(b) 60°
(c) 90°
(d) 30°
Answer:
(d) 30°
Hint:
BH = B cos θ; Bv = B sin θ
\(\frac{\mathbf{B}_{\mathbf{V}}}{\mathbf{B}_{\mathbf{H}}}\) = tan θ = \(\frac{1}{\sqrt{3}}\)
∴ θ = 30°
Question 20.
Which of the following statement is correct for the following situation.
The direction of the force experienced by a charged particle moving with a velocity v in a uniform magnetic field is
(a) parallel to both v and B
(b) perpendicular to both v and B
(c) perpendicular to B and parallel to v
(d) perpendicular to v and parallel to B
Answer:
(b) perpendicular to both v and B
Question 21.
Which of the following statements are incorrect for the following situation. The magnetic field inside a straight solenoid.
(i) is uniform throughout the solenoid
(ii) depends on current in the solenoid
(iii) depends on number of turns of the solenoid
(iv) is perpendicular to the axis of the solenoid
(a) (i) and (iv)
(b) (iii) and (iv)
(c) (ii) and (iv)
(d) (i) and (iii)
Answer:
(d) (i) and (iii)
![]()
Question 22.
Select the incorrect statement from the following statement for the given situation. The force experienced by a charged particle moving in a magnetic field B with a velocity v is zero if:
(a) v is parallel to B
(b) v is anti parallel to B
(c) v is perpendicular to B
(d) v = 0
Answer:
(c) v is perpendicular to B
Question 23.
Select the correct statements for the magnetic field due to a toroidal solenoid depends upon the,
(i) current in the solenoid
(ii) number of toms in solenoid
(iii) permeability of the core of the solenoid
(iv) radius of the toroid
(a) (i), (ii), (iv)
(b) (ii), (iii), (iv)
(c) (i), (ii), (iii)
(d) (i), (iii), (iv)
Answer:
(b) (ii), (iii), (iv)
Hint:
B = µnI
Question 24.
Choose the incorrect statement from the following case:
The direction of force experienced by a charged particle moving with a velocity in a magnetic field B is
(i) parallel to v and perpendicular to B
(ii) parallel to B and perpendicular to v
(iii) perpendicular to both v and B
(iv) parallel to both v and B
(a) (i), (ii), (iii)
(b) (ii), (iii), (iv)
(c) (i), (ii), (iv)
(d) (i), (iii), (iv)
Answer:
(a) (i), (ii), (iii)
![]()
Question 25.
Assertion:
If a charged particle enters in the region of non-uniform magnetic field in the direction of magnetic field it will I be accelerated at non-uniform state in the region.
Reason:
The force experienced by a particle of charge Question moving with a velocity \(\vec{v}\) in a magnetic field B is given by \(\overrightarrow{\mathbf{F}}=q(\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}})\)
(a) Both Assertion and Reason are true and reason explains assertion correctly
(b) Both Assertion and Reason are true and reason does not explain assertion correctly
(c) Assertion is true and Reason is false.
(d) Assertion is false and Reason is true.
Answer:
(d) Assertion is false and Reason is true.
Hint:
If v is parallel to B then force F = 0. Hence it is not accelerated in the region.
Question 26.
The inherent nature of all matter out of the following is:
(a) paramagnetism
(b) ferromagnetism
(c) diamagnetism
(d) None of the above
Answer:
(c) diamagnetism
Question 27.
The relative permeability can be expressed as:
(a) µr = 1 + µ0
(b) µr = 1 + k
(c) µr = 1 + \(\frac{\boldsymbol{k}}{\mu_{0}}\)
(d) µr = µr + k
Answer:
(b) µr = 1 + k
![]()
Question 28.
Magnetic susceptibility k is given by the relation:
(a) k = \(\frac{1}{\mathrm{H}}\)
(b) k = \(\frac{b}{\mathrm{H}}\)
(c) k = \(\frac{\mathrm{H}}{\mathrm{I}}\)
(d) k = \(\frac{\mathrm{H}}{\mathrm{B}}\)
Answer:
(a) k = \(\frac{1}{\mathrm{H}}\)
Question 29.
The ratio of flux density to the magnetic field strength inside the same medium is called:
(a) magnetic permeability
(b) intensity of magnetisation
(c) magnetic susceptibility
(d) None of these
Answer:
(a) magnetic permeability
Question 30.
Intensity of magnetisation of material is equal to:
(a) I / H
(b) M / V
(c) I + K
(d) V / M
Answer:
(b) M / V
![]()
Question 31.
The permeabilities of para and ferromagnetic materials are:
(a) greater than unity
(b) lesser than unity
(c) equal to unity
(d) negative
Answer:
(a) greater than unity
Question 32.
For which of the following substances, the magnetic susceptibility is independent of temperature?
(a) diamagnetic
(b) paramagnetic
(c) ferromagnetic
(d) diamagnetic and paramagnetic
Answer:
(a) diamagnetic
Question 33.
At curie point, a ferromagnetic material becomes:
(a) non-magnetic
(b) diamagnetic
(c) paramagnetic
(d) strongly ferromagnetic
Answer:
(c) paramagnetic
Question 34.
Electromagnets are made of soft iron because soft iron has:
(a) low susceptibility and low retentivity
(b) high susceptibility and low retentivity
(c) high susceptibility and high retentivity
(d) low permeability and high retentivity
Answer:
(b) high susceptibility and low retentivity
![]()
Question 35.
The mathematical expression for magnetic flux is:
(a) Φ = \(\frac{\overrightarrow{\mathrm{B}}}{\overrightarrow{\mathrm{A}}}\)
(b) Φ = \(\overrightarrow{\mathrm{B}}-\overrightarrow{\mathrm{A}}\)
(c) Φ = \(\overrightarrow{\text { B }} \cdot \vec{A}\)
(d) Φ = \(\frac{\overrightarrow{\mathrm{A}}}{\overrightarrow{\mathrm{B}}}\)
Answer:
(c) Φ = \(\overrightarrow{\text { B }} \cdot \vec{A}\)
Question 36.
The unit of intensity of magnetisation is:
(a) Am-2
(b) A2m
(c) Am
(d) A/m
Answer:
(d) A/m
Question 37.
Domains are due to:
(a) covalent bonds
(b) doping
(c) spin exchange interaction
(d) hysteresis loss
Answer:
(c) spin exchange interaction
![]()
Question 38.
Example of paramagnetic substance is:
(a) Bi
(b) Zn
(c) CuSO4
(d) Co
Answer:
(c) CuSO4
Question 39.
Nickel is a __________ material.
(a) diamagnetic
(b) ferromagnetic
(c) paramagnetic
(d) None of the above
Answer:
(b) ferromagnetic
Question 40.
The relation between the magnetic permeability (µ), magnetic susceptibility (K), intensity of magnetisation (I) and magnetic induction (B) is:
(a) µ = \(\frac{\mathrm{BI}}{\mathrm{K}}\)
(b) K = \(\frac{\mu \mathrm{B}}{\mathrm{I}}\)
(c) I = \(\frac{\mu \mathrm{B}}{\mathrm{K}}\)
(d) B = \(\frac{\mu \mathrm{I}}{\mathrm{K}}\)
Answer:
(d) B = \(\frac{\mu \mathrm{I}}{\mathrm{K}}\)
![]()
Question 41.
For diamagnetism, the value of relative permeability is:
(a) µr < 1
(b) µr = 1
(c) µr << 1
(d) µr >> 1
Answer:
(a) µr < 1
Question 42.
The relative permeability of a specimen is 10001 and magnetising field strength is 2500 Am-1. The intensity of magnetisation is:
(a) 0.5 × 10-7 Am-1
(b) 2.5 ×10-7 Am-1
(c) 2.5 × 10+7 Am-1
(d) 2.5 × 10-1 Am-1
Answer:
(c) 2.5 × 10+7 Am-1
Question 43.
Match the following quantities given in Column I and Column II.
| Column I | Column II |
| (i) Magnetising field (H) | (A)Vm-1 |
| (ii) Permeability | (B) Am-1 |
| (Hi) Electric field | (C) N m2 C2 |
| (iv) Permitivity | (D) N C-1 |
| (E) H m-1 |
(a) (i) – (D); (ii) – (C); (iii) – (B); (iv) – (A)
(b) (i) – (E); (ii) – (D); (iii) – (B); (iv) – (C)
(c) (i) – (A); (ii) – (C); (iii) – (B); (iv) – (D)
(d) (i) – (A); (ii) – (E); (iii) – (D); (iv) – (C)
Answer:
(d) (i) – (A); (ii) – (E); (iii) – (D); (iv) – (C)
Question 44.
Which of the following does not depend upon temperature?
(a) ferromagnetism
(b) paramagnetism
(c) diamagnetism
(d) None of these
Answer:
(c) diamagnetism
![]()
Question 45.
Unit of magnetic moment is:
(a) Weber.metre-1
(b) Weber.metre
(c) Weber.metre2
(d) ampere/metre
Answer:
(b) Weber.metre
Question 46.
If the pole strength of a magnet is 12 Am and its length is 8cm then magnetic moment of the magnet is:
(a) 9.6 Am2
(b) 96 × 10-2 Am2
(c) 0.96 × 10-2Am2
(d) 1.98 × 10-2 Am2
Answer:
(b) 96 × 10-2 Am2
Question 47.
The value of total magnetic induction of Earth’s field at a place where dip is 45° and horizontal component is 3 × 10 s T is:
(a) \(\frac{3}{\sqrt{2}}\) × 10-5 T
(b) 6 × 10-5 T
(c) 3√2 × 10-5 T
(d) √3 × 10-5 T
Answer:
(c) 3√2 × 10-5 T
![]()
Question 48.
Two short bar magnets produce null deflection in a magnetometer needle, when their centres are respectively. 30 cm and 40 cm from the needle. The ratio of their magnetic moment is:
(a) 9 : 16
(b) 27 : 64
(c) 1 : 3
(d) 3 : 4
Answer:
(b) 27 : 64
Question 49.
A magnet of volume 25 × 10-6 m3 has a magnetic moment of 4π × 10-4 Am2. The intensity of the magnet is:
(a) 4π Am-1
(b) 8π Am-1
(c) 16π Am-1
(d) 0.4π Am-1
Answer:
(c) 16π Am-1
Question 50.
If relative permeability of a bar of iron is 10,000 then its susceptibility is:
(a) 999
(b) 9999
(c) 10001
(d) 4999
Answer:
(b) 9999
![]()
Question 51.
The current passing through a coil of radius 8 cm giving 80 turns when the magnetic field at the centre of the coil is 200 A-turn/metre is:
(a) 4 A
(b) 8 A
(c) 0.8 A
(d) 0.4 A
Answer:
(d) 0.4 A
Question 52.
A sample of iron is placed to a magnetic field 100 amp turps pet metre. If the flux density of the sample is 1.2 Tesla; then which one of the following statement is correct?
(a) µ = 1.3 × 10-3 H /m µr = 930, K = 936
(b) µ = 1.2 × 10-3 H/m, µr = 955, K = 954
(c) µ = 1.1 × 10-3 H/ m, µr= 956, K = 955
(d) µ = 1.2 × 10-3 H/ m, µr = 935, K = 934
Answer:
(b) µ = 1.2 × 10-3 H/m, µr = 955, K = 954
Hint:
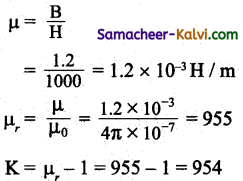
Question 53.
The magnetic susceptibility is negative for:
(a) ferromagnetic materials only
(b) paramagnetic materials only
(c) diamagnetic materials only
(d) diamagnetic materials and ferromagnetic materials
Answer:
(c) diamagnetic materials only
![]()
Question 54.
The dimension of magnetic susceptibility is
(a) ML-1T-1
(b) M°L-2T°
(c) M°L°T°
(d) M°L°T-1
Answer:
(c) M°L°T°
Question 55.
Which one of the following material is used for making permanent magnet?
(a) bronze
(b) copper
(c) platinum
(d) Alnico
Answer:
(d) Alnico
Question 56.
Which of the following is an artificial magnet?
(a) Magnetic needle
(b) Magnetic compass
(c) Horse shoe magnet
(d) All the above
Answer:
(d) All the above
Question 57.
A current I flows along the length of an ^ infinitely long straight thin walled pipe. Then the magnetic field:
(a) is different at different points inside the pipe.
(b) at all points inside the pipe is zero.
(c) at any point inside the pipe is zero.
(d) is zero only” on the axis of the pipe.
Answer:
(c) at any point inside the pipe is zero.
![]()
Question 58.
The force experienced by the charged particle in the magnetic field is:
(a) in the Y – Z plane
(b) in the X – Y plane
(c) along the negative Y – direction
(d) along the positive Y – direction
Answer:
(d) along the positive Y – direction
Question 59.
Assertion:
If a charged particle is released from rest enters in a region where uniform electric and magnetic fields act parallel to each other, then it will move along a linear path.
Reason:
The magnetic field exerts a force on the charged particle. The electric field exerts no force on it. Which one of the following statements is correct?
(a) Both assertion and reason are true and reason explains assertion correctly.
(b) Both assertion and reason are true but reason does not explain assertion correctly.
(c) Assertion is false and reason is true.
(d) Assertion is true and reason is false
Answer:
(d) Assertion is true and reason is false
Hint:
Electric force \(\overrightarrow{\mathrm{F}}_{E}\) = Question \(\vec{E}\)
Magnetic force \(\overrightarrow{\mathrm{F}}_{B}\) = v × \(\vec{B}\)
Since \(\vec{E}\) is parallel to \(\vec{B}\)
\(\vec{v}\) is parallel to \(\vec{B}\)
\(\vec{v}\) × \(\vec{B}\) = 0
Motion of the particle is not affected by \(\vec{B}\)
Question 60.
Assertion:
The charge of two particles is equal. They have masses m1 and m2. They are accelerated by the s2tme potential difference (V). So they enter a region of magnetic field and describe circular paths of radii r1 and r2. respectively. Then
\(\frac{m_{1}}{m_{2}}=\frac{r_{1}}{r_{2}}\)
Reason:
Work done to accelerate the charged particle through a potential difference V is equal to the gain in kinetic energy.
Which one of the following statement is correct?
(a) Both Assertion and Reason are true but reason does not explain assertion correctly.
(b) Both Assertion and Reason are true and reason explains assertion correctly.
(c) Assertion is false and Reason is true.
(d) Assertion is True but Reason is false.
Answer:
(c) Assertion is false and Reason is true.
Hint:
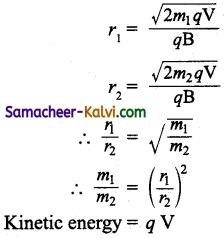
![]()
Question 61.
__________ effect of electric current is the important physical consequence of electric current.
(a) Chemical
(b) Lighting
(c) Magnetic
(d) Thermoelectric
Answer:
(c) Magnetic
Question 62.
What is produced by a steady electric current in surrounding space?
(a) Gravitational field
(b) Magnetic field
(c) Electric field
(d) Equipotential field
Answer:
(b) Magnetic field
Question 63.
Which of the following effects is a cause and a consequence of electric current?
(a) Magnetic effect
(b) Chemical effect
(c) Thermoelectric effect
(d) Mechanical effect
Answer:
(c) Thermoelectric effect
![]()
Question 64.
Match Column I with Column II.
| Column I | Column II |
| (i) A uniformly charged stationary ring | (A) Electric field |
| (ii) A uniformly charged ring rotating with a constant angular velocity | (B) Magnetic field |
| (iii) A coil carrying a current I = I0 sin ωt | (C) Magnetic moment |
| (iv) A wire carrying a constant current. | (D) Induced electric field |
| (E) Magnetising field | |
| (F) Radial magnetic field |
(a) (i) – (C); (ii) – (D); (iii) – (C) and (E); (iv) – (A), (E), (F)
(b) (i) – (E); (ii) – (F); (iii) – (B) and (E); (iv) – (B), (C), (D)
(c) (i) – (B); (ii) – (A), (B) and (C); (iii) – (A) (B) and (D); (iv) – (B)
(d) (i) – (A); (ii) – (E), (B), (C); (iii) – (E) and (F); (iv) – (A), (B), (F)
Answer:
(c) (i) – (B); (ii) – (A), (B) and (C); (iii) – (A) (B) and (D); (iv) – (B)
Question 65.
Which of the following equations represents Biot-savart law?
(a) d\(\vec{B}\) = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d l}{r^{2}}\)
(b) d\(\vec{B}\) = \(\frac{\mu_{0}}{4 \mu} \frac{\mathrm{I} d l \sin \theta}{r^{2}}\)
(c) d\(\vec{B}\) = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d \vec{l} \times \vec{r}}{r^{2}}\)
(d) d\(\vec{B}\) = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d l \times \vec{r}}{r^{3}}\)
Answer:
(d) d\(\vec{B}\) = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{I} d l \times \vec{r}}{r^{3}}\)
Question 66.
Magnetic induction (due to an infinitely long straight conductor placed in a medium of permeability p is:
(a) \(\frac{\mu_{0} \mathrm{I}}{4 \pi a}\)
(b) \(\frac{\mu_{0} \mathrm{I}}{2 \pi a}\)
(c) \(\frac{\mu \mathrm{I}}{4 \pi a}\)
(d) \(\frac{\mu \mathrm{I}}{2 \pi a}\)
Answer:
(d) \(\frac{\mu \mathrm{I}}{2 \pi a}\)
![]()
Question 67.
Of the following devices, which has small resistance?
(a) moving coil galvanometer
(b) ammeter of range 0 – 1 A
(c) ammeter of range 0 – 10 A
(d) Voltmeter
Answer:
(c) ammeter of range 0 – 10 A
Question 68.
A galvanometer of resistance G Ω is shunted with SΩ. The effective resistance of the combination is R. Then, which of the following statement is true?
(a) G is less than S
(b) S is less than Ra but greater than G.
(c) Ra is less than both G and S
(d) S is less than both G and Ra
Answer:
(c) Ra is less than both G and S
Question 69.
Nichrome wire is used as the heating element because it has:
(a) low specific resistance
(b) low melting point
(c) high specific resistance
(d) high conductivity
Answer:
(c) high specific resistance
Question 70.
Peltier coefficient at a junction of a thermocouple depends on:
(a) the current in the thermocouple
(b) the time for which current flows
(c) the temperature of the junction
(d) the charge that passes through the thermocouple
Answer:
(c) the temperature of the junction
![]()
Question 71.
In a thermocouple, the temperature of the cold junction is 20°C, the neutral temperature is 270°C. The temperature of inversion is:
(a) 520°C
(b) 540°C
(c) 500°C
(d) 510°C
Answer:
(a) 520°C
Question 72.
Joule’s law of heating is:
(a) H = \(\frac{\mathrm{I}^{2}}{\mathrm{R}}\) t
(b) H = V2 Rt
(c) H = VIt
(d) H = IR2t
Answer:
(c) H = VIt
Question 73.
In a thermocouple peltier coefficient is:
(a) more at hot junction
(b) more at cold junction
(c) same at hot and cold junction
(d) None of the above
Answer:
(c) same at hot and cold junction
![]()
Question 74.
Seebeck effect is a ____________ effect.
(a) reversible
(b) irreversible
(c) heating
(d) chemical
Answer:
(a) reversible
Question 75.
The position of the metal in Seebeck series depends upon:
(a) current
(b) electromotive force
(c) temperature
(d) potential
Answer:
(c) temperature
Question 76.
Electric arc and electric welding work on the principle of effect of current.
(a) chemical
(b) heating
(c) lighting
(d) mechanical
Answer:
(b) heating
Question 77.
Joule’s law is verified using:
(a) Magnetometer
(b Calorimeter
(c) Galvanometer
(d) Joule’s calorimeter
Answer:
(d) Joule’s calorimeter
![]()
Question 78.
Joule heating effect is undesirable in:
(a) galvanometer
(b) calorimeter
(c) transformer
(d) transformer and dynamo
Answer:
(d) transformer and dynamo
Question 79.
Which of the following is not thermoelectric effect?
(a) Seebeck effect
(b) Peltier effect
(c) Joule effect
(d) Thomson effect
Answer:
(c) Joule effect
Question 80.
The appliances that work on the principle of heating effect of current are:
(a) electric iron, torch light
(b) electric iron, electric bell
(c) electric iron, electric heater
(d) electric iron, electric heater and electric toaster
Answer:
(d) electric iron, electric heater and electric toaster
![]()
Question 81.
In an electric circuit, fuse wire is:
(a) not at all connected
(b) connected in series
(c) connected
(d) connected in parallel
Answer:
(b) connected in series
Question 82.
The constituents of the element by which the fuse wire is made up of are:
(a) Lead 37% zinc63%
(b) Lead 37% tin 63%
(c) Lead 28% tin 72%
(d) Zinc 28% tin 72%
Answer:
(b) Lead 37% tin 63%
Question 83.
According to Joule’s law of heating, the heat produced is given by :
(a) IR2t
(b) I2Rt
(c) IRt2
(d) I2R2t
Answer:
(b) I2Rt
Question 84.
Heater coils are all made up of an alloy called:
(a) manganin
(b) constantan
(c) nichrome
(d) alloy
Answer:
(c) nichrome
![]()
Question 85.
Cyclotron was devised by:
(a) Oersted
(b) Faraday
(c) Lawrence
(d) Lorentz
Answer:
(c) Lawrence
Question 86.
The magnetic Lorentz force on a charged particle in a uniform magnetic field, when it is at rest is:
(a) Zero
(b) BqV
(c) BqV cos θ
(d) BqV tan θ
Answer:
(a) Zero
Question 87.
The unit of Thomson coefficient is:
(a) volt
(b) ampere
(c) volt per°C
(d) ohm
Answer:
(c) volt per°C
Question 88.
The plane of T.G coil should be in a direction of:
(a) East-West
(b) Eastern North
(c) North-South
(d) Western North
Answer:
(c) North-South
![]()
Question 89.
The Torque experienced by a rectangular current loop placed perpendicular to a uniform magnetic field is:
(a) maximum
(b) zero
(c) finite minimum
(d) infinity
Answer:
(b) zero
Question 90.
The direction of magnetic field:
(a) depends on the direction of the current in the conductors.
(b) does not depend on the direction of the current in the conductors.
(c) does not depend on the direction of the motion of the conductor.
(d) depends on the direction of motion of the conductor.
Answer:
(a) depends on the direction of the current in the conductors.
Question 91.
The unit of magnetic induction is:
(a) weber
(b) ampere/m2
(c) tesla
(d) weber/m2 or tesla
Answer:
(d) weber/m2 or tesla
Question 92.
Which of the following works on the principle of tangent law?
(a) Deflection magnetometer
(b) Moving coil galvanometer
(c) Voltmeter
(d) Tangent galvanometer
Answer:
(d) Tangent galvanometer
![]()
Question 93.
Which of the following gives the direction of magnetic field?
(a) Faraday’s law
(b) Ohm’s law
(c) Maxwell’s rule
(d) Biot-Savart law
Answer:
(c) Maxwell’s rule
Question 94.
In a tangent galvanometer the angle between the planes of the circular coil and the circular scale is:
(a) 0°
(b) 25°
(c) 90°
(d) 180°
Ans
(c) 90°
Question 95.
The magnetic needle of a tangent galvanometer is kept small because the magnetic field is:
(a) very large
(b) considered to be small and uniform at centre only
(c) such that it is convenient to handle small needle
(d) very small
Answer:
(b) considered to be small and uniform at centre only
Question 96.
Tangent galvanometer is used for measuring:
(a) potential
(b) current
(c) resistance
(d) electric power
Answer:
(b) current
![]()
Question 97.
The tangent galvanometer is most sensitive around a deflection of:
(a) 0°
(b) 45°
(c) 30°
(d) 60°
Answer:
(b) 45°
Question 98.
In a tangent galvanometer a current 1 A, produces a deflection of 30°. The current required to produce a deflection of 60° is:
(a) 3 A
(b) 2 A
(c) √3 A
(d) \(\frac{1}{\sqrt{3}}\)
Answer:
(a) 3 A
Question 99.
An ammeter of resistance 0.8 Ω can measure current upto 1 A. The shunt resistance connected with ammeter so that it can measure current upto 5.0 A is:
(a) 2 Ω
(b) 0.2 Ω
(c) 20 Ω
(d) 4 Ω
Answer:
(b) 0.2 Ω
Question 100.
Fuse wire is an alloy of:
(a) Lead and Tin
(b) Tin and Copper
(c) Lead and Copper
(d) Lead and iron
Answer:
(a) Lead and Tin
![]()
Question 101.
What is the reduction factor of a tangent galvanometer having 6 turn coil of diameter 30 cm, if the horizontal intensity of earth’s field at the pole is 50 A-tum/m?
(a) 2
(b) 3.5
(c) 1.5
(d) 2.5
Answer:
(d) 2.5
Question 102.
A coil of 50 turns and radius 10 cm and another coil of 25 turns and radius 5 cm are connected in series. If the current flowing through the coil is 3A, then the ratio of magnetic fields at the centre of the first coil to that at the centre of the second coil is:
(а) 1 : 2
(b) 1 : 1
(c) 2 : 1
(d) 1 : 4
Answer:
(b) 1 : 1
Question 103.
A tangent galvanometer produces deflection of 45° for a current of 0.3 A at a place, where the horizontal component of earth’s magnetic field is 30-A-turn/m. If the diameter of the coil of the tangent galvanometer is 10 cm, then the number of turns of the coil is:
(a) 20
(b) 5
(c) 10
(d) 14
Answer:
(c) 10
![]()
Question 104.
Two conductors each of length 12m be parallel to each other at a distance of 15 cm in air. The current in each conductor is 300 A. Then the force tending to pull the conductors together is:
(a) 14.4 N
(b) 2.88 N
(c) 1.44 N
(d) 0.72 N
Answer:
(c) 1.44 N
Question 105.
A galvanometer of resistance 50 Ω is shunted with a wire of 10 ohm. The current through the galvanometer when a current of 12 A flows in the circuit is:
(a) 1 A
(b) 4 A
(c) 6 A
(d) 2 A
Answer:
(b) 4 A
Question 106.
The magnetic field of induction applied to a cyclotron is 0.3 T. The frequency of the RF oscillator required to accelerate a particle of mass 1.67 × 10-27 kg is :
(a) 45.7 Hz
(b) 4.57 kHz
(c) 4.57 MHz
(d) 45.7 kHz
Answer:
(c) 4.57 MHz
![]()
Question 107.
The ratio of time periods of proton and alpha particle kept in a uniform magnetic field is:
(a) 1 : 2
(b) 2 : 1
(c) 1 : 3
(d) 1 : 4 .
Answer:
(b) 2 : 1
Question 108.
Which of the following combination of current and time will produce more heat in a heating element? ,
(a) 4 ampere current flowing for 3 minutes
(b) 2 ampere current flowing for 5 minutes
(c) 2 ampere current flowing for 10 minutes
(d) 5 ampere current flowing for 2 minutes
Answer:
(d) 5 ampere current flowing for 2 minutes
Question 109.
Magnetic flux density at the centre of a circular coil of diameter 20 cm carrying a current of 5 A kept in air is:
(a) 6.28 × 10-5 T
(b) 3.14 × 10-5 T
(c) 10-7 T
(d) 1.57 × 10-5 T
Answer:
(b) 3.14 × 10-5 T
![]()
Question 110.
The resistance of a wire is 10 ohm at 20°C. The temperature coefficient of the material of the wire is 0.004 per°C. The resistance of the wire at 40°C is:
(a) \(\frac{11.6}{1.08}\) ohm
(b) \(\frac{11.8}{1.04}\) ohm
(c) \(\frac{1.16}{1.08}\) ohm
(d) \(\frac{10.6}{1.08}\) ohm
Answer:
(a) \(\frac{11.6}{1.08}\) ohm
Question 111.
The ratio of the resistance of a conductor at a temperature of 15°C to its resistance at a temperature of 37.5°C is 4 : 5. What is the temperature coefficient of resistance of the conductor?
(a) \(\frac{1}{150}\)
(b) \(\frac{1}{25}\)
(c) \(\frac{1}{50}\)
(d) \(\frac{1}{75}\)
Answer:
(b) \(\frac{1}{25}\)
Question 112.
A current of 2A flows through a resistor for 8 second and a current of 8 A flows through the same resistor for 2 second. The ratio of the heats developed will be:
(a) 1 : 4
(b) 1 : 2
(c) 1 : 1
(d) 1 : 3
Answer:
(a) 1 : 4
![]()
Question 113.
The expression for Bohr magneton is:
(a) \(\frac{e h}{4 \pi m}\)
(b) \(\frac{4 \pi m}{e h}\)
(c) \(\frac{4 e h}{\pi m}\)
(d) \(\frac{2 \pi m}{e h}\)
Answer:
(a) \(\frac{e h}{4 \pi m}\)
Question 114.
The numerical value of Bohr magneton is:
(a) 9.27 × 1024 Am2
(b) 92.7 × 10-27 Am2
(c) 9.67 × 1024 Am2
(d) 9.27 × 10-24 Am2
Answer:
(d) 9.27 × 10-24 Am2
Question 115.
The magnetic polarity of the current carrying solenoid is given by:
(a) Maxwell’s rule
(b) End rule
(c) Ampere’s rule
(d) Biot-Savart law
Answer:
(b) End rule
![]()
Question 116.
\(\oint \overrightarrow{\mathrm{B}} \cdot d \vec{l}=\mu_{0} \mathrm{I}_{0}\) is the mathematical representa-tion of:
(a) Biot-Savart law
(b) Ampere’s swimming rule
(c) Ohm’s law
(d) Ampere’s circuital law
Answer:
(d) Ampere’s circuital law
Question 117.
A long closely wound helical coil is called:
(a) circular loop
(b) coil
(c) solenoid
(d) toroid
Answer:
(c) solenoid
Question 118.
The magnetic field associated with each single turn are almost:
(a) curves
(b) straight lines
(c) parabola
(d) concentric circles
Answer:
(d) concentric circles
![]()
Question 119.
The value of magnetic field at a point outside of a solenoid is:
(a) finite
(b) infinity
(c) zero
(d) nearly zero
Answer:
(d) nearly zero
Question 120.
At the interior mid point of a solenoid, the magnetic field is:
(a) weak
(b) strong
(c) weak and along the axis of a solenoid
(d) strong and along the axis of a solenoid
Answer:
(d) strong and along the axis of a solenoid
Question 121.
The magnetic induction at a distance R from a long linear conductor is:
(a) directly proportional to current and distance R
(b) directly proportional to current but inversely proportional to the distance R
(c) directly proportional to the square of the current but inversely to the distance R
(d) directly proportional to the current but inversely to the square of the distance (R2)
Answer:
(d) directly proportional to the current but inversely to the square of the distance (R2)
![]()
Question 122.
Magnetic induction (B) at a point due to a straight conductor carrying current is:
(a) B = \(\frac{\mu \mathrm{I}}{4 \pi d}\)
(b) B = \(\frac{4 \pi \mu \mathrm{I}}{d}\)
(c) B = \(\frac{\mathrm{I}}{4 \pi d}\)
(d) B = \(\frac{\mu \mathrm{I}}{2 \pi d}\)
Answer:
(d) B = \(\frac{\mu \mathrm{I}}{2 \pi d}\)
Question 123.
A conductor of length 3 m is at right angles to a uniform magnetic field of 0.6 T. A current of 2 A flowing through the conductor produces a force of:
(a) 1.6 N
(b) 1.8 N
(c) 3.6 N
(d) 3.2 N
Answer:
(c) 3.6 N
Question 124.
The number of turns of a coil of radius 10 cm required to produce a magnetic field of 4π × 10-4 T at the centre with a current of 4 A is:
(a) 500
(b) 100
(c) 25
(d) 50
Answer:
(d) 50
![]()
Question 125.
The magnitude and direction of Lorentz force is:
(a) \(\overrightarrow{\mathrm{F}}=q(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{V}})\)
(b) \(\overrightarrow{\mathrm{F}}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
(c) \(\overrightarrow{\mathrm{F}}=\vec{v}(Question \times \overrightarrow{\mathrm{B}})\)
(d) F = \(\overrightarrow{\mathrm{B}}(Question \times \vec{v})\)
Answer:
(b) \(\overrightarrow{\mathrm{F}}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
Question 126.
The expression for time period of motion of a charged particle in a uniform magnetic field is given by:
(a) T = \(\frac{\mathrm{B} q}{2 \pi m}\)
(b) T = \(\frac{2 \pi m}{\mathrm{~B} q}\)
(c) T = \(\frac{B q}{2 m}\)
(d) T = \(\frac{2 m}{\pi B q}\)
Answer:
(b) T = \(\frac{2 \pi m}{\mathrm{~B} q}\)
Question 127.
The magnetic induction (B) at the centre of a current carrying circular loop is:
(a) \(\frac{\mu \mathrm{I}}{2 r}\)
(b) \(\frac{\mu . r}{2 \mathrm{I}}\)
(c) \(\frac{\mu \mathrm{I} r}{2}\)
(d) \(\frac{2 \mu}{\mathrm{I} r}\)
Answer:
(a) \(\frac{\mu \mathrm{I}}{2 r}\)
![]()
Question 128.
The relation between current and drift velocity is:
(a) I = nAvd
(b) I = nAvde
(c) I = \(\frac{n \mathrm{~A}}{e v_{d}}\)
(d) I = \(\frac{e v_{d}}{n \mathrm{~A}}\)
Answer:
(b) I = nAvde
Question 129.
The magnetic field at the centre of a circular coil of radius r carrying current I is:
(a) \(\frac{\mathrm{I}}{2 r}\)
(b) \(\frac{\mu_{0} I}{2 r}\)
(c) \(\frac{\mu_{0} I r}{2}\)
(d) \(\frac{\mathrm{I}}{2 \mu_{0} r}\)
Answer:
(a) \(\frac{\mathrm{I}}{2 r}\)
Question 130.
Which one of the following is particle accelerator?
(a) Nuclear reactor
(b) Cyclotron
(c) Geiger counter
(d) Lightning arrester
Answer:
(b) Cyclotron
![]()
Question 131.
A cyclotron is a device for accelerating:
(a) light particles
(b) heavy particles
(c) charged particles
(d) electrons
Answer:
(c) charged particles
Question 132.
Cyclotron can accelerate particle.
(a) beta
(b) an elementary
(c) alpha
(d) any
Answer:
(c) alpha
Question 133.
Cyclotron cannot accelerate:
(a) electrons
(b) a particles
(c) proton
(d) deuteron
Answer:
(a) electrons
Question 134.
Two parallel wires carrying same current in the same direction will experience:
(a) attractive force
(b) magnetic force
(c) electric force
(d) repulsive force
Answer:
(a) attractive force
![]()
Question 135.
A galvanometer can be converted into voltmeter by connecting a:
(a) low resistance in parallel
(b) low resistance in series
(c) high resistance in parallel
(d) high resistance in series
Answer:
(d) high resistance in series
Question 136.
The voltage sensitivity of a galvanometer is given by:
(a) \(\frac{n \mathrm{BA}}{\mathrm{CG}}\)
(b) \(\frac{\mathrm{CG} \theta}{n \mathrm{BA}}\)
(c) \(\frac{n \mathrm{AG}}{\mathrm{A}} \theta\)
(d) \(\frac{n \mathrm{~A} \theta}{\mathrm{CBG}}\)
Answer:
(a) \(\frac{n \mathrm{BA}}{\mathrm{CG}}\)
Question 137.
If A is the loop area and I is the strength of current flowing through it, then magnetic moment is:
(a) \(\frac{I}{A}\)
(b) IA
(c) \(\frac{\mathrm{A}}{\mathrm{I}}\)
(d) \(\frac{\mathrm{I}}{\mathrm{IA}}\)
Answer:
(b) IA
Question 138.
Peltier effect is the converse of:
(a) Joule effect
(b) Raman effect
(c) Thomson effect
(d) Seebeck effect
Answer:
(d) Seebeck effect
![]()
Question 139.
The unit of reduction factor of tangent galvanometer is:
(a) no unit
(b) tesla
(c) ampere
(d) ampere / degree
Answer:
(c) ampere
Question 140.
In a tangent galvanometer, for a constant current, the deflection is 30°. The plane of the coil is rotated through 90°. Now, for the same current, the deflection will be:
(a) 30°
(b) 60°
(c) 90°
(d) 0°
Answer:
(d) 0°
Question 141.
Which of the following principles is used in a thermopile?
(a) Thomson effect
(b) Peltier effect
(c) Seebeck effect
(d) Joule’s effect
Answer:
(c) Seebeck effect
![]()
Question 142.
An ideal voltmeter has:
(a) zero resistance
(b) finite resistance between zero and G;
(c) resistance greater than G but less than infinity
(d) infinite resistance
Answer:
(d) infinite resistance
Question 143.
Which of the following graphs represent the variation of magnetic susceptibility with absolute temperature for a ferromagnetic material?
(a) 
(b) 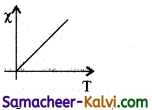
(c) 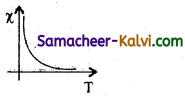
(d) 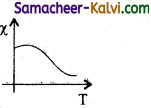
Answer:
(d) 
Hint:
As temperature of a ferromagnetic material is increased its susceptibility first remains constant. Then decreases that is shown by the graph (d).
![]()
Question 144.
Which one of the following is not made up of soft iron?
(a) Core of transformer
(b) Core of dynamo
(c) Electromagnet
(d) Magnet of a loudspeaker
Answer:
(d) Magnet of a loudspeaker
Hint:
Magnet of a loudspeaker is made from permanent magnet.
Question 145.
Which one of the following graphs represent the relationship between magnetic moment and temperature of magnet?
(a) 
(b) 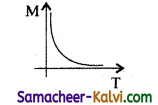
(c) 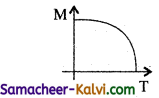
(d) 
Answer:
(c) 
Hint:
When temperature is increased, the magnetic moment will increase and at critical temperature it becomes zero.
Question 146.
A bar magnet is hung by a thin cotton thread in a uniform, horizontal magnetic field and is in equilibrium.
The energy required to rotate it by 60° is W. Now the torque required to keep the magnet in this new position is:
(a) \(\frac{\mathrm{W}}{\sqrt{3}}\)
(b) √3 W
(c) \(\frac{\sqrt{3} \mathrm{~W}}{2}\)
(d) \(\frac{2 \mathrm{~W}}{\sqrt{3}}\)
Answer:
(b) √3 W
Hint:
Workdone in rotating the magnet
W = MB(cos θ0 – cos θ) = MB(cos 0° – cos 60°)
W = MB[1 – \(\frac{1}{2}\)] = \(\frac{\mathrm{MB}}{2}\)
∴ MB = 2 W ……….(1)
Torque on a magnet in this position is τ = M × B = M B sin θ = 2 W sin 60°
τ =2W × \(\frac{\sqrt{3}}{2}\) = √3 W
![]()
Question 147.
When a current flows along length of a long thin cylindrical shell on which charge is uniformly distributed. Match the physical quantities given in Column I and II.
| Column I | Column II |
| (i) Magnetiafield at all points lying inside the shell. | (A) inversely proportional to the distance from the axis of the coil. |
| (ii) Magnetic field at any point outside the shell | (B) infinity |
| (iii) Magnetic field is maximum of the shell. | (C) inversely proportional to radius of the ‘ shell. |
| (iv) Magnetic field on the axis of the shell. | (D) just outside the shell |
| (E) zero |
(a) (i) – (E); (ii) – (A); (iii) – (D); (iv) – (C)
(b) (i) – (A); (ii) – (B); (iii) – (E); (iv) – (D)
(c) (i) – (B); (ii) – (E); (iii) – (C); (iv) – (B)
(d) (i) – (C); (ii) – (D); (iii) – (E); (iv) – (A)
Answer:
(a) (i) – (E); (ii) – (A); (iii) – (D); (iv) – (C)