TN State Board 11th Chemistry Important Questions Chapter 1 Basic Concepts of Chemistry and Chemical Calculations
Question 1.
Give a brief account of classification of matter.
Answer:
(i) Matter can be classified as solids, liquids, and gases based on their physical state.
(ii) Matter can also be classified into mixtures and pure substances based on chemical composition.
Question 2.
Distinguish between a homogeneous and heterogeneous mixture.
Answer:
| Homogeneous | Heterogeneous |
| A homogeneous mixture is one in which the components are uniformly mixed. Every portion of the mixture has the same compositon and proportion, (isotropic) | A heterogeneous mixture is not uniform. The properties of the mixture is not uniform throughout, (anisotropic) |
![]()
Question 3.
Define the following:
(i) Element,
(ii) Compound.
Answer:
(i) An element consists of only one type of atom. An atom is the smallest electrically neutral particle, being made up of fundamental particles, namely electrons, protons, and neutrons.
(ii) Compounds are made up of molecules which contain two or more atoms of different elements. Properties of compounds are different from those of their constituent elements. The constituents of a compound is present in a fixed ratio by weight.
Question 4.
Give two examples of elementary molecules which are
(i) Monoatomic
(ii) Diatomic and
(iii) Polyatomic.
Answer:
(i) Monoatomic molecules: Copper (Cu) and Gold(Au)
(ii) Diatomic molecules: Hydrogen (H2) and Oxygen (O2)
(iii) Polyatomic molecules: Phosphorous (P4) and Sulphur (S8)
![]()
Question 5.
Mention the characteristics of a compound.
Answer:
(i) The compound is made up of two or more atoms of different elements in a definite ratio by weight.
(ii) The properties of a compound is different from those of their constituent elements.
Question 6.
Why atomic masses are called as relative atomic masses?
Answer:
The mass of an atom (10-27 kg) is too small to be measured directly. They are measured with reference to a standard atom. Hence they are called relative atomic masses.
Question 7.
Which atom is considered to be a standard atom by IUPAC to measure atomic masses and what is its atomic mass?
Answer:
The C-12 atom is considered as standard by the IUPAC (International Union of Pure and Applied Chemistry), and it’s mass is fixed as 12 amu (or) u.
![]()
Question 8.
Define a.m.u or unified atomic mass.
Answer:
The quantity \(\frac{1}{12}\) mass of an atom of carbon -12 is known as the atomic mass unit, (a.m.u). The actual mass of one atom of carbon-12 is 1.9914 × 10-23 g or 1.9914 × 10-26 kg.
Thus,
1 a.m.u = \(\frac{1.9924 \times 10^{-23}}{12}\)
= 1.66 × 10-24 g = 1.66 × 10-27 kg
∴ Atomic mass of an element = \(\begin{gathered}
\text { Mass of one atom } \\
\text { of the element } \\
\hline 1 \text { a.m.u }
\end{gathered}\)
Question 9.
Define relative atomic mass.
Answer:
The relative atomic mass is defined as the ratio of the average atomic mass factor to the unified atomic mass unit.
![]()
Question 10.
Calculate the mass of the following atoms in a.m.u (unified atomic mass).
Answer:
(i) Oxygen: average mass of oxygen atom = 2.656 × 10-23 g
(1 a.m.u= 1.6605 × 10-27 kg (or) 1.6605 × 10-24 gram).
(ii) Mass of an oxygen atom = 2.656 × 10-23 g
The mass of oxygen atom in a.m.u = Average mass of oxygen atom in gram / (1.66 × 10-23)
= \(\frac{2.656 \times 10^{-23} \mathrm{~g}}{1.6605 \times 10^{-24} \mathrm{~g}}\)
= 1.599 × 10
= 15.99 a.m.u
Question 11.
The atomic mass of oxygen is 16. What is the actual mass of an oxygen atom?
Answer:
Actual mass of an oxygen atom = The atomic mass of an element in a.m.u × 1.66 × 10-24 g
= 16 × 1.66 × 10-24
= 2.656 × 10-23 g
![]()
Question 12.
The relative abundance of 6C12, 6C13 and 6C14 are 98.892%, 1.108% and 2 × 10-10 respectively. Calculate the average atomic mass of carbon.
Answer:
Average atomic mass of carbon = (12 × % abundance of C12 + 13 × % abundance of C13 +14 × % abundance of C14) / 100
given % abundances of C12 = 98.892
C13 = 1.108
C14 = 2 × 10-10
Since 2 × 10-10 is so small compound to 100, it can be neglected.
Avereage atomic mass of carbon = \(\frac{12 \times 98.892+13 \times 1.108}{100}\) = 12.01 a.m.u
Question 13.
The relative abundance of 10Ar36, 10Ar38, 10Ar40 are 0.337%, 0.063% and 99.6% respectively. Calculate the average atomic weight of Argon.
Answer:
Average atomic weight of Argon = (36 × % abundance of Ar36 + 38 × % abundance of Ar38 + 40 × % abundance of Ar40) / 100
given % abundances of Ar36 = 0.337
Ar38 = 0.063
Ar40 = 99.6
![]()
Question 14.
Define relative molecular mass.
Answer:
Relative molecular mass is defined as the ratio of the mass of a molecule to the unified atomic mass unit.
Question 15.
Calculate the molecular masses of the following:
(i) KMn04
Answer:
Molecular mass of KMnO4 = 1 × atomic mass of K +1 × atomic mass of Mn + 4 × atomic mass of O atomic mass of K = 39.098 ≈ 39
atomic mass of Mn = 54.938 ≈ 55
atomic mass of ‘O’ = 15.99 ≈ 16
∴ Molecular mass of KMn04. = 39 + 55 + 4 × 16 = 158 u.
(ii) NaOH
Molecular mass of NaOH = 1 × atomic mass of Na + 1 × atomic mass of O + 1 × atomic mass of H
= 1 × 23 + 1 × 16 + 1 × 1 = 23 + 16 + 1 = 40u.
(iii) H2C2O4.2H2O (crystalline oxalic acid)
Molecular mass of H3C2O4.2H2O = 2 × atomic mass of H + 2 × atomic mass of C + 4 × atomic mass of O + 2 × molecular mass of H2O
= 2 × 1 + 2 × 12 + 4 × 16 + 36
= 2 + 24 + 64 + 36
= 126u.
(iv) C6H12O6 (glucose)
Molecular mass of C6H12O6 = 6 × atomic mass of C + 12 × atomic mass of H + 6 × atomic mass of O
= 6 × 12 + 12 × 1 + 6 × 16
= 72 + 12+ 96 = 180u
![]()
Question 16.
Explain the term “mole”.
Answer:
(i) Mole is the SI unit to represent a specific amount of a substance.
(ii) One mole is the amount of substance of a system which contains as many elementary particles as there are in 12g of carbon-12-isotope.
(iii) Mole represents the mass in gram of 6.022 × 1023 entities (atom or molecule /ion).
(iv) 1 mole of any substance contains 6.023 × 1023 entities.
Question 17.
Give the relationship between the number of mole of the substance and its gram molecular mass.
Answer:

Question 18.
Calculate the number of atoms / molecules present in the following:
(i) 10 gram of mercury
Atomic mass of Hg = 200.59
Gram atomic mass of Hg = 200.59 g
1 mol of Hg = 200g = 6.023 × 1023 atoms
10 g = \(\frac{6.023 \times 10^{23}}{200}\) × 10
= 0.301 × 1023
= 3.01 × 1022 atoms
![]()
(ii) 1.8 gram of water
Molecular mass of H2O = 18
gram molecular mass of H2O = 18 g
1 mol of H2O = 18g of H2O
= 6.023 × 1023 molecules of H2O
1.8 g of H2O = \(\frac{6.023 \times 10^{23}}{18}\) × 1.8
= 6.023 × 1022 molecules
(iii) 100 gram of sulphur dioxide
Molecular formula of sulphur dioxide = SO2
Molecular mass of sulphur dioxide = 64
1 mole of SO2 = 64g of SO2
= 6.023 × 1023molecules
100g of SO2 = \(\frac{6.023 \times 10^{23}}{64}\) × 100
= 9.41 × 1023 molecules.
(iv) 1 kg of acetic acid (CH3COOH)
Molecular mass of acetic acid = 60
1 mol of acetic acid= 60g of acetic acid
= 6.023 × 1023 molecules
1000g of acetic acid = \(\frac{6.023 \times 10^{23}}{60}\) × 1000
= 1.0 × 1025 molecules
(v) 46 gram of sodium
Atomic mass of sodium = 23 a.m.u
1 mol of Na = 23g = 6.023 × 1023 atoms
46g = \(\frac{6.023 \times 10^{23}}{23}\) × 46
= 12.046 × 1023 atoms.
![]()
Question 19.
Calculate the number of moles present in the following:
Number of mol = (Weight of the substance in g) / (gram molecular weight (or) gram atomic weight)
(i) 50g of CaCl2
Weight of CaCl2 = 50g ,
gram moleular weight = 40 + 71 = 111
∴ number of mol = \(\frac{50}{111}\) = 0.45 mol
(ii) 120g of NaOH
Weight of NaOH = 40g
gram moleular weight = 40 g
∴ number of mol = \(\frac{40}{40}\) = 1 mol
(iii) 46g of ethanol
Weight of ethanol = 46 g
gram molecular mass of ethanol (C2H5OH) = 46
∴ number of mol = \(\frac{46}{46}\) = 1 mol
(iv) 90 g of magnesium oxide
Weight of MgO = 90 g
gram molecular weight of MgO = 24 + 16 = 40
∴ number of mol = \(\frac{90}{40}\) = 2.25 mol
(v) 19.5 g of potassium
Weight of potassium = 19.5 g
gram atomic mass of potassium = 39
∴ number of mol = \(\frac{19.5}{39}\) = 0.5 mol
![]()
Question 20.
Define Avogadro number.
Answer:
The total number of entities (atoms, molecules, ions, electrons etc…) present in one mole of any substance is equal to 6.022 × 1023. This number is called Avogadro number.
Question 21.
State Avogadro hypothesis.
Answer:
Avogadro hypothesis that equal volume of all gases under the same conditions of temperature and pressure contain equal number of molecules.
Question 22.
The relative molecular mass of sulphuric acid (H2S04) is 98 a.m.u. What is its molar mass?
Answer:
Molar mass of H2SO4 = 98g mol-1.
![]()
Question 23.
Define molar volume.
Answer:
The volume occupied by one mole of any substance in the gaseous state at a given temperature and pressure is called molar volume. The standard temperature is 273K (0°C) and the standard pressure is 1 atm.
Question 24.
Calculate the number of moles present in 9 grams of ethane.
Answer:
Molecular formula of ethane is C2H6
Motecuhr weight of ethane = 2 × 12 + 6 × 1 = 30 u
Molecular mass of ethane = 30g of mol-1
Number of mol = \(\frac{\text { Weight of substance }}{\text { Molar mass }}\)
= \(\frac{9}{30}\) = 0.3 mol
![]()
Question 25.
Calculate the number of molecules of oxygen gas that occupies a volume of 224 ml at 273K at 3 atm.
Answer:
Step – 1:
To find the volume O2 at 273K at 1 atm
\(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
P1 = 3atm: V1 =224 ml: T1 = 273K
P2 = 1 atm: V2 = ? T2 = 273K
\(\frac{3 \times 224}{273}=\frac{1 \times \mathrm{V}_{2}}{273}\)
V2 = 3 × 224 = 672ml at NTP
Step-2:
22400 ml of O2 at NTP = 1 mol of O2
= 6.023 × 1023 molecules
672 ml at NTP = \(\frac{6.023 \times 10^{23}}{22400}\) × 672
= 0.18 × 1023 molecules
= 1.8 × 1022 molecules.
![]()
Question 26.
Calculate the volume occupied at STP by the following:
(i) 88 gram of CO2
Answer:
1 mol of CO2 = 44gof CO2
= 22400 cm3 at STP
88g of CO2 = 2 × 22400 cm3 = 44800 cm3
(ii) 0.5 mole of methane
Answer:
1 mol of CH4 = 22400 cm3 at NTP
0.5 mol of CH4 = 22400 × 0.5.
= 11200 cm3 at NTP
(iii) 3.0115 × 1023 molecules of sulphur dioxide.
1 mol of SO2 = 6.023 × 1023 molecules of SO2
= 22400 cm3 at STP
3.0115 × 1023 molecules of SO2 = \(\frac{22400 \times 3.0115 \times 10^{23}}{6.023 \times 10^{23}}\)
= 11200 cm3 or 11.2 L at STP
![]()
Question 27.
Define gram equivalent mass of an element.
Answer:
Gram equivalent mass of an element, compound or ion is the mass of their species that combines or displaces 1.008g hydrogen or 8g oxygen or 35.5g chlorine.
Question 28.
What is equivalence factor ‘n’? How is it useful in determining equivalent mass of a substance?
Answer:
Equivalence factor (n) = \(\frac{\text { Molar mass }\left(\mathrm{g} \mathrm{mol}^{-1}\right)}{\text { equivalent mass }\left(\mathrm{g} \mathrm{eq}^{-1}\right)}\)
The usefulness of this factor is that the equivalent masses of all the substances can be calculated whether it is an acid, base, salt, or an oxidising or reducing agent.
![]()
Question 29.
What is the equivalence factor (n) for
(i) H2SO4
Answer:
‘n’ factor for H2SO4 = \(\frac{\text { molar mass of the acid }}{\text { equivalent mass of the acid }}\)
= \(\frac{98}{49}\) = 2
(ii) Ba(OH)2
Answer:
‘n’ factor for Ba(OH)2 = \(=\frac{\text { molar mass of } \mathrm{Ba}(\mathrm{OH})_{2}}{\text { equivalent mass of } \mathrm{Ba}(\mathrm{OH})_{2}}\)
Molar mass of Ba(OH)2 = 137 + 2 × 16 + 2 × 1
= 137 + 32 + 2 = 171
Equivalent mass of Ba(OH)2 = \(\frac{\text { molar mass }}{\text { acidity }}\)
= \(\frac{171}{2}\) = 85.5
∴ ‘n’ factor for Ba(OH)2 = \(\frac{171}{85.5}\) = 2
(iii) K2Cr2O7
Answer:
Molar mass of K2Cr2O7 = 2 × 39 + 2 × 52 + 7 × 16
= 78 + 104 + 112 = 294
In acid medium Cr2O7-2 is rediced to Cr+3
Cr2O7-2 + 6e + 14H+ → 2Cr+3 + 7H2O
Equivalent mass of K2Cr2O7 = \(\frac{\text { molar mass }}{\text { No. of electrons taken up }}\)
= \(\frac{294}{6}\) = 49
∴ ‘n’ factor = \(\frac{294}{49}\) = 6 eq. mol-1.
![]()
Question 30.
Calculate the equivalent mass of the following:
(i) Zn
(ii) CO3-2
(iii) NO3–
(iv) H3PO4
Answer:
(i) For elements:
Equivalent mass = \(\frac{\text { Atomic mass }}{\text { valency }}\)
= \(\frac{63.4}{2}\) = 31.7 g eq-1
(ii) For ions:
Equivalent mass = (sum of the atomic masses of atoms present in the ion) / charge on the ion
For CO3-2 ion
Equivalent mass = (1 × atomic mass of ‘N’ + 3 × atomic mass of ‘O’) / 2
= \(\frac{12+3 \times 16}{2}=\frac{60}{2}\) = 30 g eq-1
(iii) For NO3– ion equivalent mass:
= (1 × atomic mass of ‘N’ + 3 × atomic mass of ‘O’) / 1
= \(\frac{14+3 \times 16}{1}\) = 62 g eq-1
(iv) For acids:
Answer:

![]()
Question 31.
0.456g of a metal gives 0.606g of its chloride. Calculate its equivalent mass.
Answer:
By definition, the equivalent mass of a metal is the number of parts by weight of the element that will combine or displace 35.5 parts by weight of chlorine
Weight of metal chloride = 0.606 g
Weight of the metal formed = 0.456 g
∴ Weight of chlorine = 0.150 g
0.150 g of chlorine combines with = 0.606 g of the metal
35.5 g of chlorine combines with = \(\frac{0.606}{0.150}\) × 35.5 g = 143.42 g
∴ Equivalent mass = 143.42 g eq-1
Question 32.
1.05 g of the metal gave an oxidation 1.5 g of its oxide. Calculate the equivalent mass.
Answer:
By definition, the equivalent mass of a metal is the mass of the metal that will combine or displace 8g of oxygen (equivalent mass of oxygen = 8 g eq-1)
Weight of metal oxide = 1.5 g
Weight of the metal = 1.05 g
Weight of oxygen = 0.45g
0.45 g of oxygen combines with = 1.05 g of the metal
8.0 g of oxygen will combines with = \(\frac{1.05}{0.45}\) × 8.0 g = 18.7 g
The equivalent mass of the metal is 18.7 g eq-1.
![]()
Question 33.
Calculate the equivalent masses of the following:
(i) HCl
Answer:
Molar mass of HC1 = 1 + 35.5 = 36.5
Basicity of HCl = 1
Equivalent mass of HCl = \(\frac{36.5}{1}\) = 36.5 g eq-1.
(ii) HNO3
Answer:
Basicity of HNO3 = 1 + 14 + 3 × 16 = 63
∴ Equivalent mass of HNO3 = \(\frac{63}{1}\) = 63 g eq-1.
(iii) Oxalic acid H2C2O4
Molar mass of oxalic acid (H2C2O4) = 2 × 1 + 2 × 12 + 4 ×16 = 90 Basicity of oxalic acid = 2
∴ Equivalent mass = \(\frac{90}{2}\) = 45 g eq-1
(iv) Crystalline oxalic acid, H2C2O4 . 2H2O
Molar mass of crystalline Oxalic add (H2C2O4 . 2H2O) = Molar mass of oxalic acid + 2 × molar mass of H2O)
= 90 + 2 × 18 = 126
Basicity = 2
∴ Equivalent mass of crystalline oxalic acid = \(\frac{126}{2}\) = 63 g eq-1
(v) Ferrous sulphate
Answer:
Molar mass of ferrous sulphate = atomic mass of ‘Fe’ + atomic mass of ‘S’ + 4 × atomic mass of ‘O’
= 56 + 32 + 4 × 16 = 152
In reactions, Fe+2 ion is oxidised to Fe+3 ion
Fe+2→ Fe+3 + e
∴ ‘n’ factor = 1 (no. of electron involved in half reaction)
∴ Equivalent mass = \(\frac{\text { Molar mass }}{\text { No. of } e^{-\text {involved }}}\)
= \(\frac{152}{1}\)
= 152 g eq-1.
![]()
Question 34.
Calculate the equivalent mass of the following:
(i) Aluminium hydroxide
Answer:
Molar mass of Al(OH)3 = Atomic mass of ‘Al’ + 3 × Atomic mass of ‘O’ + 3 × Atomic mass of ‘H’
= 27 + 3 + 16 + 3 × 1 = 78
Acidity = 1
Equivalent mass of Al(OH)3 = \(\frac{\text { Molar mass }}{\text { acidity }}\)
= \(\frac{78}{3}\) = 26 g eq-1
(ii) Sodium hydroxide
Answer:
Molar mass of NaOH = 23 + 16+ 1 = 40
Acidity = 1
∴ Equivalent mass = \(\frac{\text { Molar mass }}{\text { acidity }}\)
= \(\frac{40}{1}\) = 40 g eq-1
(iii) Potassium sulphate
Answer:
Molar mass of K2SO4 = 2 × Atomic mass of ‘K’ + 1 × Atomic mass of ‘S’ + 4 × Atomic mass of ‘O’
= 2 × 40 + 1 × 32 + 4 × 16
= 80 + 32 + 64 = 176
∴ Equivalent mass odf salt = (\(\left(\frac{\text { atomic mass of cation }}{\text { valency }}\right)\) + \(\left(\begin{array}{c}
\text { sum of atomic equivalent } \\
\text { mass of anion } \\
\hline \text { valency }
\end{array}\right)\))
= \(\frac{40}{1}\) + \(\frac{32+64}{2}\)
= 40 + 48 = 88 g eq-1.
![]()
Question 35.
Define
(i) Empirical formula of a compound,
(ii) Molecular formula of a compound.
Answer:
(i) Empirical formula:
It is the simplest formula of a compound which gives the ratio of the number of different atoms present in one molecule of the compound.
(ii) Molecular formula:
Molecular formula of a compound gives the actual number of different atoms present in one molecule.
Question 36.
3.24g of titanium reacts with oxygen to form 5.40g of the metal oxide. Find the empirical formula of the compound?
Answer:
Step 1:
To find percentage composition of titanium and oxygen.
Weight of the metal oxide = 5.40 g
Weight of the metal = 3.24 g .
Weight of oxygen = 2.16 g
5.40 g of metal oxide contains = 3.24 g of metal
100 g of metal oxide will contains = \(\frac{3.24}{5.40}\) × 100 g = 60 g
∴ Percentage of titanium = 60
Percentage of oxygen = (100 – 60) = 40
![]()
Step 2:
To find the empirical formula

Question 37.
A substance an analysis, gave the following percentage composition, Na = 43.4 %, C = 11.3 %, O = 43.3 % calculate its empirical formula.
Answer:
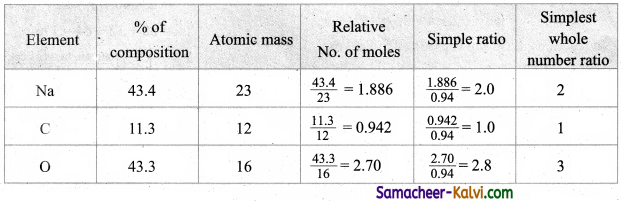
Question 38.
An organic compound contains the following composition by mass: C = 92.3 %; H = 7.7 %. At STP, 10L of the gas has the mass of 11.6g. Find the molecular formula of the compound.

Answer:
The empirical formula is CH.
The empirical formula mass = 12 + 1 = 13
To find the molecular mass:
10 L of the gas at STP weigh = 11.6 g
22.4L of the gas at STP will weigh = \(\frac{1}{12}\) × 22.4 g = 25.98 ≈ 26
n = \(\frac{\text { Molar mass }}{\text { Empirical formula mass }}=\frac{26}{13}\) = 2
Hence, the molecular formula = (Empirical formula)n
(CH)2 = C2H2
The molecular formula of the compound is C2H2.
![]()
Question 39.
An organic compound has the following composition by mass: C .= 40.92 %, H = 4.58 %, and the rest oxygen. The molar mass of the compound is 176 g mol-1. Determine the molecular formula of the compound.
Answer:
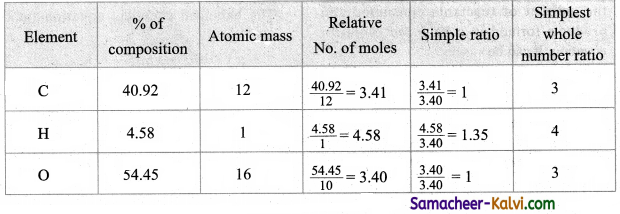
The empirical formula is C3H4O3.
Empirical formula mass = 3 × 12 + 4 × 1 + 3 × 16 = 88
Molar mass = 176 g mol-1
n = \(\frac{\text { Molar mass }}{\text { Empirical formula }}=\frac{176}{88}\) = 2
Molecular formula = (Empirical formula)n
= (C3H4O3)2
= C6H8O6
![]()
Question 40.
An inorganic compound an analysis gave the following composition. Na = 14.31 %, S = 9.97 %, H = 6.22 %, O = 69.5 %. Assume all the hydrogen atoms are present in combination with oxygen zas water of crystallization. The molar mass of the compound is 322g mol-1. Find its molecular formula.
Answer:
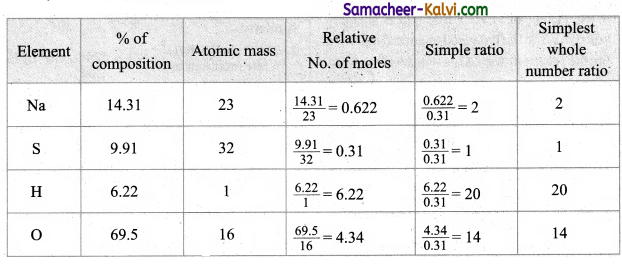
The Empirical formula is Na2SH20O14.
Since all hydrogen are present as water of hydration, the number of mole of water present in the compound is 10H2O.
Hence, the empirical formula Na2SO4.10H2O.
Empirical formula mass of the compound = 2 × 23 + 1 × 32 + 4 × 16 + 10 × 18 = 322.
Molar mass of the compound = 322 g mol-1
n = \(\frac{\text { Molar mass }}{\text { Empirical formula mass }}\)
= \(\frac{322}{322}\) = 1
Hence the molecular formula is Na2SO4 10H2O.
![]()
Question 41.
What do you understand by the term ‘stoichiometry of the reaction’?
Answer:
Stoichiometry gives the relationship between the amount of reactants consumed and products formed in a balanced chemical equation. It can be
(i) the number of moles of reactants / products
(ii) masses of the reactants / products
(iii) If the reaction is between gases, the volumes of reactants / products represented in a balanced chemical equation.
Question 42.
How many moles of barium sulphate is precipitated when one mole of aluminium sulphate completely reacts with barium chloride?
Answer:
The balanced chemical equation for the reaction is
Al2(SO4)3 + 3BaCl2 → 3BaSO4 + 2AlCl3.
As per stoichiometry, 1 mol of Al2(SO4)3 completes reacts with 3 mol of BaCl2 and produce 3 mole of barium sulphate. Hence, number of mol of BaSO4 precipitated is 3.
![]()
Question 43.
What is the amount of silver oxide formed when 11.04 g of silver carbonate is strongly heated? Write the balanced chemical equation for the reaction.
Answer:
Ag2CO3 → 2AgO + CO2.
Molar mass og Ag2CO3 = 2 × atomic mass of ‘Ag’ + atomic mass of ‘C’ + 3 × atomic mass of ‘O’
= 2 × 108 + 12 + 3 × 16
= 276 u
Molar mass of AgO = atomic mass of ‘Ag’ + atomic mass of ‘O’
= 108 + 16 = 124 g mol-1
When silver carbonate is heated, carbondioxide leaves as gas. and silver oxide remains as a residue.
According to the equation,
One mole of Ag2CO3 = 2 × atomic mass of ‘Ag’ + atomic mass of ‘C’ + 3 × atomic mass of ‘O’
= 2 × 108 + 12 + 3 × 16
= 216 + 12 + 48 = 276 u
Molar mass of AgO = atomic mass of ‘Ag’ + atomic mass of ‘O’
= 108 + 16 = 124 g mol-1
When silver carbonate is heated, carbondioxide leaves as gas. and silver oxide remains as a residue.
According to the equation,
One mole of Ag2CO3 leaves = 2 mol of AgO as residue
276 g of Ag2O = 124 g of AgO
11.04 of Ag2O = \(\frac{124}{276}\) × 11.04 g of AgO
= 4.96 g
![]()
Question 44.
How much volume of hydrogen is liberated when 0.12g of magnesium reacts with dilute hydrochloric acid?
Answer:
The balanced chemical equation for the reaction is
Mg + 2HCl → MgCl2 + H2
Atomic mass of Mg = 24g mol-1
According to the equation,
1 mol of Mg (24g) will liberate 1 mol of H2 = 22.4 L at STP
24g of Mg = 22.4 L of H2 at STP
0.12 g of Mg = \(\frac{22.4}{24}\) × o.12g of H2 at STP
= 0.112 L or = 112 cm3 at STP
Question 45.
How much volume of nitrogen and hydrogen are required to produce 100cm3 of ammonia?
Answer:
The balanced equation for the reaction is,
N2 + 3H2 → 2NH3
According to the equation,
2 × 22400 cm3 of NH3 is produced by 1 mol of N2 = 22400 cm3
Similarly,
2 × 22400 cm3 of NH3 are produced by = 3 × 22400 cm3 of H2
100 cm3 of NH3 will be produced by = \(\frac{3 \times 22400}{2 \times 22400}\) × 100 = 150 cm3
![]()
Question 46.
A temperature of about 3000°C is produced when Aluminium reduces ferric oxide and the reaction is given below.
2 Al + Fe2O3 → Al2O3 + 2 Fe
In one process 124 g of aluminium reacted with 601 g of ferric oxide.
(i) Calculate the mass of Al2O3 formed.
(ii) How much of the excess reagent is left at the end of the reaction?
Answer:
The balanced equation for the reaction is,
2Al + Fe2O3 → Al2O3 + 2Fe
(2 x 27) (160) (102)
Number of mol of aluminium taken = \(\frac{\text { mass of Al taken }}{\text { gram atomic weight }}\)
= \(\frac{124}{27}\) = 4.6 mol
No. of mol of Fe2O3 taken = \(\frac{\text { mass of } \mathrm{Fe}_{2} \mathrm{O}_{3} \text { taken }}{\text { gram molecular weight }}\)
= \(\frac{601}{160}\) = 3.75 mol
According to equation,
2 mol of al reacts with = 1 mole of Fe2O3
4.6 mole of Al will react with = \(\frac{1}{2}\) × 4.6
= 2.3 mol of Fe2O3
number of mol of Fe2O3 taken = 3.75 mol
number of mol of Fe2O3 reacted = 2.30 mol
Hence, Al is the limiting reagent and 1.45 mol of Fe2O3 will be left behind, unreacted.
2 mol of Aluminium = 54 g of Al = 102 g of Al2O3
124 g of Aluminium = \(\frac{102}{54}\) × 124
= 234 g of Al2O3
Mass of Fe2O3 left behind = No. of molecular × gram molecular unit
= 1.45 × 160 = 232 g
![]()
Question 47.
Explain the term limiting reagent.
Answer:
A limitating reagent is one which is consumed completely in a reaction. The amount of product (i.e., number of moles of product) formed one always determined by the starting moles of limitating reagent.
Question 48.
3 grams of hydrogen reacts with 29g of O2 to yield H2O.
(i) Which is the limiting reagent?
2H2 + O2 → 2H2O
2 mol 1 mol 2 mol
Number of mole of H2 taken = \(\frac{3}{2}\) = 1.5
Number of molel of O2 taken = \(\frac{29}{32}\) = 0.9.62
∴ 2 mole of H2 react with 1 mole of O2
∴ 1.5 mol of H2 will \(\frac{1}{2}\) × 1.5 = 0.75 mole of O2
react with \(\frac{1}{2}\) x 1.5
Available mole of O2 (0.9062) > required mol of O2 (0.75)
Thus, O2 is in excess and therefore, H2 will be the limiting reagent.
(ii) Calculate the maximum amount of H2O that can be formed.
2 mole of H2 give 2 mole of H2O.
(ii) Calculate the amount of one of the reactant which remains unreacted.
2 mole of H2 react with 1 mole of O2.
1.5 mole of H2 will give 1.5 mol of H2O.
(iii) Calculate the amount of one of the reactant which remains unreacted.
2 mole of H2 react with 1 mole of O2.
1.5 mole of H2 react with 0.75 mole of O2.
ExcessO2 = 0.9062 – 0.75 = 0.1562 mol.
![]()
Question 49.
Give examples of redox reactions in daily life.
Answer:
(i) When an apple is cut, it turns brown after some time. This is because of oxidation.
(ii) Resting of iron is a redox reaction.
(iii) Oxidation of carbohydrates, lipids etc., to CO2 and H2O produce energy in the living organisms.
Question 50.
Calculate the oxidation number of underlined atoms of the following:
(i) KMnO4
KMnO4 (Mn in KMnO4)
Oxidation number of K = 1
Oxidation number of Mn = x
Oxidation number of O = -2
= + 1 + x + 4(-2) = 0
x – 7 = 0
x = + 7 .
Hence the oxidation no.of Mn in KMnO4 = +7
(ii) K2Cr2O7
Answer:
K2Cr2O7 (Cr in K2Cr2O7)
Oxidation number of K = +1
Oxidation number of Cr = x
Oxidation number of O = -2
2 + 2x – 14 = 0
2x -12 = 0
x = + 6
Hence, the oxidation no. of Cr in K2Cr2O7 + 6
![]()
(iii) Na2S4O6
Answer:
Na2S4O6(S in Na2S4O6)
Oxidation number of sodium = 1
Oxidation number of sulphur = x
Oxidation number of Oxygen = -2
i.e. 2 + 4x – 12 = 0
4x – 10 = 0 x = 2.5
This is known as average oxidation state of sulphur. But by definition, oxidation number cannot be fractional. When the compound contains two or more atoms of the same element in different oxidation states chemical bonding method is used to find the oxidation number of elements.
The structure of the compound is
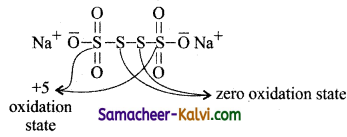
i.e., oxidation number of each sulphur atom linked with the other in the middle is zero, while the oxidation number of each of the remaining two sulphur atom is +5.
(iv) NO3–
Answer:
NO3– (N in NO3–)
Oxidation number of nitrogen = x
Oxidation number of oxygen = -2
x + 3 (- 2) = – 1
x – 6 = – 1
x = + 5
Hence, the oxidation number of nitrogen in NO3– is +5.
![]()
(v) H4P2O7
Answer:
H4P2O7 (P in H4P2O7 ‘
Oxidation number of hydrogen = + 1
Oxidation number of phosphorous = x
Oxidation number of oxygen = -2
4 + 2x- 14 = 0
2x- 12 = 0
x = + 6
Hence, the Oxidation number of phosphorous in H4P2O7 is + 6.
(vi) ClO3–
Answer:
ClO3– (Cl in ClO3–)
Oxidation number of chlorine = x
Oxidation number of oxygen = -2
x + 3 (- 2) = – 1
x – 6 = – 1 or
x = 5
The oxidation no. of chlorine in ClO3– is + 5.
![]()
(vii) ASO3-2
Answer:
ASO3-2 (AS in ASO3-2)
Oxidation number of arsenic = x
Oxidation number of oxygen = -2
x + 3 (- 2) = – 2
x – 6 = – 2 (or) x = + 3
Hence, the oxidation number of arsenic in arsenics oxide ASO3-2 is + 3.
(viii) S2O3-2
Answer:
S2O3-2 (S in S2O3-2)
Oxidation number of sulphur = x
Oxidation number of oxygen = -2
2x + 3 (- 2) => 2x – 6 = – 2 (or) 2x = 4 or x = +2
Hence, the oxidation number of sulphur is
S2O3-2 is + 2.
(ix) C6H12O6
Answer:
(C in C6H12O6)
Oxidation number of carbon = x
Oxidation number of hydrogen = +1
Oxidation number of oxygen = -2
6x + 12 – 12 = 0 (or) 6x = 0 (or) x = 0
In organic compounds containing carbon, oxygen and hydrogen, the oxidation number of carbon atom is determined by the formula.
Oxidation number of ‘C’ atom = \(\frac{n_{\mathrm{O}} \times 2-n_{\mathrm{H}}}{n_{\mathrm{C}}}\)
Where n0 = number of oxygen atoms
nH = number of hydrogen atoms
nC = number of carbon atoms
![]()
(x) Na2[Fe(CN)6]
Na2[Fe(CN)6] (Fe in Na2 [Fe(CN)6])
This compound contains a cation and a complex anion [Fe(CN)6]-4
Let the oxidation number of Iron = x
Each cyanide ion has charge = – 1
The sum of the oxidation number of the metal ion and the charges carried by negative ions should be equal to the charge as the ion. They
x – 6 = -4 or x = + 2.
Hence, Fe is in +2 oxidation state in this compound.
Question 51.
Give examples for the following redox reactions.
(i) Combination
Answer:
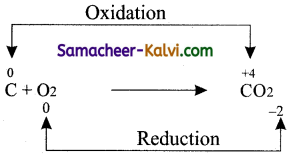
(ii) Decomposition
Answer:
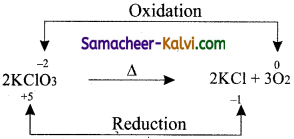
(iii) Metal displacement reactions Oxidation
Answer:
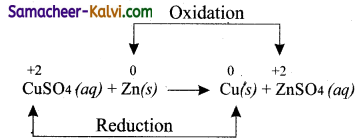
![]()
(iv) Disproportionation
Answer:
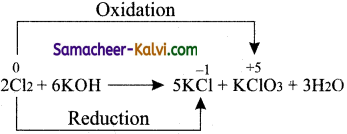
Question 52.
Explain the term competitive electron transfer reaction with an example.
Answer:
When a strip of metallic copper in sliver nitrate solution taken in a beaker and after some time, the solution slowly turns blue. This is due to the formation of Cu2+ ions, i.e., copper replaces silver from silver nitrate. The reaction is,
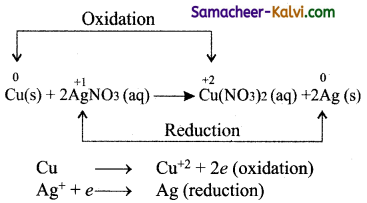
It indicates that between copper and silver, copper has the tendency to release electrons and silver to accept electrons. This type of metal displacement reactions is known as competitive electron transfer reactions.
![]()
Question 53.
Balance the following equations by oxidation number method.
(i) CuO + NH3 → Cu + N2 + H2O
Answer:
Step-1: To find atoms undergoing change in oxidation.
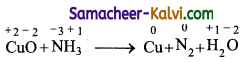
Step-2:
To find total increase and decrease in oxidation.
CuO → Cu (decrease of 2 unit per atom)
NH3 → N2 (increase of 3 unit per atom)
Total decrease = 2 × 3 = 6
Total increase = 3 × 2 = 6
Step-3:
To balance the total decrease and increase in oxidation, multiply two by 3 and NH3 by 2. ’ .
3 CuO + 2NH3 → Cu + N2 + H2O
Step-4:
To balance all atoms other than ‘H’ and ‘O’
3 CuO + 2NH3 → 3Cu + N2 + H2O
Step-5:
To balance ‘O’ atoms
3 CuO + 2NH3 → 3Cu + N2 + 3H2O
hydrogen atoms balance by themselves.
Hence the final equation is
3CuO + 2NH3 → 3Cu + N2 + 3H2O
![]()
(ii) P + HNO3 →HPO3 + NO + H2O
Step-1:
To find atoms undergoing change in oxidation.
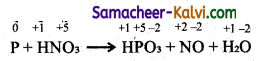
Step-2:
To find total decrease and increase in oxidation.
P → HPO3 (increase in O.N. of 5 units per atom)
HNO3 → NO (decrease in O.N. of 3 units per atom)
Total decrease 5 × 3 = 15
Total increase 3 × 5 = 15
Step-3:
To balance the total increase and decrease in the equation, by multiplying P by 3 and HNO3 by 5.
3P + 5HNO3 → HPO3 + NO + H2O
Step-4:
To balance all atoms other than ‘O’ and ‘H’
3P + 5HNO3 → 3HPO3 + 5NO + H2O
Step-5:
To balance by oxygen atoms Oxygen and hydrogen atoms balance by themselves.
Hence the balanced equation is
3P + 5HNO3 → 3HPO3 + 5 NO + H2O
![]()
(iii) KIO3 + SO2 + H2O → KHSO4 + H2SO4 + I2
Step-1: To find atoms undergoing change in oxidation.
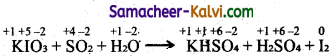
Step-2:
To find the total decrease and increase in oxidation.
KIO3 → I2 (decrease of 5 units per atom)
SO2 → H2SO4 (increase of 2 units per atom)
Total decrease = 5 × 2 = 10
Total increase = 2 × 5 = 10
Step-3:
To balance the total decrease and in oxidation increase, multiply KIO3 by 2 and SO2 by 5.
2 KIO3 + 5 SO2 + H2O → KHSO4 + H2SO4 + I2
Step-4:
To balance all atoms other than ‘O’ and ‘H’.
2 KIO3 + 5 SO2 + H2O → 2 KHSO4 + 3 H2SO4 + I2
Step-5:
To balance ‘O’ atoms 2 KIO3 + 5 SO2 + 4H2O → 2KHSO4 + 3H2SO4 + I2
Hydrogen atoms balance by themselves. Hence, the balanced equations is
2 KIO3 + 5SO2 + 4H2O → 2KHSO4 + 3H2SO4 + I2
(iv) C6H12O6 + H2SO4 → CO2 + SO2 + H2O
![]()
Step-1:
To find atoms undergoing change in oxidation.
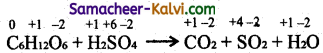
Step-2:
To find the total increase and decrease in oxidation.
C6H12O6 → CO2 (increase of 4 units per atom
Total increase = 24 units
H2SO4 → SO2 (decrease of 2 units per atom)
Total decrease = 2 x 12 = 24
Step-3:
To balance the total increase and decrease in oxidation, multiply H2SO4 by 12.
C6H12O6 + 12 H2SO4 → CO2 + SO2 + H2O
Step-4:
Balance all atoms other than ‘H’ and ‘O’
C6H12O6 + 12 H2SO4 → 6CO2 + 12SO2 + H2O
Step-5:
Balance ‘O’ atoms.
C6H12O6 + 12 H2SO4 → 6CO2 + 12SO2 + 18 H2O
Hydrogen atoms balance by themselves.
Hence the balanced equation is
C6H12O6 + 12 H2SO4 → 6CO2 + 12SO2 + H2O
(v) C4H10 + O2 → CO2 + H2O
![]()
Step-1:
To find atoms undergoing change in oxidation.
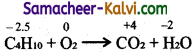
Step-2:
To find the total increase and decrease in oxidation.
C4H10 → CO2 + H2O (decrease by 6.5 units per atom)
– O2 → H2O (increases by 2 units per atom)
Step-2:
To find the total increase and decrease
Total decrease = 4 × 6.5 = 26 units in oxidation.
Total increase = 2 × 13 = 26
Step-3:
To balance the total increase and decrease in oxidation multiply C4H10 by 2 and O2 by 13.
2C4H10 + 13O2 → CO2 + H2O
Step-4:
To balance all atoms other ‘H’ and ‘O’.
2C4H10 + 13O2 → 8CO2 + H2O
Step-5:
To balance ‘O’ and ‘H’ atoms
2C4H10 + 13O2 → 8CO2 + 10H2O
hydrogen atoms balanced by themselves.
Hence balanced equations is
2C4H10 + 13O2 → 8CO2 + 10H2O
![]()
(vi) NH3 + F2 → HF + N2
Step – 1:
To find atoms undergoing change in oxidation.
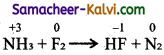
Step-2:
To find the total increase and decrease in oxidation.
NH3 → N2 (decrease of 3 units per atom)
F2 → HF (increase in 1 imit per atom)
Total decrease = 6 units (3 × 2)
Total increase = 6 units (2 × 3)
Step-3:
To balance the increase and decrease in oxidation, multiply NH3 by 2 and F2 by 3. 2NH3 + 3F2 → HF + N2
Step-4:
To balance all atoms other than oxygen
2NH3 + 3F2 → 6HF + N2
Hydrogen atom balanced by themselves.
Hence, the balanced equation is
2N3 + 3F2 → 6HF + N2
![]()
Question 54.
Balance the following equations by oxidation number method.
(i) K2Cr2O7 + HI → KI + CrI3 + H2O + I2
Answer:
Step-1:
To find atoms undergoing change in oxidation.
K2Cr2O7 + HI → KI + CrI3 + H2O + I2
Step-2:
To find the total increase and decrease in oxidation.
K2Cr2O7 + CrI3 (decrease of 3 unit / atom = Total decrease = 6 units / 2 atom)
HI → I2 (increase of 1 unit / atom = total increase 1 × 6 = 6)
Step-3:
To balance the total increase and decrease in oxidation, multiply HI by 6.
K2Cr2O7 + 6 HI → KI + CrI3 + H2O + I2
Step-4:
To balance all atoms other than ‘O’ and ‘H’
K2Cr2O7 + 6 HI → 2KI + 2CrI3 + H2O + 3I2
This makes 14 iodine atoms on RHS. (These iodide ions do not undergo any change in oxidation). Hence to balance the iodine atoms
add 8HI to LHS
i.e.,K2Cr2O7 + 14 HI → 2KI + 2CrI3 + H2O + 3I2
These, the oxygen atoms are balanced by making 7H2O as RHS.
K2Cr2O7 + 14HI → 2KI + 2CrI3 + 7H2O + 3I2
The hydrogen atoms are balanced by themselves.
Hence the balanced equation is
K2Cr2O7 + 14HI → 2KI + 2CrI3 + 7H2O + 3I2
![]()
(ii) Zn + HNO3 → Zn(NO3)2 + N2O + H2O.
Step-1:
To find out atoms undergoing change in oxidation.
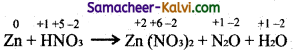
Step-2:
To find out the total increase and decrease in O.N.

Total increase 2 × 4 = 8
Total decrease 4 × 2 = 8
Step-3:
To balance the total increase and decrease in oxidation.
4Zn + 2HNO3 → Zn(NO3)2 + N2O + 5H2O
Step-4:
Balance the equation
4Zn + 2HNO3 → 4Zn(NO3)2 + N2O + 5H2O
‘8’ nitrogen atoms, 12 oxygen atoms ‘8’ hydrogen atoms in RHS to be balanced.
For this add 8 HNO3 to LHS.
4Zn + 10HNO3 → 4Zn(NO3)2 + N2O + 5H2O
The equation is now balanced.
![]()
(iii) Ag + HNO3 → AgNO3 + H2O + NO
Answer:
Step-1:
To balance atoms undergoing change in oxidation.
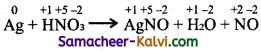
Step-2:
To find out total increase and decrease in oxidation.

Total increase =1 × 3 = 3
Total decrease = 3 × 1 = 3
Step-3:
To balance the total increase and decrease in oxidation, multiply Ag by 3.
3Ag + HNO3 → AgNO3 + H2O + NO
Step-4:
To balance all atoms other than hydrogen and oxygen.
3 Ag + 4HNO3 → 3 AgNO3 + H2O + NO
Step-5:
To balance oxygen atoms
3 Ag + 4HNO3 → 3 AgNO3 + 2H2O + NO
Hydrogen atoms balanced by themselves.
The balanced equation is ,
3Ag + 4HNO3 → 3AgNO3 + 2H2O+ NO
![]()
(iv) K2Cr2O7 + FeSO4 + H2SO4 → K2SO4 + Cr2(SO4)3 + Fe2(SO4)3 + H2O
Answer:
Step-1:
To find out atoms undergoing change in oxidation.
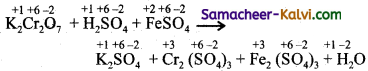
Step-2:
To find out total increase and decrease in oxidation.
+6 +3
K2Cr2O7 → Cr2(SO4)3 (Decrease of 3 unit / atom ; 6 unit / 2 atoms)
Total decrease = 6 units
+2 +3
Fe2(SO4) → Fe2(SO4)3 (increase of 1 unit / atom)
Total increase 1 × 6 = 6
Step-3:
To balance the total increase and total decrease, multiply FeSO4 by 6.
K2Cr2O7 + 6FeSO4 + H2SO4 → K2SO4 + Fe2(SO4)3 + Cr2(SO4)3 + H2O
Step-4:
Balance all atoms other than ‘H’ and ‘O’.
Since Fe is oxidised (LHS) to Fe+3 (RHS) balance Fe2(SO4)3 by multiplying by 3.
Now the equation becomes,
K2Cr2O7 + 6FeSO4 + H2SO4 → K2SO4 + Cr2(SO4)3 + 3 Fe2(SO4)3 + H2O
The sulphur atoms in SO4-2 radical does not undergo any change in O.N. There are 7, SO2-2 radicals in LHS and 13, SO4-2 radicals in RHS. To balance them, multiply H2SO4 in LHS by 7.
The equation now becomes
K2Cr2O7 + 6FeSO4 + 7H2SO4 → K2SO4 + Cr2(SO4)3 + 3 Fe2(SO4)3 + 7H2O
To balance, ‘H’ atoms multiply H2O molecules in RHS by 7.
K2Cr2O7 + 6FeSO4 + 7H2SO4 → K2SO4 + Cr2(SO4)3 + 3 Fe2(SO4)3 + 7H2O
This is the balanced equation.
![]()
(v) KBr + MnO2 + H2SO4 → KHSO4 + MnSO4 + H2O + Br2
Answer:
Step-1:
To find atoms undergoing change in oxidation.
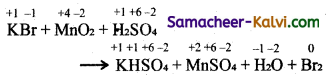
Step-2:
To find the total increase and decrease
+4 +2
MnO4 → MnSO4 (Decrease in O.N. of 2 units per atom)
KBr-1 Br2 (increase in O.N. of 1 unit per atom)
Total decrease = 2 × 1 = 2
Total increase = 1 × 2 = 2
Step-3:
To balance the total increase and decrease in oxidation, multiply KBr by 2.
2KBr + MnO2 + H2SO4 → KHSO4 + MnSO4 + H2O + Br2
Step-4:
To balance all atoms other than hydrogen and oxygen atoms
2KBr + MnO2 + H2SO4 → 2KHSO4 + MnSO4 + H2O + Br2
Since SO4-2 (sulphate) radical does not undergo any change in oxidation.
balance them RHS = 3 (SO4-2) radical .
RHS = 1 (SO4-2)
Hence multiply H2SO4 in LHS by 3. The equation now becomes
2KBr + MnO2+ 3H2SO4 → 2KHSO4 + MnSO4 + H2O + Br2
To balance ‘O’ atoms, multiply H2O in RHS by 2.
2KBr + MnO2 + 3H2SO4 → 2KHSO4 + MnSO4 + 2H2O + Br2
This is the balanced equation.
![]()
(vi) KMnO4 + KOH + H2O2 → K2MnO4 + O2 + H2O
Answer:
Step-1:
To find out atoms undergoing change in oxidation.
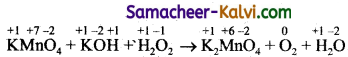
Step-2:
To find out total increase and decrease in oxidation.
+ 7 +6
KMnO4 → K2MnO4 (decrease of 1 unit per atom)
-1 0
H2O2 → O2 (increase of 1 unit per atom or 2 units per atom)
Total decrease = 2
Step-3:
To balance the total increase and decrease in 0.N, multiply KMnO4 by 2.
2KMnO4 + KOH + H2O2 → K2MnO4 + O2 + H2O
Step-4:
To balance all atoms other than ‘H’ and ‘O’
2KMnO4 + 2KOH + H2O2 → 2K2MnO4 + O2 + H2O
number of oxygen atoms on LHS = 12
number of oxygen atoms on RHS = 11
Hence, multiply H2O in RHS by 2. The equation becomes,
2KMnO4 + 2KOH + H2O2 → 2K2MnO4 + O2 + H2O
Hydrogen atoms balance by themselves.
The balanced equation is
2KMnO4 + 2KOH + H2O2 → 2KMnO4 + O2 + 2H2O
![]()
Question 55.
Balance the following equation by ion electron method.
(i) Cr2O72- + Fe2+ → Cr3+ + Fe2+ in acidic medium.
Answer:
Cr2O7-2 → Cr+3 (reduction) (The O.N of Cr decreases from +6 to +3)
Fe+2 → Fe+3 (oxidation) (The O.N of Fe increases from +2 to +3)
Balancing oxidation and reduction half reactions separately.
Cr2O7-2 → Cr+3
Fe+2 → Fe+3
Step-1:
Balance all atoms, other than hydrogen and oxygen.
Cr2O7-2 → 2Cr+3
Fe+2 → Fe+3
Step-2:
Balance oxygen atom by adding equal number of H2O molecules on the side deficient of oxygen.
Cr2O7-2 → 2Cr+3 + H2O
Fe+2 → Fe+3.
Step-3:
To balance, hydrogen atom in acidic medium, add equal number of H+ ions on the side deficient of hydrogen atom.
14H+ + Cr2O7-2 → 2Cr+3 + 7H2O
Fe+2 → Fe+3
Step-4:
Balance the charges in such a way the charges on either side be the same,
6e + Cr2O7-2+ 14H+ → 2Cr+3 + 7H2O
Fe+2 → Fe+3
Add both equations in such a way the number of electrons taken up by the oxidising agent and the number of electron given by the reducing agent be the same,
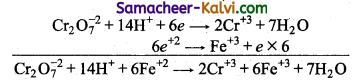
![]()
(ii) Cr2O7-2 + C2H4O → Cr3+ + C2H4O2 in acidic medium.
Answer:
Cr2O7-2 → Cr+3 (Reduction)
C2H4O → C2H4O2 (Oxidation)
Step-1:
Balance all atoms other than oxygen
Cr2O7-2 → 2Cr+3
C2H4O → C2H4O2
Step-2:
Balance oxygen atom by adding water molecules on the side deficient of oxygen atom.
Cr2O7-2 → 2Cr+3 + H2O
C2H4O + H2O → C2H4O2
Step-3:
To balance, hydrogen atom in acidic medium, add equal number of H+ ions on the side deficient of hydrogen atom.
Cr2O7-2 + 14 H-1 → 2Cr+3 + H2O …………….(1)
C2H4O + H2O → C2H4O2 + 2H+ + 2e ……….(2)
Multiply equation (2) by 3 and add with equation (1)
Cr2O7-2 + 14 H+ + 6e → 2 Cr+3 + H2O
C2H4O + H2O → C2H4O2 + 2H+ + 2e × 3
Cr2O7-2 + C2H4O + 8H+ → 2 Cr+3 + 4 H2O + 3 C2H4O2
![]()
(iii) Zn + NO3– → Zn+2 + NH4 in basic medium.
Zn → Zn+2 + 2e (oxidation)
NO3– → NH4+ (Reduction)
Answer:
Step-1:
Balance all atoms other than hydrogen and oxygen.
Zn → Zn+2
NO3– → NH4+
Step-2:
For balancing oxygen atom in alkaline medium, add H2O molecules on the side deficient of oxygen atom. Then balance hydrogen atom, add H2O molecule to file side deficient in hydrogen and equal number of ,OH– on the other side.
Zn → Zn+2
NO3– → NH4+ + 3H2O
NO3– + 10H2O → NH4+ + 3H3O
NO3– + 10H3O → NH4+ + 3H2O + 10 OH–
Step-3:
Add electrons to balance charge
Zn → Zn+2 + 2e
NO3– + 7H2O + 8e → NH4+ + 10 OH–
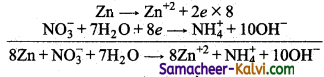
This is the balanced equation.
![]()
Question 56.
The approximate production of Na2CO3 per month is 424 × 106 g while that of methyl alcohol is 320 × 106 g. Which is produced more in terms of moles?
Answer:

Gram molecular weight of methyl alcohol (CH3OH) = 32g
number of mol of methyl alcohol = \(\frac{320 \times 10^{6}}{32}\)
= 10 × 106 mol.
Hence methyl alcohol is produced move in terms of moles.
Question 57.
Calculate the number of moles of carbon atoms in three moles of ethane.
Answer:
Ethane = Molecular formula C2H6
1 mol of ethane = 2 mol of carbon atoms
3 mol of ethane = 2 × 3 mol of carbon atoms = 6 mol.
![]()
Question 58.
Find the molecular mass of FeSO47H2O.
Answer:
Molecular mass is the sum of atomic masses of various atoms present in one molecule of the compound.
FeSO47H2O:
Atomic mass of Fe = 55.85
Atomic mass of S = 32
Atomic mass of O = 16
Atomic mass of H = 1
Molecular mass of 7H2O = 7 × 18 = 126
Molecular mass of FeSO4.7H2O = 55.85 + 32 + 4 × 16 + 126
= 277.854 = 278 u
Question 59.
Mass of one atom of an element is 6.66 × 10-23 g. How many moles of element are there in 0.320kg?
Answer:
No. of mol = (Weight of the substance in gram) / Gram molecular mass.
Step -1:
Find the gram molecular weight of the atom.
Mass of 6.023 × 1023 atoms = 1 mole = 1 gram molecular weight
Mass of one atom of the element = 6.626 × 10-23 g
Mass of 6.023 × 1023 atoms = 6.626 × 10-23 × 6.023 × 1023 = 40.1 .
Therefore, the gram molecular weight of the element is 40.1 g
Step -2:
To find the number of. mol in 0.320 kg
Number of mol = \(\frac{0.320 \times 1000 g}{40.1 g}\)
= 7.98 ≈ 8 mol
![]()
Question 60.
The density of CO2 = 1.977kgm-3 at STP. Calculate the molecular mass of CO2.
Answer:
Density of CO2 = 1.977 kg m-3
This means 1m3 of CO2 weighs 1.977 kg.
22.4 L (or) 22.4 × 10-3 m-3 = 1.977 × 22.4 × 10-3 kg
Weigh = 1.977 × 22.4 × 10-3 × 103 g
= 44.28g = 44.28 u.
The molecular mass of CO2 is the mass of 22.4 L or 22.4 × 10~3 m3 of CO2.
Question 61.
How many moles of glucose are present in 720 g of glucose?
Answer:
The Molecular formula of glucose: C6H12O6
Molecular mass of glucose = 6 × 12 + 12 + 6 × 16] = 72 + 12 + 96 = 180M.
180 g of glucose = 1 mol
720 g of glucose = \(\frac{1 \times 720}{180}\) = 4 mol
Question 62.
Calculate the weight of 0.2 mole of sodium carbonate.
Answer:
Moleular formula of sodium carbonate = Na2CO3
Molecular mass of sodium carbonate = 2 × 23 + 12 + 3× 16
= 46 + 12 + 48 = 106 u
1 mol of Na2CO3 = 106 grams
0.2 mol of Na2CO3 = 106 × 0.2 gram = 21.2g
![]()
Question 63.
Calculate the equivalent mass of bicarbonate ion.
Answer:
Equivalent mass of an ion = (sum of atomic mass of constituent atom in an ion) / charge on the ion
Bi-carbonate ion has the formula HCO3–.
Equivalent mass ofl carbonate ion = (atomic mass of hydrogen atom + atomic mass of carbon atom + 3 × atomic mass of oxygen atom) / (charge on bi – carbonate ion)
= \(\frac{1+12+3 \times 16}{1}=\frac{1+12+48}{1}\) = 61
The equivalent mass of carbonate ion is 61 g. eq-1
Question 64.
Calculate the equivalent mass of barium hydroxide.
Answer:
Barium hydroxide has the formula Ba(OH)2.
Molecular mass of barium hydroxide = atomic mass of Ba atom + 2 × atomic mass of oxygen atom + 2 × atomic mass of hydrogen atom
= 137.27 + 2 × 16 + 2 × 1
= 137.27 + 32 + 2 = 171.27
Equivalent mass of barium hydroxide = (Molecular mass) / (No. of ‘OH’ group present)
= \(\frac{171.27}{2}\) = 85.64 g. eq-1.
![]()
Question 65.
Calculate the equivalent mass of hydrated sodium carbonate.
Answer:
Hydrated sodium carbonate has the formula Na2CO3.10H2O
Molecular mass of Na2CO3.10H2O = 2 × atomic mass of Na + 1 × atomic mass of C + 3 × atomic mass of oxygen + 10 × molar mass of H2O
= 2 × 23 + 12 + 3 × 16 + 10 × 18 = 46+ 12 + 48 + 180 = 286u
2 NaOH + H2CO3 → Na2CO3 + 2H2O
Equivalent mass of NaOH = Molar mass of NaOH
2 equivalent of NaOH = 1 equivalent of Na2CO3
1 equivalent of NaOH = \(\frac{1}{2}\) equivalent mass of Na2CO3
Equivalent mass = \(\frac{\text { Molar mass }}{2}\)
= \(\frac{286}{2}\) = 143 g eq-1
Question 66.
Boric acid, H3BO3 is a mild antiseptic and is often used as an eye wash. A sample contains 0.543 mol H3BO3. What is the mass of boric acid in the sample?
Answer:
Molecular formula of boric acid = H3BO3
Molecular mass of boric acid = 3 × atomic mass of hydrogen atom + atomic mass of boron atom + 3 × atomic mass of oxygen atom
= 3 × 1 + 10.8 + 3 × 10
= 3 + 10.8 + 48 = 80.4u.
1 mol of boric acid = 80.4 gram
0.543 mol = \(\frac{80.4}{1}\) = 43.6g
Remember the formula:
Number of mol of a substance = (Weight of the sample in gram) / gram molecular mass
![]()
Question 67.
A compound contains 50 % of X (atomic mass 10) and 50 % Y (atomic mass 20).Give its molecular formula.
Answer:
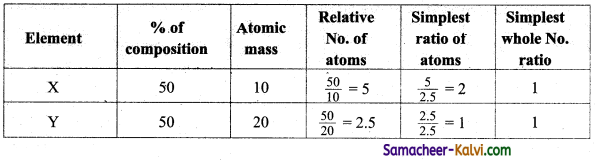
Empirical formula = XY.
Molecular formula can be calculated one of the molecular mass of the compound is given by using the formula.
Molecular mass = (Empirical formula mass)n
Molecular formula = (Empirical formula)n
Where n = \(\frac{\text { Molecular mass }}{\text { Empirical formula mass }}\)
If the molecular mass is assured to be equal to 20. Then, the molecular formula of the compound is XY.
Question 68.
Calculate the mass of sodium (in kg) present in 95 kg of a crude sample of sodium nitrate whose percentage purity is 70%.
Answer:
Mass of impure sample of sodim nitrate (NaNO3) = 95 × 1000 g
Mass of pure sample of sodium nitrate (NaNO3) = 95 × 1000 × \(\frac{70}{100}\)
= 66500 g
1 mole of pure NaNO3 = 85 g
85 g NaNO3 = 23 g of Na
66,500 of NaNO3 = \(\frac{23}{85}\) × 66500 g of NaNO3
= 17994.1 gram = 17.99 kg
![]()
Choose the correct answer:
Question 1.
Which one of the following is the standard for atomic mass?
(a) 1H1
(b) 6C12
(c) 6C14
(d) 8O16
Answer:
(b)
Hint:
If 1H1 is used as a reference, the atomic mass is expressed in hydrogen scale and 8O16 is used as a reference the atomic mass is expressed in oxygen scale 6C12 is used as a standard atom and atomic mass is expressed in C-12- scale.
Question 2.
One mole of CO2 contains:
(a) 6.023 × 1023 atoms of C
(b) 6.023 × 1023 atoms of O
(c) 18.1 × 1023 molecules of CO2
(d) 3g atoms of CO2
Answer: (a)
Hint: 1 mole of CO2 = 1 mole of C = 2 mole of ‘O’ atoms
= 6.023 × 1023 atoms of carbon
= 2 × 6.023 × 1023 atoms of oxygen
= 6.023 × 1023 molecules of CO2
![]()
Question 3.
The largest number of molecules is in:
(a) 54 g of nitrogen pentoxide
(b) 28 g of carbon dioxide
(c) 36 g of water
(d) 46 g of ethyl alcohol
Answer: (a)
Hint:
N2O5: Molar mass =108
108 g N2O5 = 1 mol
= 6.023 × 1023 molecules.
54g of N2O5 = \(\frac{6.023 \times 10^{23}}{108}\) × 54
= 3.012 × 1023 molecules
CO2: Molar mass = 44.
44g of CO2 = 1 mol
= 6.023 × 1023 molecules
28g of CO2 = \(\frac{6.023 \times 10^{23}}{44}\) × 28
= 0.636 × 6.023 × 1023 mol
H2O: Molar mass = 18.
18g of H2O – 1 mol = 6.023 × 1023 molecules
36g H2O = 2mol
= 2 × 6.023 × 1023 molecules
C2H5 OH: Molar mass = 46
46g = 1 mol
= 6.023 × 1023 molecules
![]()
Question 4.
The number of moles of H2 in 0.224 litre of hydrogen gas at STP is:
(a) 1
(b) 0.1
(c) 0.01
(d) 0.001
Answer: (c)
Hint: 22.4 L of H2 at STP = 1 mol of H2O
0.224 L of H2 at STP = \(\frac{1 \times 0.224}{22.4}\) = 0.01 mol
Question 5.
10 g of hydrogen and 64 g of oxygen were filled in a steel vessel and exploded. The amount of water produced in this reaction will be:
(a) 3 mol
(b) 4 mol
(c) 1 mol
(d) 2 mol
Answer: (b)
Hint:
2H2 + O2 → 2H2O
10 g of H2 = \(\frac{10}{2}\) = 5 mol of H2
64 g of O2= \(\frac{1}{12}\) = 2 mol of O2
1 mol of O2 = 2 mol of H2 as per equation .
2 mol of O2 = 4 mol of H2
i.e., one mol of H2 remain excess.
O2 of the limiting reagent
1 mol O2 = 2 mol H2O
2 mol O2 = 4 mol H2O
![]()
Question 6.
6.023 × 1020 molecules of urea are present in 100 ml of its Solution. The concentration of the solution is:
(a) 0.02 M
(b) 0.1 M
(c) 0.01 M
(d) 0.001 M
Answer: (c)
Hint: Molarity is defined by the number of mol of solute present in 1L of the solutions.
Molarity = \(\frac{\text { no. of mole of the solute } \times 1000}{\text { Volume of solution in } \mathrm{cm}^{3}}\)
6.023 × 1023 molecule of urea = 1 mol
6.023 × 1020 molecules of urea
= \(\frac{1 \times 6.023 \times 10^{20}}{6.023 \times 10^{23}}\)
= 10-3 mol
∴ molarity = \(\frac{10^{-3} \times 1000}{100}\) = 0.01 M
Question 7.
Two containers A and B of equal volume contain 6g of each O2 and SO2 at 300K and latm. Then:
(a) No. of molecules in A is less than that in B
(b) No.of molecules in A is more than that in B
(c) No. of molecules in A and B are same
(d) none of these
Answer: (b)
Hint: 6g O2 = \(\frac{6}{32}\) =0.1875 mol
6g SO2 = \(\frac{6}{64}\) = 0.0934 mol
At a given temperature and pressure, number of mole is proportional to number of molecule.
Here (b) is the correct option.
![]()
Question 8.
The number of molecules in 16g of methane is:
(a) 3.023 × 1023
(b) 6.023 × 1023
(c) 16/6.023 × 1023
(d) 6.023/3 × 1023
Answer: (b)
Hint: CH4:
Molar mass = 16g mol-1
16g methane = 1 mol
= 6.023 × 1023 molecules
Question 9.
No. of atoms in 4.25g of ammonia is:
(a) 1 × 1023
(b) 2 × 1023
(c) 4 × 1023
(d) 6 × 1023
Answer: (d)
Hint:
1 mol of NH3 = (3 mol of hydrogen + 1 mol of nitrogen) = 4 mol of atoms
4.25g of NH3 = \(\frac{4.25}{17}\) = 0.25 mol of N3
1 mol of NH3 = 4 × 6.023 × 1023 atom
0.25 mol NH3 = \(\frac{4 \times 6.023 \times 10^{23}}{1}\) × 0.25
= 6.023 × 1023 atom
![]()
Question 10.
The number of molecules in a drop of water (0.0018mL) at room temperature is: •
(a) 6.02 × 1019
(b) 1.084 × 1018
(c) 4.84 × 1017
(d) 6.02 × 1023
Answer: (a)
Hint:
0.0018ml of H2O = 0.0018g H2O
(density of H2O) = 1g / cc
18g H2O = 1 mol
= 6.023 × 1023 molecules
0.0018g of H2O = \(\frac{6.023 \times 10^{-23} \times 0.0018}{18}\)
= 6.023 × 1023 × 10-4
= 6.023 ×1019 molecule
Question 11.
7.5g of a gas occupy 5.6 litres of volume at STP. The gas:
(a) NO
(b) N2O
(c) CO
(d) CO2
Answer: (a)
Hint: 1 mol of gas at NTP will occupy 22.4L at 1 mol is molecular weight expressed in grams
5.6L of gas at STP = 75 g
22.4L of the gas at STP = \(\frac{7.5}{5.6}\) × 22.4 g = 30 g
i.e. The molecular weight of the gas is 30.
NO = Molar mass = 30
N2O = Molar mass = 44
CO = Molar mass = 28
CO2 = Molar mass = 44
![]()
Question 12.
The mass in grams of 0.45 mole of Ca2+ ions:
(a) 1.8
(b) 40
(c) 36
(d) 18
Answer: (d)
Hint: Ca and Ca+ ion have the same atomic mass, i.e. 40.
1 mol of Ca+2 = 40g
0.45 mol of Ca+2 = 40 × 0.45 = 18g
Question 13.
The mass of one molecule of HI in grams is:
(a) 2.125 × 10-22
(b) 128
(c) 127
(d) 6.02 × 10-23
Answer: (a)
Hint: Molecular mass of HI = 1 + 127 = 128
6.023 × 1023 molecules of HI = 128 g
1 molecule of HI = \(\frac{128}{6.023 \times 10_{4}^{23}}\)
= 21.25 × 10-23
= 2.125 × 10-23
![]()
Question 14.
Avogadro’s number is the number of molecules present in:
(a) 1 g of molecule
(b) 1 g atom of molecule
(c) gram molecular mass
(d) 1 lit of molecule
Answer: (c)
Hint: Gram molecular mass is the molecular mass expressed in grams which correspond to one mol of the molecule. The number of molecules present in one mole of the substance is known as the Avogadro number.
Question 15.
Which of the following contains same number of carbon atoms as are in 6.0 g of carbon (C – 12)?
(a) 6.0 g ethane
(b) 8.0 g methane
(c) 21.0 g Propane
(d) 28.0 g CO
Answer: (b)
Hint: 6g of carbon = \(\frac{6}{12}\) = 0.5 mol.
The given choice should contain 0.5 mol of carbon atoms.
6g of ethane (C2H6) = \(\frac{6}{30}\) = 0.2 mol
(a) 1 mol of ethane = 2 mol of carbon atoms
0.2 mol = 2 × 0.2 × 6.023 × 1023 carbon atoms
= 0.4 × 6.023 × 1023 carbon atoms
(b) 1 mole of methane = 1 mol of carbon atom
8g of methane = \(\frac{8}{16}\) = 0.5 mol
∴ 0.5 mol of methane = 0.5 mol of carbon atom
(c) 21g of propane = \(\frac{21}{44}\) = 0.477 mol.
1 mol of C3H8 = 3 mol of carbon atoms
0.477 mol of C3H8 = 3 × 0.477
= 1.432 mol of carbon atom
(d) 28g of CO = 1 mol = 1 mol of CO.
Hence 6g of carbon and 8g of methane contain same number of carbon atoms.
![]()
Question 16.
Equivalent mass of KMnO4 when it is converted to MnSO4 is equal to molar mass divided by:
(a) 6
(b) 4
(c) 5
(d) 2
Answer: (c)
Hint: MnO4– → Mn+2
MnO4– + 8H+ + 5e Mn+2 + 4H2O
Equivalent mass = (Molar mass) / (no. of e– involved in half reaction)
= M / 5
Question 17.
How many equivalents of sodium sulphate is formed when sulphuric acid is completely neutralized by a base NaOH:
(a) 0.2
(b) 2
(c) 0.1
(d) 1
Answer: (b)
Hint: 2NaOH + H2SO4 → Na2SO4 + 2H2O
1 mol of H2SO4 = 2 equivalent of H2SO4
.’. 2 equivalent of H2SO4 will form 2 equivalent of Na2SO4
Note:
One equivalent of any substance will always react with one equivalent of any other substance and one equivalent of the product.
![]()
Question 18.
Cl2 changes to Cl– and ClO– in cold NaOH. Equivalent mass of Cl2 will be:
(a) Molar mass/2
(b) Molar mass/1
(c) Molar mass/3
(d) 2 × Molar mass/2
Answer: (a)
Hint: (Reduction)
Cl2 → Cl–
Cl2 → 2Cl–
Cl2 + 2e → 2Cl–
(Oxidation)
Cl2 → 2OCl–
Cl2 + 4 0H– → 2H2O + 2OCl– + 2e
Cl2 + 2e → 2Cl–
Cl2 + 2OH– → Cl + OCl– + H2O
Since this is a 2 electron transfer reaction equivalent mass of chlorine is \(\frac{M}{2}\).
![]()
Question 19.
Equivalent mass of KMnO4 in acidic medium, concentrated alkaline medium and dilute basic medium respectively are \(\frac{M}{5}\), M, M. Reduced products can be:
(a) MnO2, MnO4–, Mn2+
(b) MnO2, Mn2+, MnO42-
(c) Mn2+, MnO2, MnO42-
(d) Mn2+, MnO42-, MnO2
Answer: (d)
Hint: KMnO4 (MnO4–) acts as an oxidising agent in acidic alkaline and in neutral medium. The half reactions are:
MnO4– + 8H+ 5e → Mn+2 + 4 H2O(acidic)
Equivalent mass = \(\frac{\text { Molar mass }}{5}\)
MnO4– + e → MnO4-2 (alkaline)
Equivalent mass = Molar mass
MnO4– + 2H2O + 3e → MnO2 + 4 OH– (neutral or mild alkaline)
Equivalent mass = \(\frac{\text { Molar mass }}{3}\)
![]()
Question 20.
The empirical formula of hydrogen peroxide is:
(a) HO
(b) H2O
(c) H3O+
(d) H2O2
Answer: (a)
Hint: The formula of hydrogen peroxide is H2O2. Its simplest formula is HO.
Question 21.
Molecular mass =
(a) Vapour Density × 2
(b) Vapour Density ÷ 2
(c) Vapour Density × 3
(d) Vapour Density
Answer: (a)
![]()
Question 22.
20.0 g of a magnesium carbonate sample decomposes on heating to give carbon dioxide and 8.0 g magnesium oxide. What will be the percentage of purity of magnesium carbonate in the sample?
(a) 60
(b) 84
(c) 75
(d) 96
Answer: (b)
Hint: MgCO3 → MgO + CO2
24.3 + 12 + 48 = 84.3 g 24.3 + 16 = 40.3 g
40.3 g MgO = 84.3 g MgCO3
8 g MgO = \(\frac{84.3}{40.3}\) × 8 = 16.7 g
Percentage of purity = \(\frac{16.7}{20}\) × 100 = 83.67 % ≈ 84 %
Question 23.
What is the mass of the precipitate formed when 50 mL of 16.9% solution of AgNO3 is mixed with 50 mL of 5.8% NaCl solution?
(a) 7 g
(b) 14 g
(c) 28 g
(d) 35 g
Answer: (a)
Hint:AgNO3 + NaCl → AgCl + NaNO3
Molarity of AgNO3 = \(\frac{\text { weight of } \mathrm{AgNO}_{3}}{\text { gram molecular weight }} \times \frac{1000}{\text { volume in } \mathrm{cm}^{3}} \text {. }\)
= \(\frac{16.9}{170} \times \frac{1000}{50}\) ≈ 2 M
Molarity of NaCl = \(\frac{16.9}{170} \times \frac{1000}{50}\) ≈ 1 M
No. of mol. of AgNO3 = \(\frac{\mathrm{M} \times \text { Volume in } \mathrm{cm}^{3}}{1000}\)
= \(\frac{2 \times 50}{1000}\) 1 M
No. of mol of NaCl = \(\frac{1 \times 50}{1000}\) = 0.05 M
NaCl is the limiting reagent.
∴ No. of mol of AgCl formed = 0.05 M
Mass of AgCl formed = 0.05 × 143.58 = 7.188 g ≈ 7 g
![]()
Question 24.
When 22L of hydrogefo gas is mixed with 11.2 L of chlorine gas, each at STP, the moles of HCl gas formed is equal to:
(a) 2
(b) 0.5
(c) 1.5
(d) 1
Answer: (a)
Hint:. H2 + Cl2 → 2HCl
Chlorine is the limiting reagent.
11.2L of chlorine will form 2 mol of HCl as per equation.
Question 25.
5.6 L of a gas at STP are found to have mass of 11 g. The molecular mass of the gas is:
(a) 36
(b) 48
(c) 40
(d) 44
Answer: (d)
Hint: 5.6L of the gas = 11 g
22.4 L of the gas = \(\frac{1}{12}\) × 22.4 = 44g .
Hence the Molar mass of the gas is 44.
![]()
Question 26.
Oxidation number of Fluorine in all compounds is:
(a) +1
(b) – 1
(c) 0
(d) – 2
Answer: (b)
Question 27.
In redox reaction which of the following is true?
(a) Number of electrons lost is more than number of electrons gained
(b) Number of electrons lost is less than number of electrons gained
(c) Number of electrons lost is equal number of electrons gained
(d) No transfer and gain of electrons during the reaction.
Answer: (c)
Question 28.
Match the entities in column I with appropriate entities in column II.
| Column I | Column II |
| (No. of moles) | (Amount) |
| (i) 0.1 mole | (A) 1.5 x 1023 molecules of oxygen gas |
| (ii) 0.2 mole | (B) 0.1 g atom of iron |
| (iii) 0.25 mole | (C) 9 ml of water |
| (iv) 0.5 mole | (D) 4480 ml of CO, at STP |
(a) (i) – (B), (ii) – (D), (iii) – (A), (iv) – (C)
(b) (i) – (D), (ii) – (A), (iii) – (C), (iv) – (B)
(c) (i) – (D), (ii) – (A), (iii) – (B), (iv) – (C)
(d) (i) – (C), (ii) – (A), (iii) – (D), (iv) – (B)
Answer: (a)
![]()
Question 29.
Match the entities in column I with appropriate entities in column II.
| Column I (Mass of the substance) | Column II
(Number of molecules) |
| (i) 54g of N205 | (A)3.8 × 10 |
| (ii) 28g of C02 | (B) 6.023 × 1023 |
| (iii) 36g of H20 | (C)3.012 × l023 |
| (iv) 46g of ethyl alcohol (C2H5OH) | (D) 1.2 × l024 |
(a) (i) – (B), (ii) – (D), (iii) – (A), (iv) – (C)
(b) (i) – (D), (ii) – (A), (iii) – (C), (iv) – (B)
(c) (i) – (D), (ii) – (A), (iii) – (B), (iv) – (C)
(d) (i) – (C), (ii) – (A), (iii) – (D), (iv) – (B)
Answer: (d)
Question 30.
In the following questions one of the option is different from the rest.
(a) 40 g of NaOH in 1L of H2O
(b) 98 g of H2S04 in 1L of H2O
(c) 58.5 g of NaCl in 1L of H2O
(d) 98% H2SO4 by mass, which has a density of 1.84 g cm3.
Answer: (d)
Hint:
All (a),(b),(c) represent a 1 molar solution of that substance while (d) has the molality of 18.4.
98 % H2SO4 by mass means 98 g of H2SO4 are present in 100 g of the solution.
= \(\frac{100 g}{1.84 g \mathrm{~cm}^{3}}\) = 0.5435 L
Mass of H2SO4 = 98 g mol-1 = 1 mole
Molarity of the given solution = \(\frac{1 \mathrm{~mol}}{0.5345 \mathrm{~L}}\) = 18.4 M
![]()
Question 31.
In the following questions one of the option is different from the rest.
(a) Air
(b) Brass
(e) An aqueous solution of sugar
(d) Petrol
Answer: (d)
Hint: While (a),(b),(c) are homogeneous mixture, (d) is a heterogeneous mixture.
Question 32.
From the following, choose the correct pair of diatomic molecules.
(a) Copper and hydrogen
(b) Copper and phosphorus
(c) Nitrogen and oxygen
(d) Oxygen and Sulphur
Answer: (c)
Hint: Copper is mono atomic (Cu), hydrogen is diatomic (H2), phosphorus and sulphur are poly atomic. N2 and O2 are diatomic.
![]()
Question 33.
Which of the following pairs of the solutions contain same number of mol of the solute?
(a) 500 ml of 1M solution of NaOH and 1000 ml of 0.5 M solution of NaOH.
(b) 500 ml of 1M solution of NaOH and 100 ml of 0.1 M solution of NaOH.
(c) 500 ml of 0.1 M solution of NaOH and 100 ml of 0.5 M solution of NaOH.
(d) 1000 ml of 0.5M solution of NaOH and 100 ml of 0 .1 M solution of NaOH.
Answer: (c)
Hint:
No. of moles = \(\frac{\mathrm{M} \times \mathrm{vol} \mathrm{in} \mathrm{cm}^{3}}{1000}\)
= \(\frac{0.1 \times 500}{1000}=\frac{50}{1000}\) = 0.05
= \(\frac{0.5 \times 100}{1000}\) = 0.05
Question 34.
Statement 1:
A single C12 atom has a mass exactly 12 amu and a mole of these atoms has a mass of exactly 12 grams. .
Statement 2:
A mole of atoms of any element has a mass in grams equal to its atomic mass.
(a) Statement (1) is true, Statement (2) is true, Statement (2) is the correct explanation for Statement (1).
(b) Statement (1) is true, Statement (2) is true, Statement (2) is not a correct explanation for Statement (1).
(c) Statement (1) is true, Statement (2) is false.
(d) Statement (1) is false, Statement (2) is true.
Answer: (a)
![]()
Question 35.
Statement 1:
In a gaseous reaction, the ratio of volumes of reactants – and gaseous products is in agreement with their molar ratio.
Statement 2:
Volume of a gas is inversely proportional to its moles at a particular temperature and pressure.
(a) Statement (1) is true, Statement (2) is true, Statement (2) is the correct explanation for Statement (1).
(b) Statement (1) is true, Statement (2) is true, Statement (2) is not a correct explanation for Statement (1).
(c) Statement (1) is true, Statement (2) is false.
(d) Statement (1) is false, Statement (2) is true.
Answer: (c)
Hint: Correct Statement (2):
Volume of a gas is directly proportional to its moles at a particular temperature and pressure.
Question 36.
Statement 1:
Both 100 g of sodium carbonate and 12g of carbon have the same number of carbon atoms.
Statement 2:
Both contain lg atom of carbon which contains 6.023 × 1023 carbon atoms
(a) Statement (1) is true^Statement (2) is true, Statement (2) is the correct explanation for Statement (1).
(b) Statement (1) is true, Statement (2) is true, Statement (2) is not a correct explanation for Statement (1).
(c) Statement (1) is true, Statement (2) is false.
(d) Statement (1) is false, Statement (2) is true.
Answer: (a)
Hint:
106g Na2CO3 = 1 mol = 1 g atom of C
12g C = 1 g atom of C
![]()
Question 37.
Statement 1:
In a combustion reaction in the air, oxygen is the limiting reagent.
Statement 2:
Oxygen is present in limited amount(only 21 %) in air.
(a) Statement (1) is true, Statement (2) is true, Statement (2) is the correct explanation for Statement (1).
(b) Statement (1) is true, Statement (2) is true, Statement (2) is not a correct explanation for Statement (1).
(c) Statement (1) is true, Statement (2) is false.
(d Statement (1) is false, Statement (2) is true.
Answer: (d)
Hint: Correct Statement (1): In a combustion reaction in air, the substance being burnt is the limiting reagent.
Correct Statement (2): Oxygen is present in large excess in the air and is the excess reagent.
Question 38.
Choose the correct Statements from among the following:
In a reaction, A+B2 → 2AB
(a) ‘B’ is the limiting reagent when 300 atoms of A and 200 molecules of B react.
(b) ‘B’ is the limiting reagent when 2 mpl of A and 3 mol of B react.
(c) ‘A’ is the limiting reagent when 100 atoms A and 100 molecules of B react.
(d) ‘A’ is the limiting reagent when 5 mol of ’ A reacts with 2.5 mol of B.
Answer: (a)
Hint: According to given reaction 1 atom of A reacts with one molecule of B. Therefore 200 molecules of B will react with 200 atoms of A and 100 atoms of A will be left unreacted. Hence ‘B’ is the limiting reagent and A is the reagent in excess.
![]()
Question 39.
Choose the correct Statements from among the following:
(a) All atomic masses of atoms are expressed taking C12 isotope as the reference and this scale is referred as unified scale (u).
(b) One atomic mass unit (amu) is equal to the mass of one atom of C – 12 isotope.
(c) The atomic mass of an element is the average relative mass of its atoms (isotopes) as compared to \(\frac{1}{12}\)th mass of the atom of C – 12 isotope.
(d) The empirical formula gives the exact number of atoms of all the elements present in that compound.
Answer: (a)
Hint: Correct Statement:
(b) One atomic mass unit (amu) is equal to \(\frac{1}{12}\)th of the mass of an atom of carbon-12 isotope.
(c) The atomic mass is the average relative masses of atoms compared with an atom of carbon-12 taken as 12.
(d) The empirical formula gives the ratio of the number of different atoms present in a molecule of a compound.
Question 40.
Which of the following Statements about the compound is incorrect?
(a) A molecule of a compound has atoms of different elements.
(b) A compound cannot be separated into its constituents by physical methods of separation.
(c) The compound retains the physical properties of its constituents.
(d) The ratio of atoms of different elements in a compound is fixed.
Answer: (c)
![]()
Question 41.
Sodium sulphate has the formula Na2SO4. Atomic masses of Na, S and oxygen are 23, 32 and 16 respectively. Using these data choose the incorrect Statement among the following.
(a) One mole of sodium sulphate contains two moles of sodium, one mole of sulphur and few moles of oxygen atoms.
(b) One mole of sodium sulphate contains 12.046 × 1023 atoms of sodium.
(c) The mass percentage of sodium, sulphur and oxygen are 45.07, 32.39 and 22.54% respectively.
(d) The molar mass of sodium sulphate is 142 g mol-1.
Answer: (c)
Hint:
Mass % of an element = \(\frac{\left(\begin{array}{c}
\text { mass of that element } \\
\text { in the compound }
\end{array}\right) \times 100}{\text { Molar mass of the compound }}\)
Mass % of Na = \(\frac{46}{142}\) × 100 = 32.39 %
Mass % of S = \(\frac{32}{142}\) × 100 = 22.54 %
Mass % of O = \(\frac{64}{142}\) × 100 = 45.07 %
TN Board 11th Chemistry Important Questions
Must Read: