Students can download Maths Chapter 3 Algebra Ex 3.10 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.10
Question 1.
Solve the following quadratic equations by factorization method
(i) 4x2 – 7x – 2 = 0
Answer:
4x2 – 7x – 2 = 0
4x2 – 8x + x – 2 = 0
4x(x – 2) + 1(x – 2) = 0
(x – 2) + (4x + 1) = 0
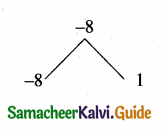
x – 2 = 0 or 4x + 1 = 0 (equate the product of factors to zero)
x = 2 or 4x = -1 ⇒ x = \(\frac { -1 }{ 4 } \)
The roots are 2; \(\frac { -1 }{ 4 } \)
![]()
(ii) 3(p2 – 6) = p(p + 5)
Answer:
3p2 – 18 = p2 + 5p
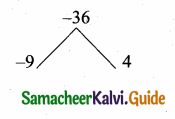
2p2 – 5p – 18 = 0
2p2 – 9p + 4p – 18 = 0
p(2p – 9) + 2(2p – 9) = 0
(2p – 9)(p + 2) = 0
2p – 9 = 0 or p + 2 =
The roots are p = \(\frac { 9 }{ 2 } \), -2
(iii) \(\sqrt{a(a-7)}\) = 3 \(\sqrt{2}\)
Answer:
Squaring on both sides
a(a – 7) = (3\(\sqrt{2}\))2
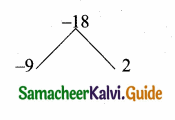
a2 – 7a = 18
a2 – 7a – 18 = 0
(a – 9) (a + 2) = 0
a – 9 = 0 or a + 2 = 0
The roots are -2 and 9
![]()
(iv) \(\sqrt { 2 }\) x2 + 7x + 5\(\sqrt { 2 }\) = 0
Answer:
\(\sqrt { 2 }\) x2 + 7x + 5 \(\sqrt { 2 }\) = 0
\(\sqrt { 2 }\) x2 + 2x + 5x + 5\(\sqrt { 2 }\) = 0
\(\sqrt { 2 }\) x (x + \(\sqrt { 2 }\)) + 5(x + \(\sqrt { 2 }\)) = 0
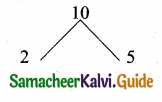
(x + \(\sqrt { 2 }\)) + (\(\sqrt { 2 }\)x + 5) = 0 (equate the product of factors to zero)
x + – \(\sqrt { 2 }\) = 0 or \(\sqrt { 2 }\)x + -5
x = \(\frac{-5}{\sqrt{2}}\)
The roots are – \(\sqrt { 2 }\), \(\frac{-5}{\sqrt{2}}\)
(v) 2x2 – x + \(\frac { 1 }{ 8 } \) = 0
Answer:
2x2 -x + \(\frac { 1 }{ 8 } \) = 0
16x2 – 8x + 1 = (multiply by 8)
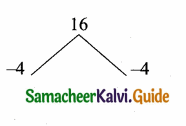
16x2 – 4x – 4x + 1
4x(4x – 1) – 1 (4x – 1) = 0
(4x- 1) (4x- 1) = 0
4x = 1, 4x = 1
x = \(\frac { 1 }{ 4 } \), x = \(\frac { 1 }{ 4 } \)
The roots are \(\frac { 1 }{ 4 } \) and \(\frac { 1 }{ 4 } \)
![]()
Question 2.
The number of volleyball games that must be scheduled in a league with n teams is given by G(n) = \(\frac{n^{2}-n}{2}\) where each team plays with every other team exactly once. A league schedules 15 games. How many teams are in the league?
Solution:
G(n) = \(\frac{n^{2}-n}{2}\)
⇒ 15 = \(\frac{n^{2}-n}{2}\) ⇒ 30 = n2 – n
n2 – n – 30 = 0
⇒ n2 – 6n + 5n – 30 = 0
n(n – 6) + 5 (n – 6) = 0
(n – 6)(n + 5) = 0 ⇒ n = 6, -5
As n cannot be (-ve), n = 6.
∴ There are 6 teams in the league.