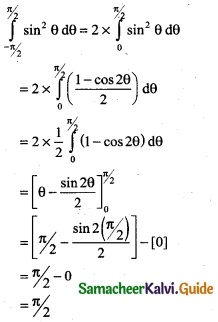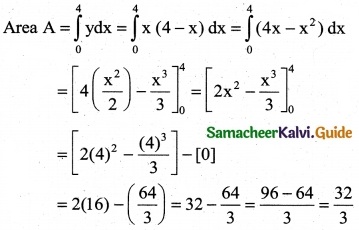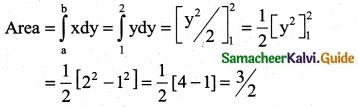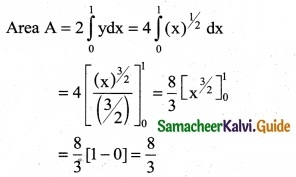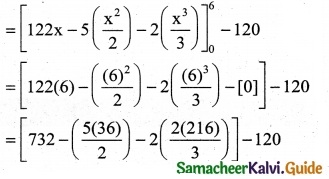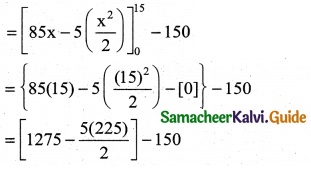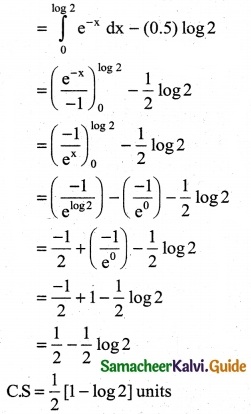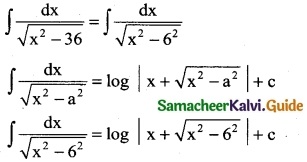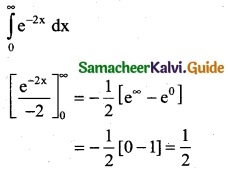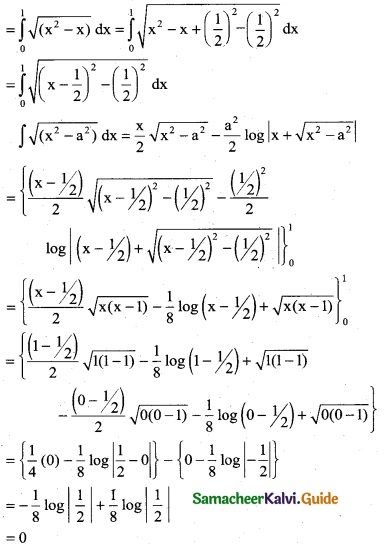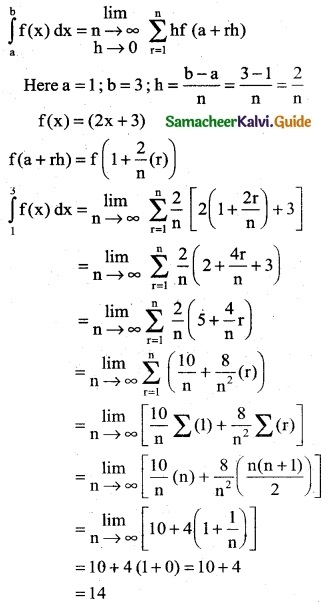Bhagya

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.8 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.8

Using second fundamental theorem, evaluate the following:

Question 1.
\(\int_{0}^{1}\) e^2x dx
Solution:

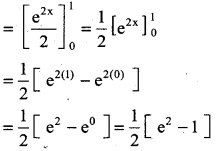
Question 2.
\(\int_{0}^{1/4}\) \(\sqrt { 1 -4x}\) dx
Solution:

Question 3.
\(\int_{0}^{1}\) \(\frac { xdx }{x^2+1}\)
Solution:

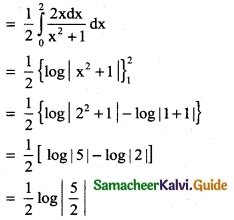
Question 4.
\(\int_{0}^{3}\) \(\frac { e^xdx }{1+e^x}\)
Solution:
\(\int_{0}^{3}\) \(\frac { e^xdx }{1+e^x}\)
= {log |1 + ex|}\(_{0}^{3}\)
= log |1 + e³| – log |1 + e°|
= log |1 + e³| – log |1 + 1|
= log |1 + e³| – log |2|
= log |\(\frac { 1+e^3 }{2}\)|

Question 5.
\(\int_{0}^{1}\) xe^x² dx
Solution:

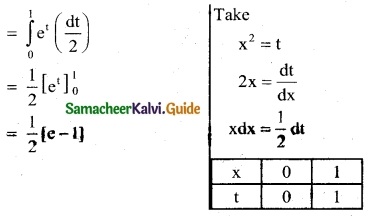
Question 6.
\(\int_{1}^{e}\) \(\frac { dx }{x(1+logx)^3}\)
Solution:

Question 7.
\(\int_{-1}^{1}\) \(\frac { 2x+3 }{x^2+3x+7}\) dx
Solution:

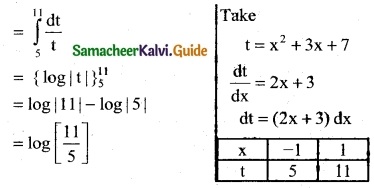
Question 8.
\(\int_{0}^{π/2}\) \(\sqrt { 1 +cosx} \) dx
Solution:

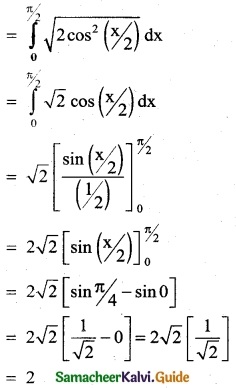
Question 9.
\(\int_{1}^{2}\) \(\frac { x-1 }{x^2}\) dx
Solution:

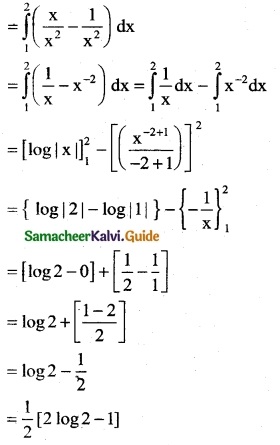
Evaluate the following

Question 10.
\(\int_{1}^{4}\) f(x) dx where f(x) = \(\left\{\begin{array}{l}
4 x+3,1 \leq x \leq 2 \\
3 x+5,2 \end{array}\right.\)
Solution:
\(\int_{1}^{4}\) f(x) dx
= \(\int_{1}^{2}\) f(x) dx + \(\int_{2}^{4}\) f(x) dx
= \(\int_{1}^{2}\) (4x + 3) dx + \(\int_{2}^{4}\) (3x + 5) dx

(8 + 6) – [5] + [24 + 20] – [6 + 10]
= 14 – 5 + 44 – 16
= 58 – 21
= 37

Question 11.
\(\int_{0}^{2}\) f(x) dx where f(x) = \(\left\{\begin{array}{ll}
3-2 x-x^{2}, & x \leq 1 \\
x^{2}+2 x-3, & 1<x \leq 2
\end{array}\right.\)
Solution:
\(\int_{0}^{2}\) f(x) dx
= \(\int_{0}^{1}\) f(x) dx + \(\int_{1}^{2}\) f(x) dx
= \(\int_{0}^{1}\) (3 – 2x – x²) dx + \(\int_{1}^{2}\) (x² + 2x – 3) dx

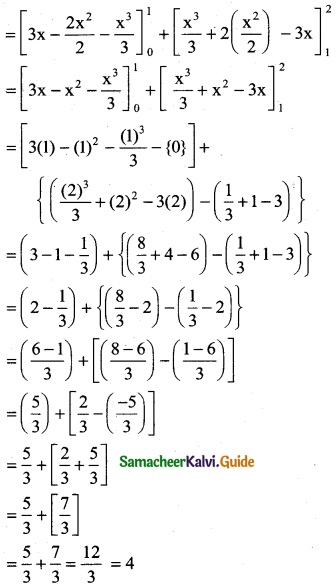
Question 12.
\(\int_{-1}^{1}\) f(x) dx where f(x) = \(\left\{\begin{array}{ll}
x, & x \geq 0 \\
-x, & x<0
\end{array}\right.\)
Solution:
\(\int_{-1}^{1}\) f(x) dx
\(\int_{-1}^{0}\) f(x) dx + \(\int_{0}^{1}\) f(x) dx
= \(\int_{-1}^{0}\) (-x) dx + \(\int_{0}^{1}\) x dx

Question 13.
f(x) = \(\left\{\begin{array}{l}
c x, \quad 0<x<1 \\
0, \text { otherwise }
\end{array}\right.\) find ‘c’ if \(\int_{0}^{1}\) f(x) dx = 2
Solution:
Given
f(x) = \(\left\{\begin{array}{l}
c x, \quad 0<x<1 \\
0, \text { otherwise }
\end{array}\right.\)
⇒ \(\int_{0}^{1}\) f(x) dx = 2
⇒ \(\int_{0}^{1}\) cx dx = 2
c[ \(\frac { x^2 }{ 2 }\) ]\(_{0}^{1}\) = 2
c[ \(\frac { 1 }{ 2 }\) – 0 ] = 2
\(\frac { 1 }{ 2 }\) = 2
⇒ c = 4

Must Read:

MARICO Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.9 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.9

Evaluate the following using properties of definite integrals:

Question 1.
\(\int_{-π/4}^{π/4}\) x³ cos³ x dx
Solution:
Let f(x) = x³cos³x
f(-x) = (-x)³ cos³(-x)
= -x³ cos³x
f(-x) = -f(x)
⇒ f(x) is an odd function
∴ \(\int_{-π/4}^{π/4}\) x³ cos³ x dx = 0

Question 2.
\(\int_{-π/2}^{π/2}\) sin² θ dθ
Solution:
Let f(θ)= sin² θ
f(-θ) = sin² (-θ) = [sin (-θ)]²
= [-sin θ]² = sin² θ
f(-θ) = f(θ)
∴ f(θ) is an even function

Question 3.
\(\int_{-1}^{1}\) log(\(\frac { 2-x }{2+x}\)) dx
Solution:

Question 4.
\(\int_{0}^{π/2}\) \(\frac { sin^7x }{sin^7x+cos^7x}\) dx
Solution:
Using the property
\(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx

Question 5.
\(\int_{0}^{1}\) log (\(\frac { 1 }{x}\) – 1) dx
Solution:

Question 6.
\(\int_{0}^{1}\) \(\frac { x }{(1-x)^{3/4}}\) dx
Solution:
Let I = \(\int_{0}^{1}\) log \(\frac { x }{(1-x)^{3/4}}\) dx
Using the property
\(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx

Read More:

CUB Pivot Point Calculator

Students can download Maths Chapter 3 Bill, Profit and Loss Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

ASTRAL Pivot Point Calculator

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 3 Bill, Profit and Loss Ex 3.2

Miscellaneous Practice Problems

Question 1.
A Shopkeeper buys three articles for Rs 325, Rs 450, and Rs 510. He is able to sell them for Rs 350, Rs 425, and Rs 525 respectively. Find the gain or loss to the shopkeeper on the whole.
Solution:
C.P of three articles = 325 + 450 + 510 = ₹ 1285
S.P of three articles = 350 + 425 + 525 = ₹ 1,300
Here S.P > C.P
Profit = S.P – C.P = 1,300 – 1285 = ₹ 15
The shopkeeper gained = ₹ 15

Question 2.
A stationery shop owner bought a scientific calculator for ₹ 750. He had put a battery worth ₹ 100 in it. He had spent ₹ 50 for its outer pouch. He was able to sell it at ₹ 850. Find his profit or loss.
Solution:
Cost of the scientific calculator = ₹ 750
Cost of its battery = ₹ 100
Cost of outer pouch = ₹ 50
Cost Price of the calculator = ₹ 750 + ₹ 100 + ₹ 50 = ₹ 900
S.P = ₹ 850
Here S.P > C.P
Loss = C.P – S.P = 900 – 850 = ₹ 50
Loss = ₹ 50

Question 3.
Nathan paid Rs 800 and bought 10 bottles of honey from a village vendor. He sold them in a gain for Rs 100 per bottle. Find his profit or loss.
Solution:
C.P of 10 bottles of honey = ₹ 800
C.P of 1 bottle honey = 800/10 = ₹ 80
S.P of a bottle honey = ₹ 100
Here S.P > C.P
Profit per bottle = ₹ 100 – ₹ 80 = ₹ 20
Profit for 10 bottles = 20 × 10 = ₹ 200
Profit = ₹ 200

Question 4.
A man bought 400 metres of cloth for ₹ 60,000 and sold it at the rate of ₹ 400 per metre. Find his profit or loss.
Solution:
C.P of 400 metres of cloth = ₹ 60,000
S.P per metre = ₹ 400
S.P of 400 metres of cloth = 400 × 400 = ₹ 1,60,000
Here S.P > C.P
Profit = C.P – S.P = 1,60,000 – 60,000 = ₹ 1,00,000

Challenge Problems

Question 5.
A fruit seller bought 2 dozen bananas at Rs 20 a dozen and sold them at Rs 3 per banana. Find his gain or loss.
Solution:
Cost of one dozen banana = ₹ 20
Cost of 2 dozen bananas = ₹ 20 × 2 = ₹ 40
C.P = ₹ 40
S.P per banana = ₹ 3
S.P for 2 dozen banana = ₹ 3 × 24 = ₹ 72
Here S.P > C.P
Profit = S.P – C.P = 72 – 40 = 32
Profit = ₹ 32

Question 6.
A store purchased pens at ₹ 216 per dozen. He paid ₹ 58 for conveyance and sold the pens at the discount of n per pen and made an overall profit of ₹ 50. Find the M.P of each pen.
Solution:
Cost of a dozen pens = ₹ 216
Paid for conveyance = ₹ 58
Cost price of 12 pens = 216 + 58 = ₹ 274 [∵ 1 dozen = 12]
Profit of 12 pens = ₹ 50
Profit = S.P – C.P
⇒ 50 = S.P – 274
⇒ S.P = 50 + 274 = ₹ 324
Also discount allowed per pen = ₹ 2
Discount for 12 pens = 2 × 12 = ₹ 24
S.P = M.P – Discount
⇒ 324 = M.P – 24
⇒ M.P = 324 + 24 = ₹ 348
Marked price for 12 pens = ₹ 348
M.P of a pen = \(\frac { 348 }{ 12 }\) = ₹ 29
M.P per pen = ₹ 29

Question 7.
A Vegetable vendor buys 10 kg of tomatoes per day at Rs 10 per kg, for the first three days of a week. 1 kg of tomatoes got smashed every day for those 3 days. For the remaining 4 days of the week, he buys 15 kg of tomatoes daily per kg. If for the entire week he sells tomatoes at Rs 20 per kg, then find his profit or loss for the week.
Solution:
Total tomatoes bought for 3 days = 3 × 10 = 30 kg
Cost of 1 kg = ₹ 10
Cost of 30kg tomatoes = 30 × 10 = ₹ 300
Total tomatoes bought for other 4 days = 4 × 15 = 60 kg
Cost of 1 kg = ₹ 8
Cost of 60 kg tomatoes = 60 × 8 = ₹ 480
Total cost of 90 kg tomatoes = 300 + 480 = ₹ 780
C.P = ₹ 780
Tomatoes smashed = 3 kg
Total kg of Tomatoes for sale = 90 – 3 = 87 kg
S.P of 1 kg tomatoes = ₹ 20
S.P of 87 kg tomatoes = 87 × 20 = ₹ 1740
Here S.P > C.P
Profit = S.P – C.P = 1740 – 780 = ₹ 960
Profit = ₹ 960

Question 8.
An electrician buys a used T.V for ₹ 12,000 and a used Fridge for ₹ 11,000. After spending ₹ 1000 on repairing the T.V and ₹ 1500 on painting the Fridge, he fixes up the M.P of T.V as ₹ 15,000 and that of the Fridge as ₹ 15,500. If he gives each ₹ 1000 discount oh each find his profit or loss.
Solution:
(i) Cost of a T.V = ₹ 12,000
Paid for repair = ₹ 1,000
C.P of the T.V = 12,000 + 1000 = ₹ 13,000
M.P of the T.V = ₹ 15,000
Discount on a TV = ₹ 1000
S.P = M.P – Discount = 15,000 – 1000 = ₹ 14,000
Here S.P > C.P
Profit = S.P – C.P = 14,000 – 13,000 = ₹ 1,000
Profit on the T.V = ₹ 1,000
(ii) Cost of the Fridge = ₹ 11,000
Painting charge = ₹ 1500
C.P of the Fridge = 11000 + 1500 = ₹ 12,500
M.P of the Fridge = ₹ 15,500
Discount allowed = ₹ 1000
S.P = M.P – Discount = ₹ 15,500 – ₹ 1000 = ₹ 14,500
Here also S.P > C.P
Profit = ₹ 14,500 – ₹ 12,500 = ₹ 2000
Total profit = Profit on T.V + Profit on Fridge = ₹ 1000 + ₹ 2000 = ₹ 3000
Profit = ₹ 3000

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.10 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.10

Evaluate the following:

Question 1.
(i) \(\Upsilon\) (4)
Solution:
Γ(4) = Γ(3 + 1) = 3! = 6

(ii) \(\Upsilon\) (\(\frac { 9 }{2}\))
Solution:

(iii) \(\int_{0}^{∞}\) e^-mx x⁶ dx
Solution:
W.K.T \(\int_{0}^{∞}\) xⁿ e^-ax dx = \(\frac { n! }{a^{n+1}}\)
∴ \(\int_{0}^{∞}\) e^-mx x⁶ dx = \(\frac { 6! }{3^{6+1}}\) = \(\frac { 6! }{m^7}\)

(iv) \(\int_{0}^{∞}\) e^-4x x⁴ dx
Solution:

(v) \(\int_{0}^{∞}\) e^-x/2 x⁵ dx
Solution:

Question 2.
If f(x) = \(\left\{\begin{array}{l}
x^{2} e^{-2 x}, x \geq 0 \\
0, \text { otherwise }
\end{array}\right.\), then evaluate \(\int_{0}^{∞}\) f(x) dx
Solution:
Given

Read More:

• ABCAPITAL Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.4

Choose the most suitable answer from the given four alternatives:

Question 1.
Area bounded by the curve y = x (4 – x) between the limits 0 and 4 with x-axis is
(a) \(\frac { 30 }{3}\) sq.unit
(b) \(\frac { 31 }{2}\) sq.unit
(c) \(\frac { 32 }{3}\) sq.unit
(d) \(\frac { 15 }{3}\) sq.unit
Solution:
(c) \(\frac { 32 }{3}\) sq.unit
Hint:

Question 2.
Area bounded by the curve y = e^-2x between the limits 0 < x < ∞ is
(a) 1 sq.units
(b) \(\frac { 1 }{2}\) sq.units
(c) 5 sq.units
(d) 2 sq.units
Solution:
(b) \(\frac { 1 }{2}\) sq.units
Hint:

Question 3.
Area bounded by the curve y = \(\frac { 1 }{x}\) between the limits 1 and 2 is
(a) log 2 sq.units
(b) log 5 sq.units
(c) log 3 sq.units
(d) log 4 sq.units
Solution:
(a) log 2 sq.units
Hint:
Area = \(\int_{1}^{2} \frac{1}{x} d x\)
= \((\log x)_{1}^{2}\)
= log 2 – log 1
= log 2 (Since log 1 = 0)

Question 4.
If the marginal revenue function of a firm is MR = e^{\(\frac { -x }{10}\)} then revenue is
(a) 1 – e^-x/10
(b) e^-x/10 + 10
(c) 10(1 – e^-x/10)
(d) -10e^-x/10
Solution:
(c) 10(1 – e^-x/10)
Hint:
MR = e^{\(\frac { -x }{10}\)} then R = ∫MR dx
R = ∫e^-x/10 dx = \(\frac { e^{-x/10} }{(-1/10)}\) + k
R = -10e^-x/10 + k when x = 0, R = 0
⇒ 0 = -10e⁰ + k
0 = -10(1) + k
∴ k = 10
R = -10e^-x/10 + 10 = 10(1 – e^-x/10)

Question 5.
If MR and MC denotes the marginal revenue and marginal cost functions, then the profit functions is
(a) P = ∫(MR – MC) dx + k
(b) P = ∫(R – C) dx + k
(c) P = ∫(MR + MC)dx + k
(d) P = ∫(MR) (MC) dx + k
Solution:
(a) P = ∫(MR – MC) dx + k
Hint:
Profit = Revenue – Cost

Question 6.
The demand and supply functions are given by D(x) = 16 – x² and S(x) = 2x² + 4 are under perfect competition, then the equilibrium price x is
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
(a) 2
Hint:
D(x) =16 – x² and S(x) = 2x² + 4
Under perfect competition D(x) = S(x)
16 – x² = 2x² + 4; 16 – 4 = 2x² + x²
3x² = 12 ⇒ x² = \(\frac { 12 }{3}\) = 4
∴ x = ± 2, x cannot be in negative
∴ x = 2

Question 7.
The marginal revenue and marginal coast functions of a company are MR = 30 – 6x and MC = -24 + 3x where x is the product, profit function is
(a) 9x² + 54x
(b) 9x² – 54x
(c) 54x – \(\frac { 9x^2 }{2}\)
(d) 54x – \(\frac { 9x^2 }{2}\) + k
Solution:
(d) 54x – \(\frac { 9x^2 }{2}\) + k
Hint:
Profit = ∫(MR – MC) dx + k
= ∫(30 – 60) – (-24 + 3x) dx + k
= ∫(54 – 9x) dx + k
= 54x – \(\frac{9 x^{2}}{2}\) + k

Question 8.
The given demand and supply function are given by D(x) = 20 – 5x and S(x) = 4x + 8 if they are under perfect competition then the equilibrium demand is
(a) 40
(b) \(\frac { 41 }{2}\)
(c) \(\frac { 40 }{3}\)
(d) \(\frac { 41 }{5}\)
Solution:
(c) \(\frac { 40 }{3}\)
Hint:
Under perfect competition D(x) = S(x)
20 – 5x = 4x + 8
20 – 8 = 4x + 5x ⇒ 9x = 12
x = \(\frac { 4 }{3}\)
when x = \(\frac { 4 }{3}\); D(x) = 20 – 5(\(\frac { 4 }{3}\)) = 20 – \(\frac { 20 }{3}\)
= \(\frac { 40 }{3}\)

Question 9.
If the marginal revenue MR = 35 +7x – 3x², then the average revenue AR is.
(a) 35x + \(\frac { 7x^2 }{2}\) – x³
(b) 35x + \(\frac { 7x }{2}\) – x²
(c) 35x + \(\frac { 7x }{2}\) + x²
(d) 35x + 7x + x²
Solution:
(c) \(\frac { 40 }{3}\)
Hint:
R = ∫MR dx = ∫(35 + 7x – 3x²) dx

Question 10.
The profit of a function p(x) is maximum when
(a) MC – MR = 0
(b) MC = 0
(c) MR = 0
(d) MC + MR = 0
Solution:
(a) MC – MR = 0
Hint:
P = Revenue – Cost
P is maximum when \(\frac{d p}{d x}\) = 0
\(\frac{d p}{d x}\) = R'(x) – C'(x) = MR – MC = 0

Question 11.
For the demand function p(x), the elasticity of demand with respect to price is unity then.
(a) revenue is constant
(b) a cost function is constant
(c) profit is constant
(d) none of these
Solution:
(a) Revenue is constant

Question 12.
The demand function for the marginal function MR = 100 – 9x² is
(a) 100 – 3x²
(b) 100x – 3x²
(c) 100x – 9x²
(d) 100 + 9x²
Solution:
(a) 100 – 3x²
Hint:
R = ∫(MR) dx + c₁
R = ∫(100 – 9x²) dx + c₁
R = 100x – 3x³ + c₁
When R = 0, x = 0, c₁ = 0
R = 100x – 3x³
Demand function is \(\frac{R}{x}\) = 100 – 3x²

Question 13.
When x₀ = 5 and p₀ = 3 the consumer’s surplus for the demand function p_d = 28 – x²
(a) 250 units
(b) \(\frac { 250 }{3}\) units
(c) \(\frac { 251 }{2}\) units
(d) \(\frac { 251 }{3}\) units
Solution:
(b) \(\frac { 250 }{3}\) units
Hint:

Question 14.
When x₀ = 2 and P₀ = 12 the producer’s surplus for the supply function P₀ = 2x² + 4 is
(a) \(\frac { 31 }{5}\) units
(b) \(\frac { 31 }{2}\) units
(c) \(\frac { 32 }{2}\) units
(d) \(\frac { 30 }{7}\) units
Solution:
(c) \(\frac { 32 }{2}\) units
Hint:
Producer’s Surplus

Question 15.
Area bounded by y = x between the lines y = 1, y = 2 with y = axis is
(a) \(\frac { 1 }{2}\) sq units
(b) \(\frac { 5 }{2}\) sq units
(c) \(\frac { 3 }{2}\) sq units
(d) 1 sq units
Solution:
(c) \(\frac { 3 }{2}\) sq units
Hint:

Question 16.
The producer’s surplus when supply the function for a commodity is p = 3 + x and x₀ = 3 is
(a) \(\frac { 1 }{2}\)
(b) \(\frac { 9 }{2}\)
(c) \(\frac { 3 }{2}\)
(d) \(\frac { 7 }{2}\)
Solution:
(b) \(\frac { 9 }{2}\)
Hint:
p = 3 + x and x₀ = 3
then p₀ = 3 + 3 = 6

Question 17.
The marginal cost function is MC = 100√x find AC given that TC = 0 when the out put is zero is
(a) \(\frac { 200 }{3}\) x^1/2
(b) \(\frac { 200 }{3}\) x^3/2
(c) \(\frac { 200 }{3x^{3/2}}\)
(d) \(\frac { 200 }{3x^{1/2}}\)
Solution:
(a) \(\frac { 200 }{3}\) x^1/2
Hint:
TC = ∫MC dx = ∫100√x dx = 100 ∫(x)^1/2 dx

Question 18.
The demand and supply function of a commodity are P(x) = (x – 5)² and S(x) = x² + x + 3 then the equilibrium quantity x₀ is
(a) 5
(b) 2
(c) 3
(d) 10
Solution:
(b) 2
Hint:
At equilibrium, P(x) = S(x)
⇒ (x – 5)² = x² + x + 3
⇒ x² – 10x + 25 = x² + x + 3
⇒ 11x = 22
⇒ x = 2

Question 19.
The demand and supply function of a commodity are D(x) = 25 – 2x and S(x) = \(\frac { 10+x }{2}\) then the equilibrium price P₀ is
(a) 2
(b) 2
(c) 3
(d) 10
Solution:
(a) 2
Hint:
At equilibrium, D(x) = S(x)
25 – 2x = \(\frac{10+x}{4}\)
⇒ 100 – 8x = 10 + x
⇒ x = 10
That is x₀ = 10
P₀ = 25 – 2(x₀) = 25 – 20 = 5

Question 20.
If MR and MC denote the marginal revenue and marginal cost and MR – MC = 36x – 3x² – 81, then maximum profit at x equal to
(a) 3
(b) 6
(c) 9
(d) 10
Solution
(c) 9
Hint:
Profit P = ∫(MR – MC) dx = ∫(36x – 3x² – 81) dx
P = [\(\frac { 36x^2 }{2}\) – \(\frac { 3x^3 }{3}\) – 81x] = 18x² – x³ – 81x
when p = 0; 18x² – x³ – 81x = 0 ⇒ x² – 18x + 81 = 0
(x – 9)² = 0 ⇒ x – 9 = 0
∴ x = 9

Question 21.
If the marginal revenue of a firm is constant, then the demand function is
(a) MR
(b) MC
(c) C(x)
(d) AC
Solution:
(a) MR
Hint:
MR = k (constant)
Revenue function R = ∫(MR) dx + c₁
= ∫kdx + c₁
= kx + c₁
When R = 0, x = 0, ⇒ c₁ = 0
R = kx
Demand function p = \(\frac{R}{x}=\frac{k x}{x}\) = k constant
⇒ p = MR

Question 22.
For a demand function p, if ∫\(\frac { dp }{p}\) = k ∫\(\frac { dx }{x}\) then k is equal to
(a) n_d
(b) -n_d
(c) \(\frac { -1 }{n_d}\)
(d) \(\frac { 1 }{n_d}\)
Solution:
(c) \(\frac { -1 }{n_d}\)

Question 23.
The area bounded by y = e^x between the limits 0 to 1 is
(a) (e – 1) sq.units
(b) (e + 1) sq.units
(c) (1 – \(\frac { 1 }{e}\)) sq.units
(d) (1 + \(\frac { 1 }{e}\)) sq.units
Solution:
(a) (e – 1) sq.units
Hint:
Area A = \(\int_{a}^{b}\)ydx = \(\int_{0}^{1}\)e^xdx = [e^x]\(_{0}^{1}\)
= [e^x – e°] = [e – 1]

Question 24.
The area bounded by the parabola y² = 4x bounded by its latus rectum is
(a) \(\frac { 16 }{3}\) sq units
(b) \(\frac { 8 }{3}\) sq units
(c) \(\frac { 72 }{3}\) sq units
(d) \(\frac { 1 }{3}\) sq units
Solution:
(b) \(\frac { 8 }{3}\) sq units
Hint:

y² = 4x ⇒ y = \(\sqrt { 4x}\) 2√x = 2(x)^1/2
In this parabola 4a = 4 ⇒ a = 1 and vertex V(0, 0)

Question 25.
The area bounded by y = |x| between the limits 0 and 2 is
(a) 1 sq.units
(b) 3 sq.units
(c) 2 sq.units
(d) 4 sq.units
Solution:
(c) 2 sq.units
Hint:
Area A = \(\int_{a}^{b}\)ydx = \(\int_{0}^{2}\)x dx = [ \(\frac { x^2 }{2}\) ]\(_{0}^{2}\)
= \(\frac { (2)^2 }{2}\) – (0) = \(\frac { 4 }{2}\) = 2

Must Read:

Icici Bank Pivot Point

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.3

Question 1.
Calculate consumer’s surplus if the demand function p = 50 – 2x and x = 20
Solution:
Demand function p = 50 – 2x and x = 20
when x = 20, p = 50 – 2(20)
p = 50 – 40 = 10
∴ p₀ = 10
CS = \(\int _{0}^{x}\) (demand function) dx – (Price × quantity demanded)
= \(\int _{0}^{20}\) (50 – 2x)dx – (10 × 20)
= [50x – 2(\(\frac { x^2 }{2}\))]\( _{0}^{20}\) – 200
= [50x – x²]\( _{0}^{20}\) – 200
= {50(20) – (20)² – [0]} – 200
= (1000 – 400) – 200
= 600 – 200
∴ C.S = 400 units

Question 2.
Calculate consumer’s surplus if the demand function p = 122 – 5x – 2x² and x = 6.
Solution:
Demand function p = 122 – 5x – 2x² and x = 6
when x = 6; p = 122 – 5(6) – 2(6)²
= 122 – 30 – 2 (36)
= 122 – 102 = 20
∴ p₀ = 20
C.S = \(\int _{0}^{x}\) (demand function) dx – (Price × quantity demanded)
= \(\int _{0}^{6}\)(122 – 5x – 2x²) dx – (20 × 6)

[732 – 5(18) – 2(72)] – 120
= 732 – 90 – 144 – 120
= 732 – 354 = 378
∴ CS = 378 units

Question 3.
The demand function p = 85 – 5x and supply function p = 3x – 3. Calculate the equilibrium price and quantity demanded. Also calculate consumer’s surplus.
Solution:
Demand function p = 85 – 5x
Supply function p = 3x – 35
W.K.T. at equilibrium prices p_d = p_s
85 – 5x = 3x – 35
85 + 35 = 3x + 5x
120 = 8x ⇒ x = \(\frac { 120 }{8}\)
∴ x = 15
when x = 15 p₀ = 85 – 5(15) = 85 – 75 = 10
C.S = \(\int _{0}^{x}\) f(x) dx – x₀p₀
= \(\int _{0}^{x}\) (85 – 5x) dx – (15)(10)

= 1275 – \(\frac { 1125 }{2}\) – 150
= 1275 – 562.50 – 150
= 1275 – 712.50
∴ CS = 562.50 units

Question 4.
The demand function for a commodity is p = e^-x. Find the consumer’s surplus when p = 0.5
Solution:
The demand function p = e^-x
when p = 0.5 ⇒ 0.5 = e^-x
\(\frac { 1 }{2}\) = \(\frac { 1 }{e^x}\) ⇒ e^x = 2
∴ x = log 2
∴ Consumer’s surplus
C.S = \(\int _{0}^{x}\) (demand function) dx – (Price × quantity demanded)

Question 5.
Calculate the producer’s surplus at x = 5 for the supply function p = 7 + x
Solution:
The supply function p = 7 + x
when x = 5 ⇒ p = 7 + 5 = 12
∴ x₀ = 5 and p₀ = 12
Producer’s surplus

Question 6.
If the supply function for a product is p = 3x + 5x². Find the producer’s surplus when x = 4
Solution:
The supply function p = 3x + 5x²
when x = 4 ⇒ p = 3(4) + 5(4)²
p = 12 + 5(16)= 12 + 80
p = 92
∴ x₀ = 4 and p₀ = 92
Producer’s Surplus

Question 7.
The demand function for a commodity is p = \(\frac { 36 }{x+4}\) Find the producer’s surplus when the prevailing market price is Rs 6.
Solution:
The demand function for a commodity
p = \(\frac { 36 }{x+4}\)
when p = 6 ⇒ 6 = \(\frac { 36 }{x+4}\)
x + 4 = \(\frac { 36 }{6}\) ⇒ x + 4 = 6
x = 2
∴ p₀ = 6 and x₀ = 2
The consumer’s surplus
C.S = \(\int _{0}^{x}\) f(x) dx – x₀p₀
= \(\int _{0}^{2}\) (\(\frac { 36 }{x+4}\)) dx – 2(6)
= 36 [log (x + 4)]\(_{0}^{2}\) – 12
= 36 [log (2 + 4) – log (0 + 4)] – 12
= 36 [log6 – log4] – 12
= 36[log(\(\frac { 6 }{4}\))] – 12
∴ CS = 36 log(\(\frac { 6 }{4}\)) – 12 units

Question 8.
The demand and supply functions under perfect competition are pd = 1600 – x² and p_s = 2x² + 400 respectively, find the producer’s surplus.
Solution:
pd = 1600 – x² and p_s = 2x² + 400
Under the perfect competition p_d = p_s
1600 – x² = 2x² + 400
1600 – 400 = 2x² + x² ⇒ 1200 = 3x²
⇒ x² – 400 ⇒ x = 20 or -20
The value of x cannot be negative, x = 20 when x₀ = 20;
p₀ = 1600 – (20)² = 1600 – 400
P₀ = 1200
PS = x₀p₀ – \(\int _{0}^{x_0}\) g(x) dx

Question 9.
Under perfect competition for a commodity the demand and supply laws are P_d = \(\frac { 8 }{x+1}\) – 2 and Ps = \(\frac { x+3 }{2}\) respectively. Find the consumer’s and producer’s surplus.
Solution:

16 – (x² + 3x + x + 3) = 2 [2(x + 1)]
16 – (x² + 4x + 3) = 4(x + 1)
16 – x² – 4x – 3 = 4x + 4
x² + 4x + 4x + 4 + 3 – 16 = 0
x² + 8x – 9 = 0
(x + 9) (x – 1) = 0 ⇒ x = -9 (or) x = 1
The value of x cannot be negative x = 1 when x₀ = 1
p₀ = \(\frac { 8 }{1+1}\) – 2 ⇒ p₀ = \(\frac { 8 }{2}\) – 2
p₀ = 4 – 2 ⇒ p₀ = 2
CS = \(\int _{0}^{x}\) f(x) dx – x₀p₀
= \(\int _{0}^{1}\) (\(\frac { 8 }{x+1}\) – 2) dx – (1) (2)
= {8[log(x + 1)] – 2x}\(\int _{0}^{1}\) – 2
= 8 {[log (1 + 1) – 2(1)] – 8 [log (0 + 1) – 2(0)]} – 2
= [8 log (2) – 2 – 8 log1] – 2
= 8 log(\(\frac { 8 }{2}\)) – 2 – 2
C.S = (8 log 2 – 4) units
P.S = x₀p₀ – \(\int _{0}^{x_0}\) g(x) dx

Question 10.
The demand equation for a products is x = \(\sqrt {100-p}\) and the supply equation is x = \(\frac {p}{2}\) – 10. Determine the consumer’s surplus and producer’s, under market equilibrium.
Solution:
p_d = \(\sqrt {100-p}\) and p_s = \(\sqrt {100-p}\)
Under market equilibrium, p_d = p_s
\(\sqrt {100-p}\) = \(\frac {p}{2}\) – 10
Squaring on both sides

36p = p² ⇒ p² – 36 p = 0
p (p – 36) = 0 ⇒ p = 0 or p = 36
The value of p cannot be zero, ∴p₀ = 36 when p₀ = 36
x₀ = \(\sqrt {100-36}\) = \(\sqrt {64}\)
∴ x₀ = 8

= 288 – [x² + 20x]\( _{0}^{8}\)
= 288 – { [(8)² + 20(8)] – [0]}
= 288 – [64 + 160]
= 288 – 224 = 64
PS = 64 Units

Question 11.
Find the consumer’s surplus and producer’s surplus for the demand function pd = 25 – 3x and supply function ps = 5 + 2x
Solution:
p_d = 25 – 3x and p_s = 5 + 2x
Under market equilibrium, p_d = p_s
25 – 3x = 5 + 2x
25 – 5 = 2x + 3x ⇒ 5x = 20
∴ x = 4
when x = 4
P₀ = 25 – 3(4)
= 25 – 12 = 13
p₀ = 13

= 52 – [5x + x²]\( _{0}^{4}\)
= 52 – (5(4) + (4)²) – (0)}
= 52 – [20 + 16]
= 52 – 36
∴ PS = 16 units

Try More:

What Is Nr7 Candle

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.2

Question 1.
The cost of an overhaul of an engine is Rs 10,000 The Operating cost per hour is at the rate of 2x-240 where the engine has run x km. find out the total cost of the engine run for 300 hours after overhaul.
Solution:
Given that the overhaul cost is Rs. 10,000.
The marginal cost is 2x – 240
MC = 2x – 240
C = ∫ MC dx + k
C = x² – 240x + k
k is the overhaul cost
⇒ k = 10,000
So C = x² – 240x + 10,000
When x = 300 hours, total cost is
C = (300)² – 240(300) + 10,000
⇒ C = 90,000 – 72000 + 10,000
⇒ C = 28,000
So the total cost of the engine run for 300 hours after the overhaul is ₹ 28,000.

Question 2.
Elasticity of a function \(\frac { Ey }{Ex}\) is given by \(\frac { Ey }{Ex}\) = \(\frac { -7x }{(1-2x)(2+3x)}\). Find the function when x = 2, y = \(\frac { 3 }{8}\)
Solution:

Put x = 0
7 = A (3(0) + 2) + B (2(0) – 1)
7 = A (2) + B (-1)
7 = (2) (2) – B
B = 4 – 7
B = -3

Question 3.
The Elasticity of demand with respect to price for a commodity is given by where \(\frac { (4-x)}{x}\) p is the price when demand is x. find the demand function when the price is 4 and the demand is 2. Also, find the revenue function
Solution:
The elasticity at the demand

Integrating on both sides
∫\(\frac { 1}{(x-4)}\) = ∫\(\frac { 1}{p}\) dp
log |x – 4| = log |p| + log k
log |x – 4| = log |pk| ⇒ (x – 4) = pk ……… (1)
when p = 4 and x = 2
(2 – 4) = 4k ⇒ -2 = 4k
k = -1/2
Eqn (1) ⇒ (x – 4) = p(-1/2)
-2 (x – 4) = p ⇒ p = 8 – 2x
Revenue function R = px = (8 – 2x)x
R = 8x – 2x²

Question 4.
A company receives a shipment of 500 scooters every 30 days. From experience it is known that the inventory on hand is related to the number of days x. Since the shipment, I (x) = 500 – 0.03 x², the daily holding cost per scooter is Rs 0.3. Determine the total cost for maintaining inventory for 30 days
Solution:
Here I (x) = 500 – 0.03 x²
C¹ = Rs 0.3
T = 30
Total inventory carrying cost
= C¹ \(\int _{0}^{T}\) I(x) dx
= 0.3 \(\int _{0}^{30}\) (500 – 0.03 x²)dx
= 0.3 [500 x – 0.03(\(\frac { x^3 }{3}\))]\( _{0}^{30}\)
= 0.3 [ 500 x – 0.01 x³]\( _{0}^{30}\)
= 0.3 [500(30) – 0.01 (30)³] – [0]
= 0.3 [15000 – 0.01 (27000)]
= 0.3 [15000 – 270] = 0.3 [14730]
= Rs 4,419

Question 5.
An account fetches interest at the rate of 5% per annum compounded continuously an individual deposits Rs 1000 each year in his account. how much will be in the account after 5 years (e^0.25 = 1.284)
Solution:
P = 1000
r = \(\frac { 5 }{1000}\) = 0.05
N = 5
Annuity = \(\int _{0}^{5}\) 1000 e^0.05t dt
= 1000 [ \(\frac { e^{0.05t} }{0.05}\) ] \(_{0}^{5}\)
= \(\frac { 1000 }{0.05}\) [e^0.05(5) – e⁰]
= 20000 [e^0.25 – 1]
= 20000 [1.284 – 1]
= 20000 [0.284]
= Rs 5680

Question 6.
The marginal cost function of a product is given by \(\frac { dc }{dx}\) = 100 – 10x + 0.1 x² where x is the output. Obtain the total and average cost function of the firm under the assumption, that its fixed cost is t 500
Solution:
\(\frac { dc }{dx}\) = 100 – 10x + 0.1 x² and k = Rs 500
dc = (100 – 10x + 0.1 x²) dx
Integrating on both sides,

Question 7.
The marginal cost function is M.C = 300 x^2/5 and the fixed cost is zero. Find the total cost as a function of x
Solution:
M.C = 300 x^2/5 and fixed cost K = 0
Total cos t = ∫M.C dx

Question 8.
If the marginal cost function of x units of output is \(\frac { a }{\sqrt {ax+b}}\) and if the cost of output is zero. Find the total cost as a function of x.
Solution:

∴ C(x) = 2(ax + b)^1/2 + k …….. (1)
When x = 0
eqn (1) ⇒ 0 = 2 [a(0) + b]^1/2 + k
k = -2(b)^1/2 ⇒ k = -2√b
Required cost function
C(x) = 2(ax + b)^1/2 – 2√b
∴ C = 2\(\sqrt { ax + b}\) – 2√b

Question 9.
Determine the cost of producing 200 air conditioners if the marginal cost (is per unit) is C'(x) = \(\frac { x^2 }{200}\) + 4
Solution:

= 13333.33 + 800
∴ Cost of producing 200 air conditioners
= Rs 14133.33

Question 10.
The marginal revenue (in thousands of Rupees) function for a particular commodity is 5 + 3 e^-0.03x where x denotes the number of units sold. Determine the total revenue from the sale of 100 units (given e^-3 = approximately)
Solution:
The marginal Revenue (in thousands of Rupees) function
M.R = 5 + 3^-0.03x
Total Revenue from sale of 100 units is
Total Revenue T.R = \(\int _{0}^{ 100}\) M.R dx

= [500 – 100 e^-3] – [0 – 100 e°]
= [500 -100 (0.05)] – [-100 (1)]
= [500 – 5]+ 100
= 495 + 100 = 595 thousands
= 595 × 1000
∴ Revenue R = Rs 595000

Question 11.
If the marginal revenue function for a commodity is MR = 9 – 4x². Find the demand function.
Solution:
Marginal Revenue function MR = 9 – 4x²
Revenue function R = ∫MR dx

Question 12.
Given marginal revenue function \(\frac { 4 }{(2x+3)^2}\) -1, show that the average revenue function is P = \(\frac { 4 }{6x+9}\) -1
Solution:
M.R = \(\frac { 4 }{(2x+3)^2}\) -1
Total Revenue R = ∫M.R dx

Question 13.
A firms marginal revenue functions is M.R = 20 e^-x/10 Find the corresponding demand function.
Solution:

Question 14.
The marginal cost of production of a firm is given by C’ (x) = 5 + 0.13 x, the marginal revenue is given by R’ (x) = 18 and the fixed cost is Rs 120. Find the profit function.
Solution:
MC = C'(x) = 5 + 0.13x
C(x) = ∫C'(x) dx + k₁
= ∫(5 + 0.13x) dx + k₁
= 5x + \(\frac{0.13}{2} x^{2}\) + k₁
When quantity produced is zero, fixed cost is 120
(i.e) When x = 0, C = 120 ⇒ k₁ = 120
Cost function is 5x + 0.065x² + 120
Now given MR = R'(x) = 18
R(x) = ∫18 dx + k₂ = 18x + k₂
When x = 0, R = 0 ⇒ k₂ = 0
Revenue = 18x
Profit P = Total Revenue – Total cost = 18x – (5x + 0.065x² + 120)
Profit function = 13x – 0.065x² – 120

Question 15.
If the marginal revenue function is R'(x) = 1500 – 4x – 3x². Find the revenue function and average revenue function.
Solution:
Given marginal revenue function
MR = R’(x)= 1500 – 4x – 3x²
Revenue function R(x) = ∫R'(x) dx + c
R = ∫(1500 – 4x – 3x²) dx + c
R = 1500x – 2x² – x³ + c
When x = 0, R = 0 ⇒ c = 0
So R = 1500x – 2x² – x³
Average revenue function P = \(\frac{R}{x}\) ⇒ 1500 – 2x – x²

Question 16.
Find the revenue function and the demand function if the marginal revenue for x units MR = 10 + 3x – x
Solution:
The marginal revenue function
MR = 10 + 3x – x²
The Revenue function
R = ∫(MR) dx
= ∫(10 + 3x – x²)dx

Question 17.
The marginal cost function of a commodity is given by M_c = \(\frac { 14000 }{\sqrt{7x+4}}\) and the fixed cost is Rs 18,000. Find the total cost average cost.
Solution:
The marginal cost function of a commodity
M_c = \(\frac { 14000 }{\sqrt{7x+4}}\) = 14000 (7x + 4)^-1/2
Fixed cost k = Rs 18,000
Total cost function C = ∫(M.C) dx
= ∫14000 (7x + 4)^-1/2 dx

Question 18.
If the marginal cost (MC) of production of the company is directly proportional to the number of units (x) produced, then find the total cost function, when the fixed cost is Rs 5,000 and the cost of producing 50 units is Rs 5,625.
Solution:
M.C αx
M.C = λx
fixed cost k = Rs 5000
Cost function C = ∫(M.C) dx
= ∫λx dx

Question 19.
If MR = 20 – 5x + 3x², Find total revenue function
Solution:
MR = 20 – 5x + 3x²
Total Revenue function
R = ∫(MR) dx = ∫(20 – 5x + 3x²) dx
R = 20x – \(\frac { 5x^2 }{2}\) + \(\frac {3x^3 }{3}\) + k
when x = 0; R = 0 ⇒ k = 0
∴ R = 20x – \(\frac { 5 }{2}\) x² + x³

Question 20.
If MR = 14 – 6x + 9x², Find the demand function.
Solution:
MR = 14 – 6x + 9x²
R = ∫(14 – 6x + 9x²) dx + k
= 14x – 3x² + 3x³ + k
Since R = 0, when x = 0, k = 0
So revenue function R = 14x – 3x² + 3x³
Demand function P = \(\frac{R}{x}\) = 14 – 3x + 3x²

Must Try:

Nifty Resistance Support Levels Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.12 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.12

Choose the most suitable answer from the given four alternatives:

Question 1.
∫\(\frac { 1 }{x^3}\) dx is
(a) \(\frac { -3 }{x^2}\) + c
(b) \(\frac { -1 }{2x^2}\) + c
(c) \(\frac { -1 }{3x^2}\) + c
(d) \(\frac { -2 }{x^2}\) + c
Solution:
(b) \(\frac { -1 }{2x^2}\) + c
Hint:
∫\(\frac { 1 }{x^3}\) dx = ∫x^-3 dx = [ \(\frac { x^{-3+1} }{-3+1}\) ] + c
= (\(\frac { x^{-2} }{-2}\)) + c = \(\frac { -1 }{2x^2}\) + c

Question 2.
∫2^x dx is
(a) 2^x log 2 + c
(b) 2^x + c
(c) \(\frac { 2^x }{log 2}\) + c
(d) \(\frac { log 2 }{2^x}\) + c
Solution:
(c) \(\frac { 2^x }{log 2}\) + c
Hint:
∫2^x dx = ∫a^x dx = \(\frac { a^x }{log a}\) + c

Question 3.
∫\(\frac { sin 2x }{2 sin x}\) dx is
(a) sin x + c
(b) \(\frac { 1 }{2}\) sin x + c
(c) cos x + c
(d) \(\frac { 1 }{2}\) cos x + c
Solution:
(a) sin x + c
Hint:
∫\(\frac { sin 2x }{2 sin x}\) dx = ∫\(\frac { 2sin x cos x }{2 sin x}\) dx
= ∫cos x dx
= sin x + c

Question 4.
∫\(\frac { sin 5x-sin x }{cos 3x}\) dx is
(a) -cos 2x + c
(b) -cos 2x – c
(c) –\(\frac { 1 }{4}\) cos 2x + c
(d) -4 cos 2x + c
Solution:
(a) -cos 2x + c
Hint:

Question 5.
∫\(\frac { log x}{x}\) dx, x > 0 is
(a) \(\frac { 1 }{2}\) (log x)² + c
(b) –\(\frac { 1 }{2}\) (log x)²
(c) \(\frac { 2 }{x^2}\) + c
(d) \(\frac { 2 }{x^2}\) – c
Solution:
(a) \(\frac { 1 }{2}\) (log x)² + c
Hint:
∫\(\frac { log x}{x}\) dx, x > 0
∫ tdt = [ \(\frac { t^2 }{2}\) ] + c
= \(\frac { (log x)^2 }{2}\) + c
let t = log x
\(\frac { dt }{dx}\) = \(\frac { 1 }{x}\)
dt = \(\frac { 1 }{x}\) dx

Question 6.
∫\(\frac { e^x }{\sqrt{1+e^x}}\) dx is
(a) \(\frac { e^x }{\sqrt{1+e^x}}\) + c
(b) 2\(\sqrt{1+e^x}\) + c
(c) \(\sqrt{1+e^x}\) + c
(d) e^x\(\sqrt{1+e^x}\) + c
Solution:
(b) 2\(\sqrt{1+e^x}\) + c
Hint:

Question 7.
∫\(\sqrt { e^x}\) dx is
(a) \(\sqrt { e^x}\) + c
(b) 2\(\sqrt { e^x}\) + c
(c) \(\frac { 1 }{2}\) \(\sqrt { e^x}\) + c
(d) \(\frac { 1 }{2\sqrt { e^x}}\) + c
Solution:
(b) 2\(\sqrt { e^x}\) + c
Hint:
∫\(\sqrt { e^x}\) dx
= ∫\(\sqrt { e^x}\) dx = ∫(e^x)^1/2 dx = ∫ e^x/2 dx
= \(\frac { e^{x/2} }{1/2}\) + c = 2e^x/2 + c
= 2(e^x)^1/2 + c = 2\(\sqrt { e^x}\) + c

Question 8.
∫e^2x [2x² + 2x] dx
(a) e^2x x² + c
(b) xe^2x + c
(c) 2x²e² + c
(d) \(\frac { x^2e^x }{2}\) + c
Solution:
(a) e^2x x² + c
Hint:
∫e^2x (2x² + 2x) dx
Let f(x) = x²; f'(x) = 2x and a = 2
= ∫e^ax [af(x),+ f ’(x)] = e^ax f(x) + c
= ∫e^2x (2x² + 2x) dx = e^2x (x²) + c

Question 9.
\(\frac { e^x }{e^x+1}\) dx is
(a) log |\(\frac { e^x }{e^x+1}\)| + c
(b) log |\(\frac { e^x+1 }{e^x}\)| + c
(c) log |e^x| + c
(d) log |e^x + 1| + c
Solution:
(d) log |e^x + 1| + c
Hint:
∫\(\frac { e^x }{e^x+1}\) dx
= ∫\(\frac { dt }{t}\)
= log |t| + c
= log |e^x + 1| + c
take t = e^x + 1
\(\frac { dt }{dx}\) = e^x
dt = e^x dx

Question 10.
∫\(\frac { 9 }{x-3}-\frac { 1 }{x+1}\) dx is
(a) log |x – 3| – log|x + 1| + c
(b) log|x – 3| + log|x + 1| + c
(c) 9 log |x – 3| – log |x + 1| + c
(d) 9 log |x – 3| + log |x + 1| + c
Solution:
(c) 9 log |x – 3| – log |x + 1| + c
Hint:

Question 11.
∫\(\frac { 2x^3 }{4+x^4}\) dx is
(a) log |4 + x⁴| + c
(b) \(\frac { 1 }{2}\) log |4 + x⁴| + c
(c) \(\frac { 1 }{2}\) log |4 + x⁴| + c
(d) log |\(\frac { 2x^3 }{4+x^4}\) + c
Solution:
(b) \(\frac { 1 }{2}\) log |4 + x⁴| + c
Hint:

Question 12.
∫\(\frac { dx }{\sqrt{x^2-36}}\) is
(a) \(\sqrt{x^2-36}\) + c
(b) log |x + \(\sqrt{x^2-36}\)| + c
(c) log |x – \(\sqrt{x^2-36}\)| + c
(d) log |x² + \(\sqrt{x^2-36}\)| + c
Solution:
(b) log |x + \(\sqrt{x^2-36}\)| + c
Hint:

Question 13.
∫\(\frac { 2x+3 }{\sqrt{x^2+3x+2}}\) dx is
(a) \(\sqrt{x^2+3x+2}\) + c
(b) 2\(\sqrt{x^2+3x+2}\) + c
(c) \(\sqrt{x^2+3x+2}\) + c
(d) \(\frac { 2 }{3}\) (x² + 3x + 2) + c
Solution:
(b) 2\(\sqrt{x^2+3x+2}\) + c
Hint:

Question 14.
\(\int_{0}^{4}\) (2x + 1) dx is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2
Hint:
\(\int_{0}^{4}\) (2x + 1) dx
= [2(\(\frac { x^2 }{2}\)) + x]\(_{0}^{1}\) = [x² + x]\(_{0}^{1}\)
= [(1)² + (1)] – [0] = 2

Question 15.
\(\int_{2}^{4}\) \(\frac { dx }{x}\) is
(a) log 4
(b) 0
(c) log 2
(d) log 8
Solution:
(c) log 2
Hint:
\(\int_{2}^{4}\) \(\frac { dx }{x}\)
\(\int_{2}^{4}\) \(\frac { dx }{x}\) = [log |x|]\(_{0}^{1}\) = log |4| – log |2|
= log[ \(\frac { 4}{2}\) ] = log 2

Question 16.
\(\int_{0}^{∞}\) e^-2x dx is
(a) 0
(b) 1
(c) 2
(d) \(\frac { 1 }{2}\)
Solution:
(d) \(\frac { 1 }{2}\)
Hint:

Question 17.
\(\int_{-1}^{1}\) x³ e^x4 dx is
(a) 1
(b) 2\(\int_{0}^{1}\) x³ e^x4
(c) 0
(d) e^x4
Solution:
(c) 0
Hint:
\(\int_{-1}^{1}\) x³ e^x4 dx
Let f (x) = x³e^x4
f(-x) = (-x)² e^(-x)4
= -x² e^x4
f(-x) = -f(x)
⇒ f(x) is an odd function
∴ \(\int_{-1}^{1}\) x³ e^x4 dx = 0

Question 18.
If f(x) is a continuous function and a < c < b, then \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\) f(x) dx is
(a) \(\int_{a}^{b}\) f(x) dx – \(\int_{a}^{c}\) f(x) dx
(b) \(\int_{a}^{c}\) f(x) dx – \(\int_{a}^{b}\) f(x) dx
(c) \(\int_{a}^{b}\) f(x) dx
(d) 0
Solution:
(c) \(\int_{a}^{b}\) f(x) dx

Question 19.
The value of \(\int_{-π/2}^{π/2}\) cos x dx is
(a) 0
(b) 2
(c) 1
(d) 4
Solution:
(b) 2
Hint:
\(\int_{-π/2}^{π/2}\) cos x dx
Let f(x) = cos x
f(-x) = cos (-x) = cos (x) = f(x)
∴ f(x) is an even function
\(\int_{-π/2}^{π/2}\) cos x dx = 2 × \(\int_{0}^{π/2}\) cos x dx
= 2 × [sin x]\(_{0}^{-π/2}\) = 2 [sin π/2 – sin 0]
= 2 [1 – 0] = 2

Question 20.
\(\int_{-π/2}^{π/2}\) \(\sqrt {x^4(1-x)^2}\) dx
(a) \(\frac { 1 }{12}\)
(b) \(\frac { -7 }{12}\)
(c) \(\frac { 7 }{12}\)
(d) \(\frac { -1 }{12}\)
Solution:
(a) \(\frac { 1 }{12}\)
Hint:

Question 21.
If \(\int_{0}^{1}\) f(x) dx = 1, \(\int_{0}^{1}\) x f(x) dx = a and \(\int_{0}^{1}\) x² f(x) dx = a², then \(\int_{0}^{1}\) (a – x)² f(x) dx is
(a) 4a²
(b) 0
(c) a²
(d) 1
Solution:
(b) 0
Hint:
\(\int_{0}^{1}\) (a – x)² f(x) dx
= \(\int_{0}^{1}\) [a² +x² – 2ax] f(x) dx
= \(\int_{0}^{1}\) a² + f (x) dx + \(\int_{0}^{1}\) x² f (x) dx – 2a\(\int_{0}^{1}\) x f(x) dx
= a²(1) + a² – 2a(a) – 2a² – 2a² = 0

Question 22.
The value of \(\int_{2}^{3}\) f(5 – x) dx – \(\int_{2}^{3}\) f(x) dx is
(a) 1
(b) 0
(c) -1
(d) 5
Solution:
(b) 0
Hint:
\(\int_{2}^{3}\) f(5 – x) dx – \(\int_{2}^{3}\) f(x) dx
Using the property
= \(\int_{2}^{3}\) f(x) dx = \(\int_{a}^{b}\) f(a + b – x) dx
= \(\int_{2}^{3}\) f (5 – x) – \(\int_{2}^{3}\) f (5 – x) dx
= 0

Question 23.
\(\int_{0}^{4}\) (√x + \(\frac { 1 }{√x}\)), dx is
(a) \(\frac { 20 }{3}\)
(b) \(\frac { 21 }{3}\)
(c) \(\frac { 28 }{3}\)
(d) \(\frac { 1 }{3}\)
Solution:
(c) \(\frac { 28 }{3}\)
Hint:

Question 24.
\(\int_{0}^{π/3}\) tan x dx is
(a) log 2
(b) 0
(c) log √2
(d) 2 log 2
Solution:
(a) log 2
Hint:
\(\int_{0}^{π/3}\) tan x dx
= ∫tan x dx
= ∫\(\frac { sin x }{cos x}\) dx
= -∫\(\frac { -sin x }{cos x}\) dx
= -log |cos x| + c
= log sec x + c
= [log (sec x)]\(_{0}^{π/3}\)
= log [(sec π/3) – log (sec 0)]
= log (2) – log (1)
= log 2 – (0) = log 2

Question 25.
Using the factorial representation of the gamma function, which of the following is the solution for the gamma function Γ(n) when n = 8
(a) 5040
(b) 5400
(c) 4500
(d) 5540
Solution:
(a) 5040
Hint:
\(\Upsilon\) (8) = 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

Question 26.
Γ(n) is
(a) (n – 1)!
(b) n!
(c) n Γ (n)
(d) (n – 1) Γ(n)
Solution:
(a) (n – 1)!
Hint:
Γ(n) = Γ(n – 1) + 1 = (n – 1)!

Question 27.
Γ(1) is
(a) 0
(b) 1
(c) n
(d) n!
Solution:
(b) 1
Hint:
\(\Upsilon\) (1) = 0! = 1

Question 28.
If n > 0, then Γ(n) is
(a) \(\int_{0}^{1}\) e^-x x^n-1 dx
(b) \(\int_{0}^{1}\) e^-x xⁿ dx
(c) \(\int_{0}^{∞}\) e^x x^-n dx
(d) \(\int_{0}^{∞}\) e^-x x^n-1 dx
Solution:
(d) \(\int_{0}^{∞}\) e^-x x^n-1 dx

Question 29.
Γ(\(\frac { 3 }{2}\))
(a) √π
(b) \(\frac { √π }{2}\)
(c) 2√π
(d) \(\frac { 3 }{2}\)
Solution:
(b) \(\frac { √π }{2}\)
Hint:
\(\Upsilon\) (3/2) = \(\frac { 2 }{2}\) \(\Upsilon\) [ \(\frac { 3 }{2}\) ]
= \(\frac { 3 }{2}\) √π

Question 30.
\(\int_{0}^{∞}\) x⁴ e^-x dx is
(a) 12
(b) 4
(c) 4!
(d) 64
Solution:
(b) \(\frac { √π }{2}\)
Hint:
\(\int_{0}^{∞}\) x⁴ e^-x dx
= ∫xⁿ e^-ax dx = \(\frac { n! }{a{n+1}}\)
= \(\frac { 4! }{(1)^{n+1}}\)
= \(\frac { 4! }{(1)^5}\)
= 4!

Must Read:

Gann Square Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Miscellaneous Problems

Question 1.
∫\(\frac { 1 }{\sqrt{x-1}-\sqrt{x+3}}\) dx
Solution:
∫\(\frac { 1 }{\sqrt{x+2}-\sqrt{x+3}}\) dx
Conjugating the Denominator

Question 2.
∫\(\frac { dx }{2-3x-2x^2}\)
Solution:

Question 3.
∫\(\frac { dx }{e^x+6+5e^{-x}}\)
Solution:

Question 4.
∫\(\sqrt { 2x^2-3}\) dx
Solution:

Question 5.
∫\(\sqrt { 9x^2+12x+3}\) dx
Solution:

Question 6.
∫(x + 1)² log x dx
Solution:
∫udv = uv – ∫vdu
∫(x + 1)² log x dx

Question 7.
∫log (x – \(\sqrt { x^2-1}\)) dx
Solution:

Question 8.
\(\int_{0}^{1}\) \(\sqrt { x(x-1)}\) dx
Solution:

Question 9.
\(\int_{-1}^{1}\) x² e^-2x dx
Solution:

Question 10.
\(\int_{0}^{3}\) \(\frac { xdx }{\sqrt {x+1} + \sqrt{5x+1}}\)
Solution:

Try More:

MARICO Pivot Point Calculator

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.11 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.11

Evaluate the following integrals as the limit of the sum:

Question 1.
\(\int_{0}^{1}\) (x + 4) dx
Solution:

Question 2.
\(\int_{1}^{3}\) x dx
Solution:

Question 3.
\(\int_{1}^{3}\) (2x + 3) dx
Solution:

Question 4.
\(\int_{0}^{1}\) x² dx
Solution:

Try More:

MANAPPURAM Pivot Point Calculator