Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.2
Question 1.
Find the GCD of the given polynomials by Division Algorithm
(i) x4 + 3x3 – x – 3, x3 + x2 – 5x + 3
Answer:
p(x) = x4 + 3x3 – x – 3
g(x) = x3 + x2 – 5x + 3
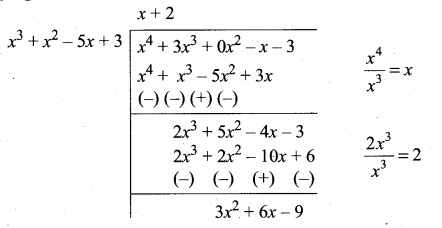
3x2 + 6x – 9 = 3(x2 + 2x – 3)
Now dividing g(x) = x3 + x2 – 5x + 3
by the new remainder
(leaving the constant 3)
we get x2 + 2x – 3
G.C.F. = x2 + 2x – 3

![]()
(ii) x4 – 1, x3 – 11x2 + x – 11
p(x) = x4 – 1
g(x) = x3 – 11x2 + x – 11
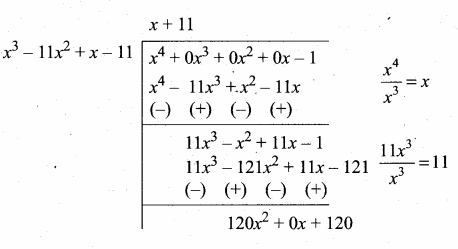
120x2 + 120 = 120 (x2 + 1)
Now dividing g(x) = x3 – 11x2 + x – 11 by the new remainder (leaving the constant) we get x2 + 1
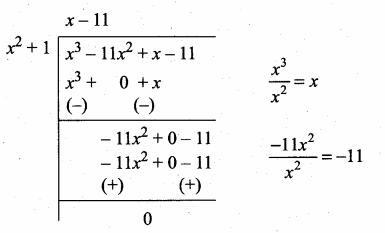
G.C.D. = x2 + 1
(iii) 3x4 + 6x3 – 12x2 – 24x, 4x4 + 14x3 + 8x2 – 8x
Answer:
p(x) = 3x4 + 6x3 – 12x2 – 24x
= 3x (x3 + 2x2 – 4x – 8)
g(x) = 4x4 + 14x3 + 8x2 – 8x
= 2x (2x3 + 7x2 + 4x – 4)
G.C.D. of 3x and 2x = x
Now g(x) is divide by p(x) we get
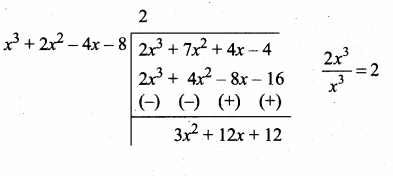
![]()
3x2 + 12x + 12 = 3 (x2 + 4x + 4)
Now dividing p(x) = x3 + 2x2 – 4x – 8
by the new remainder
(leaving the constant)
x2 + 4x + 4
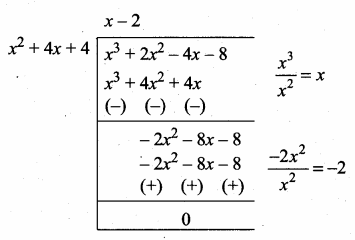
G.C.D. = x(x2 + 4x + 4) [Note x is common for p(x) and g(x)]
(iv) 3x3 + 3x2 + 3x + 3, 6x3 + 12x2 + 6x+12
p(x) = 3x3 + 3x2 + 3x + 3
= 3(x3 + x2 + x + 1)
g(x) = 6x3 + 12x2 + 6x + 12
= 6(x3 + 2x2 + x + 2)
G.C.D. of 3 and 6 = 3
Now g(x) is divided by p(x)
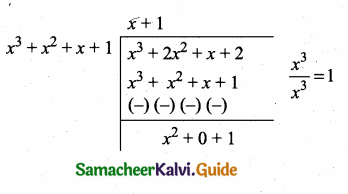
Now dividing p(x) by the remainder x2 + 1
we get x + 1
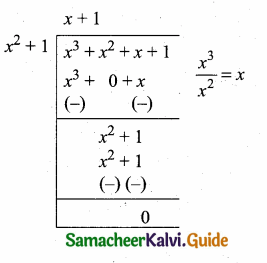
∴ G.C.D. = 3(x2 + 1) [3 is the G.C.D. of 3 and 6]
![]()
Question 2.
Find the LCM of the given polynomials
(i) 4x2y, 8x3y2
Answer:
4x2 y = 2 × 2 × x2 × y
8 x3 y2 = 2 × 2 × 2 × x3 × y2
L.C.M. = 23 × x3 × y2
= 8x3y2
Aliter: L.C.M of 4 and 8 = 8
L.C.M. of x2y and x3y2 = x3y2
∴ L.C.M. = 8x3y2
(ii) -9a3b2, 12a2b2c
Answer:
-9a3b2 = -(32 × a3 × b2)
12a2b2c = 22 × 3 × a2 × b2 × c
L.C.M. = -(22 × 32 × a3 × b2 × c)
= -36 a3b2c
![]()
(iii) 16m, -12m2n2, 8n2
Answer:
16m = 24 × m
-12 m2n2 = -(22 × 3 × m2 × n2)
8n2 = 23 × n2
L.C.M. = -(24 × 3 × m2 × n2)
= -48 m2n2
(iv) p2 – 3p + 2, p2 – 4
Answer:
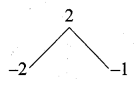
P2 – 3p + 2 = p2 – 2p – p + 2
= p(p – 2) – 1 (p – 2)
= (p – 2) (p – 1)
p2 – 4 = p2 – 22 (using a2 – b2 = (a + b) (a – b)]
= (p + 2) (p – 2)
L.C.M. = (p – 2) (p + 2) (p – 1)
![]()
(v) 2x2 – 5x – 3,4.x2 – 36
Answer:
2x2 – 5x – 3 = 2x2 – 6x + x – 3
= 2x (x – 3) + 1 (x – 3)
= (x – 3) (2x + 1)
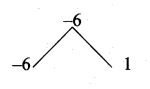
= 4x2 – 36 = 4 [x2 – 9]
= 4 [x2 – 32]
= 4(x + 3) (x – 3)
L.C.M. = 4(x – 3) (x + 3) (2x + 1)
![]()
(vi) (2x2 – 3xy)2,(4x – 6y)3,(8x3 – 27y3)
Answer:
(2x2 – 3xy)2 = x2 (2x – 3y)2
(4x – 6y)3 = 23 (2x – 3y)3
= 8 (2x – 3y)3
8x3 – 27y3 = (2x)3 – (3y)3
= (2x – 3y) [(2x)2 + 2x × 3y + (3y2)]
[using a3 – b3 = (a – b) (a2 + ab + b2)
(2x – 3y) (4x2 + 6xy + 9y2)
L.C.M. = 8x2 (2x – 3y)3 (4x2 + 6xy + 9y)2