Samacheer Kalvi 10th Maths Guide Chapter 5 Coordinate Geometry Ex 5.1

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.1

Question 1.
Find the area of the triangle formed by the points
(i) (1,-1), (-4, 6) and (-3, -5)
(ii) (-10, -4), (-8, -1) and (-3, -5)
Solution:
(i) Let the vertices A (1, -1), B (-4, 6) and C (-3, -5)


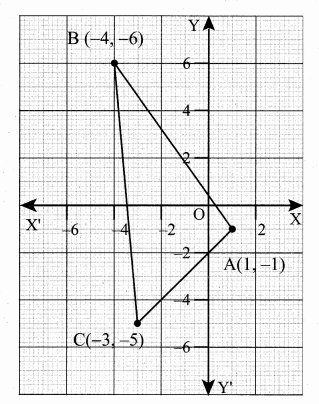
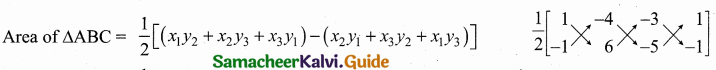
= \(\frac { 1 }{ 2 } \) [(6 + 20 + 3) – (4 – 18 – 5)] = \(\frac { 1 }{ 2 } \) [29 – (-19)] = \(\frac { 1 }{ 2 } \) [29 + 19]
= \(\frac { 1 }{ 2 } \) × 48 = 24 sq. units.
Area of ∆ABC = 24 sq. units

(ii) Let the vertices be A(-10, -4), B(-8 -1) and C(-3, -5)

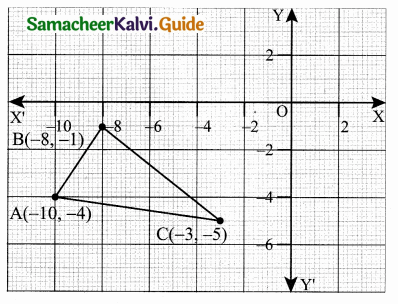
Area of ∆ABC = \(\frac { 1 }{ 2 } \)[(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]
= \(\frac { 1 }{ 2 } \) [(50 + 3 + 32) – (12 + 40 + 10)]

= \(\frac { 1 }{ 2 } \) [85 – (62)] = \(\frac { 1 }{ 2 } \) [23] = 11.5
Area of ∆ACB = 11.5 sq.units

Question 2.
Determine whether the sets of points are collinear?
(i) (-\(\frac { 1 }{ 2 } \),3)
(ii) (a,b + c), (b,c + a) and (c,a + b)
Solution:
(i) Let the points be A (-\(\frac { 1 }{ 2 } \),3), B (-5, 6) and C(-8, 8)
Area of ∆ABC = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₃ + x₁y₃)]
= \(\frac { 1 }{ 2 } \) [(- 3 – 40 – 24) – (-15 – 48 – 4)]

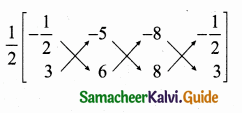
= \(\frac { 1 }{ 2 } \) [-67 + 67] = \(\frac { 1 }{ 2 } \) × 0 = 0
Area of a ∆ is 0.
∴ The three points are collinear.

(ii) Let the points be A (a, b + c), B (b, c + a) and C (c, a + b)
Area of the triangle = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]

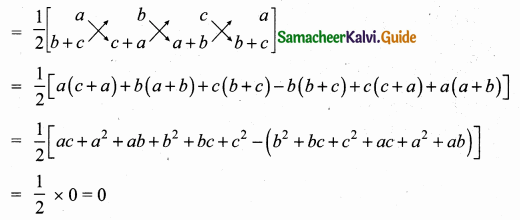
Since the area of a triangle is 0.
∴ The given points are collinear.

Question 3.
Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’

Solution:
(i) Let the vertices be A (0,0) B (p, 8), c (6, 2)
Area of a triangle = 20 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 20

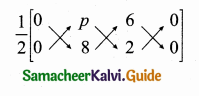
\(\frac { 1 }{ 2 } \) [(0 + 2p + 0) – (0 + 48 + 0)] = 20
\(\frac { 1 }{ 2 } \) [2p – 48] = 20
2p – 48 = 40 ⇒ 2p = 40 + 48
p = \(\frac { 88 }{ 2 } \) = 44
The value of p = 44

(ii) Let the vertices be A (p, p), B (5, 6) and C (5, -2)
Area of a triangle = 32 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 32

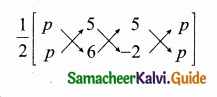
\(\frac { 1 }{ 2 } \) [6p – 10 + 5p) – (5p + 30 – 2p)] = 32
\(\frac { 1 }{ 2 } \) [11 p – 10 – 3p – 30] = 32
11p – 10 – 3p – 30 = 64
8p – 40 = 64
8p = 64 + 40 ⇒ 8p = 104
p = \(\frac { 104 }{ 8 } \) = 13
The value of p = 13

Question 4.
In each of the following, find the value of ‘a’ for which the given points are collinear.
(i) (2,3), (4, a) and (6, -3)
(ii) (a, 2 – 2a), (-a + 1, 2a) and (-4 -a, 6 – 2a).
Solution:
(i) Let the points be A (2, 3), B(4, a) and C(6, -3).
Since the given points are collinear.
Area of a triangle = 0
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 0)

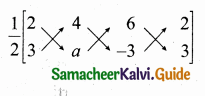
\(\frac { 1 }{ 2 } \) [(2a – 12 + 18) – (12 + 6a – 6)] = 0
2a + 6 – (6 + 6a) = 0
2a + 6 – 6 – 6a = 0
-4a = 0 ⇒ a = \(\frac { 0 }{ 4 } \) = 0
The value of a = 0

(ii) Let the points be A (a, 2 – 2a), B (-a + 1, 2a) C (-4 -a, 6 – 2a).
Since the given points are collinear.
Area of a ∆ = 0

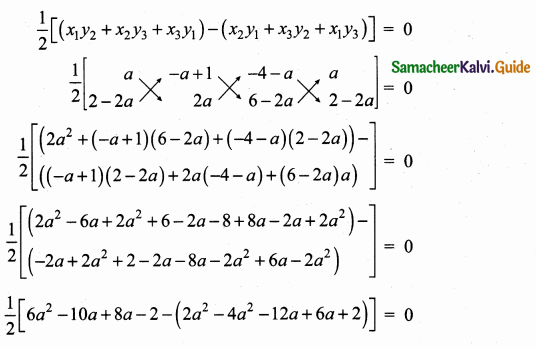
6a² – 2a – 2 – (-2a² – 6a + 2) = 0
6a² – 2a – 2 + 2a² + 6a – 2 = 0
8a² + 4a – 4 = 0 (Divided by 4)
2a² + a – 1 = 0
2a² + 2a – a – 1 = 0
2a (a + 1) – 1 (a + 1) = 0

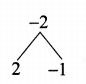
(a + 1) (2a – 1) = 0
a + 1 = 0 (or) 2a – 1 = 0
a = -1 (or) 2a = 1 ⇒ a = \(\frac { 1 }{ 2 } \)
The value of a = -1 (or) \(\frac { 1 }{ 2 } \)

Question 5.
Find the area of the quadrilateral whose vertices are at
(i) (-9, -2), (-8, -4), (2, 2) and (1, -3)
(ii) (-9, 0), (-8,6), (-1, -2) and (-6, -3)
Solution:
(i) Let the vertices A (-9, -2), B(-8, -4), C(2, 2) and D(1, -3).
Plot the vertices in a graph.

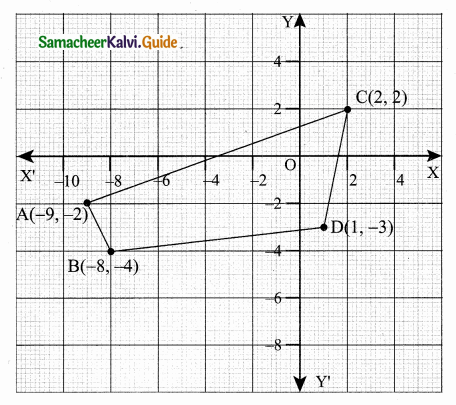
[Note: Consider the points in counter clock wise order]

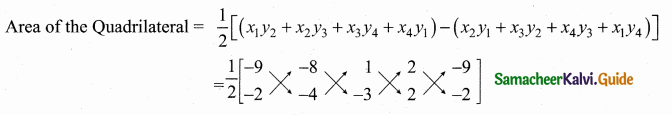
Area of the Quadrilateral ABDC = \(\frac { 1 }{ 2 } \) [36 + 24 + 2 – 4 – (16 – 4 – 6 – 18)]
= \(\frac { 1 }{ 2 } \) [58 – (-12)] – \(\frac { 1 }{ 2 } \)[58 + 12]
= \(\frac { 1 }{ 2 } \) × 70 = 35 sq. units 2
Area of the Quadrilateral = 35 sq. units

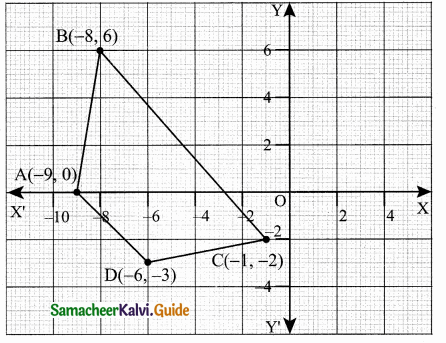
(ii) Let the vertices A(-9, 0), B(-8, 6), C(-1, -2) and D(-6, -3)
Plot the vertices in a graph and take them in counter – clock wise order.
Area of the Quadrilateral DCB

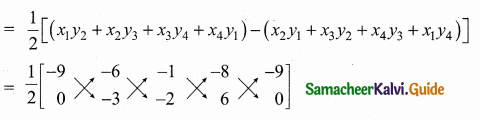
= \(\frac { 1 }{ 2 } \) [33 + 35] = \(\frac { 1 }{ 2 } \) × 68 = 34 sq. units
Area of the Quadrilateral = 34 sq. units

Question 6.
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (-4, -2), (-3, k), (3, -2) and (2, 3)
Solution:
Let the vertices A (-A, -2), B (-3, k), C (3, -2) and D (2, 3)
Area of the Quadrilateral = 28 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)] = 28

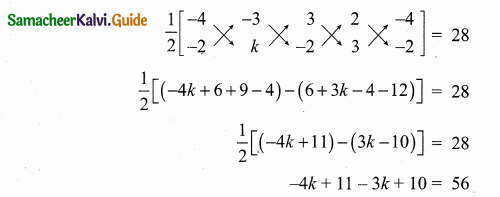
-7k + 21 = 56
-7k = 56 – 21
-7k = 35 ⇒ 7k = – 35
k = – \(\frac { 35 }{ 7 } \) = -5
The value of k = -5

Question 7.
If the points A(-3, 9), B(a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.
Solution:
Since the three points are collinear
Area of a ∆ = 0

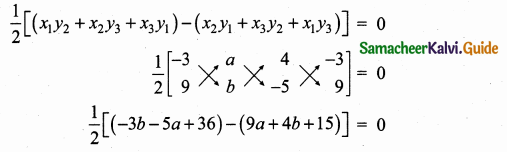
-3b – 5a + 36 – 9a – 4b – 15 = 0
-7b – 14a + 21 = 0
(÷ by 7) – b – 2a + 3 = 0
2a + b – 3 = 0

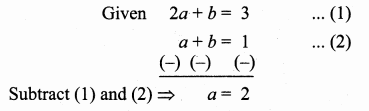
Substitute the value of a = 2 in (2) ⇒ 2 + b = 1
b = 1 – 2 = -1
The value of a = 2 and b = -1

Question 8.
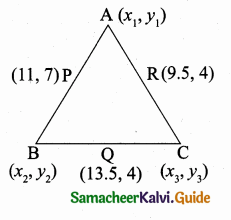
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC . Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Solution:
Let the vertices of the ∆ABC be A(x₁,y₁), B(x₂,y₂), C(x₃,y₃)

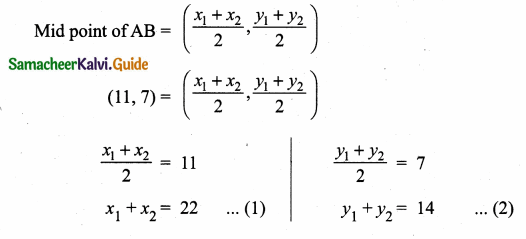
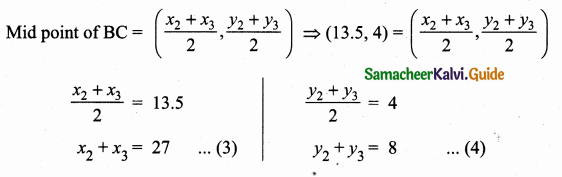
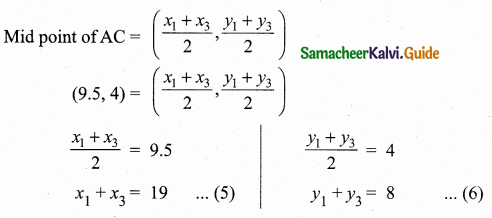
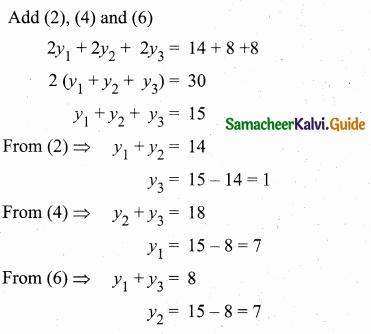
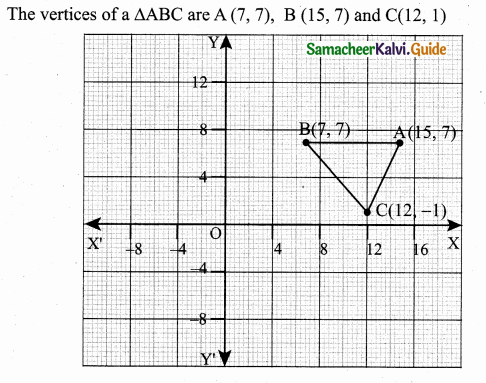
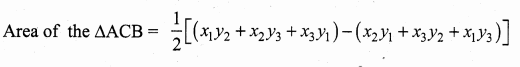
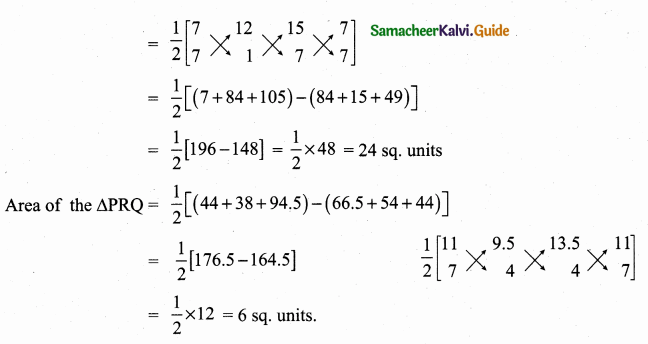
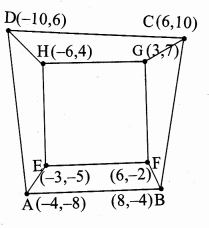
Question 9.
In the figure, the quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio.

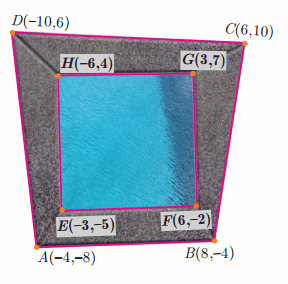
Solution:

= \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)]
= \(\frac { 1 }{ 2 } \) [(16 + 80 + 36 + 80) – (-64 – 24 – 100 – 24)]
= \(\frac { 1 }{ 2 } \) [212 – (-212)]

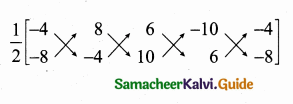
= \(\frac { 1 }{ 2 } \) [212 + 212] = \(\frac { 1 }{ 2 } \) [424] = 212 sq. units

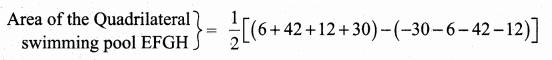
= \(\frac { 1 }{ 2 } \) [90 – (-90)]

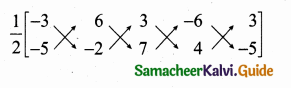
= \(\frac { 1 }{ 2 } \) [90 + 90]
= \(\frac { 1 }{ 2 } \) × 180 = 90 sq. units
Area of the patio = Area of the Quadrilateral ABCD – Area of the Quadrilateral EFGH
= (212 – 90) sq. units
Area of the patio = 122 sq. units

Question 10.
A triangular shaped glass with vertices at A(-5, -4), B(l, 6) and C(7, -4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied.
Solution:
Given the vertices of the triangular glass is A (-5, -4), B (1, 6), and C (7, -4)


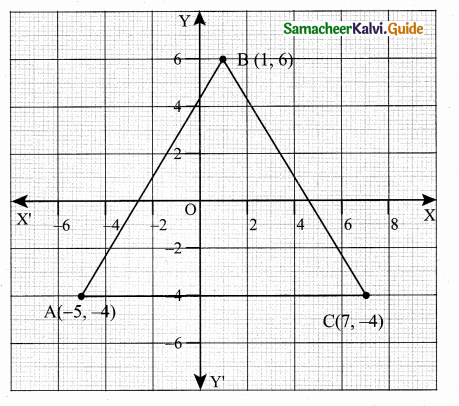
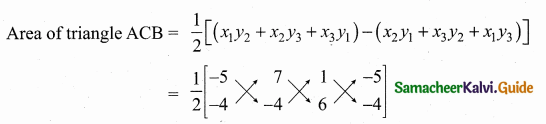
= \(\frac { 1 }{ 2 } \) [(20 + 42 – 4) – (-28 – 4 – 30)]
= \(\frac { 1 }{ 2 } \) [58 – (-62)]
= \(\frac { 1 }{ 2 } \) [58 + 62]
= \(\frac { 1 }{ 2 } \) × 120 = 60 sq. feet
Number of cans to paint 6 square feet = 1
∴ Number of cans = \(\frac { 60 }{ 6 } \) = 10 ⇒ Number of cans = 10

Question 11.
In the figure, find the area of
(i) triangle AGF
(ii) triangle FED
(iii) quadrilateral BCEG.

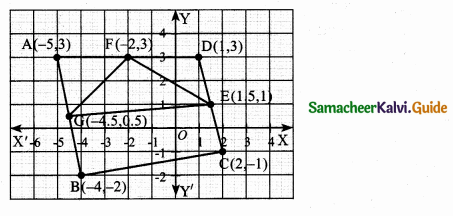
Solution:
Area of a triangle = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]
(i) Area of ∆AGF = \(\frac { 1 }{ 2 } \) [(-2.5 – 13.5 – 6) – (-13.5 – 1 – 15)]
= \(\frac { 1 }{ 2 } \) [-22 – (-29.5)]

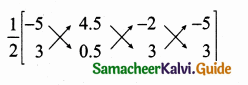
= \(\frac { 1 }{ 2 } \) [-22 + 29.5]
= \(\frac { 1 }{ 2 } \) × 7.5 = 3.75 sq.units

(ii) Area of ∆FED = \(\frac { 1 }{ 2 } \) [(-2 + 4.5 + 3) – (4.5 + 1 – 6)]
= \(\frac { 1 }{ 2 } \) [5.5 – (-0.5)]

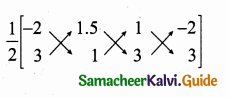
= \(\frac { 1 }{ 2 } \) [5.5 + 0.5] = \(\frac { 1 }{ 2 } \) × 6 = 3 sq.units

(iii)

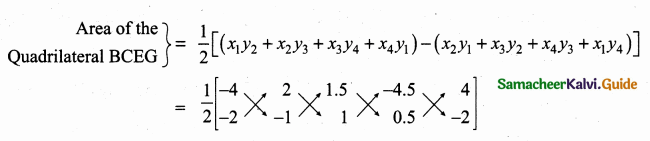
= \(\frac { 1 }{ 2 } \) [(4 + 2 + 0.75 + 9) – (-4 -1.5 – 4.5 -2)]
= \(\frac { 1 }{ 2 } \) [15.75 + 12]
= \(\frac { 1 }{ 2 } \) [27.75] = 13.875
= 13.88 sq. units