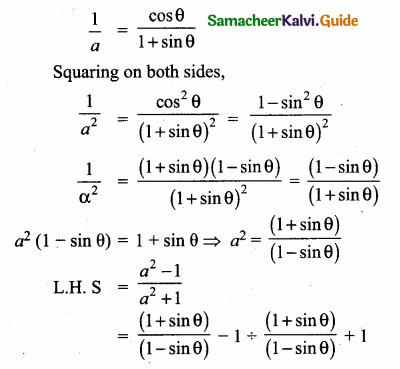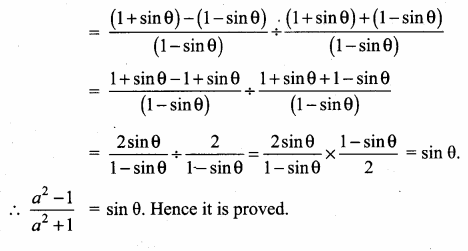Samacheer Kalvi 10th Maths Guide Chapter 6 Trigonometry Ex 6.1

Students can download Maths Chapter 6 Trigonometry Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.1

Question 1.
Prove the following identities.
(i) cot θ + tan θ = sec θ cosec θ
(ii) tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
Answer:
(i) L. H. S = cot θ + tan θ
= \(\frac{\cos \theta}{\sin \theta}+\frac{\sin \theta}{\cos \theta}\)
= \(\frac{\cos ^{2} \theta+\sin ^{2} \theta}{\sin \theta \cos \theta}\)
[cos² θ + sin² θ = 1]
= \(\frac{1}{\sin \theta \cos \theta}\)
= sec θ . cosec θ = R. H. S
∴ cot θ + tan θ = sec θ cosec θ

(ii) tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
L.H.S = tan⁴ θ + tan² θ
= tan² θ (tan² θ + 1)
= tan² θ sec² θ
R.H.S = sec⁴ θ – sec² θ
= sec² θ (sec² θ – 1)
= sec² θ tan² θ
L.H.S = R.H.S
∴ tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

Question 2.
Prove the following identities.
(i) \(\frac{1-\tan ^{2} \theta}{\cot ^{2} \theta-1}\) = tan² θ
(ii) \(\frac{\cos \theta}{1+\sin \theta}\) = sec θ – tan θ
Answer:
(i) \(\frac{1-\tan ^{2} \theta}{\cot ^{2} \theta-1}\) = tan² θ

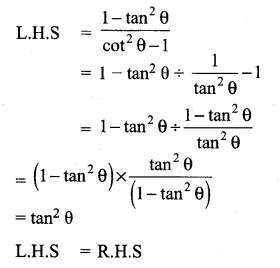
(ii) \(\frac{\cos \theta}{1+\sin \theta}\) = sec θ – tan θ

Aliter:
L.H.S = \(\frac{\cos \theta}{1-\sin \theta}\)
[conjugate (1 – sin θ)]

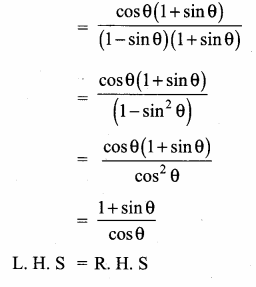
Question 3.
Prove the following identities.

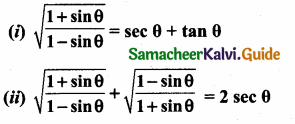
Solution:

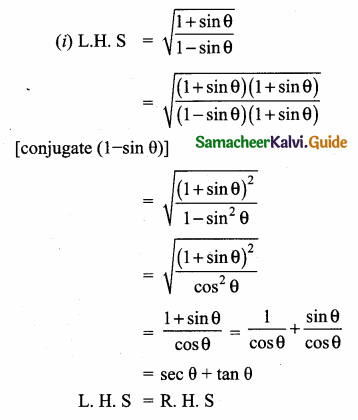
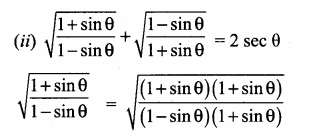
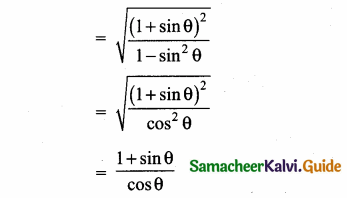
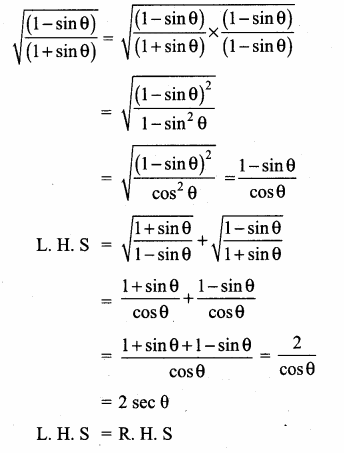
Question 4.
Prove the following identities.
(i) sec⁶ θ = tan⁶ θ + 3 tan² θ sec² θ + 1
(ii) (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²
Answer:
(i) sec⁶ θ = tan⁶ θ + 3 tan² θ sec² θ + 1
L.H.S = sec⁶ θ
= (sec² θ)³ = (1 + tan² θ)³
= 1 + (tan² θ)³ + 3 (1) (tan² θ) (1 + tan² θ) [(a + b)³ = a³ + b³ + 3 ab (a + b)]
= 1 + tan⁶ θ + 3 tan² θ(1 + tan² θ)
= 1 + tan⁶ θ + 3 tan² θ (sec² θ)
= 1 + tan⁶ θ + 3 tan² θ sec² θ
= tan⁶ θ + 3 tan² θ sec² θ + 1
L.H.S = R.H.S

(ii) (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²
L.H.S = (sin θ + sec θ)² + (cos θ + cosec θ)²]
= [sin² θ + sec² θ + 2 sin θ sec θ + cos² θ + cosec² θ + 2 cos θ cosec θ]
= (sin² θ + cos² θ) + (sec² θ + cosec² θ) + 2 (sin θ sec θ + cos θ cosec θ)

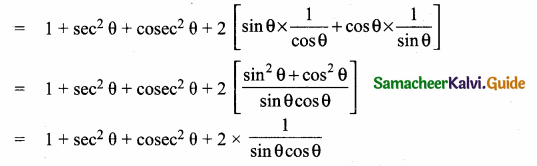
= 1 + sec² θ + cosec² θ + 2 sec θ cosec θ
= 1 + (sec θ + cosec θ)²
L.H.S = R.H.S
∴ (sin θ + sec θ)² + (cos θ + cosec θ)² = 1 + (sec θ + cosec θ)²

Question 5.
Prove the following identities.
(i) sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ = 1
(ii) \(\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{\csc \theta-1}{\csc \theta+1}\)
Answer:
(i) L.H.S = sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ

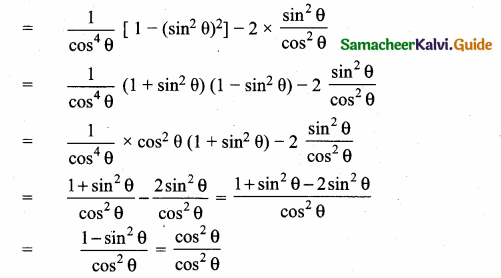
L.H.S = R.H.S
∴ sec⁴ θ (1 – sin⁴ θ) – 2 tan² θ = 1

(ii) \(\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{\csc \theta-1}{\csc \theta+1}\)

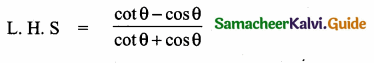
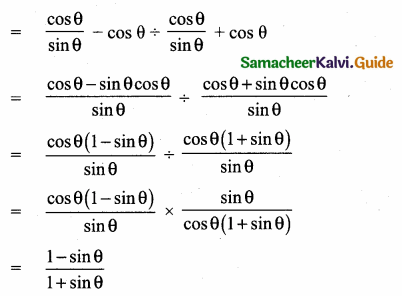
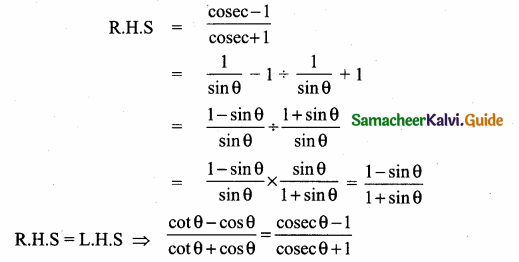
Question 6.
Prove the following identities.


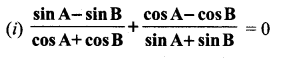
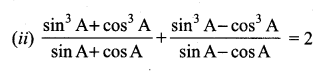
Answer:

Question 7.
(i) If sin θ + cos θ = \(\sqrt { 3 }\), then prove that tan θ + cot θ = 1.
(ii) If \(\sqrt { 3 }\) sin θ – cos θ = θ, then show that tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)
Answer:
sin θ + cos θ = \(\sqrt { 3 }\) (squaring on both sides)
(sin θ + cos θ)² = (\(\sqrt { 3 }\))²
sin² θ + cos² θ + 2 sin θ cos θ = 3
1 + 2 sin θ cos θ = 3
2 sin θ cos θ = 3 – 1
2 sin θ cos θ = 2
∴ sin θ cos θ = 1
L.H.S = tan θ + cot θ

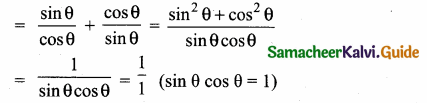
L.H.S = R.H.S ⇒ tan θ + cot θ = 1

(ii) If \(\sqrt { 3 }\) sin θ – cos θ = 0
To prove tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)
\(\sqrt { 3 }\) sin θ – cos θ = 0
\(\sqrt { 3 }\) sin θ = cos θ
\(\frac{\sin \theta}{\cos \theta}=\frac{1}{\sqrt{3}}\)
tan θ = tan 30°
θ = 30°
L.H.S = tan 3θ°
= tan3 (30°)
= tan 90°
= undefined (∝)

∴ tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)

Question 8.
(i) If \(\frac{\cos \alpha}{\cos \beta}=m\) and \(\frac{\cos \alpha}{\cos \beta}=n\) then prove that (m2 + n2) cos2 β = n2
(ii) If cot θ + tan θ = x and sec θ – sec θ – cos θ = y, then prove that (x2y)2/3 – (xy2)2/3 = 1
Answer:
(i) L.H.S = (m² + n²) cos² β

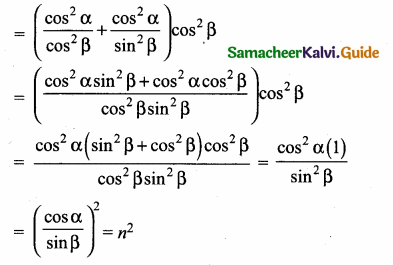
L.H.S = R.H.S ⇒ ∴ (m² + n²) cos² β = n²

(ii) Given cot θ + tan θ = x sec θ – cos θ = y
x = cot θ + tan θ
x = \(\frac{1}{\tan \theta}\) + tan θ
= \(\frac{1+\tan ^{2} \theta}{\tan \theta}\) = \(\frac{\sec ^{2} \theta}{\tan \theta}\)

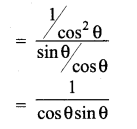
y = sec θ – cos θ
= \(\frac{1}{\cos \theta}-\cos \theta=\frac{1-\cos ^{2} \theta}{\cos \theta}\)
y = \(\frac{\sin ^{2} \theta}{\cos \theta}\)

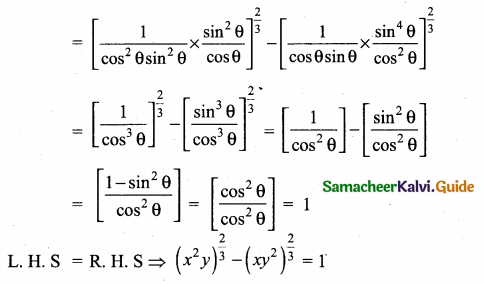
Question 9.
(i) If sin θ + cos θ = p and sec θ + cosec θ = q, then prove that q (p² – 1) = 2 p
(ii) If sin θ (1 + sin² θ) = cos² θ, then prove that cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4
Answer:
(i) p = sin θ + cos θ
p² = (sin θ + cos θ)²
= sin² θ + cos² θ + 2 sin θ cos θ = 1 + 2 sin θ cos θ
q = sec θ + cosec θ
= \(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}=\frac{\sin \theta+\cos \theta}{\sin \theta \cos \theta}\)
L.H.S = q(p² – 1)

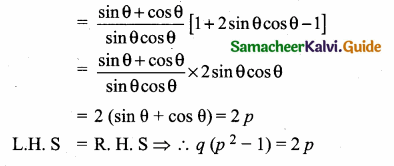
(ii) sin θ (1 + sin² θ) = cos² θ
sin θ (1 + 1 – cos² θ) = cos² θ
sin θ (2 – cos² θ) = cos² θ
Squaring on both sides,
sin² θ (2 – cos² θ)² = cos⁴ θ
(1 – cos² θ) (4 + cos⁴ θ – 4 cos² θ) = cos⁴ θ
4 cos⁴ θ – 4 cos² θ – cos⁶ θ + 4 cos⁴ θ = cos⁴ θ
4 + 5 cos⁴ θ – 8 cos² θ – cos⁶ θ = cos⁴ θ
– cos⁶ θ + 5 cos⁴ θ – cos⁴ θ – 8 cos² θ = -4
– cos⁶ θ + 4 cos⁴ θ – 8 cos² θ = -4
cos⁶ θ – 4 cos⁴ θ + 8 cos² θ = 4
Hence it is proved

Question 10.
If \(\frac{\cos \theta}{1+\sin \theta}\) = \(\frac { 1 }{ a } \), then prove that \(\frac{a^{2}-1}{a^{2}+1}\) = sin θ
Answer: