Samacheer Kalvi 10th Maths Guide Chapter 6 Trigonometry Unit Exercise 6

Students can download Maths Chapter 6 Trigonometry Unit Exercise 6 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Unit Exercise 6

Question 1.
Prove that
(i) cot² A \(\left(\frac{\sec A-1}{1+\sin A}\right)\) + sec² A \(\left(\frac{\sin A-1}{1+\sec A}\right)\) = 0
(ii) \(\frac{\tan ^{2} \theta-1}{\tan ^{2} \theta+1}\) = 1 – 2 cos² θ
Answer:


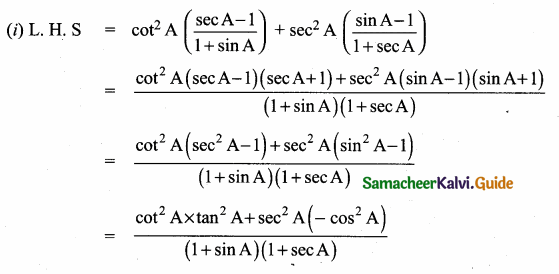
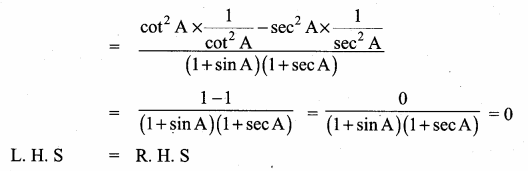
Hence it is proved

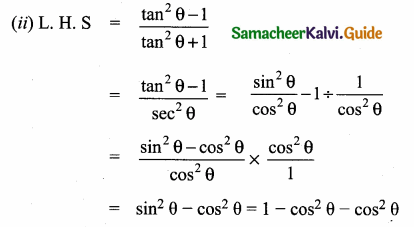
= 1 – cos² θ
L.H.S = R.H.S
Hence it is proved.

Question 2.
Prove that
\(\left(\frac{1+\sin \theta-\cos \theta}{1+\sin \theta+\cos \theta}\right)^{2}=\left(\frac{1-\cos \theta}{1+\cos \theta}\right)\)
Answer:

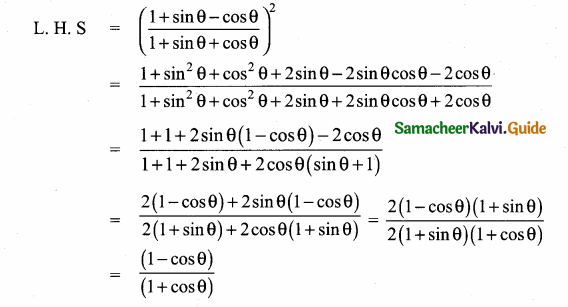
LHS = RHS
Hence it is proved

Question 3.
If x sin² θ + y cos² θ = sin θ cos θ and x sin θ = y cos θ, then prove that x² + y² = 1.
Answer:
Given x sin² θ + y cos² θ = sin θ cos θ
x sin θ = y cos θ ……..(1)
x sin³ θ + y cos³ θ = sin θ cos θ
x sin θ (sin² θ) + y cos θ (cos² θ) = sin θ cos θ
x sin θ (sin² θ) + x sin θ (cos² θ) = sin θ cos θ
x sin θ (sin² θ + cos² θ) = sin θ cos θ
x sin θ = sin θ cos θ
x = cos θ
substitute x = cos θ in (1)
cos θ sin θ = y cos θ y = sin θ
L. H. S = x² + y² = cos² θ + sin² θ = 1
L.H. S = R.H.S
Hence it is proved.

Question 4.
If a cos θ – b sin θ = c, then prove that (a sin θ + b cos θ) = ± \(\sqrt{a^{2}+b^{2}-c^{2}}\).
Answer:
Given a cos θ – b sin θ = c
Squaring on both sides
(a cos θ – b sin θ)² = c²
a² cos² θ + b² sin² θ – 2 ab cos θ sin θ = c²
a² (1 – sin² θ) + b² (1 – cos² θ) – 2 ab cos θ sin θ = c²
a² – a² sin² θ + b² – b² cos² θ – 2 ab cos θ sin θ = c²
– a² sin² θ – B² – cos² θ – 2 ab cos θ sin θ = – a² – b² + c²
a² sin² θ + b² cos² θ + 2 ab cos θ sin θ = a² + b² – c²
(a sin θ + b cos θ)² – a² + b² – c²
a sin θ + b cos θ = ± \(\sqrt{a^{2}+b^{2}-c^{2}}\)
Hence it is proved.

Question 5.
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45° . The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30° . Determine the speed at which the bird flies. (\(\sqrt { 3 }\) = 1.732)
Answer:

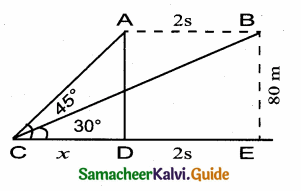
A is the initial position of the bird B is the final position of the bird Let the speed of the bird be “s”
Distance = speed × time
∴ AB = 2x
Let CD be x
∴ CE = x + 2s
In the ∆ CDA, tan 45° = \(\frac { AD }{ CD } \)
1 = \(\frac { 80 }{ x } \)
x = 80 ……..(1)
In the ∆ BCE
tan 30° = \(\frac { BE }{ CE } \)
\(\frac{1}{\sqrt{3}}\) = \(\frac { 80 }{ x+2s } \)
x + 2s = 80 \(\sqrt { 3 }\)
x = 80 \(\sqrt { 3 }\) – 2 s ………(2)
From (1) and (2) we get
80 \(\sqrt { 3 }\) – 2 s = 80
80 \(\sqrt { 3 }\) – 80 = 2 s ⇒ 80 (\(\sqrt { 3 }\) – 1) = 2 s
s = \(\frac{80(\sqrt{3}-1)}{2}\) = 40 (1.732 – 1) = 40 × 0.732 = 29.28
Speed of the flying bird = 29.28 m/sec

Question 6.
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37° at a given point. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
Answer:
Let C is the initial and D is the final position of the aeroplane.
Let the time taken by the aeroplane be “t”
∴ CD = 175 t (Distance = speed × time)

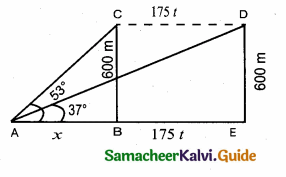
Let AB be x
∴ AE = x + 175 t
In the right ∆ ABC


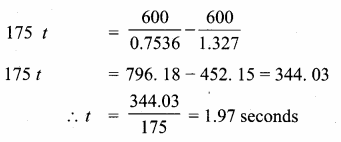
∴ Time taken is 1. 97 seconds

Question 7.
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away.
(i) How far is B to the North of A?
(ii) How far is B to the West of A?
(iii) How far is C to the North of B?
(iv) How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Answer:

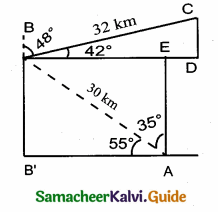
(i) To find the distance of B to the north of A
In ∆ ABB,

Distance of B to the North of A = 24. 58 km

(ii) Distance from B to the west of A is AB’
In ∆ ABB’
cos 55° = \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}\)
0.5736 = \(\frac{A B^{\prime}}{30}\)
∴ AB’ = 0.5736 × 30 = 17. 21 km
Distance of B to the West of A is 17. 21 km

(iii) Distance from C to the North of B is CD
In the right ∆ BCD, sin 42° = \(\frac { CD }{ BC } \)
0.6691 = \(\frac { BD }{ 32 } \)
∴ CD = 0.6691 × 32 = 21.41 km
Distance of C to the North B is 21. 41 km

(iv) The distance of C to the East of B is BD
In the right ∆ BDC, cos 42° = \(\frac { BD }{ BC } \)
0.7431 = \(\frac { BD }{ 32 } \)
∴ BD = 0.7431 × 32
= 23.78 km
Distance of C to the East of B is 23.78 km.

Question 8.
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is 200 \(\left(\frac{\sqrt{3}+1}{\sqrt{3}}\right)\) meters, find the height of the lighthouse
Answer:
Let A and B the position of the first ship and the second ship
Distance = 200 \(\left(\frac{\sqrt{3}+1}{\sqrt{3}}\right)\) m
Let the height of the light house CD be “h”

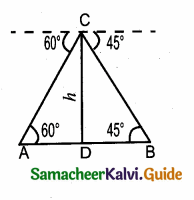
In the right ∆ ACD, tan 60° = \(\frac { CD }{ AD } \)
\(\sqrt { 3 }\) = \(\frac { h }{ AD } \)
∴ AD = \(\frac{h}{\sqrt{3}}\) ……….(1)
In the right ∆ BCD
tan 45° = \(\frac { DC }{ BD } \)
1 = \(\frac { h }{ BD } \)
∴ BD = h
Distance between the two ships = AD + BD
200 (\(\frac{\sqrt{3}+1}{\sqrt{3}}\)) = \(\frac{h}{\sqrt{3}}\) + h ⇒ 200 (\(\sqrt { 3 }\) + 1) = h + \(\sqrt { 3 }\) h
200 (\(\sqrt { 3 }\) + 1) = h(1 + \(\sqrt { 3 }\)) ⇒ h = \(\frac{200(\sqrt{3}+1)}{(1+\sqrt{3})}\)
h = 200
Height of the light house = 200 m

Question 9.
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34° . Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
Answer:
Let the height of the statue be “h” m
Let AD be x
∴ EC = h – x
In the right ∆ ABD,

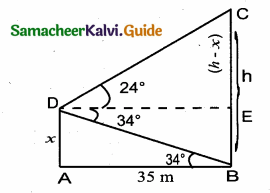
tan 34° = \(\frac { AD }{ AB } \)
0.6745 = \(\frac { x }{ 35 } \)
∴ x = 0.6745 × 35 ⇒ x = 23.61 m
In the right ∆ DEC ⇒ tan 24° = \(\frac { EC }{ DE } \)
0.4452 = \(\frac { h-x }{ 35 } \) ⇒ h – x = 0.4452 × 35
h – 23.61 = 15. 58 ⇒ h = 15.58 + 23.61 = 39.19 m
Height of the statue = 39.19 m