Samacheer Kalvi 10th Maths Model Question Paper 1 English Medium

Students can Download Samacheer Kalvi 10th Maths Model Question Paper 1 English Medium Pdf, Samacheer Kalvi 10th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamil Nadu Samacheer Kalvi 10th Maths Model Question Paper 1 English Medium

Instructions

• The question paper comprises of four parts.
• You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
• All questions of Part I, II, III and IV are to be attempted separately.
• Question numbers 1 to 14 in Part I are Multiple Choice Quèstions of one-mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and.writing the option code and the corresponding answer.
• Question numbers 15 to 28 in Part II àre two-marks questions. These are to be answered in about one or two sentences.
• Question numbers 29 to 42 in Part III are five-marks questions. These are to be answered in about three to five short sentences.
• Question numbers 43 to 44 in Part IV are eight-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Maximum Marks: 100

PART -1

I. Choose the correct answer. Answer all the questions. [14 × 1 = 14]

Question 1.
Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f : A → B given by f = {(1,4),(2, 8),(3,9),(4,10)} is a ………………… .
(1) Many-one function
(2) Identity function
(3) One-to-one function
(4) Into function
Answer:
(3) One-to-one function

Question 2.
If g = {(1,1),(2, 3),(3,5),(4,7)} is a function given by g(x) = αx + β then the values of α and β are ………………… .
(1) (-1,2)
(2) (2,-1)
(3) (-1,-2)
(4) (1,2)
Answer:
(2) (2,-1)

Question 3.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is ………………… .
(1) 2025
(2) 5220
(3) 5025
(4) 2520
Answer:
(4) 2520

Question 4.
If the sequence t₁, t₂, t₃, are in A.P. then the sequence t₆ ,t₁₂,t₁₈,… is ………………… .
(1) a Geometric progression
(2) an Arithmetic progression
(3) neither an Arithmetic progression nor a Geometric progression
(4) a constant sequence
Answer:
(2) an Arithmetic progression

Question 5.
\(\frac{x}{x^{2}-25}-\frac{8}{x^{2}+6 x+5}\) gives ………………… .
(1) \(\frac{x^{2}-7 x+40}{(x-5)(x+5)}\)
(2) \(\frac{x^{2}+7 x+40}{(x-5)(x+5)(x+1)}\)
(3) \(\frac{x^{2}-7 x+40}{\left(x^{2}-25\right)(x+1)}\)
(4) \(\frac{x^{2}+10}{\left(x^{2}-25\right)(x+1)}\)
Answer:
(3) \(\frac{x^{2}-7 x+40}{\left(x^{2}-25\right)(x+1)}\)

Question 6.
The values of a and b if 4x⁴ – 24x³ + 76x² + ax + b is a perfect square are ………………… .
(1) 100,120
(2) 10,12
(3) -120,100
(4) 12,10
Answer:
(3) -120,100

Question 7.
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is ………………… .
(1) 2.5 cm
(2) 5 cm
(3) 10 cm
(4) 5√2 cm
Answer:
(4) 5√2 cm

Question 8.
The area of triangle formed by the points (- 5, 0), (0, – 5) and (5, 0) is ………………… .
(1) 0 sq.units
(2) 25 sq.units
(3) 5 sq.units
(4) none of these
Answer:
(2) 25 sq.units

Question 9.
The value of sin²θ + \(\frac{1}{1+\tan ^{2} \theta}\) is equal to ………………… .
(1) tan²θ
(2) 1
(3) cot²θ
(4) θ
Answer:
(2) 1

Question 10.
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is ………………… .
(1) 1 : 2
(2) 1 : 4
(3) 1 : 6
(4) 1 : 8
Answer:
(2) 1 : 4

Question 11.
If the mean and coefficient of variation of a data are 4 and 87.5% then the standard deviation is ………………… .
(1) 3.5
(2) 3
(3) 4.5
(4) 2.5
Answer:
(1) 3.5

Question 12.
If α and β are the roots of the equation x² + 2x + 8 = 0 then the value of \(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\) is ………………… .
(1) \(\frac { 1 }{ 2 }\)
(2) 6
(3) \(\frac { 3 }{ 2 }\)
(4) \(\frac { -3 }{ 2 }\)
Answer:
(4) \(\frac{-3}{2}\)

Question 13.
If the points (k, 2k) (3k, 3k) and (3, 1) are collinear, then k is ………….. .
(1) \(\frac { 1 }{ 3 }\)
(2) \(\frac { -1 }{ 3 }\)
(3) \(\frac { 2 }{ 3 }\)
(4) \(\frac { -2 }{ 3 }\)
Answer:
(2) \(\frac{-1}{3}\)

Question 14.
If the variance of 14, 18, 22, 26, 30 is 32 then the variance is 28, 36, 44, 52, 60 is ………………… .
(a) 64
(b) 128
(c) 32√2
(d) 32
Answer:
(b) 128

PART – II

II. Answer any ten questions. Question No. 28 is compulsory. [10 × 2 = 20]

Question 15.
Represent the given relation {(x, y) |y = x + 3 are natural numbers < 10} by
(i) an arrow diagram (ii) a set in roster form, wherever possible
Answer:
(i)

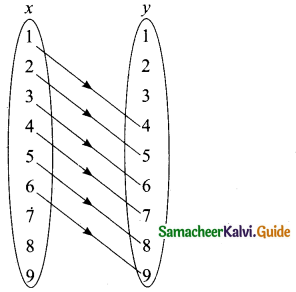
(ii) R = {(1, 4) (2, 5) (3, 6) (4, 7) (5, 8) (6, 9)}

Question 16.
If f: R → R and g : R → R are defined by f(x) = x⁵ and g(x) = x⁴ then check if f, g are one – one and fog is one – one?
Answer:
f(x) = x⁵ – It is one – one function
g(x) = x⁴ – It is one – one function
fag = f[g{x)] = f(x⁴) = (x⁴)⁵
fog = x²⁰
It is also one-one function.

Question 17.
Find the first five terms of the following sequence.
a₁ = 1, a₂, a_n = \(\frac{a_{n-1}}{a_{n-2}+3}\) ; n ≥ 3 ; n ∈ N
Answer:
The first two terms of this sequence are given by a₁ = 1, a₂ = 1. The third term a₃ depends on the first and second terms.

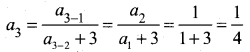
Similarly the fourth term a₄ depends upon a₂ and a₃.

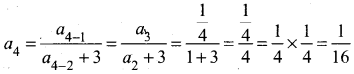
In the same way, the fifth term a₅ can be calculated as

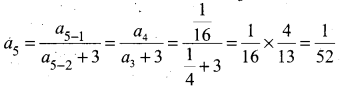
Therefore, the first fie terms of the sequence are 1,1, \(\frac{1}{4}, \frac{1}{16}, \frac{1}{52}\)

Question 18.
If 1³ + 2³ + 3³ +. . . .+ k³ = 44100 then find 1+ 2 + 3 + …. + k
Answer:
1³ + 2³ + 3³ + ………. + K³ = 44100
\(\left[\frac{k(k+1)}{2}\right]^{2}\) = 44100
\(\frac{k(k+1)}{2}\) = \(\sqrt{44100}\) = 210
1 + 2 + 3 + …….. + k = \(\frac{k(k+1)}{2}\)

Question 19.
Find the LCM of the polynomials a² + 4a – 12, a² – 5a + 6 whose GCD is a – 2
Answer:
p(x) = a² + 4a – 12
= a² + 6a – 2a – 12

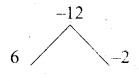
= a (a + 6) – 2(a + 6)
= (a + 6) (a – 2)
g(x) = a² – 5a + 6
= a² – 3a – 2a + 6

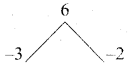
= a(a – 3) – 2 (a – 3)
= (a – 3) (a – 2)
L.C.M. = \(\frac{p(x) \times g(x)}{\text { G.C.D. }}\)
= \(\frac{(a+6)(a-2) \times(a-3)(a-2)}{(a-2)}\)
= (a + 6) (a – 3) (a – 2)

Question 20.
Find the value of ‘k’ whose roots of the equation kx² + (6k + 2)x + 16 = 0 are real and equal.
Answer:

Here a = k, b = 6k+ 2 ; c = 16
Since the equation has real and equal roots .
A = 0
b² – 4ac = 0
(6k + 2)² – 4(k)(16) = 0
36k² + 4 + 24k – 4(k) (16) = 0
36k² – 40k + 4 = 0
(÷ by 4) ⇒ 9k² – 10k + 1 = 0
9k² – 9k – k + 1 = 0
9k(k – 1) – 1(k – 1) = 0
(k – 1) (9k – 1) = 0
k – 1 = 0 or 9k – 1 = 0 ⇒ k = 1 or k = \(\frac { 1 }{ 9 }\)
The value of k = 1 or \(\frac { 1 }{ 9 }\)

Question 21.
Find the value of a, b, c, d, x, y from the following matrix equation.
\(\left( \begin{matrix} d & 8 \\ 3b & a \end{matrix} \right) +\left( \begin{matrix} 3 & a \\ -2 & -4 \end{matrix} \right) =\left( \begin{matrix} 2 & 2a \\ b & 4c \end{matrix} \right) +\left( \begin{matrix} 0 & 1 \\ -5 & 0 \end{matrix} \right) \)
Answer:
First, we add the two matrices on both left, right hand sides to get
\(\left( \begin{matrix} d+3 & 8+a \\ 3b-2 & a-4 \end{matrix} \right) =\left( \begin{matrix} 2 & 2a+1 \\ b-5 & 4c \end{matrix} \right) \)
Equating the corresponding elements of the two matrices, we have
d + 3 = 2 gives d = -1
8 + a = 2a + 1 gives a = 7
3b – 2 = b – 5 gives b = \(\frac { -3 }{ 2 }\)
Substituting a = 7 in a – 4 = 4c gives c = \(\frac { 3 }{ 4 }\)
Therefore, a = 7, b = \(\frac { -3 }{ 2 }\) ,c = \(\frac { 3 }{ 4 }\) , d = -1.

Question 22.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
Answer:

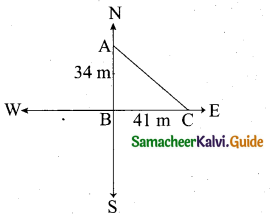
In the right ∆ABC,
By Pythagoras theorem
AC² = AB² + BC² = 34² + 41²
= 1156 + 1681 = 2837
AC = √2837
= 53.26 m
Through A one must walk (34m + 41m) 75 m to reach C.
The difference in Distance = 75 – 53.26
= 21.74 m

Question 23.
If the points A(-3, 9), B(a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.
Answer:
Since the three points are collinear
Area of a ∆ = 0
\(\frac { 1 }{ 2 }\)[(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]

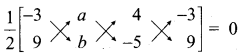
\(\frac { 1 }{ 2 }\)[(-36 – 5a 4- 36) – (9a + 46 + 15)] = 0
-36 – 5a + 36 – 9a -4b – 15 = 0
-7b – 14a + 21=0
(÷ by 7) – b – 2a + 3 = 0
2a + b – 3 = 0

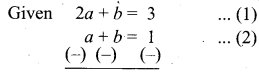
Subtract (1) and (2) ⇒ a = 2
Substitute the value of a = 2 in (2) ⇒ 2 + 6 = 1
b = 1 – 2 = -1
The value of a = 2 and b = -1

Question 24.
Prove that \(\frac{\sin A}{1+\cos A}+\frac{\sin A}{1-\cos A}\) = 2 cosec A.
Answer:

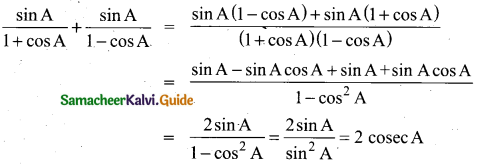
Question 25.
The probability that atleast one of A and B occur is 0.6. If A and B occur simultaneously with probability 0.2, then find P(Ā) + P(B̄).
Answer:
Here p(A ∪ B) = 0.6, p(A ∩ B) = 0.2
p(A ∪ B) = p(A) + p(B) – p(A ∩ B)
0.6 = p(A) + P(B) – 0.2
∴ p(A) + p(B) = 0.8
P(Ā) + P(B̄) = 1 – p(A) + 1 – p(B)
= 2 – [p(A) + p(B)]
= 2 – 0.8 = 1.2

Question 26.
If n = 10, X̄ = 12 and Σx² = 1530, then calculate the coefficient of variation.
Answer:
Given that n = 10, X̄ = \(\frac{\Sigma x}{n}\) = 12, Σx² = 1530

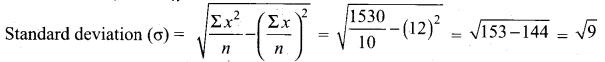
(σ) = 3
coefficient of variation = \(\frac{\sigma}{\bar{x}} \times 100\) ⇒ \(\frac{3}{12} \times 100=25\)
∴ coefficient of variation = 25

Question 27.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 14 cm.
Answer:
Given, Edge of the cube = 14 cm
The largest circular cone is cut out from the cube.
Radius of the cone (r) = \(\frac { 14 }{ 2 }\) = 7 cm
Height of the cone (h) = 14 cm
Volume of a cone = \(\frac { 1 }{ 3 }\) πr²h cu. units
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 14 cm³
= \(\frac{22 \times 7 \times 14}{3}\) cm³
∴ Volume of a cone = 718.67 cm³

Question 28.
Find the sum of the first 40 terms of the series 1² – 2² + 3² – 4² + …..
Answer:
The given series is 1² – 2² + 3² – 4² + …. 40 terms
Grouping the terms we get,
(1² – 2²) + (3² – 4²) + (5² – 6²) + ………… 20 terms
(1 – 4) + (9 – 16) + (25 – 36) + …………. 20 terms
(-3) + (-7) + (-11) + ………… 20 term
This is an A.P
Here a = – 3, d = – 7 – (- 3) = – 7 + 3 = -4, n = 20
S_n = \(\frac { n }{ 2 }\)[2a + (n – 1)d]
S₂₀ = \(\frac { 20 }{ 2 }\)[2(-3) + 19(-4)]
= 10 (- 6 – 76) = 10 (- 82) = – 820
∴ Sum of 40 terms of the series is = 820.

PART – III

III. Answer any ten questions. Question No. 42 is compulsory. [10 × 5 = 50]

Question 29.
Find x if gff(x) = fgg(x), given f(x) = 3x + 1 and g(x) = x + 3.

Question 30.
In a G.P the product of three consecutive terms is 27 and the sum of the product of two terms taken at a time is \(\frac{57}{2}\).Find the three terms.

Question 31.
The 13th term of an A.P. is 3 and the sum of first 13 terms is 234. Find the common difference and the sum of first 21 terms.

Question 32.
If Sn = (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + ………… n terms then prove that (x – y)S_n = \(\left[\frac{x^{2}\left(x^{n}-1\right)}{x-1}-\frac{y^{2}\left(y^{n}-1\right)}{y-1}\right]\)

Question 33.
Two women together took 100 eggs to a market, one had more than the other. Both sold them for the same sum of money. The first then said to the second: “If I had your eggs, I would have earned ₹15”, to which the second replied: “If I had your eggs, I would have earned ₹6 \(\frac { 2 }{ 3 }\) ”. How many eggs did each had in the beginning?

Question 34.
If the roots of (a – b)x² + (b – c)x + (c – a) = 0 are real and equal, then prove that b, a, c are in arithmetic progression.

Question 35.
A circle is inscribed in AABC having sides 8 cm, 10 cm and 12 cm as shown in figure, Find AD, BE and CF.

Question 36.
The line joining the points A(0,5) and B(4,1) is a tangent to a circle whose centre C is at the point (4, 4) find
(i) the equation of the line AB.
(ii) the equation of the line through C which is perpendicular to the line AB.
(iii) the coordinates of the point of contact of tangent line AB with the circle.

Question 37.
If sin θ (1 + sin²θ) = cos²θ , then prove that cos⁶θ – 4 cos⁴θ + 8 cos²θ = 4

Question 38.
A toy is in the shape of a cylinder surmounted by a hemisphere. The height of the toy is 25 cm. Find the total surface area of the toy if its common diameter is 12 cm.

Question 39.
Find the coefficient of variation of 24, 26, 33, 37, 29, 31.

Question 40.
The probability that A, B and C can solve a problem are \(\frac { 4 }{ 5 }\), \(\frac { 2 }{ 3 }\) and \(\frac { 3 }{ 7 }\) respectively. The probability of the problem being solved by A and B is \(\frac { 8 }{ 15}\),B and C is \(\frac { 2 }{ 7 }\) , A and C is \(\frac { 12 }{ 13 }\) . The probability of the problem being solved by all the three is \(\frac { 8 }{ 35 }\). Find the probability that the problem can be solved by atleast one of them.

Question 41.
Verify that (AB)_T = B_TA_T if A = \(\left( \begin{matrix} 2 & 3 & -1 \\ 4 & 1 & 5 \end{matrix} \right) \) and B = \(\left( \begin{matrix} 1 & -2 \\ 3 & -3 \\ 2 & 6 \end{matrix} \right) \)

Question 42.
A function f(-3, 7) → R is defined as follows

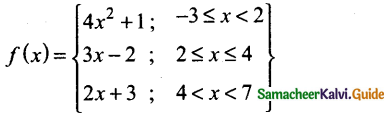
Find (i) 5f(1) -3f(-2) (ii) 3f(-3) + 4 f(4) (iii) \(\frac{7 f(3)-f(-1)}{2 f(6)-f(1)}\)

PART – IV

IV. Answer all the questions. [2 × 8 = 16]

Question 43.
(a) Construct a ∆PQR such that QR = 6.5 cm, ∠P = 60° and the altitude from P to QR is of length 4.5 cm.

[OR]

(b) Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.

Question 44.
(a) Draw the graph of y = x² + x and hence solve x² + 1 = 0

[OR]

(b) Solve graphically (x + 2) (x + 4) = 0