Students can Download Samacheer Kalvi 10th Maths Model Question Paper 4 English Medium Pdf, Samacheer Kalvi 10th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamil Nadu Samacheer Kalvi 10th Maths Model Question Paper 4 English Medium
Instructions
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 14 in Part I are Multiple Choice Quèstions of one-mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and.writing the option code and the corresponding answer.
- Question numbers 15 to 28 in Part II àre two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 29 to 42 in Part III are five-marks questions. These are to be answered in about three to five short sentences.
- Question numbers 43 to 44 in Part IV are eight-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Maximum Marks: 100
PART – I
I. Choose the correct answer. Answer all the questions. [14 × 1 = 14]
Question 1.
If A = {1,2}, B = {1, 2, 3, 4}, C = {5,6} and D = {5, 6, 7, 8} then state which of the following statement is true ………….. .
(1) (A × C) ⊂ (B × D)
(2) (B × D) ⊂ (A × C)
(3) (A × B) ⊂ (A × D)
(4) (D × A) ⊂ (B × A)
Answer:
(1) (A × C) ⊂ (B × D)
![]()
Question 2.
If f(x) = 2x2 and g(x) = \(\frac { 1 }{ 3x }\), then jog is ………….. .
(1) \(\frac{3}{2 x^{2}}\)
(2) \(\frac{2}{3 x^{2}}\)
(3) \(\frac{2}{9 x^{2}}\)
(4) \(\frac{1}{6 x^{2}}\)
Answer:
(3) \(\frac{2}{9 x^{2}}\)
Question 3.
Given F1 = 1,F2 = 3 and Fn = Fn-1 + Fn-2 then F5 is ………….. .
(1) 3
(2) 5
(3) 8
(4) 11
Answer:
(4) 11
Question 4.
The value of (13 + 23 + 33 +. . . .+ 153) – (1 + 2 + 3 +….+ 15) is ………….. .
(1) 14400
(2) 14200
(3) 14280
(4) 14520
Answer:
(3) 14280
Question 5.
The solution of the system x + y – 3z = -6 , – 7y + 7z = 7, 3z = 9 is ………….. .
(1) x = 1, y = 2, z = 3
(2) x = -1, y = 2, z = 3
(3) x = -1, y = -2, z = 3
(4) x = 1, y = 2, z = 3
Answer:
(1) x = 1, y = 2, z = 3
Question 6.
If number of columns and rows are not equal in a matrix then it is said to be a ………….. .
(1) diagonal matrix
(2) rectangular matrix
(3) square matrix
(4) identity matrix
Answer:
(2) rectangular matrix
Question 7.
The slope of the line which is perpendicular to a line joining the points (0, 0) and (-8, 8) is ………….. .
(1) -1
(2) 1
(3) \(\frac { 1 }{ 3 }\)
(4) -8
Answer:
(2) 1
![]()
Question 8.
If sin θ + cos θ = a and sec θ + cosec θ = 6, then the value of b (a2 – 1} is equal to ………….. .
(1) 2 a
(2) 3 a
(3) 0
(4) 2 ab
Answer:
(1) 2 a
Question 9.
If two solid hemispheres of same base radius r units are joined together along their bases, then curved surface area of this new solid is ………….. .
(1) 4π r2 sq. units
(2) 6π r2 sq. units
(3) 3π r2 sq. units
(4) 8π r2 sq. units
Answer:
(1) 4π r2 sq. units
Question 10.
The standard deviation of a data is 3. If each value is multiplied by 5 then the new variance is ………….. .
(1) 3
(2) 15
(3) 5
(4) 225
Answer:
(4) 225
Question 11.
Kamalam went to play a lucky draw contest. 135 tickets of the lucky draw were sold. If the probability of Kamalam winning is \(\frac { 1 }{ 9 }\), then the number of tickets bought by Kamalam is ………….. .
(1) 5
(2) 10
(3) 15
(4) 20
Answer:
(3) 15
Question 12.
If α and β are the zeros of the polynomial p(x) = 4x2 + 3x + 7 then \(\frac{1}{\alpha}+\frac{1}{\beta}\) is equal to …… .
(1) \(\frac{7}{3}\)
(2) \(-\frac{7}{3}\)
(3) \(\frac{3}{7}\)
(4) \(-\frac{3}{7}\)
Answer:
(4) \(-\frac{3}{7}\)
Question 13.
The common ratio of the G.P. am-n, am, am + n is ………….. .
(1) am
(2) a-m
(3) an
(4) an
Answer:
(3) an
Question 14.
If the circumference at the base of a right circular cone and the slant height are 120π cm and 10 cm respectively, then the curved surface area of the cone is equal to ………….. .
(1) 1200 π cm2
(2) 600 π cm2
(3) 300 π cm2
(4) 600 π m2
Answer:
(2) 600 π cm2
![]()
PART – II
II. Answer any ten questions. Question No. 28 is compulsory. [10 × 2 = 20]
Question 15.
Let A = {1,2, 3, 4} and B = N . Let f: A → B be defined by f(x) = x3 then,
(i) find the range of f
(ii) identify the type of function
Answer:
A = {1,2,3,4}
B = (1,2,3,4,5, ………}
f(x) = x3
f(1) = 13 = 1
f(2) = 23 = 8
f(3) = 33 = 27
f(4) = 43 = 64
(i) Range = {1, 8,27, 64)
(ii) one -one and into function.
Question 16.
If f(x) = 2x -1, g (x) = \(\frac{x+1}{2}\), show that fog = gof = x
Answer:
f(x) = 2x – 1 : g(x) = \(\frac{x+1}{2}\)
fog = f[g(x)]
= \(f\left[\frac{x+1}{2}\right]\)
= \(2\left(\frac{x+1}{2}\right)-1\)
= x + 1 – 1
= x
gof = g[f(x)]
= g (2x – 1)
= \(\frac{2 x-1+1}{2}\)
= \(\frac{2 x}{2}\)
= x
∴ fog = gof = x
Hence it is proved.
Question 17.
Determine the general term of an A.P. whose 7th term is -1 and 16th term is 17.
Answer:
Let the AP. be t1, t2, t3, t4, ………
It is given that t7 = -1 and t16 = 17
a + (7 – 1)d = -1 and a + (16 – 1) d = 17
a + 6d = – 1 ……. (1)
a + 15d = 17 ……… (2)
Subtracting equation (1) from equation (2), we get 9d = 18 ⇒ d = 2
Putting d = 2 in equation (1), we get a + 12 = -1 So, a = -13
Hence, general term tn = a + (n – 1) d = -13 + (n – 1) × 2 = 2n – 15
Question 18.
Find x so that x + 6, x + 12 and x + 15 are consecutive terms of a Geometric Progression.
Answer:
\(\frac{t_{2}}{t_{1}}=\frac{x+12}{x+6}\), \(\frac{t_{3}}{t_{2}}=\frac{x+15}{x+12}\)
Since it is a G.P.
\(\frac{x+12}{x+6}=\frac{x+15}{x+12}\)
(x + 12)2 = (x + 6) (x + 15)
x2 + 24x + 144 = x2 + 21x + 90
3x = -54 ⇒ x = \(\frac{-54}{3}\) = – 18
![]()
Question 19.
Find the excluded values of the expression \(\frac{x^{2}+6 x+8}{x^{2}+x-2}\)
Answer:
x2 + 6x + 8 = (x + 4)(x + 2)
x2 + x – 2 = (x + 2)(x – 1)
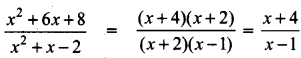

The expression \(\frac{x+4}{x-1}\) is undefined
when x – 1 = 0 ⇒ x = 1
The excluded value is 1
Question 20.
Solve 3p2 + 2√5p – 5 = 0 by formula method.
Answer:
Compute 3p2 + 2√5p – 5 = 0 with the standard form ax2 + bx + c = O
a = 3, b = 2√5, c = -5
p = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Substituting the values of a, b and e in the formula we get,
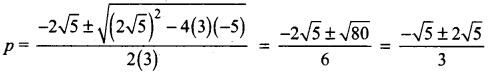
Therefore, x = \(\frac{\sqrt{5}}{3},-\sqrt{5}\)
Question 21.
Write the expression \(\frac{\alpha+3}{\beta}+\frac{\beta+3}{\alpha}\) in terms of α + β and αβ.
Answer:

Question 22.
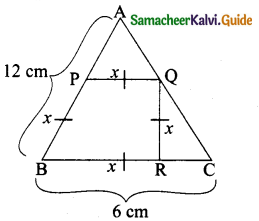
Rhombus PQRB is inscribed in ∆ABC such that ∠B is one of its angle. P, Q and R lie on AB, AC and BC respectively. If AB = 12 cm and BC = 6 cm, find the sides PQ, RB of the rhombus.
Answer:
Let the side of the rhombus be “x”. Since PQRB is a Rhombus PQ || BC
By basic proportionality theorem
\(\frac{A P}{A B}=\frac{P Q}{B C} \Rightarrow \frac{12-x}{12}=\frac{x}{6}\)
12x = 6(12 – x)
12x = 72 – 6x
12x + 6x = 72
18x = 72 ⇒ x = \(\frac { 72 }{ 18 }\) = 4
Side of a rhombus = 4cm
PQ = RB = 4cm
![]()
Question 23.
Find the equation of a straight line which is parallel to the line 3x – 7y = 12 and passing through the point (6,4)
Answer:
Equation of the straight line, parallel to 3x – 7y – 12 = 0 is 3x – 7y + k= O
Since it passes through the point (6,4)
3(6) – 7(4) + k = 0
k = 28 – 18= 10
Therefore, equation of the required straight line is 3x – 7y + 10 = 0.
Question 24.
Prove that \(\frac{\tan ^{2} \theta-1}{\tan ^{2} \theta+1}\) = 1 – 2 cos2 θ
Answer:
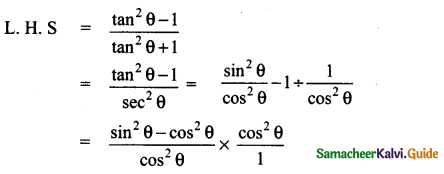
= sin2 θ – cos2 θ = 1 – cos2 θ – cos2 θ
= 1 – 2 cos2θ
L.H.S = R.H.S
Hence it is proved.
Question 25.
The standard deviation and coefficient of variation of a data are 1.2 and 25.6 respectively. Find the value of mean.
Answer:
Standard deviation (σ) = 1.2
Coefficient of variation = 25.6
\(\frac{\sigma}{x} \times 100\) = 25.6
\(\frac{1.2}{\bar{x}} \times 100\) = 25.6 ⇒ 25.6 × x̄ = 1.2 × 100
x̄ = \(\frac{120}{25.6}=\frac{120 \times 10}{256}\) = 4.687 = 4.69
Value of mean = 4.69
![]()
Question 26.
Three dice are thrown simultaneously. Find the probability of getting the same number.
Answer:
Sample space = {(1, 1, 1) (1, 1,2) (1, 1,3). .. . (6,6, 6)}
n(S) = 216
Let A be the event of getting the same number on all the three dice
A = {(1,1,1),(2,2,2),(3,3,3),(4,4,4)(5,5,5)(6,6,6fl
n(A) = 6
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{6}{216}=\frac{1}{36}\)
Question 27.
If the curved surface area of a solid hemisphere is 2772 sq. cm, then find its total surface area.
Answer:
Curved surface area ofa hemisphere = 2772 sq.cm
2πr2 = 2772
πr2 = \(\frac{2772}{2}\) = 1386
T.S.A of the hemisphere = 3πr2 sq. units
= 3 × 1386 cm2
= 4158 cm2
Question 28.
Which term of the geometric sequence 5,2, \(\frac{4}{5}, \frac{8}{25} \cdots \text { is } \frac{128}{15625}\) ?
Answer:
The given G.P is 5,2, \(\frac{4}{5}, \frac{8}{25} \cdots \text { is } \frac{128}{15625}\)
Here a = 5, r = \(\frac { 2 }{ 5 }\)
tn = \(\frac{128}{15625}\)
a.rn-a = \(\frac{128}{15625}\)
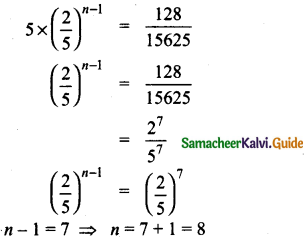
![]()
PART – III
III. Answer any ten questions. Question No. 42 is compulsory. [10 × 5 = 50]
Question 29.
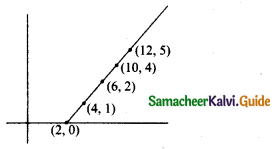
Let f: A → B be a function defined by f(x) = \(\frac { x }{ 2 }\) – 1, where A = {2,4,6,10,12}, B = {0,1,2,4,5,9} . Represent f by
(i) set of ordered pairs
(ii) a table
(iii) an arrow diagram
(iv) a graph
Answer:
(i) f = {(2,0)(4, 1)(6,2)(10,4)(12,5)
(ii)

(iii)
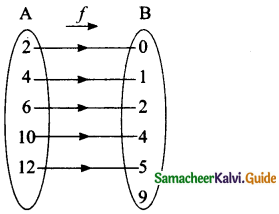
(iv)
Question 30.
Given f(x) = x – 1, g(x) = 3x + 1 and h(x) = x2 show that (fog)oh = fo(goh)
Question 31.
The product of three consecutive terms of a Geometric Progression is 343 and their sum is \(\frac{91}{3}\) Find the three terms.
Question 32.
Find the sum of all natural numbers between 602 and 902 which are not divisible by 4?
Question 33.
There are 12 pieces of five, ten and twenty rupee currencies whose total value is ₹105. But when first 2 sorts are interchanged in their numbers its value will be increased by ₹20. Find the number of currencies in each sort.
![]()
Question 34.
A passenger train takes 1 hr more than an express train to travel a distance of 240 km from Chennai to Virudhachalam. The speed of passenger train is less than that of an express train by 20 km per hour. Find the average speed of both the trains.
Question 35.
ABCD is a trapezium in which AB || DC and P,Q are points on AD and BC respectively, such that PQ || DC if PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
Question 36.
Find the equation of the perpendicular bisector of the line joining the points A(-4,2) and B(6, -4).
Question 37.
From the top of a tower 50 m high, the angles of depression of the top and bottom of a tree and observed to be 30° and 45° respectively. Find the height of the tree. ( √3 = 1.732)
Question 38.
A hemispherical bowl is filled to the brim with juice. The juice is poured into a cylindrical vessel whose radius is 50% more than its height. If the diameter is same for both the bowl and the cylinder then find the percentage of juice that can be transferred from the bowl into the cylindrical 1 vessel.
Question 39.
A box contains cards numbered 3, 5, 7,9,… 35,37. A card is drawn at random from the box. Find the probability that the drawn card have either multiples of 7 or a prime number.
Question 40.
The function f: [-7, 6] → R is defined as follows.
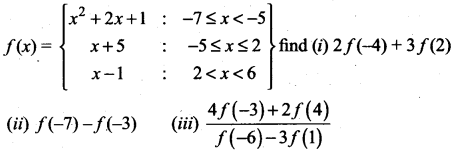
![]()
Question 41.
The denominator of a fraction is 4 more than twice the numerator. When both the numerator and denominator are decreased by 6, then the denominator becomes 12 times the numerator determine the fraction.
Question 42.
If for distribution Σx – 7 = 3 ; (Σx – 7)2 = 57 and total number of the item is 20; find the mean and standard deviation.
PART – IV
IV. Answer all the questions. [2 × 8 = 16]
Question 43.
(a) Draw a circle of diameter 6 cm from a point P, which is 8 cm away from its centre. Draw the two tangents PA and PB to the circle and measure their lengths.
[OR]
(b) Construct a triangle ∆PQR such that QR = 5 cm, ∠P = 30° and the altitude from P to QR is of length 4.2 cm.
![]()
Question 44.
(a) Draw the graph of y = x2 and hence solve x2 – 4x – 5 = 0.
[OR]
(b) Draw the graph of y = x2 + 3x + 2 and use it to solve the equation x2 + 2x + 4 = 0.