Samacheer Kalvi 10th Maths Model Question Paper 5 English Medium

Students can Download Samacheer Kalvi 10th Maths Model Question Paper 5 English Medium Pdf, Samacheer Kalvi 10th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamil Nadu Samacheer Kalvi 10th Maths Model Question Paper 5 English Medium

Instructions

• The question paper comprises of four parts.
• You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
• All questions of Part I, II, III and IV are to be attempted separately.
• Question numbers 1 to 14 in Part I are Multiple Choice Quèstions of one-mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and.writing the option code and the corresponding answer.
• Question numbers 15 to 28 in Part II àre two-marks questions. These are to be answered in about one or two sentences.
• Question numbers 29 to 42 in Part III are five-marks questions. These are to be answered in about three to five short sentences.
• Question numbers 43 to 44 in Part IV are eight-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Maximum Marks: 100

PART – I

I. Choose the correct answer. Answer all the questions. [14 × 1 =14]

Question 1.
The range of the relation R = {(x, x²) x is a prime number less than 13} is ………… .
(1) {2, 3, 5, 7}
(2) (2, 3, 5, 7, 11}
(3) {4,9,25,49, 121}
(4) {1, 4, 9, 25, 49, 121}
Answer:
(3) {4,9,25,49, 121}

Question 2.
If g = {(1,1),(2, 3),(3,5),(4,7)} is a function given by g(x) = αx + β then the values of α and β are ……….. .
(1) (-1,2)
(2) (2,-1)
(3) (-1,-2)
(4) (1,2)
Answer:
(2) (2,-1)

Question 3.
The sum of the exponents of the prime factors in the prime factorization of 1729 is ……….. .
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(3) 3

Question 4.
The next term of the sequence \(\frac{3}{16}, \frac{1}{8}, \frac{1}{12}, \frac{1}{18}\) is ……….. .
(1) \(\frac{1}{24}\)
(2) \(\frac{1}{27}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{1}{81}\)
Answer:
(2) \(\frac{1}{27}\)

Question 5.
If (x – 6) is the HCF of x² – 2x – 24 and x² – kx – 6 then the value of k is ……….. .
(1) 3
(2) 5
(3) 6
(4) 8
Answer:
(2) 5

Question 6.
The solution of (2x – 1)² = 9 is equal to ……….. .
(1) -1
(2) 2
(3) -1,2
(4) None of these
Answer:
(3) -1,2

Question 7.
In a given figure ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is ……….. .

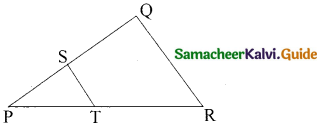
(1) 25 : 4
(2) 25 : 7
(3) 25 :11
(4) 25 : 13
Answer:
(1) 25 : 4

Question 8.
The slope of the line joining (12, 3), (4, a) is \(\frac { 1 }{ 8 }\). The value of ‘a’ is ……….. .
(1) 1
(2) 4
(3) -5
(4) 2
Answer:
(4) 2

Question 9.
If sin θ + cos θ = a and sec θ + cosec θ = b, then the value of b (a² – 1) is equal to ……….. .
(1) 2 a
(2) 3 a
(3) 0
(4) 2 ab
Answer:
(1) 2 a

Question 10.
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is ……….. .
(1) 60π cm²
(2) 68π cm²
(3) 120π cm²
(4) 136π cm²
Answer:
(4) 136π cm²

Question 11.
The sum of all deviations of the data from its mean is ……….. .
(1) always positive
(2) always negative
(3) zero
(4) non-zero integer
Answer:
(3) zero

Question 12.
If \(\left( \begin{matrix} x+y & x-y \\ 7 & 6 \end{matrix} \right) =\left( \begin{matrix} 10 & 2 \\ 7 & z \end{matrix} \right) \) then x, y, z are ……….. .
(1) 4, 6, 6
(2) 6, 6, 4
(3) 6, 4, 6
(4) 4, 4, 6
Answer:
(3) 6, 4, 6

Question 13.
If the n^th term of a sequence is 100n + 10 then the sequence is ……….. .
(1) an A.P.
(2) a G.P.
(3) a constant sequence
(4) neither A.P. nor G.P.
Answer:
(1) an A.P.

Question 14.
Probability of getting 3 heads or 3 tails in tossing a coin 3 times is ……….. .
(1) \(\frac { 1 }{ 8 }\)
(2) \(\frac { 1 }{ 4 }\)
(3) \(\frac { 3 }{ 8 }\)
(4) \(\frac { 1 }{ 2 }\)
Answer:
(2) \(\frac { 1 }{ 4 }\)

PART – II

II. Answer any ten questions. Question No. 28 is compulsory. [10 × 2 = 20]

Question 15.
Let A = {x ∈ W / x < 2}, B = {x ∈ N / 1 < x ≤ 4} and C = {3, 5} find the value of (A × C) ∪ (B × C)
Answer:
A × C = {0,1} × {3,5}
= {(0,3 (0,5) (1,3) (1,5)}
B × C= (2,3,4) × (3,5)
= {(2,3) (2,5) (3,3) (3,5) (4,3) (4,5)}
(A × C) ∪ (B × C) = {(0,3) (0,5) (1,3) (1,5) (2,3) (2,5) (3,3) (3,5) (4,3) (4,5)}

Question 16.
Find k if fof(k) = 5 where f(k) = 2k – 1.
Answer:
fof(k) = f(f(k)) = 2(2k – 1)-1 = 4k – 3.
Thus, fof(k) = 4k – 3
But, it is given that fof(k) = 5
∴ 4k – 3 = 5 ⇒ k = 2.

Question 17.
Find the sum of the following 6 + 13 + 20 +…. + 97
Answer:
Here a = 6, d = 13 – 6 = 7, l = 97
n = \(\frac{l-a}{d}+1\)
= \(\frac{97-6}{7}+1\) = \(\frac{91}{7}+1\) = 13 + 1 = 14
S_n = \(\frac{n}{2}\)(a + l)
S_n = \(\frac{14}{2}\)(6 + 97) = 7 × 103 = 721

Question 18.
Rekha has 15 square colour papers of sizes 10 cm, 11 cm, 12 cm, …,.24 cm. How much area can be decorated with these colour papers?
Answer:
Area of 15 square colour papers
= 10² + 11² + 12² + …. + 24²
= (1² + 2² + 3² + …. + 24²) – (1² + 2² + 9²)
= \(\frac{24 \times 25 \times 49}{6}-\frac{9 \times 10 \times 19}{6}\)
=4 × 25 × 49 – 3 × 5 × 19
= 4900 – 285
= 4615
Area can be decorated is 4615 cm²

Question 19.
Simplify \(\frac{x+2}{4 y} \div \frac{x^{2}-x-6}{12 y^{2}}\)
Answer:

x² – x – 6 = (x – 3) (x + 2)
= \(\frac{x+2}{4 y} \div \frac{x^{2}-x-6}{12 y^{2}}=\frac{x+2}{4 y}+\frac{(x-3)(x+2)}{12 y^{2}}\)
= \(\frac{(x+2)}{4 y} \times \frac{12 y^{2}}{(x-3)(x+2)}\)
= \(\frac{3 y}{x-3}\)

Question 20.
Solve \(\frac{x}{x-1}+\frac{x-1}{x}=2 \frac{1}{2}\)
Answer:
Let y = \(\frac{x}{x-1}\) then \(\frac{1}{y}=\frac{x-1}{x}\)
Therefore, \(\frac{x}{x-1}+\frac{x-1}{x}=2 \frac{1}{2}\) becomes \(y+\frac{1}{y}=\frac{5}{2}\)
2y² – 5y + 2 = 0 then, y = \(\frac{1}{2}, 2\)
\(\frac{x}{x-1}=\frac{1}{2}\) we get, 2x = x – 1 implies x = – 1
\(\frac{x}{x-1}=2\) we get, x = 2x – 2 implies x = 2
∴ The roots are x = -1, 2

Question 21.
Construct a 3 × 3 matrix whose elements are given by a_ij = |i – 2j|
Answer:
a_ij = |i – 2j|
The general 3 × 3 matrices is
A = \(\left( \begin{matrix} { a }_{ 11 } & { a }_{ 12 } & { a }_{ 13 } \\ { a }_{ 21 } & { a }_{ 22 } & { a }_{ 23 } \\ { a }_{ 31 } & { a }_{ 32 } & { a }_{ 33 } \end{matrix} \right)\)
a₁₁ = |1 – 2(1)| = |1 – 2| = |-1| = 1
a₁₂ = |1 – 2(2)| = |1 – 4| = |-3| = 3
a₁₃ = |1 – 2(3)| = |1 – 6| = |-5| = 5
a₂₁ = |2 – 2(1)| = |2 – 2| = 0
a₂₂ = |2 – 2(2)| = |2 – 4| = |-2| = 2
a₂₃ = |2 – 2(3)| = |2 – 6| = |-4| = 4
a₃₁ = |3 – 2(1)| = |3 – 2| = |1| = 1
a₃₂ = |3 – 2(2)| = |3 – 4| = |-1| = 1
a₃₃ = |3 – 2(3)| = |3 – 6| = |-3| = 3
The required matrix A = \(\left[ \begin{matrix} 1 & 3 & 5 \\ 0 & 2 & 4 \\ 1 & 1 & 3 \end{matrix} \right] \)

Question 22.
The length of the tangent to a circle from a point P, which is 25 cm away from the centre is 24 cm. What is the radius of the circle?
Answer:

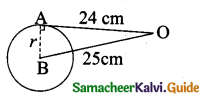
Let the radius AB be r. In the right ∆ ABO,
OB² = OA² + AB²
25² = 24² + r²
25² – 24² = r²
(25 + 4) (25 – 24) = r²
r = √49 = 7
Radius of the circle = 7 cm

Question 23.
If the straight lines 12y = – (p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’.
Answer:
Slope of the first line 12y = -(p + 3)x + 12
y = \(-\frac{(p+3) x}{12}+1\) (comparing with y = mx + c)
Slope of the second line (m₁) = \(\frac{-(p+3)}{12}\)
Slope of the second line 12x – 7y = 16
(m₂) = \(\frac{-a}{b}=\frac{-12}{-7}=\frac{12}{7}\)
Since the two lines are perpemdicular.
m₁ × m₂ = -1
\(\frac{-(p+3)}{12} \times \frac{12}{7}=-1 \Rightarrow \frac{-(p+3)}{7}=-1\)
-(p + 3) = -7
– p – 3 = – 7 ⇒ -p = -7 + 3
– p = -4 ⇒ p = 4
The value of p = 4

Question 24.
Prove that 1 + \(\frac{\cot ^{2} \theta}{1+\csc \theta}\) = cosec θ
Answer:

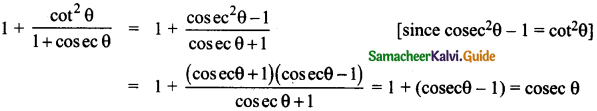
Question 25.
Find the standard deviation of first 21 natural numbers.
Answer:
Here n = 21
Standard deviation of the first ‘n’ natural numbers,
= \(\sqrt{\frac{n^{2}-1}{12}}\)
1,2,3,4, ……. , 21 = \(\sqrt{\frac{21^{2}-1}{12}}=\sqrt{\frac{441-1}{12}}=\sqrt{\frac{440}{12}}\)
= \(\sqrt{36.666}\) = \(\sqrt{36.67}\)
= 6.055 = 6.06
Standard deviation of first 21 natural numbers = 6.06

Question 26.
How many litres of water will a hemispherical tank hold whose diameter is 4.2m?
Answer:
Radius of the tank = \(\frac{4.2}{2}\) = 2.1 m
Volume of the hemisphere = \(\frac{2}{3}\) πr³ cu. unit
= \(\frac{2}{3} \times \frac{22}{7}\) × 2.1 × 2.1 × 2.1 m³
= 19.404 m³
= 19.4o4 × 1000 litre
= 19,4o4 litres

Question 27.
A two digit number is formed with the digits 2, 5, 9 (repetition is allowed). Find the probability that the number is divisible by 2.
Answer:
Sample space (S) = {22, 25, 29, 55, 59, 52, 99, 92, 95}
n(S) = 9
Let A be the event of getting number divisible by 2
A = {22,52,92}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{9}=\frac{1}{3}\)

Question 28.
Solve √x + 5 = 2x + 3 using formula method.
Answer:
\(\sqrt{x+5}\) = 2x + 3
\((\sqrt{x+5})^{2}\) = (2x + 3)²
x + 5 = 4x² + 9 + 12x
4x² + 11x + 4 = 0
Here a = 4, b = 11, c = 5
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
= \(\frac{-11 \pm \sqrt{121-64}}{8}\)
= \(\frac{-11 \pm \sqrt{57}}{8}\)
∴ x = \(\frac{-11+\sqrt{57}}{8}\) ; x = \(\frac{-11-\sqrt{57}}{8}\)

PART – III

III. Answer any ten questions. Question No. 42 is compulsory. [10 × 5 = 50]

Question 29.
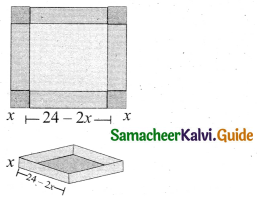
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the comers and turning up the sides as shown. Express the volume V of the box as a function of x.

Question 30.
Find the greatest number consisting of 6 digits which is exactly divisible by 24,15,36?

Question 31.
The present value of a machine is ₹40,000 and its value depreciates each year by 10%. Find the estimated value of the machine in the 6th year.

Question 32.
The sum of the digits of a three-digit number is 11. If the digits are reversed, the new number is 46 more than five times the old number. If the hundreds digit plus twice the tens digit is equal to the units digit, then find the original three digit number?

Question 33.
Find the square root of the expression \(\frac{4 x^{2}}{y^{2}}+\frac{20 x}{y}+13-\frac{30 y}{x}+\frac{9 y^{2}}{x^{2}}\)

Question 34.
If α, β are the roots of 7x² + ax + 2 = 0 and if β – α = \(\frac { -13 }{ 7 }\) . Find the values of a.

Question 35.
State and prove Angle Bisector Theorem.

Question 36.
A quadrilateral has vertices at A(-4, -2) , B(5, -1) , C(6, 5) and D(-7, 6). Show that the mid-points of its sides form a parallelogram.

Question 37.
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively.
If the distance between the ships is 200 \(\left(\frac{\sqrt{3}+1}{\sqrt{3}}\right)\) meters, find the height of the light house.

Question 38.
A shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.

Question 39.
Two dice are rolled together. Find the probability of getting a doublet or sum of faces as 4.

Question 40.
Given f(x) = x – 2 ; g(x) = 3x + 5; h(x) = 2x – 3 verify that (goh) of = go (hof)

Question 41.
A 20 m deep well with inner diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22m by 14m. Find the height of the platform.

Question 42.
The mean and standard deviation of 20 items are found to be 10 and 2 respectively. At the time of checking it was found that an item 12 was wrongly entered as 8. Calculate the correct mean and standard deviation.

PART – IV

IV. Answer all the questions. [2 × 8 = 16]

Question 43.
(a) Construct a triangle similar to a given triangle PQR with its sides equal to \(\frac { 7 }{ 3 }\) of the corresponding sides of the triangle PQR (scale factor \(\frac { 7 }{ 3 }\)).

[OR]

(b) Draw a circle of diameter 6 cm from a point P, which is 8 cm away from its centre. Draw the two tangents PA and PB to the circle and measure their lengths.

Question 44.
(a) Draw the graph of y = x² – 5x – 6 and hence solve x² – 5x – 14 = 0.

[OR]

(b) Solve graphically 2x² + x – 6 = 0.

Must Read:

INDHOTEL Pivot Point Calculator