Samacheer Kalvi 11th Business Maths Guide Chapter 1 Matrices and Determinants Ex 1.5

Students can download 11th Business Maths Chapter 1 Matrices and Determinants Ex 1.5 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 1 Matrices and Determinants Ex 1.5

Samacheer Kalvi 11th Business Maths Matrices and Determinants Ex 1.5 Text Book Back Questions and Answers

Choose the Correct Answer.

Question 1.
The value of x if \(\left|\begin{array}{lll}
0 & 1 & 0 \\
x & 2 & x \\
1 & 3 & x
\end{array}\right|=0\) is
(a) 0, -1
(b) 0, 1
(c) -1, 1
(d) -1, -1
Answer:
(b) 0, 1
Hint:
0 – 1[x² – x] + 0 = 0
⇒ x² – x = 0
⇒ x(x – 1) = 0
⇒ x = 0 (or) x = 1

Question 2.
The value of \(\left|\begin{array}{lll}
2 x+y & x & y \\
2 y+z & y & z \\
2 z+x & z & x
\end{array}\right|\) is
(a) xyz
(b) x + y + z
(c) 2x + 2y + 2z
(d) 0
Answer:
(d) 0
Hint:
= \(\left|\begin{array}{lll}
2 x & x & y \\
2 y & y & z \\
2 z & z & x
\end{array}\right|\) C₁ → C₁ – C₃
= 0 (C₁ and C₂ are proportional)

Question 3.
The cofactor of -7 in the determinant \(\left|\begin{array}{rrr}
2 & -3 & 5 \\
6 & 0 & 4 \\
1 & 5 & -7
\end{array}\right|\) is
(a) -18
(b) 18
(c) -7
(d) 7
Answer:
(b) 18
Hint:
A cofactor of -7 = \(\left|\begin{array}{rr}
2 & -3 \\
6 & 0
\end{array}\right|\)
= 0 + 18
= 18

Question 4.
If Δ = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 1 & 2 \\
2 & 3 & 1
\end{array}\right|\) then \(\left|\begin{array}{lll}
3 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right|\) is
(a) Δ
(b) -Δ
(c) 3Δ
(d) -3Δ
Answer:
(b) -Δ
Hint:
\(\left|\begin{array}{lll}
3 & 1 & 2 \\
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right|=-\left|\begin{array}{lll}
1 & 2 & 3 \\
3 & 1 & 2 \\
2 & 3 & 1
\end{array}\right|\) R₁ ↔ R₂
= -Δ

Question 5.
The value of the determinant \(\left|\begin{array}{lll}
a & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right|^{2}\) is
(a) abc
(b) 0
(c) a²b²c²
(d) -abc
Answer:
(c) a²b²c²
Hint:
\(a^{2} b^{2} c^{2}\left|\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
= a²b²c² × 1²
= a²b²c²

Question 6.
If A is square matrix of order 3 then |kA| is:
(a) k|A|
(b) -k|A|
(c) k³|A|
(d) -k³|A|
Answer:
(c) k³|A|

Question 7.
adj (AB) is equal to:
(a) adj A adj B
(b) adj A^T adj B^T
(c) adj B adj A
(d) adj B^T adj A^T
Answer:
(c) adj B adj A

Question 8.
The inverse matrix of \(\left(\begin{array}{cc}
\frac{4}{5} & \frac{5}{12} \\
\frac{2}{5} & \frac{1}{2}
\end{array}\right)\) is
(a) \(\frac{7}{30}\left(\begin{array}{cc}
\frac{1}{2} & \frac{5}{12} \\
\frac{2}{5} & \frac{4}{5}
\end{array}\right)\)
(b) \(\frac{7}{30}\left(\begin{array}{cc}
\frac{1}{2} & \frac{-5}{12} \\
\frac{-2}{5} & \frac{1}{5}
\end{array}\right)\)
(c) \(\frac{30}{7}\left(\begin{array}{rr}
\frac{1}{2} & \frac{5}{12} \\
\frac{2}{5} & \frac{4}{5}
\end{array}\right)\)
(d) \(\frac{30}{7}\left(\begin{array}{rr}
\frac{1}{2} & \frac{-5}{12} \\
\frac{-2}{5} & \frac{4}{5}
\end{array}\right)\)
Answer:
(c) \(\frac{30}{7}\left(\begin{array}{rr}
\frac{1}{2} & \frac{5}{12} \\
\frac{2}{5} & \frac{4}{5}
\end{array}\right)\)

Question 9.
If A = \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) such that ad – bc ≠ 0 then A^-1 is:
(a) \(\frac{1}{a d-b c}\left[\begin{array}{cc}
d & b \\
-c & a
\end{array}\right]\)
(b) \(\frac{1}{a d-b c}\left[\begin{array}{ll}
d & b \\
c & a
\end{array}\right]\)
(c) \(\frac{1}{a d-b c}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]\)
(d) \(\frac{1}{a d-b c}\left[\begin{array}{ll}
d & -b \\
c & a
\end{array}\right]\)
Answer:
(c) \(\frac{1}{a d-b c}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]\)
Hint:

Question 10.
The number of Hawkins-Simon conditions for the viability of input-output analysis is:
(a) 1
(b) 3
(c) 4
(d) 2
Answer:
(d) 2

Question 11.
The inventor of input-output analysis is:
(a) Sir Francis Galton
(b) Fisher
(c) Prof. Wassily W. Leontief
(d) Arthur Cayley
Answer:
(c) Prof. Wassily W. Leontief

Question 12.
Which of the following matrix has no inverse?
(a) \(\left(\begin{array}{rr}
-1 & 1 \\
1 & -4
\end{array}\right)\)
(b) \(\left(\begin{array}{rr}
2 & -1 \\
-4 & 2
\end{array}\right)\)
(c) \(\left(\begin{array}{cc}
\cos a & \sin a \\
-\sin a & \cos a
\end{array}\right)\)
(d) \(\left(\begin{array}{rr}
\sin a & \sin a \\
-\cos a & \cos a
\end{array}\right)\)
Answer:
(b) \(\left(\begin{array}{rr}
2 & -1 \\
-4 & 2
\end{array}\right)\)
Hint:
So \(\left(\begin{array}{rr}
2 & -1 \\
-4 & 2
\end{array}\right)\) has no inverse.

Question 13.
Inverse of \(\left(\begin{array}{ll}
3 & 1 \\
5 & 2
\end{array}\right)\) is:
(a) \(\left(\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right)\)
(b) \(\left(\begin{array}{rr}
-2 & 5 \\
1 & -3
\end{array}\right)\)
(c) \(\left(\begin{array}{rr}
3 & -1 \\
-5 & -3
\end{array}\right)\)
(d) \(\left(\begin{array}{rr}
-3 & 5 \\
1 & -2
\end{array}\right)\)
Answer:
(a) \(\left(\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right)\)
Hint:
Let A = \(\left(\begin{array}{ll}
3 & 1 \\
5 & 2
\end{array}\right)\)
|A| = [6 – 5] = 1
adj A = \(\left[\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right]\)
∴ A^-1 = \(\left[\begin{array}{rr}
2 & -1 \\
-5 & 3
\end{array}\right]\)

Question 14.
If A = \(\left(\begin{array}{rr}
-1 & 2 \\
1 & -4
\end{array}\right)\) then A (adj A) is:
(a) \(\left(\begin{array}{ll}
-4 & -2 \\
-1 & -1
\end{array}\right)\)
(b) \(\left(\begin{array}{rr}
4 & -2 \\
-1 & 1
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\)
(d) \(\left(\begin{array}{ll}
0 & 2 \\
2 & 0
\end{array}\right)\)
Answer:
(c) \(\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\)
Hint:
A = \(\left(\begin{array}{rr}
-1 & 2 \\
1 & -4
\end{array}\right)\)
|A| = 4 – 2 = 2
We know that A (adj A) = |A| I
⇒ 2 \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)=\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\)

Question 15.
If A and B non-singular matrix then, which of the following is incorrect?
(a) A² = I implies A^-1 = A
(b) I^-1 = I
(c) If AX = B then X = B^-1A
(d) If A is square matrix of order 3 then |adj A| = |A|²
Answer:
(c) If AX = B then X = B^-1A
Hint:
If AX = B then X = A^-1B so, X = B^-1A is incorrect.

Question 16.
The value of \(\left|\begin{array}{rrr}
5 & 5 & 5 \\
4 x & 4 y & 4 z \\
-3 x & -3 y & -3 z
\end{array}\right|\) is:
(a) 5
(b) 4
(c) 0
(d) -3
Answer:
(c) 0
Hint:
= 4 × (-3) \(\left|\begin{array}{lll}
5 & 5 & 5 \\
x & y & z \\
x & y & z
\end{array}\right|\)
[Take out 4 from R₂ and -3 from R₃]
= 0 (∵ R₂ ≡ R₃)

Question 17.
If A is an invertible matrix of order 2 then det (A^-1) be equal
(a) det (A)
(b) \(\frac{1}{{det}(A)}\)
(c) 1
(d) 0
Answer:
(b) \(\frac{1}{{det}(A)}\)
Hint:
AA^-1 = I
|AA^-1| = |I|
|A| |A^-1| = 1
|A^-1| = \(\frac{1}{|\mathrm{A}|}\)
det A^-1 = \(\frac{1}{\det (A)}\)

Question 18.
If A is 3 × 3 matrix and |A| = 4 then |A^-1| is equal to:
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{16}\)
(c) 2
(d) 4
Answer:
(a) \(\frac{1}{4}\)
Hint:
|A^-1| = \(\frac{1}{|A|}=\frac{1}{4}\)

Question 19.
If A is a square matrix of order 3 and |A| = 3 then |adj A| is equal to:
(a) 81
(b) 27
(c) 3
(d) 9
Answer:
(d) 9
Hint:
|adj A| = |A|² = 3² = 9

Question 20.
The value of \(\left|\begin{array}{ccc}
x & x^{2}-y z & 1 \\
y & y^{2}-z x & 1 \\
z & z^{2}-x y & 1
\end{array}\right|\) is:
(a) 1
(b) 0
(c) -1
(d) -xyz
Answer:
(b) 0
Hint:

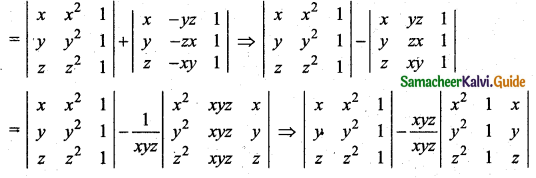
Question 21.
If A = \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\), then |2A| is equal to:
(a) 4 cos 2θ
(b) 4
(c) 2
(d) 1
Answer:
(b) 4
Hint:
|2A| = 2² |A|
= 4 \(\left|\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right|\)
= 4 [cos²θ + sin²θ]
= 4 × 1
= 4

Question 22.
If Δ = \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\) and A_ij is cofactor of a_ij, then value of Δ is given by:
(a) a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
(b) a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₁
(c) a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
(d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
Answer:
(d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

Question 23.
If \(\left|\begin{array}{ll}
x & 2 \\
8 & 5
\end{array}\right|=0\) then the value of x is:
(a) \(\frac{-5}{6}\)
(b) \(\frac{5}{6}\)
(c) \(\frac{-16}{5}\)
(d) \(\frac{16}{5}\)
Answer:
(d) \(\frac{16}{5}\)
Hint:
\(\left|\begin{array}{ll}
x & 2 \\
8 & 5
\end{array}\right|=0\)
5x – 16 = 0
⇒ x = \(\frac{16}{5}\)

Question 24.
If \(\left|\begin{array}{ll}
4 & 3 \\
3 & 1
\end{array}\right|\) = -5 then the value of \(\left|\begin{array}{rr}
20 & 15 \\
15 & 5
\end{array}\right|\) is:
(a) -5
(b) -125
(c) -25
(4) 0
Answer:
(b) -125
Hint:
\(\left|\begin{array}{rr}
20 & 15 \\
15 & 5
\end{array}\right|\)
= 5 × 5 \(\left|\begin{array}{ll}
4 & 3 \\
3 & 1
\end{array}\right|\)
= 5 × 5 × (-5)
= -125

Question 25.
If any three rows or columns of a determinant are identical then the value of the determinant is:
(a) 0
(b) 2
(c) 1
(d) 3
Answer:
(a) 0