Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 10 Operations Research Ex 10.1
Samacheer Kalvi 11th Business Maths Operations Research Ex 10.1 Text Book Back Questions and Answers
Question 1.
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹5 and ₹3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
Solution:
(i) Variables: Let x1 and x2 denotes the number of pens in type A and type B.
(ii) Objective function:
Profit on x1 pens in type A is = 5x1
Profit on x2 pens in type B is = 3x2
Total profit = 5x1 + 3x2
Let Z = 5x1 + 3x2, which is the objective function.
Since the B total profit is to be maximized, we have to maximize Z = 5x1 + 3x2
![]()
(iii) Constraints:
Raw materials required for each pen A is twice as that of pen B.
i.e., for pen A raw material required is 2x1 and for B is x2.
Raw material is sufficient only for 1000 pens per day
∴ 2x1 + x2 ≤ 1000
Pen A requires 400 clips per day
∴ x1 ≤ 400
Pen B requires 700 clips per day
∴ x2 ≤ 700
(iv) Non-negative restriction:
Since the number of pens is non-negative, we have x1 > 0, x2 > 0.
Thus, the mathematical formulation of the LPP is
Maximize Z = 5x1 + 3x2
Subj ect to the constrains
2x1 + x2 ≤ 1000, x1 ≤ 400, x2 ≤ 700, x1, x2 ≥ 0
![]()
Question 2.
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
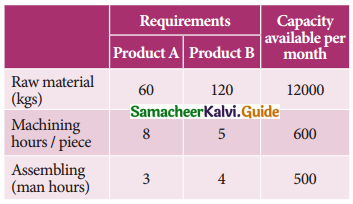
Formulate this problem as a linear programming problem to maximize the profit.
Solution:
(i) Variables: Let x1 and x2 denote the two types products A and B respectively.
(ii) Objective function:
Profit on x1 units of type A product = 30x1
Profit on x2 units of type B product = 40x2
Total profit = 30x1 + 40x2
Let Z = 30x1 + 40x2, which is the objective function.
Since the profit is to be maximized, we have to maximize Z = 30x1 + 40x2
![]()
(iii) Constraints:
60x1 + 120x2 ≤ 12,000
8x1 + 5x2 ≤ 600
3x1 + 4x2 ≤ 500
(iv) Non-negative constraints:
Since the number of products on type A and type B are non-negative, we have x1, x2 ≥ 0
Thus, the mathematical formulation of the LPP is
Maximize Z = 30x1 + 40x2
Subject to the constraints,
60x1 + 120x2 ≤ 12,000
8x1 + 5x2 ≤ 600
3x1 + 4x2 ≤ 500
x1, x2 ≥ 0
![]()
Question 3.
A company manufactures two models of voltage stabilizers viz., ordinary and autocut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at company’s own works. The assembly and testing time required for the two models are 0.8 hour each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
Solution:
(i) Variables : Let x1 and x2 denote the number of ordinary and auto-cut voltage stabilized.
(ii) Objective function:
Profit on x1 units of ordinary stabilizers = 100x1
Profit on x2 units of auto-cut stabilized = 150x2
Total profit = 100x1 + 150x2
Let Z = 100x1 + 150x2, which is the objective function.
Since the profit is to be maximized. We have to
Maximize, Z = 100x1 + 15x2
![]()
(iii) Constraints: The assembling and testing time required for x1 units of ordinary stabilizers = 0.8x1 and for x2 units of auto-cut stabilizers = 1.2x2
Since the manufacturing capacity is 720 hours per week. We get 0.8x1 + 1.2x2 ≤ 720
Maximum weekly sale of ordinary stabilizer is 600
i.e., x1 ≤ 600
Maximum weekly sales of auto-cut stabilizer is 400
i.e., x2 ≤ 400
(iv) Non-negative restrictions:
Since the number of both the types of stabilizer is non-negative, we get x1, x2 ≥ 0.
Thus, the mathematical formulation of the LPP is,
Maximize Z = 100x2 + 150x2
Subject to the constraints
0.8x1 + 1.2x2 ≤ 720, x1 ≤ 600, x2 ≤ 400, x1, x2 ≥ 0
![]()
Question 4.
Solve the following linear programming problems by graphical method.
(i) Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
(ii) Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
(iii) Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 > 6; x1+ 4x2 ≥ 12 and x1, x2 ≥ 0.
(iv) Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
(v) Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
(vi) Minimize Z = 20x1 + 40x2 subject to the constraints 36x1 + 6x2 ≥ 108; 3x1 + 12x2 ≥ 36; 20x1 + 10x2 ≥ 100 and x1, x2 ≥ 0.
Solution:
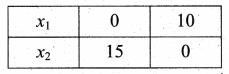
(i) Given that 30x1 + 20x2 ≤ 300
Let 30x1 + 20x2 = 300
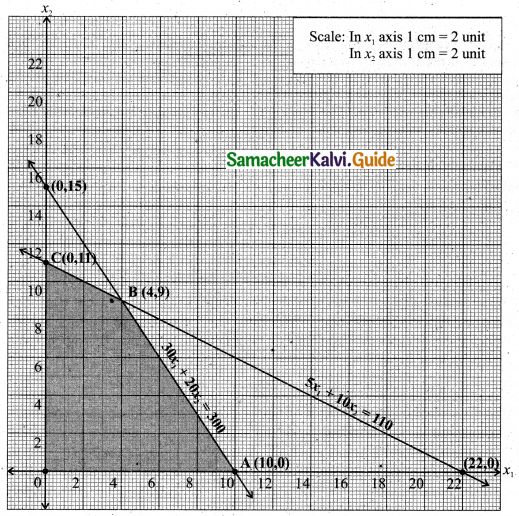
Therefore
3x1 + 2x2 = 30
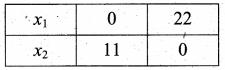
Also given that 5x1 + 10x2 ≤ 110
Let 5x1 + 10x2 = 110
x1 + 2x2 = 22
To get point of intersection, (i.e., the to get eo-ordinates of B)
3x1 + 2x2 = 30 …….(1)
x1 + 2x2 = 22 ……..(2)
(1) – (2) ⇒ 2x1 = 8
x1 = 4
x1 = 4 substitute in (1),
x1 + 2x2 = 22
4 + 2x2 = 22
2x2 = 18
x2 = 9
i.e., B is (4, 9)
The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the points are O(0, 0), A(10, 0), B(4, 9), C(0, 11).
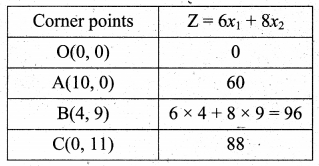
The maximum value of Z occurs at B.
∴ The optimal solution is x1 = 4, x2 = 9 and Zmax = 96
![]()
(ii) Given that 960x1 + 640x2 ≤ 15360
Let 960x1 + 640x2 = 15360
3x1 + 2x2 = 48

Also given that x1 + x2 ≤ 20
Let x1 + x2 = 20

To get point of intersection
3x1 + 2x2= 48 …..(1)
x1 + x2 = 20 ……(2)
(2) × -2 ⇒ -2x1 – 2x2 = -40 …..(3)
(1) + (3) ⇒ x1 = 8
x1 = 8 substitute in (2),
8 + x2 = 20
x2 = 12
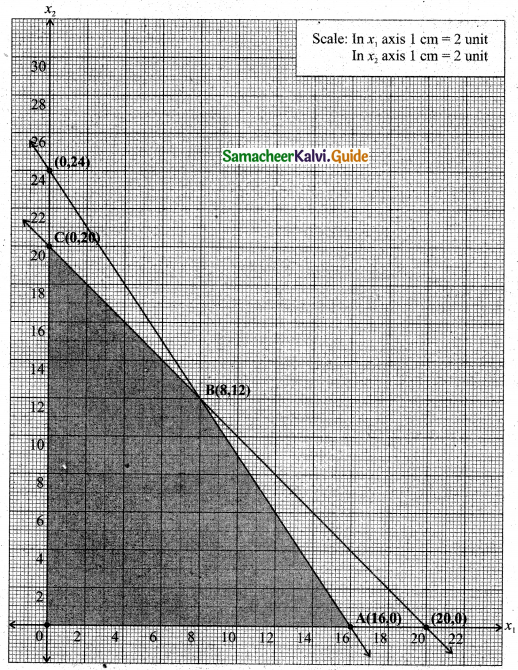
The feasible region satisfying all the given conditions is OABC.
The co-ordinates of the comer points are O(0, 0), A(16, 0), B(8,12) and C(0, 16).
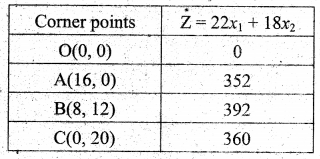
The maximum value of Z occurs at B(8, 12).
∴ The optimal solution is x1 = 8, x2 = 12 and Zmax = 392
![]()
(iii) Given that 5x1 + x2 ≥ 10
Let 5x1 + x2 = 10

Also given that x1 + x2 ≥ 6
Let x1 + x2 = 6
Also given that x1 + 4x2 ≥ 12
Let x1 + 4x2 = 12

To get C
5x1 + x2 = 10 ……..(1)
x1 + x2 = 6 ………(2)
(1) – (2) ⇒ 4x1 = 4
⇒ x1 = 1
x = 1 substitute in (2)
⇒ x1 + x2 = 6
⇒ 1 + x2 = 6
⇒ x2 = 5
∴ C is (1, 5)
To get B
x1 + x2 = 6
x1 + 4x2 = 12
(1) – (2) ⇒ -3x2 = -6
x2 = 2
x2 = 2 substitute in (1), x1 = 4
∴ B is (4, 2)
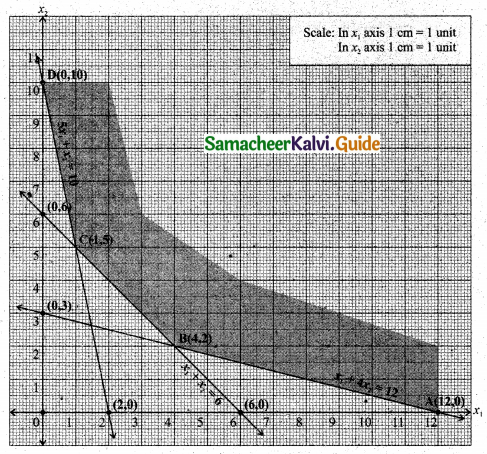
The feasible region satisfying all the conditions is ABCD.
The co-ordinates of the comer points are A(12, 0), B(4, 2), C(1, 5) and D(0, 10).

The minimum value of Z occours at C(1, 5).
∴ The optimal solution is x1 = 1, x2 = 5 and Zmin = 13
![]()
(iv) Given that 3x1 + x2 ≤ 9
Let 3x1 + x2 = 9
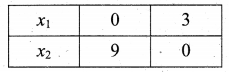
Also given that x1 + 2x2 ≤ 8
Let x1 + 2x2 = 8
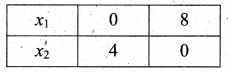
3x1 + x2 = 9 ………(1)
x1 + 2x2 = 8 ……..(2)
(1) × 2 ⇒ 6x1 + 2x2 = 18 ……..(3)
(2) + (3) ⇒ -5x1 = -10
x1 = 2
x1 = 2 substitute in (1)
3(2) + x2 = 9
x2 = 3
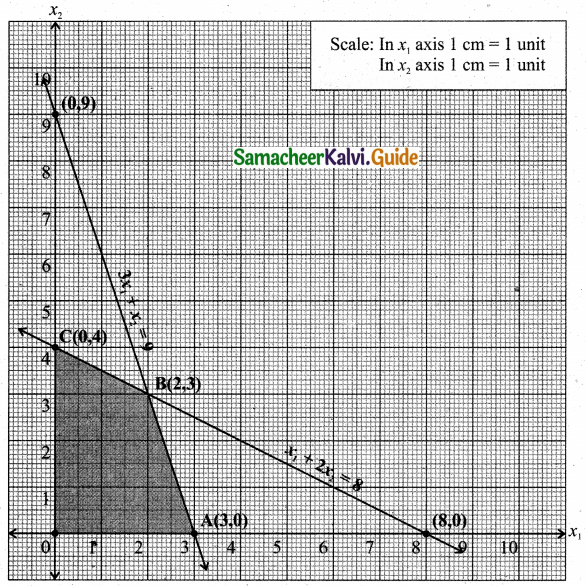
The feasible region satisfying all the conditions is OABC.
The co-ordinates of the corner points are O(0, 0), A(3, 0), B(2, 3), C(0, 4)
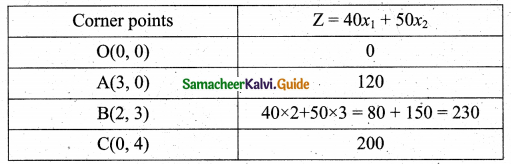
The maximum value of Z occurs at (2, 3).
∴ The optimal solution is x1 = 2, x2 = 3 and Zmax = 230
![]()
(v) Given that 3x1 + 3x2 ≤ 36
Let 3x1 + 3x2 = 36

Also given that 5x1 + 2x2 ≤ 50
Let 5x1 + 2x2 = 50
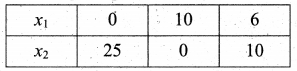
x1 + x2 = 12 ……(1)
5x1 + 2x2 = 50 ……….(2)
(1) × 2 ⇒ 2x1 + 2x2 = 24 ………(3)
(2) – (3) ⇒ 3x1 = 26
x1 = \(\frac{26}{3}\) = 8.66
put x1 = \(\frac{26}{3}\) substitute in (1)
x1 + x2 = 12
x2 = 12 – x1
x2 = 26 – \(\frac{26}{3}\) = \(\frac{10}{3}\) = 3.33
Also given that 2x1 + 6x2 ≤ 60
Let 2x1 + 6x2 = 60
x1 + 3x2 = 30

x1 + x2 = 12 …….(1)
x1 + 3x2 = 30 …….(2)
(1) – (2) ⇒ -2x2 = -18
x2 = 9
x2 = 9 substitute in (1) ⇒ x1 = 3
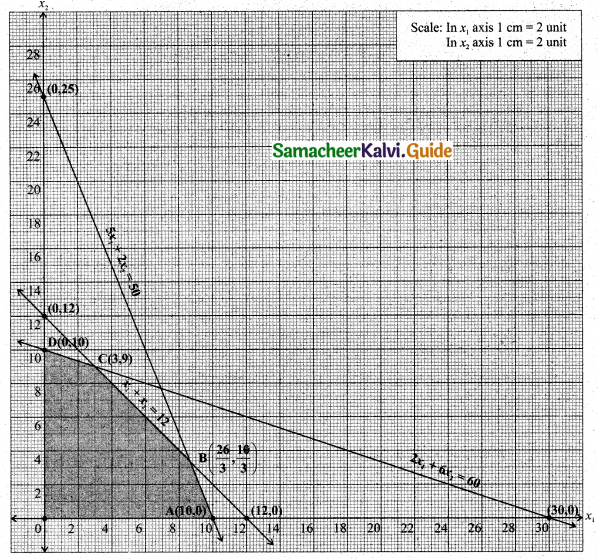
The feasible region satisfying all the given conditions is OABCD.
The co-ordinates of the comer points are O(0, 0), A(10, 0), B(\(\frac{26}{3}, \frac{10}{3}\)), and C = (3, 9) and D (0, 10)

The maximum value of Z occurs at C(3, 9)
∴ The optimal solution is x1 = 3, x2 = 9 and Zmax = 330
![]()
(vi) Given that 36x1 + 6x2 ≥ 108
Let 36x1 + 6x2 = 108
6x1 + x2 = 18

Also given that 3x1 + 12x2 ≥ 36
Let 3x1 + 12x2 = 36
x1 + 4x2 = 12
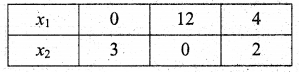
Also given that 20x1 + 10x2 ≥ 100
Let 20x1 + 10x2 = 100
2x1 + x2 = 10

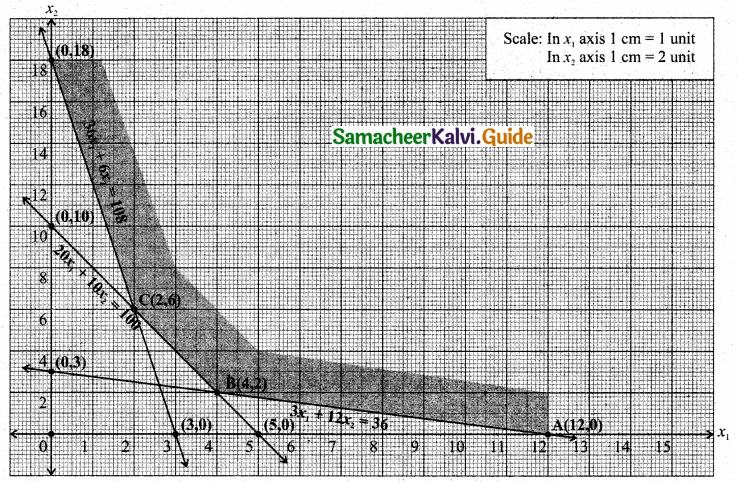
The feasible region satisfying all the conditions is ABCD.
The co-ordinates of the comer points are A(12, 0), B(4, 2), C(2, 6) and D(0, 18).
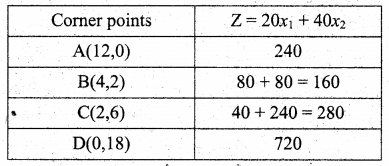
The minimum value of Z occurs at B(4, 2)
∴ The optimal solution is x1 = 4, x2 = 2 and Zmin = 160