Samacheer Kalvi 11th Business Maths Guide Chapter 10 Operations Research Ex 10.2

Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 10 Operations Research Ex 10.2

Samacheer Kalvi 11th Business Maths Operations Research Ex 10.2 Text Book Back Questions and Answers

Question 1.
Draw the network for the project whose activities with their relationships are given below:
Activities A, D, E can start simultaneously; B, C > A; G, F > D, C; H > E, F.
Solution:
Given: (i) A, D, E can start simultaneously.
(iii) A < B, C; C, D < G, F; E, F < H
Working rule:
A < B, C implies activity A is the immediate predecessor of activities B and C.
i.e., for activities B and C to occur, activity ‘A’ has to be completed.
Similarly for activities G, F to occur D and C has to completed for activity H to occur E and F has to be completed.
Step-1:

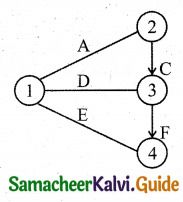
(∵ A, D and E are independents events)
Step-2:

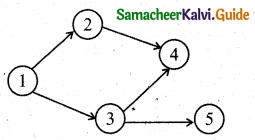
Note: Activities B, G and H are not a part of any activities immediate predecessor. So they have to merge into the lost node 5.

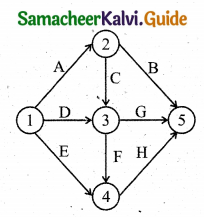
Question 2.
Draw the event oriented network for the following data:

Solution:
Step-1:

Step-2:

Step-3:

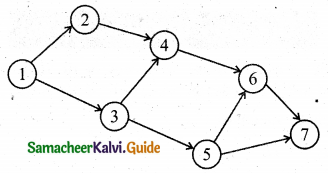
Question 3.
Construct the network for the projects consisting of various activities and their precedence relationships are as given below:
A, B, C can start simultaneously: A < F, E; B < D, C; E, D < G
Solution:
Step-1:

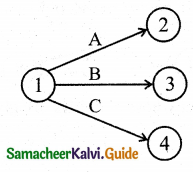
Step-2:

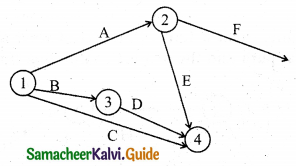
Step-3:

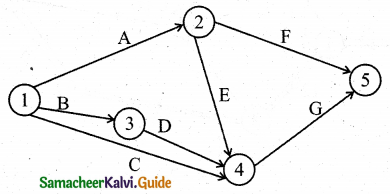
Question 4.
Construct the network for each the projects consisting of various activities and their precedence relationships are as given below:

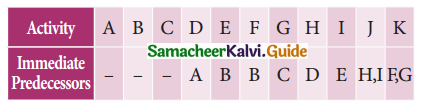
Solution:
Step-1:

Step-2:

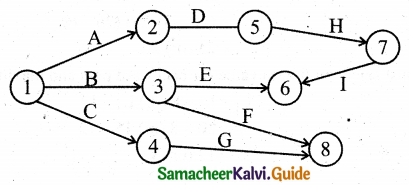
Step-3:

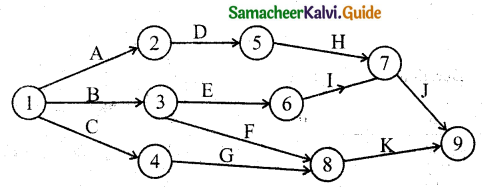
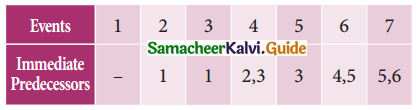
Question 5.
Construct the network for the project whose activities are given below.

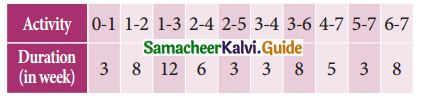
Calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity. Determine the critical path and the project completion time.
Solution:

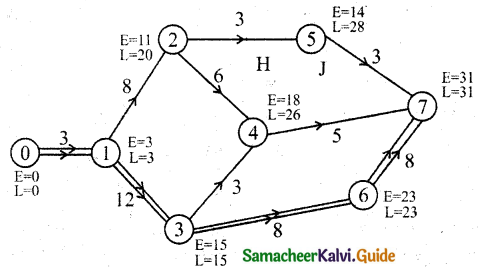
Forward pass:
E₁ = 0 + 3 = 3
E₂ = E₁ + t₁₂ = 8 + 3 = 11
E₃ = 3 + 12 = 15
E₄ = E₂ + 6 (or) E₃ + 3 = 11 + 6 (or) 15 + 3 = 18
[We must select a maximum value for forwarding pass]
E₄ = 15 + 3 = 18
E₂ = E₂ + 3 = 11 + 3 = 14
E₆ = E₃ + 8 = 15 + 8 = 23
E₇ = E₆ + 8 = 23 + 8 = 31
Backward pass:
L₇ = 31
L₆ = L₇ – 8 = 31 – 8 = 23
L₅ = L₇ – 3 = 31 – 3 = 28
L₄ = L₇ – 5 = 31 – 5 = 26
L₃ = L₆ – 8 = 23 – 8 = 15
L₂ = L₅ – 3 (or) L₄ – 6 = (28 – 3) (or) (26 – 6) = 25 (or) 20
[We must select a minimum value for a backward pass and maximum value for forwarding pass]
L₁ = L₂ – 8 (or) L₃ – 12 = 20 – 8 (or) 15 – 12 = 12 (or) 3 = 3
L₀ = 0

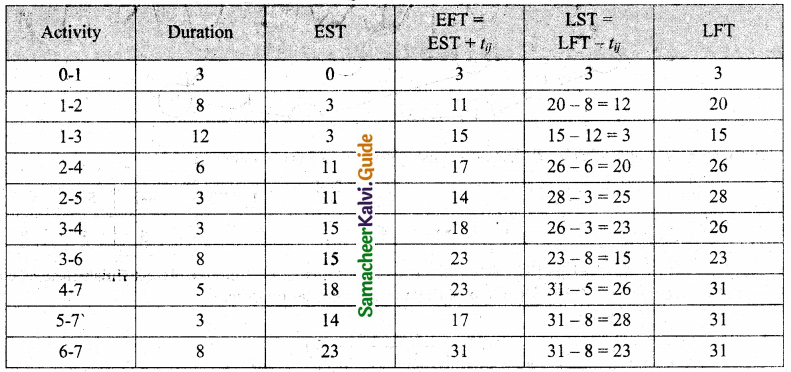
Critical path 0-1-3-6-7 and the duration is 31 works.

Question 6.
A project schedule has the following characteristics:

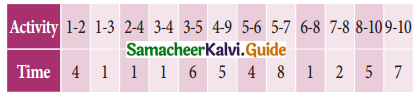
Construct the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
Solution:

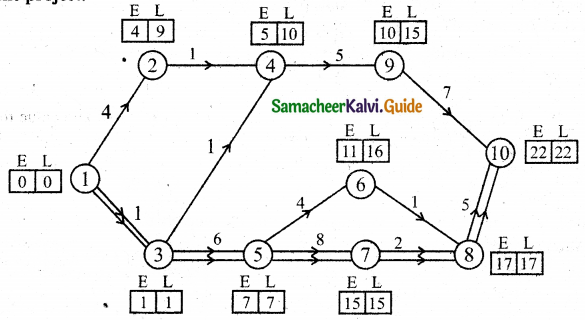
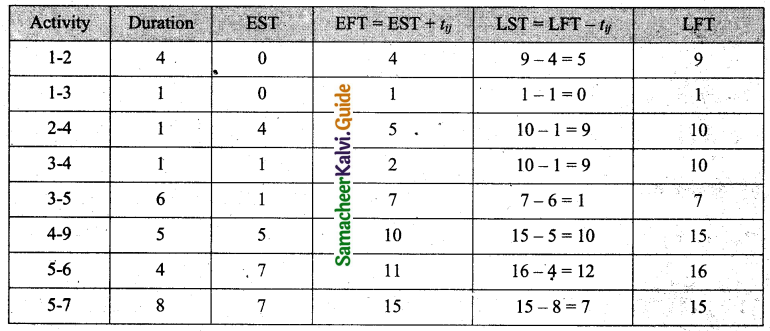
Forward pass:
E₁ = 0
E₂ = 0 + 4 = 4
E₃ = 0 + 1 = 1
E₄ = (E₂ + 1) (or) (E₃ + 1) = (4 + 1) (or) (1 + 1) = 5 (or) 2
[whichever is maximum we must select forward pass]
∴ E₄ = 5
E₅ = 1 + 6 = 7
E₆ = 7 + 4 = 11
E₇ = 8 + 7 = 15
E₈ = (E₇ + 2) (or) (E₆ + 1)
= (15 + 2) or (11 + 1)
= 17 or 12 [whichever is maximum]
∴ E₈ = 17
E₉ = 5 + 5 = 10
E₁₀ = (E₉ + 7) (or) (E₈ + 5)
= (10 + 7) (or) (17 + 5)
= 17 (or) 22 [Which is maximum]
E₁₀ = 22
Backward pass:
L₁₀ = 22
L₉ = 22 – 7 = 15
L₈ = 22 – 5 = 17
L₇ = 17 – 2 = 15
L₆ = 17 – 1 = 16
L₅ = (16 – 4) (or) (15 – 8) [whichever is minimum]
L₅ = 7
L₄ = 15 – 5 = 10
L₃ = (10 – 1) (or) (7 – 6) [whichever is minimum]
L₃ = 1
L₂ = 10 – 1 = 9
L₁ = 0
We can also find the critical path by this method, which also helps us to counter check the solution obtained by the table method.

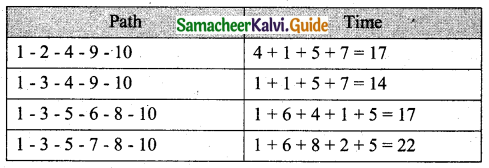
So critical path is 1-3-5-7-8-10 as it takes 22 units to complete the project.

Question 7.
Draw the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.

Solution:

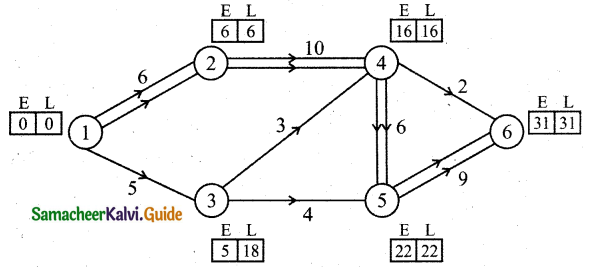
Forward pass:
E₁ = 0
E₂ = 0 + 6 = 6
E₃ = 0 + 5 = 5
E₄ = 6 + 10 = 16
E₅ = (E₄ + 6) (or) (E₃ + 4)
E₅ = (16 + 6) (or) (5 + 4) [whichever is maximum]
E₅ = 22
E₆ = (E₅ + 9)(or) (E₄ + 2)
E₆ = (22 + 9) (or) (4 + 2) [whichever is maximum]
E₆ = 31
Backward pass:
L₆ = 31
L₅ = 31 – 9 = 22
L₄ = 22 – 6 (or) 31 – 2 [whichever is minimum]
L₄ = 16
L₃ = 22 – 4 = 18
L₂ = 16 – 10 = 6
L₁ = 6 – 6 = 0


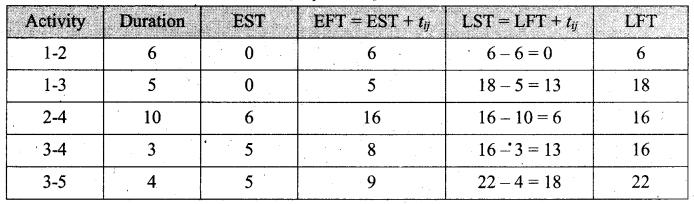
∴ EFT and LFT are the same on 1-2, 2-4, 4-5, 5-6, the vertical path is 1-2-4-5-6 and duration is 31 days to complete.

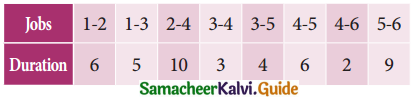
Question 8.
The following table gives the activities of a project and their duration in days.

Construct the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the critical path of the project and duration to complete the project.
Solution:

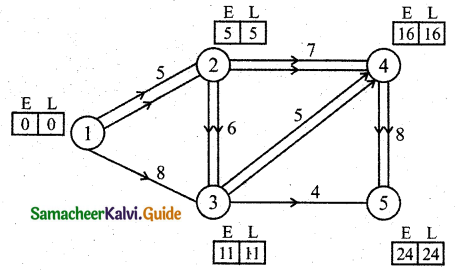
Forward pass:
E₁ = 0
E₂ = 0 + 5 = 5
E₃ = (0 + 8) (or) (5 + 6) [whichever is maximum]
E₃ = 11
E₄ = (11 + 5) (or) (5 + 7) [whichever is maximum]
E₄ = 16
E₅ = (11 + 4) (or) (16 + 8) [whichever is maximum]
E₅ = 24
Backward pass:
L₅ = 24
L₄ = 24 – 8 = 16
L₃ = (24 – 4) (or) (16 – 5) [whichever is minimum]
L₃ = 11
L₂ = (11 – 6) (or) (16 – 7) [whichever is minimum]
L₂ = 5
L₁ = (5 – 5) (or) (11 – 8) = 0 [whichever is minimum]


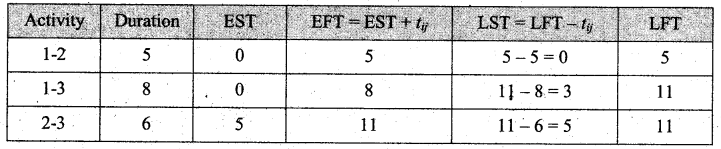
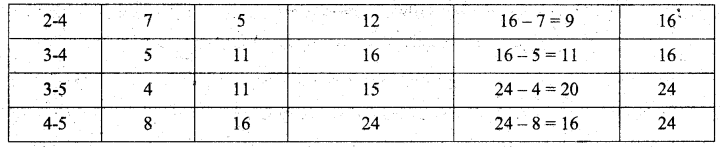
EFT and LFT are the same on 1-2, 2-3, 3-4, and 4-5
So critical path is 1-2-3-4-5 and the time taken is 24 days.

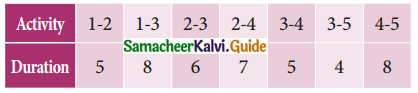
Question 9.
A project has the following time schedule

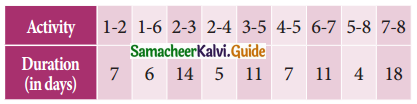
Construct the network and calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity and determine the critical path of the project and duration to complete the project.
Solution:

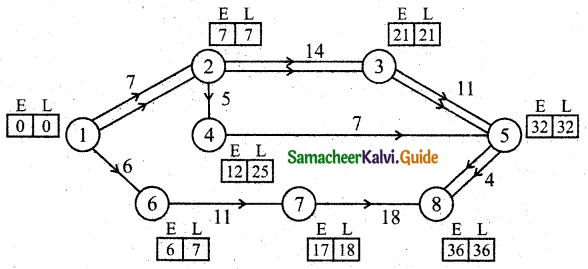
Forward pass:
E₁ = 0
E₂ = 0 + 7 = 7
E₃ = 7 + 14 = 21
E₄ = 7 + 5 = 12
E₅ = (21 + 11) (or) (2 + 7) = 32 [whichever is maximum]
E₆ = 0 + 6 = 6
E₇ = 6 + 11 = 17
E₈ = 32 + 4 = 36
Backward pass:
L₈ = 36
L₇ = 36 – 18 = 18
L₆ = 18 – 11 = 7
L₅ = 35 – 4 = 31
L₄ = 32 – 7 = 25
L₃ = 32 – 11 = 21
L₂ = (21 – 14) (or) (25 – 5) [whichever is minimum]
L₂ = 7
L₁ = 7 – 7 = 0

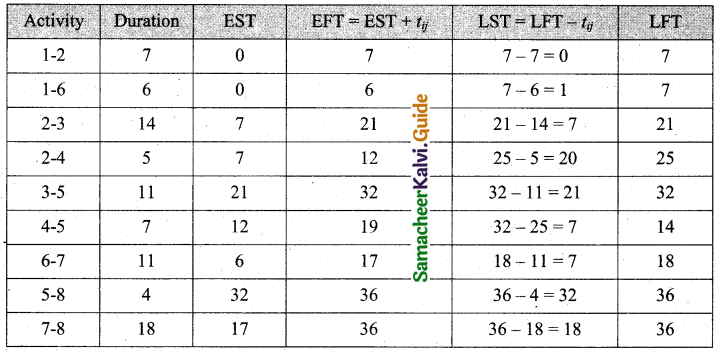
EFT and LFT are same is 1-2, 2-3, 3-5, 5-8.
Hence the critical path is 1-2-3-5-8 and the time to complete is 36 days.

Question 10.
The following table uses the activities in construction projects and relevant information.

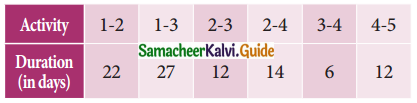
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time, and latest finish time of each activity, and find the critical path. Compute the project duration.
Solution:

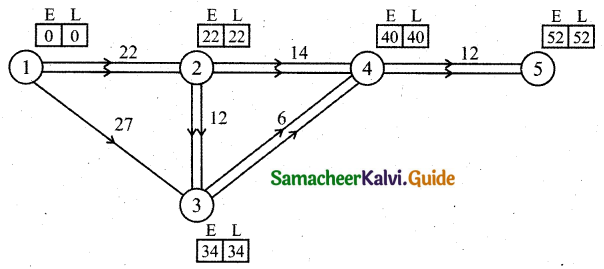
Forward pass:
E₁ = 0
E₂ = 0 + 22 = 22
E₃ = (0 + 27) (or) (22 + 12) = 34 [Maximum of both]
E₄ = (22 + 14) (or) (34 + 16) = 40
E₅ = 40 + 12 = 52
Backward pass:
L₅ = 32
L₄ = 52 – 12 = 40
L₃ = 40 – 6 = 34
L₂ = (40 – 14) (or) (34 – 12) = 22 [Minimum of both]
L₁ = 22 – 22 = 0

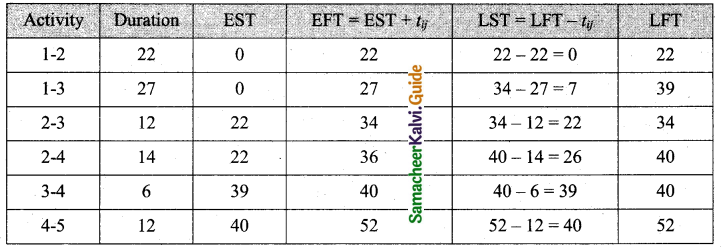
EFT and LFT are the same for 1-2, 2-3, 3-4, and 4-5.
So critical path is 1-2-3-4-5 time to complete is 52 days.