Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.3 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.3
Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.3 Text Book Back Questions and Answers
Question 1.
If the equation ax2 + 5xy – 6y2 + 12x + 5y + c = 0 represents a pair of perpendicular straight lines, find a and c.
Solution:
Comparing ax2 + 5xy – 6y2 + 12x + 5y + c = 0 with ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
We get a = a, 2h = 5, (or) h = \(\frac{5}{2}\), b = -6, 2g = 12 (or) g = 6, 2f = 5 (or) f = \(\frac{5}{2}\), c = c
Condition for pair of straight lines to be perpendicular is a + b = 0
a + (-6) = 0
a = 6
Next to find c. Condition for the given equation to represent a pair of straight lines is

R1 → R1 – R3
Expanding along first row we get 0 – 0 + (6 – c) [\(\frac{25}{4}\) + 36] = 0
(6-c) [\(\frac{25}{4}\) + 36] = 0
6 – c = 0
6 = c (or) c = 6
![]()
Question 2.
Show that the equation 12x2 – 10xy + 2y2 + 14x – 5y + 2 = 0 represents a pair of straight lines and also find the separate equations of the straight lines.
Solution:
Comparing 12x2 – 10xy + 2y2 + 14x – 5y + 2 = 0 with ax2 + 2hxy + by2 + 2gh + 2fy + c = 0
We get a = 12, 2h = -10, (or) h = -5, b = 2, 2g = 14 (or) g = 7, 2f = -5 (or) f = \(-\frac{5}{2}\), c = 2
Condition for the given equation to represent a pair of straight lines is \(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=0\)
\(\left|\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right|=\left|\begin{array}{rrr}
12 & -5 & 7 \\
-5 & 2 & \frac{-5}{2} \\
7 & \frac{-5}{2} & 2
\end{array}\right|\)
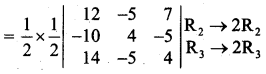
= \(\frac{1}{4}\) [12(16 – 25) + 5(-40 + 70) + 7(50 – 56)]
= \(\frac{1}{4}\) [12(-9) + 5(30) + 7(-6)]
= \(\frac{1}{4}\) [-108 + 150 – 42]
= \(\frac{1}{4}\) [0]
= 0
∴ The given equation represents a pair of straight lines.
Consider 12x2 – 10xy + 2y2 = 2[6x2 – 5xy + y2] = 2[(3x – y)(2x – y)] = (6x – 2y)(2x – y)
Let the separate equations be 6x – 2y + l = 0, 2x – y + m = 0
To find l, m
Let 12x2 – 10xy + 2y2 + 14x – 5y + 2 = (6x – 2y + l) (2x – y + m) ……. (1)
Equating coefficient of y on both sides of (1) we get
2l + 6m = 14 (or) l + 3m = 7 ………… (2)
Equating coefficient of x on both sides of (1) we get
-l – 2m = -5 ……… (3)
(2) + (3) ⇒ m = 2
Using m = 2 in (2) we get
l + 3(2) = 7
l = 7 – 6
l = 1
∴ The separate equations are 6x – 2y + 1 = 0, 2x – y + 2 = 0.
![]()
Question 3.
Show that the pair of straight lines 4x2 + 12xy + 9y2 – 6x – 9y + 2 = 0 represents two parallel straight lines and also find the separate equations of the straight lines.
Solution:
The given equation is 4x2 + 12xy + 9y2 – 6x – 9y + 2 = 0
Here a = 4, 2h = 12, (or) h = 6 and b = 9
h2 – ab = 62 – 4 × 9 = 36 – 36 = 0
∴ The given equation represents a pair of parallel straight lines
Consider 4x2 + 12xy + 9y2 = (2x)2 + 12xy + (3y)2
= (2x)2 + 2(2x)(3y) + (3y)2
= (2x + 3y)2
Here we have repeated factors.
Now consider, 4x2 + 12xy + 9y2 – 6x – 9y + 2 = 0
(2x + 3y)2 – 3(2x + 3y) + 2 = 0
t2 – 3t + 2 = 0 where t = 2x + 3y
(t – 1)(t – 2) = 0
(2x + 3y – 1) (2x + 3y – 2) = 0
∴ Separate equations are 2x + 3y – 1 = 0, 2x + 3y – 2 = 0
![]()
Question 4.
Find the angle between the pair of straight lines 3x2 – 5xy – 2y2 + 17x + y + 10 = 0.
Solution:
The given equation is 3x2 – 5xy – 2y2 + 17x + y + 10 = 0
Here a = 3, 2h = -5, b = -2
If θ is the angle between the given straight lines then
