Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.4 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.4
Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.4 Text Book Back Questions and Answers
Question 1.
Find the equation of the following circles having
(i) the centre (3, 5) and radius 5 units.
(ii) the centre (0, 0) and radius 2 units.
Solution:
(i) Equation of the circle is (x – h)2 + (y – k)2 = r2
Centre (h, k) = (3, 5) and radius r = 5
∴ Equation of the circle is (x – 3)2 + (y – 5)2 = 52
⇒ x2 – 6x + 9 + y2 – 10y + 25 = 25
⇒ x2 + y2 – 6x – 10y + 9 = 0
(ii) Equation of the circle when centre origin (0, 0) and radius r is x2 + y2 = r2
⇒ x2 + y2 = 22
⇒ x2 + y2 = 4
⇒ x2 + y2 – 4 = 0
Question 2.
Find the centre and radius of the circle
(i) x2 + y2 = 16
(ii) x2 + y2 – 22x – 4y + 25 = 0
(iii) 5x2 + 5y2+ 4x – 8y – 16 = 0
(iv) (x + 2) (x – 5) + (y – 2) (y – 1) = 0
Solution:
(i) x2 + y2 = 16
⇒ x2 + y2 = 42
This is a circle whose centre is origin (0, 0), radius 4.
(ii) Comparing x2 + y2 – 22x – 4y + 25 = 0 with general equation of circle x2 + y2 + 2gx + 2fy + c = 0
We get 2g = -22, 2f = -4, c = 25
g = -11, f = -2, c = 25
Centre = (-g, -f) = (11, 2)
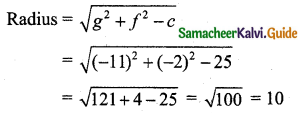
(iii) 5x2 + 5y2 + 4x – 8y – 16 = 0
To make coefficient of x2 unity, divide the equation by 5 we get,
\(x^{2}+y^{2}+\frac{4}{5} x-\frac{8}{5} y-\frac{16}{5}=0\)
Comparing the above equation with x2 + y2 + 2gx + 2fy + c = 0 we get,
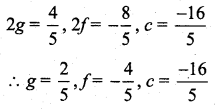
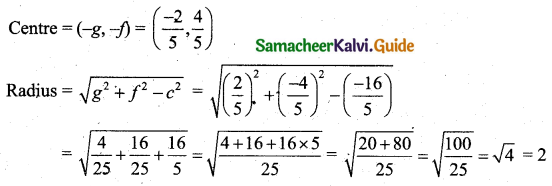
(iv) Equation of the circle is (x + 2) (x – 5) + (y – 2) (y – 1) = 0
x2 – 3x – 10 + y2 – 3y + 2 = 0
x2 + y2 – 3x – 3y – 8 = 0
Comparing this with x2 + y2 + 2gx + 2fy + c = 0
We get 2g = -3, 2f = -3, c = -8
g = \(\frac{-3}{2}\), f = \(\frac{-3}{2}\), c = -8
Centre (-g, -f) = \(\left(\frac{3}{2}, \frac{3}{2}\right)\)
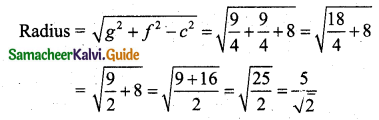
![]()
Question 3.
Find the equation of the circle whose centre is (-3, -2) and having circumference 16π.
Solution:
Circumference, 2πr = 16π
⇒ 2r = 16
⇒ r = 8
Equation of the circle when centre and radius are known is (x – h)2 + (y – k)2 = r2
⇒ (x + 3)2 + (y + 2)2 = 82
⇒ x2 + 6x + 9 + y2 + 4y + 4 = 64
⇒ x2 + y2 + 6x + 4y + 13 = 64
⇒ x2 + y2 + 6x + 4y – 51 = 0
Question 4.
Find the equation of the circle whose centre is (2, 3) and which passes through (1, 4).
Solution:
Centre (h, k) = (2, 3)
Equation of the circle with centre (h, k) and radius r is (x – h)2 + (y – k)2 = r2
⇒ (x – 2)2 + (y – 3)2 = (√2)2
⇒ x2 – 4x + 4 + y2 – 6y + 9 = 2
⇒ x2 + y2 – 4x – 6y + 11 = 0
![]()
Question 5.
Find the equation of the circle passing through the points (0, 1), (4, 3) and (1, -1).
Solution:
Let the required of the circle be x2 + y2 + 2gx + 2fy + c = 0 ……… (1)
It passes through (0, 1)
0 + 1 + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 …….. (2)
Again the circle (1) passes through (4, 3)
42 + 32 + 2g(4) + 2f(3) + c = 0
16 + 9 + 8g + 6f + c = 0
8g + 6f + c = -25 …….. (3)
Again the circle (1) passes through (1, -1)
12 + (-1)2 + 2g(1) + 2f(-1) + c = 0
1 + 1 + 2g – 2f + c = 0
2g – 2f + c = -2 ……… (4)
8g + 6f + c = -25
(4) × 4 subtracting we get, 8g – 8f + 4c = -8
14f – 3c = -17 ………. (5)
14f – 3c = -17
(2) × 3 ⇒ 6f + 3c = -3
Adding we get 20f = -20
f = -1
Using f = -1 in (2) we get, 2(-1) + c = -1
c = -1 + 2
c = 1
Using f = -1, c = 1 in (3) we get
8g + 6(-1)+1 = -25
8g – 6 + 1 = -25
8g – 5 = -25
8g = -20
g = \(\frac{-20}{8}=\frac{-5}{2}\)
using g = \(\frac{-5}{2}\), f = -1, c = 1 in (1) we get the equation of the circle.
x2 + y2 + 2(\(\frac{-5}{2}\))x + 2(-1)y + 1 = 0
x2 + y2 – 5x – 2y + 1 = 0
Question 6.
Find the equation of the circle on the line joining the points (1, 0), (0, 1), and having its centre on the line x + y = 1.
Solution:
Let the equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 ……… (1)
The circle passes through (1, 0)
12 + 02 + 2g(1) + 2f(0) + c = 0
1 + 2g + c = 0
2g + c = 1 …….. (2)
Again the circle (1) passes through (0, 1)
02 + 12 + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 ……. (3)
(2) – (3) gives 2g – 2f = 0 (or) g – f = 0 ………. (4)
Given that the centre of the circle (-g, -f) lies on the line x + y = 1
-g – f = 1 …….. (5)
(4) + (5) gives -2f = 1 ⇒ f = \(-\frac{1}{2}\)
Using f = \(-\frac{1}{2}\) in (5) we get
-g – (\(-\frac{1}{2}\)) = 1
-g = 1 – \(-\frac{1}{2}\) = \(\frac{1}{2}\)
g = \(-\frac{1}{2}\)
Using g = \(-\frac{1}{2}\) in (2) we get
2(\(-\frac{1}{2}\)) + c = -1
-1 + c = -1
c = 0
using g = \(-\frac{1}{2}\), f = \(-\frac{1}{2}\), c = 0 in (1) we get the equation of the circle,
x2 + y2 + 2(\(-\frac{1}{2}\))x + 2(\(-\frac{1}{2}\))y + 0 = 0
x2 + y2 – x – y = 0
![]()
Question 7.
If the lines x + y = 6 and x + 2y = 4 are diameters of the circle, and the circle passes through the point (2, 6) then find its equation.
Solution:
To get coordinates of centre we should solve the equations of the diameters x + y = 6, x + 2y = 4.
x + y = 6 ……. (1)
x + 2y = 4 ………. (2)
(1) – (2) ⇒ -y = 2
y = -2
Using y = -2 in (1) we get x – 2 = 6
x = 8
Centre is (8, -2) the circle passes through the point (2, 6).
Equation of the circle with centre (h, k) and radius r is (x – h)2 + (y – k)2 = r2
⇒ (x – 8)2 + (y + 2)2 = 102
⇒ x2 + y2 – 16x + 4y + 64 + 4 = 100
⇒ x2 + y2 – 16x + 4y – 32 = 0
Question 8.
Find the equation of the circle having (4, 7) and (-2, 5) as the extremities of a diameter.
Solution:
The equation of the circle when entremities (x1, y1) and (x2, y2) are given is (x – x1) (x – x2) + (y – y1) (y – y2) = 0
⇒ (x – 4) (x + 2) + (y – 7) (y – 5) = 0
⇒ x2 – 2x – 8 + y2 – 12y + 35 = 0
⇒ x2 + y2 – 2x – 12y + 27 = 0
![]()
Question 9.
Find the Cartesian equation of the circle whose parametric equations are x = 3 cos θ, y = 3 sin θ, 0 ≤ θ ≤ 2π.
Solution:
Given x = 3 cos θ, y = 3 sin θ
Now x2 + y2 = 9 cos2θ + 9 sin2θ
x2 + y2 = 9 (cos2θ + sin2θ)
x2 + y2 = 9 which is the Cartesian equation of the required circle.