Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.7 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.7
Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.7 Text Book Back Questions and Answers
Question 1.
If m1 and m2 are the slopes of the pair of lines given by ax2 + 2hxy + by2 = 0, then the value of m1 + m2 is:
(a) \(\frac{2 h}{b}\)
(b) \(-\frac{2 h}{b}\)
(c) \(\frac{2 h}{a}\)
(d) \(-\frac{2 h}{a}\)
Answer:
(b) \(-\frac{2 h}{b}\)
Question 2.
The angle between the pair of straight lines x2 – 7xy + 4y2 = 0 is:
(a) \(\tan ^{-1}\left(\frac{1}{3}\right)\)
(b) \(\tan ^{-1}\left(\frac{1}{2}\right)\)
(c) \(\tan ^{-1}\left(\frac{\sqrt{33}}{5}\right)\)
(d) \(\tan ^{-1}\left(\frac{5}{\sqrt{33}}\right)\)
Answer:
(c) \(\tan ^{-1}\left(\frac{\sqrt{33}}{5}\right)\)
Hint:
x2 – 7xy + 4y2 = 0
Here 2h = -7, a = 1, b = 4
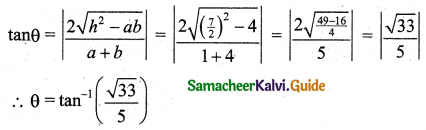
![]()
Question 3.
If the lines 2x – 3y – 5 = 0 and 3x – 4y – 7 = 0 are the diameters of a circle, then its centre is:
(a) (-1, 1)
(b) (1, 1)
(c) ( 1, -1)
(d) (-1, -1)
Answer:
(c) ( 1, -1)
Hint:
To get centre we must solve the given equations
2x – 3y – 5 = 0 …….(1)
3x – 4y – 7 = 0 ………(2)
(1) × 3 ⇒ 6x – 9y = 15
(2) × 2 ⇒ 6x – 8y = 14
Subtracting, -y = 1 ⇒ y = -1
Using y = -1 in (1) we get
2x + 3 – 5 = 0
⇒ 2x = 2
⇒ x = 1
Question 4.
The x-intercept of the straight line 3x + 2y – 1 = 0 is
(a) 3
(b) 2
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{3}\)
Hint:
To get x-intercept put y = 0 in 3x + 2y – 1 = 0 we get
3x – 1 = 0
x = \(\frac{1}{3}\)
![]()
Question 5.
The slope of the line 7x + 5y – 8 = 0 is:
(a) \(\frac{7}{5}\)
(b) \(-\frac{7}{5}\)
(c) \(\frac{5}{7}\)
(d) \(-\frac{5}{7}\)
Answer:
(b) \(-\frac{7}{5}\)
Hint:
Slope of 7x + 5y – 8 = 0 is = \(\frac{-x \text { coefficient }}{y \text { coefficient }}\) = \(-\frac{7}{5}\)
Question 6.
The locus of the point P which moves such that P is at equidistance from their coordinate axes is:
(a) y = \(\frac{1}{x}\)
(b) y = -x
(c) y = x
(d) y = \(\frac{-1}{x}\)
Answer:
(c) y = x
Hint:
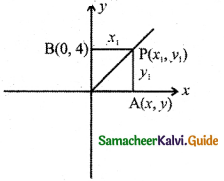
Given PA = PB
y1 = x1
∴ Locus is y = x
![]()
Question 7.
The locus of the point P which moves such that P is always at equidistance from the line x + 2y + 7 = 0:
(a) x + 2y + 2 = 0
(b) x – 2y + 1 = 0
(c) 2x – y + 2 = 0
(d) 3x + y + 1 = 0
Answer:
(a) x + 2y + 2 = 0
Hint:
Locus is line parallel to line x + 2y + 7 = 0 which is x + 2y + 2 = 0
Question 8.
If kx2 + 3xy – 2y2 = 0 represent a pair of lines which are perpendicular then k is equal to:
(a) \(\frac{1}{2}\)
(b) \(-\frac{1}{2}\)
(c) 2
(d) -2
Answer:
(c) 2
Hint:
Here a = k, b = -2
Condition for perpendicular is
a + b = 0
⇒ k – 2 = 0
⇒ k = 2
![]()
Question 9.
(1, -2) is the centre of the circle x2 + y2 + ax + by – 4 = 0, then its radius:
(a) 3
(b) 2
(c) 4
(d) 1
Answer:
(a) 3
Hint:
Given centre (-g, -f) = (1, -2)
From the given equation c = -4
Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-(-4)}=\sqrt{9}\) = 3
Question 10.
The length of the tangent from (4, 5) to the circle x2 + y2 = 16 is:
(a) 4
(b) 5
(c) 16
(d) 25
Answer:
(b) 5
Hint:
Length of the tangent from (x1, y1) to the circle x2 + y2 = 16 is \(\sqrt{x_{1}^{2}+y_{1}^{2}-16}=5\)
![]()
Question 11.
The focus of the parabola x2 = 16y is:
(a) (4 , 0)
(b) (-4, 0)
(c) (0, 4)
(d) (0, -4)
Answer:
(c) (0, 4)
Hint:
x2 = 16y
Here 4a = 16 ⇒ a = 4
Focus is (0, a) = (0, 4)
Question 12.
Length of the latus rectum of the parabola y2 = -25x:
(a) 25
(b) -5
(c) 5
(d) -25
Answer:
(a) 25
Hint:
y2 = -25a
Here 4a = 25 which is the length of the latus rectum.
![]()
Question 13.
The centre of the circle x2 + y2 – 2x + 2y – 9 = 0 is:
(a) (1, 1)
(b) (-1, 1)
(c) (-1, 1)
(d) (1, -1)
Answer:
(d) (1, -1)
Hint:
2g = -2, 2f = 2
g = -1, f = 1
Centre = (-g, -f) = (1, -1)
Question 14.
The equation of the circle with centre on the x axis and passing through the origin is:
(a) x2 – 2ax + y2 = 0
(b) y2 – 2ay + x2 = 0
(c) x2 + y2 = a2
(d) x2 – 2ay + y2 = 0
Answer:
(a) x2 – 2ax + y2 = 0
Hint:
Let the centre on the x-axis as (a, 0).
This circle passing through the origin so the radius
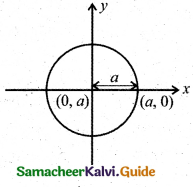
Now centre (h, k) = (a, 0)
Radius = a
Equation of the circle is (x – a)2 + (y – 0)2 = a2
⇒ x2 – 2ax + a2 + y2 = a2
⇒ x2 – 2ax + y2 = 0
![]()
Question 15.
If the centre of the circle is (-a, -b) and radius is \(\sqrt{a^{2}-b^{2}}\) then the equation of circle is:
(a) x2 + y2 + 2ax + 2by + 2b2 = 0
(b) x2 + y2 + 2ax + 2by – 2b2 = 0
(c) x2 + y2 – 2ax – 2by – 2b2 = 0
(d) x2 + y2 – 2ax – 2by + 2b2 = 0
Answer:
(a) x2 + y2 + 2ax + 2by + 2b2 = 0
Hint:
Equation of the circle is (x – h)2 + (y – k)2 = r2
⇒ (x + a)2 + (y + b)2 = a2 – b2
⇒ x2 + y2 + 2ax + 2by + a2 + b2 = a2 – b2
⇒ x2 + y2 + 2ax + 2by + 2b2 = 0
Question 16.
Combined equation of co-ordinate axes is:
(a) x2 – y2 = 0
(b) x2 + y2 = 0
(c) xy = c
(d) xy = 0
Answer:
(d) xy = 0
Hint:
Equation of x-axis is y = 0
Equation of y-axis is x = 0
Combine equation is xy = 0
![]()
Question 17.
ax2 + 4xy + 2y2 = 0 represents a pair of parallel lines then ‘a’ is:
(a) 2
(b) -2
(c) 4
(d) -4
Answer:
(a) 2
Hint:
Here a = 0, h = 2, b = 2
Condition for pair of parallel lines is b2 – ab = 0
4 – a(2) = 0
⇒ -2a = -4
⇒ a = 2
Question 18.
In the equation of the circle x2 + y2 = 16 then v intercept is (are):
(a) 4
(b) 16
(c) ±4
(d) ±16
Answer:
(c) ±4
Hint:
To get y-intercept put x = 0 in the circle equation we get
0 + y2 = 16
∴ y = ±4
![]()
Question 19.
If the perimeter of the circle is 8π units and centre is (2, 2) then the equation of the circle is:
(a) (x – 2)2 + (y – 2)2 = 4
(b) (x – 2)2 + (y – 2)2 = 16
(c) (x – 4)2 + (y – 4)2 = 16
(d) x2 + y2 = 4
Answer:
(c) (x – 2)2 + (y – 2)2 = 16
Hint:
Perimeter, 2πr = 8π
r = 4
Centre is (2, 2)
Equation of the circle is (x – 2)2 + (y – 2)2 = 42 = 16
Question 20.
The equation of the circle with centre (3, -4) and touches the x-axis is:
(a) (x – 3)2 + (y – 4)2 = 4
(b) (x – 3)2 + (y + 4)2 = 16
(c) (x – 3)2 + (y – 4)2 = 16
(d) x2 + y2 = 16
Answer:
(b) (x – 3)2 + (y + 4)2 = 16
Hint:
Centre (3, -4).
It touches the x-axis.
The absolute value of y-coordinate is the radius, i.e., radius = 4.
Equation is (x – 3)2 + (y + 4)2 = 16
![]()
Question 21.
If the circle touches the x-axis, y-axis, and the line x = 6 then the length of the diameter of the circle is:
(a) 6
(b) 3
(c) 12
(d) 4
Answer:
(a) 6
Hint:
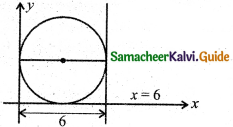
Question 22.
The eccentricity of the parabola is:
(a) 3
(b) 2
(c) 0
(d) 1
Answer:
(d) 1
![]()
Question 23.
The double ordinate passing through the focus is:
(a) focal chord
(b) latus rectum
(c) directrix
(d) axis
Answer:
(b) latus rectum
Hint:
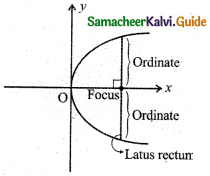
Question 24.
The distance between directrix and focus of a parabola y2 = 4ax is:
(a) a
(b) 2a
(c) 4a
(d) 3a
Answer:
(b) 2a
![]()
Question 25.
The equation of directrix of the parabola y2 = -x is:
(a) 4x + 1 = 0
(b) 4x – 1 = 0
(c) x – 1 = 0
(d) x + 4 = 0
Answer:
(b) 4x – 1 = 0
Hint:
y2 = -x.
It is a parabola open leftwards.
Here 4a = 1 ⇒ a = \(\frac{1}{4}\)
Equation of directrix is x = a.
i.e., x = \(\frac{1}{4}\) (or) 4x – 1 = 0