Samacheer Kalvi 11th Business Maths Guide Chapter 4 Trigonometry Ex 4.1

Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.1

Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.1 Text Book Back Questions and Answers

Question 1.
Convert the following degree measure into radian measure
(i) 60°
(ii) 150°
(iii) 240°
(iv) -320°
Solutions:
(i) 1°= \(\frac{\pi}{180}\) radians
∴ 60° = \(\frac{\pi}{180}\) × 60 radians = \(\frac{\pi}{3}\) radians.

(ii) 150° = \(\frac{\pi}{180}\) × 150 radians = \(\frac{5 \pi}{6}\) radians.

(iii) 240° = \(\frac{\pi}{180}\) × 240 radians = \(\frac{4 \pi}{3}\) radians.

(iv) -320° = \(\frac{\pi}{180}\) × -320 = \(\frac{-16 \pi}{9}\) radians

Question 2.
Find the degree measure corresponding to the following radian measure.
(i) \(\frac{\pi}{8}\)
(ii) \(\frac{9 \pi}{5}\)
(iii) -3
(iv) \(\frac{11 \pi}{18}\)
Solution:
We know that, one radian = \(\frac{180^{\circ}}{\pi}\)
(i) \(\frac{\pi}{8}\)
\(\frac{\pi}{8}=\frac{180^{\circ}}{\pi} \times \frac{\pi}{8}\) degrees
= \(\frac{45}{2}\)
= 22.5°
= 22°30′ [∵ 0.5° = (0.5 × 60)’ = 30′]

(ii) \(\frac{9 \pi}{5}\)
\(\frac{9 \pi}{5}=\frac{180^{\circ}}{\pi} \times \frac{9 \pi}{5}\) degrees
= 36 × 9 degrees
= 324°

(iii) -3

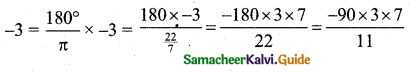
= -171.81°
= -171°48′ (∵ 0.8° = (0.8 × 60)’ = 48′)

(iv) \(\frac{11 \pi}{18}\)
\(\frac{11 \pi}{18}=\frac{180}{\pi} \times \frac{11 \pi}{18}\)
= 10 × 11°
= 110°

Question 3.
Determine the quadrants in which the following degree lie.
(i) 380°
(ii) -140°
(iii) 1195°
Solution:
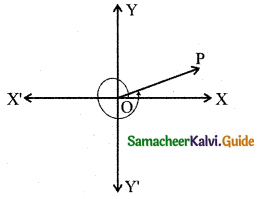
(i) 380° = 360°+ 20°
This is of the form 360° + θ
∴ After one completion of the round, the angle is 20°, 380° lies in the I quadrant.

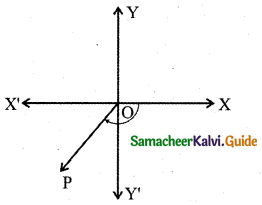
(ii) -140° = -90° + (-50°)
The angle is negative it moves in the anti-clockwise direction.
-140° lies in the III quadrants.

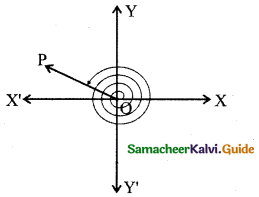
(iii) 1195° = (3 × 360°) + 90° + 25°
∴ After three completion round, the angle will lie in the II quadrant.
1195° lies in the II quadrant.

Question 4.
Find the values of each of the following trigonometric ratios.
(i) sin 300°
(ii) cos(-210°)
(iii) sec 390°
(iv) tan(-855°)
(v) cosec 1125°
Solution:
(i) sin 300° = sin(360° – 60°)
[For 360° – 60°. No change in T-ratio. 300° lies in 4th quadrant ‘sin’ is negative]
= -sin 60°
= \(-\frac{\sqrt{3}}{2}\)

(ii) cos(-210°) = cos 210° (∵ cos(-θ) = cos θ)
[∵ 180 + 30°. No change in T-ratio. 210° lies 3rd quadrant ‘cos’ is negative]
= cos(180° + 30°)
= -cos 30°
= \(-\frac{\sqrt{3}}{2}\)

(iii) sec 390° = sec(360° + 30°)
= sec 30°
= \(\frac{1}{\cos 30^{\circ}}\)
= \(\frac{1}{\left(\frac{\sqrt{3}}{2}\right)}\)
= \(\frac{2}{\sqrt{3}}\)

(iv) tan(-855°) = -tan 855° (∵ tan(-θ) = – tan θ)
[∵ Multiplies of 360° are dropped out. For 180° – 45°. No change in T-ratio. 180° – 45° lies in 2nd quadrant ‘tan’ is negative]
= -tan(2 × 360° + 135°)
= -tan 135°
= -tan(180° – 45°)
= -(-tan 45°)
= -(-1)
= 1

(v) cosec 1125° = cosec(3 × 360°+ 45°)
= cosec 45°
= \(\frac{1}{\sin 45^{\circ}}\)
= \(\frac{1}{\left(\frac{1}{\sqrt{2}}\right)}\)
= √2

Question 5.
Prove that:
(i) tan(-225°) cot(-405°) – tan(-765°) cot(675°) = 0.
(ii) 2 sin² \(\frac{\pi}{6}\) + cosec² \(\frac{7 \pi}{6}\) cos² \(\frac{\pi}{3}\) = \(\frac{3}{2}\)
(iii) \(\sec \left(\frac{3 \pi}{2}-\theta\right) \sec \left(\theta-\frac{5 \pi}{2}\right)+\tan \left(\frac{5 \pi}{2}+\theta\right) \tan \left(\theta-\frac{5 \pi}{2}\right)=-1\)
Solution:
(i) tan(-225°) = -(tan 225°)
= -(tan(180° + 45°))
= – tan 45°
= – 1
cot(-405°) = -(cot 405°)
= – cot(360° + 45°) [∵ For 360° + 45° no change in T-ratio.]
= -cot 45°
= -1
tan(-765°) = -tan 765°
= -tan(2 × 360° + 45°)
= -tan 45°
= -1
cot 675° = cot (360°+ 315°)
= cot 315°
= cot(360° – 45°)
= -cot 45°
= -1
LHS = tan(-225°) cot(-405°) – tan(-765°) cot(675°)
= (-1) (-1) – (-1) (-1)
= 1 – 1
= 0
= RHS.
Hence proved.

(ii) 2 sin² \(\frac{\pi}{6}\) + cosec² \(\frac{7 \pi}{6}\) cos² \(\frac{\pi}{3}\) = \(\frac{3}{2}\)
LHS = 2 sin² \(\frac{\pi}{6}\) + cosec² \(\frac{7 \pi}{6}\) cos² \(\frac{\pi}{3}\)
[∵ \(\frac{7 \pi}{6}\) = 210°, 210° = 180° + 30°. For 180° + 30° no change in T-ratio.
210° lies in 3rd quadrant, cosec θ is negative.]
= 2\(\left(\sin \frac{\pi}{6}\right)^{2}\) + (cosec (180° + 30°))² \(\left(\cos \frac{\pi}{3}\right)^{2}\)
= 2 \(\left(\frac{1}{2}\right)^{2}\) + (-cosec 30°)² . \(\left(\frac{1}{2}\right)^{2}\)
= \(2 \times \frac{1}{4}+(-2)^{2} \frac{1}{4}\)
= \(\frac{2}{4}+\frac{4}{4}=\frac{6}{4}\)
= \(\frac{6}{4}\)
= \(\frac{3}{2}\)
= RHS

(iii) sec(\(\frac{3 \pi}{2}\) – θ) = sec (270° – θ) = -cosec θ
[∵ For 270° – θ change T-ratio. So add ‘co’ infront ‘sec’, it becomes ‘cosec’]
sec(θ – \(\frac{5 \pi}{2}\)) = \(\sec \left(-\left(\frac{5 \pi}{2}-\theta\right)\right)\)
= sec(\(\frac{5 \pi}{2}\) – θ) [∵ sec(-θ) = θ]
= sec(450° – θ)
= sec (360° + (90° – θ))
= sec (90° – θ)
= cosec θ
[∵ For 90° – θ change in T-ratio. So add ‘co’ in front of ‘sec’ it becomes ‘cosec’]
tan(\(\frac{5 \pi}{2}\) + θ) = tan(450° + θ)
[∵ For 90° + θ, change in T-ratio. So add ‘co’ in front of ‘tan’ it becomes ‘cot’]
= tan (360° + (90° + θ))
= tan (90° + θ)
= -cot θ
\(\tan \left(\theta-\frac{5 \pi}{2}\right)=\tan \left(-\left(\frac{5 \pi}{2}-\theta\right)\right)\)
= \(-\tan \left(\frac{5 \pi}{2}-\theta\right)\) [∵ tan(-θ) = -tan θ]
= -tan(450° – θ)
= -tan(360° + (90° – θ))
= -tan(90° – θ)
= -cot θ
LHS = \(\sec \left(\frac{3 \pi}{2}-\theta\right) \sec \left(\theta-\frac{5 \pi}{2}\right)+\tan \left(\frac{5 \pi}{2}+\theta\right) \tan \left(\theta-\frac{5 \pi}{2}\right)\)
= -cosec θ (cosec θ) + (-cot θ) (-cot θ)
= -cosec² θ + cot² θ
= -(1 + cot² θ) + cot² θ [∵ 1 + cot² θ = cosec² θ]
= -1
= RHS

Question 6.
If A, B, C, D are angles of a cyclic quadrilateral, prove that: cos A + cos B + cos C + cos D = 0.
Solution:
Note: If the vertices of a quadrilateral lie on the circle then the quadrilateral is called a cyclic quadrilateral.
In a cyclic quadrilateral sum of opposite angles are 180°.

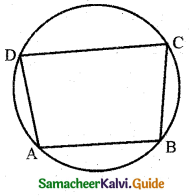
Since A, B, C, D are angles of cyclic quadrilateral
A + C = 180° and B + D = 180°
LHS = cos A + cos B + cos C + cos D
= cos A + cos B + cos(180° – A) + cos(180° – B)
= cos A + cos B – cos A – cos B
= 0
= RHS

Question 7.
Prove that

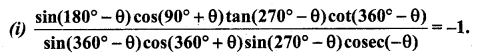
(ii) sin θ . cos{sin(\(\frac{\pi}{2}\) – θ) . cosec θ + cos(\(\frac{\pi}{2}\) – θ) . sec θ} = 1
Solution:

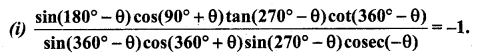
(ii) sin θ . cos{sin(\(\frac{\pi}{2}\) – θ) . cosec θ + cos(\(\frac{\pi}{2}\) – θ) . sec θ} = 1

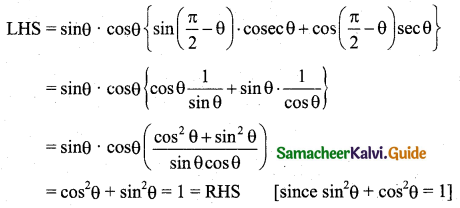
Question 8.
Prove that: cos 510° cos 330° + sin 390° cos 120° = -1.
Solution:
LHS = cos 510° cos 330° + sin 390° cos 120°
= cos(360° + 150°) cos(360° – 30°) + sin(360° + 30°) × cos(180° – 60°)
= cos 150° cos 30° + sin 30° (-cos 60°)
= cos(180° – 30°) cos 30° + sin 30° cos 60°
= -cos 30° cos 30° + \(\frac{1}{2} \times\left(\frac{-1}{2}\right)\)
= \(-\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}-\frac{1}{2} \times \frac{1}{2}\)
= \(-\frac{3}{4}-\frac{1}{4}\)
= \(\frac{-3-1}{4}\)
= -1

Question 9.
Prove that:
(i) tan(π + x) cot(x – π) – cos(2π – x) cos(2π + x) = sin² x.

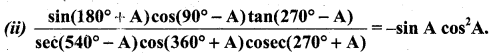
Solution:
(i) tan(π + x) cot(x – π) – cos(2π – x) cos(2π + x) = (tan x) (-cot(π – x) – cos x cos x
[∵ cot(x – π) = cot(-(π – x)) = -cot(π – x) = cot x]
= tan x cot x – cos² x
= 1 – cos² x
= sin² x [∵ sin² x + cos² x = 1 ⇒ sin² x = (1 – cos² x)]

Question 10.
If sin θ = \(\frac{3}{5}\), tan φ = \(\frac{1}{2}\) and \(\frac{\pi}{2}\) < θ < π < φ < \(\frac{3 \pi}{2}\), then find the value of 8 tan θ – √5 sec φ.
Solution:

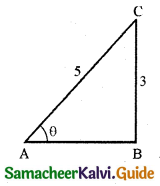
Given that sin θ = \(\frac{3}{5}=\frac{\text { Opposite side }}{\text { Hypotenuse }}\)
∵ AB = \(\sqrt{5^{2}-3^{2}}=\sqrt{25-9}=\sqrt{16}\) = 4
Here θ lies in second quadrant [∵ \(\frac{\pi}{2}\) < θ < π]
∵ tan θ is negative.
tan θ = \(-\frac{3}{4}\)
Also given that tan Φ = \(\frac{1}{2}=\frac{\text { Opposite side }}{\text { Adjacent side }}\)
∴ PR = \(\sqrt{\mathrm{PQ}^{2}+\mathrm{QP}^{2}}=\sqrt{4+1}=\sqrt{5}\)
Here Φ lies in third quadrant (∵ π < Φ < \(\frac{3 \pi}{2}\))
∴ sec Φ is negative.
\(\sec \phi=\frac{1}{\cos \phi}=-\frac{1}{\left(\frac{2}{\sqrt{5}}\right)}=-\frac{\sqrt{5}}{2}\)
Now 8 tan θ – √5 sec Φ = \(8\left(-\frac{3}{4}\right)-\sqrt{5}\left(\frac{-\sqrt{5}}{2}\right)\)
= 2 × (-3) + \(\frac{5}{2}\)
= -6 + \(\frac{5}{2}\)
= \(\frac{-12+5}{2}\)
= \(\frac{-7}{2}\)