Samacheer Kalvi 11th Business Maths Guide Chapter 4 Trigonometry Ex 4.5

Students can download 11th Business Maths Chapter 4 Trigonometry Ex 4.5 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 4 Trigonometry Ex 4.5

Samacheer Kalvi 11th Business Maths Trigonometry Ex 4.5 Text Book Back Questions and Answers

Question 1.
The degree measure of \(\frac{\pi}{8}\) is:
(a) 20°60′
(b) 22°30′
(c) 22°60′
(d) 20°30′
Answer:
(b) 22°30′
Hint:
We know that, one radian = \(\frac{180^{\circ}}{\pi}\)
∴ \(\frac{\pi}{8}=\frac{180^{\circ}}{\pi} \times \frac{\pi}{8}\) degrees
= \(\frac{45^{\circ}}{2}\)
= 22.5°
= 22°30′

Question 2.
The radian measure of 37°30′ is:
(a) \(\frac{5 \pi}{24}\)
(b) \(\frac{3 \pi}{24}\)
(c) \(\frac{7 \pi}{24}\)
(d) \(\frac{9 \pi}{24}\)
Answer:
(a) \(\frac{5 \pi}{24}\)
Hint:

Question 3.
If tan θ = \(\frac{1}{\sqrt{5}}\) and θ lies in the first quadrant then cos θ is:
(a) \(\frac{1}{\sqrt{6}}\)
(b) \(\frac{-1}{\sqrt{6}}\)
(c) \(\frac{\sqrt{5}}{\sqrt{6}}\)
(d) \(\frac{-\sqrt{5}}{\sqrt{6}}\)
Answer:
(c) \(\frac{\sqrt{5}}{\sqrt{6}}\)
Hint:

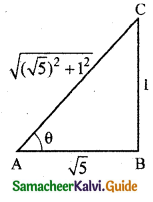
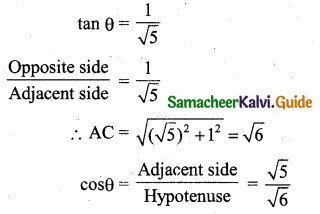
Question 4.
The value of sin 15° is:
(a) \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\)
(b) \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
(c) \(\frac{\sqrt{3}}{\sqrt{2}}\)
(d) \(\frac{\sqrt{3}}{2 \sqrt{2}}\)
Answer:
(b) \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
Hint:
sin 15° = sin(45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
= \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}} \times \frac{1}{2}\)
= \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

Question 5.
The value of sin(-420°)
(a) \(\frac{\sqrt{3}}{2}\)
(b) \(-\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{-1}{2}\)
Answer:
(b) \(-\frac{\sqrt{3}}{2}\)
Hint:
sin(-420°) = -sin(420°) [∵ sin(-θ) = -sin θ]
= -sin(360° + 60°)
= -sin 60°
= \(-\frac{\sqrt{3}}{2}\)

Question 6.
The value of cos(-480°) is:
(a) √3
(b) \(-\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{-1}{2}\)
Answer:
(d) \(\frac{-1}{2}\)
Hint:
cos(-480°) = cos 480° [∵ cos(-θ) = cos θ]
= cos(360° + 120°)
= cos 120°
= cos(180° – 60°)
= -cos 60°
= \(\frac{-1}{2}\)

Question 7.
The value of sin 28° cos 17° + cos 28° sin 17°
(a) \(\frac{1}{\sqrt{2}}\)
(b) 1
(c) \(\frac{-1}{\sqrt{2}}\)
(d) 0
Answer:
(a) \(\frac{1}{\sqrt{2}}\)
Hint:
sin 28° cos 17° + cos 28° sin 17° = sin(28° + 17°)
This is of the form sin(A + B), A = 28°, B = 17°
= sin 45°
= \(\frac{1}{\sqrt{2}}\)

Question 8.
The value of sin 15° cos 15° is:
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{\sqrt{3}}{2}\)
(d) \(\frac{1}{4}\)
Answer:
(d) \(\frac{1}{4}\)
Hint:
sin 15° cos 15° = \(\frac{1}{2}\) (2 sin 15° cos 15°)
= \(\frac{1}{2}\) (sin 30°)
= \(\frac{1}{2}\left(\frac{1}{2}\right)\)
= \(\frac{1}{4}\)

Question 9.
The value of sec A sin(270° + A) is:
(a) -1
(b) cos² A
(c) sec² A
(d) 1
Answer:
(a) -1
Hint:
sec A (sin(270° + A)) = \(\frac{1}{\cos A}\) (-cos A) = -1

Question 10.
If sin A + cos A = 1 then sin 2A is equal to:
(a) 1
(b) 2
(c) 0
(d) \(\frac{1}{2}\)
Answer:
(c) 0
Hint:
Given sin A + cos A = 1
Squaring both sides we get
sin² A + cos² A + 2 sin A cos A = 1
1 + sin 2A = 1
sin 2A = 0

Question 11.
The value of cos² 45° – sin² 45° is:
(a) \(\frac{\sqrt{3}}{2}\)
(b) \(\frac{1}{2}\)
(c) 0
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(c) 0
Hint:
cos² 45° – sin² 45°
= cos 2 × 45° (∵ cos² A – sin² A = cos 2A)
= cos 90°
= 0

Question 12.
The value of 1 – 2 sin² 45° is:
(a) 1
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) 0
Answer:
(d) 0
Hint:
1 – 2 sin² 45°
= cos(2 × 45°) [∵ cos 2A = 1 – 2 sin² A]
= cos 90°
= 0

Question 13.
The value of 4 cos³ 40° – 3 cos 40° is
(a) \(\frac{\sqrt{3}}{2}\)
(b) \(-\frac{1}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(b) \(-\frac{1}{2}\)
Hint:
4 cos³ 40° – 3 cos 40°
= cos (3 × 40°) [∵ cos 3A = 4 cos³ A – 3 cos A]
= cos 120°
= cos (180° – 60°)
= -cos 60°
= \(-\frac{1}{2}\)

Question 14.
The value of \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\) is:
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{\sqrt{3}}\)
(c) \(\frac{\sqrt{3}}{2}\)
(d) √3
Answer:
(d) √3
Hint:
We know that sin 2A = \(\frac{2 \tan A}{1+\tan ^{2} A}\)
\(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\) = sin(2 × 30°) = sin 60° = \(\frac{\sqrt{3}}{2}\)
= tan 2A
= tan 60°
= √3

Question 15.
If sin A = \(\frac{1}{2}\) then 4 cos³ A – 3 cos A is:
(a) 1
(b) 0
(c) \(\frac{\sqrt{3}}{2}\)
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(b) 0
Hint:
Given sin A = \(\frac{1}{2}\)
sin A = sin 30°
∴ A = 30°
[∵ 4 cos³ A – 3 cos A = cos 3A]
= cos(3 × 30°)
= cos 90°
= 0

Question 16.
The value of \(\frac{3 \tan 10^{\circ}-\tan ^{3} 10^{\circ}}{1-3 \tan ^{2} 10^{\circ}}\) is:
(a) \(\frac{1}{\sqrt{3}}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{\sqrt{3}}{2}\)
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(a) \(\frac{1}{\sqrt{3}}\)
Hint:
\(\frac{3 \tan 10^{\circ}-\tan ^{3} 10^{\circ}}{1-3 \tan ^{2} 10^{\circ}}\) = tan(3 × 10°) [∵ tan 3A = \(\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}\)]
= tan 30°
= \(\frac{1}{\sqrt{3}}\)

Question 17.
The value of cosec^-1 (\(\frac{2}{\sqrt{3}}\)) is:
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{3}\)
(d) \(\frac{\pi}{6}\)
Answer:
(c) \(\frac{\pi}{3}\)
Hint:
Let cosec^-1 (\(\frac{2}{\sqrt{3}}\))
\(\frac{2}{\sqrt{3}}\) = cosec A
cosec A = \(\frac{2}{\sqrt{3}}\)
sin A = \(\frac{\sqrt{3}}{2}\) = sin 60°
∴ A = 60° = \(\frac{\pi}{3}\)

Question 18.
sec^-1 (\(\frac{2}{3}\)) + cosec^-1 (\(\frac{2}{3}\)) =
(a) \(\frac{-\pi}{2}\)
(b) \(\frac{\pi}{2}\)
(c) π
(d) -π
Answer:
(b) \(\frac{\pi}{2}\)
Hint:
We know that sec^-1 x + cosec^-1 x = \(\frac{\pi}{2}\)
∴ sec^-1 (\(\frac{2}{3}\)) + cosec^-1 (\(\frac{2}{3}\)) = \(\frac{\pi}{2}\)

Question 19.
If α and β be between 0 and \(\frac{\pi}{2}\) and if cos(α + β) = \(\frac{12}{13}\) and sin(α – β) = \(\frac{3}{5}\) then sin 2α is:
(a) \(\frac{16}{15}\)
(b) 0
(c) \(\frac{56}{65}\)
(d) \(\frac{64}{65}\)
Answer:
(c) \(\frac{56}{65}\)
Hint:

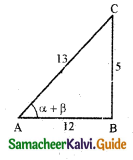
Given that cos(α + β) = \(\frac{12}{13}\)
∴ sin(α + β) = \(\frac{5}{13}\)

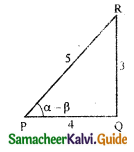
Also given that sin(α – β) = \(\frac{3}{5}\)
∴ cos(α – β) = \(\frac{4}{5}\)
sin 2α = sin[(α + β) + (α – β)]
= sin(α + β) cos(α – β) + cos(α + β) sin(α – β)
= \(\frac{5}{13} \times \frac{4}{5}+\frac{12}{13} \times \frac{3}{5}\)
= \(\frac{20}{65}+\frac{36}{65}\)
= \(\frac{56}{65}\)

Question 20.
If tan A = \(\frac{1}{2}\) and tan B = \(\frac{1}{3}\) then tan(2A + B) is equal to:
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3
Hint:
Given tan A = \(\frac{1}{2}\), tan B = \(\frac{1}{3}\)

Question 21.
tan(\(\frac{\pi}{4}\) – x) is:
(a) \(\left(\frac{1+\tan x}{1-\tan x}\right)\)
(b) \(\left(\frac{1-\tan x}{1+\tan x}\right)\)
(c) 1 – tan x
(d) 1 + tan x
Answer:
(b) \(\left(\frac{1-\tan x}{1+\tan x}\right)\)
Hint:

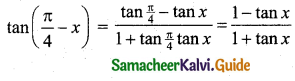
[∵ tan \(\frac{\pi}{4}\) = 1]

Question 22.
\(\sin \left(\cos ^{-1} \frac{3}{5}\right)\) is:
(a) \(\frac{3}{5}\)
(b) \(\frac{5}{3}\)
(c) \(\frac{4}{5}\)
(d) \(\frac{5}{4}\)
Answer:
(c) \(\frac{4}{5}\)
Hint:

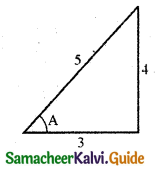
Let cos^-1 (\(\frac{3}{5}\)) = A
\(\frac{3}{5}\) = cos A
sin A = \(\frac{4}{5}\)
Now sin(cos-1 (\(\frac{3}{5}\))) = sin A = \(\frac{4}{5}\)

Question 23.
The value of \(\frac{1}{cosec(-45^{\circ})}\) is:
(a) \(\frac{-1}{\sqrt{2}}\)
(b) \(\frac{1}{\sqrt{2}}\)
(c) √2
(d) -√2
Answer:
(a) \(\frac{-1}{\sqrt{2}}\)
Hint:
\(\frac{1}{cosec(-45^{\circ})}\) = sin(-45°)
= -sin 45°
= \(\frac{-1}{\sqrt{2}}\)

Question 24.
If p sec 50° = tan 50° then p is:
(a) cos 50°
(b) sin 50°
(c) tan 50°
(d) sec 50°
Answer:
(b) sin 50°
Hint:
p sec 50° = tan 50°
p(\(\frac{1}{\cos 50^{\circ}}\)) = \(\frac{\sin 50^{\circ}}{\cos 50^{\circ}}\)
∴ p = sin 50°

Question 25.
(\(\frac{cos x}{cosec x})-\sqrt{1-\sin ^{2} x} \sqrt{1-\cos ^{2} x}\) is:
(a) cos² x – sin² x
(b) sin² x – cos² x
(c) 1
(d) 0
Answer:
(d) 0
Hint:
(\(\frac{cos x}{cosec x})-\sqrt{1-\sin ^{2} x} \sqrt{1-\cos ^{2} x}\)
= cos x × sin x – \(\sqrt{\cos ^{2} x} \sqrt{\sin ^{2} x}\)
= cos x × sin x – cos x × sin x
= 0