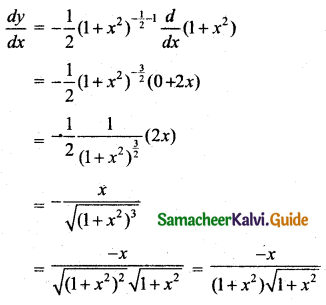Samacheer Kalvi 11th Business Maths Guide Chapter 5 Differential Calculus Ex 5.5

Students can download 11th Business Maths Chapter 5 Differential Calculus Ex 5.5 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 5 Differential Calculus Ex 5.5

Samacheer Kalvi 11th Business Maths Differential Calculus Ex 5.5 Text Book Back Questions and Answers

Question 1.
Differentiate the following with respect to x.
(i) 3x⁴ – 2x³ + x + 8
(ii) \(\frac{5}{x^{4}}-\frac{2}{x^{3}}+\frac{5}{x}\)
(iii) \(\sqrt{x}+\frac{1}{\sqrt[3]{x}}+e^{x}\)
(iv) \(\frac{3+2 x-x^{2}}{x}\)
(v) x³ e^x
(vi) (x² – 3x + 2) (x + 1)
(vii) x⁴ – 3 sin x + cos x
(viii) \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}\)
Solution:
(i) Let y = 3x⁴ – 2x³ + x + 8

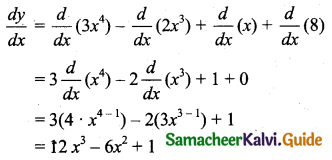
(ii) Let y = \(\frac{5}{x^{4}}-\frac{2}{x^{3}}+\frac{5}{x}\)

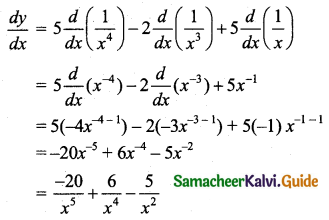
(iii) Let y = \(\sqrt{x}+\frac{1}{\sqrt[3]{x}}+e^{x}\)
\(y=x^{\frac{1}{2}}+x^{\frac{1}{3}}+e^{x}\)
[∵ \(\frac{1}{\sqrt[3]{x}}=\frac{1}{(x)^{\frac{1}{3}}}=x^{\frac{1}{3}}\)]

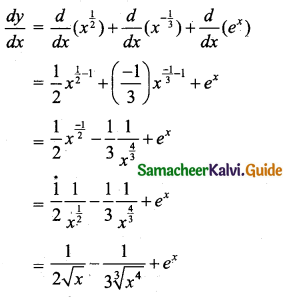
(iv) Let y = \(\frac{3+2 x-x^{2}}{x}\)

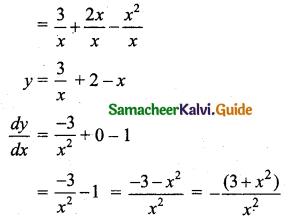
(v) Let y = x³ e^x
[∵ We have product of two functions, so use product rule]
= x³ e^x + e^x (3x²)
= e^x (x³ + 3x²)
= x² e^x (x + 3)

(vi) Let y = (x² – 3x + 2) (x + 1)
y = x³ – 3x² + 2x + x² – 3x + 2
y = x³ – 2x² – x + 2
\(\frac{dy}{dx}\) = 3x² – 4x – 1

(vii) Let y = x⁴ – 3 sin x + cos x
\(\frac{dy}{dx}\) = \(\frac{d}{d x}\) (x4) – 3 \(\frac{d}{d x}\) (sin x) + \(\frac{d}{d x}\) (cos x)
= 4x³ – 3 cos x – sin x

(viii) \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}\)

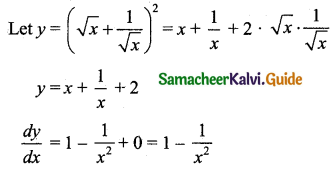
Question 2.
Differentiate the following with respect to x.
(i) \(\frac{e^{x}}{1+x}\)
(ii) \(\frac{x^{2}+x+1}{x^{2}-x+1}\)
(iii) \(\frac{e^{x}}{1+e^{x}}\)
Solution:
(i) Let y = \(\frac{e^{x}}{1+x}\)

(ii) Let y = \(\frac{x^{2}+x+1}{x^{2}-x+1}\)

(iii) Let y = \(\frac{e^{x}}{1+e^{x}}\)

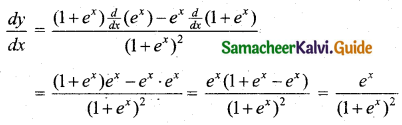
Question 3.
Differentiate the following with respect to x.
(i) x sin x
(ii) e^x sin x
(iii) e^x (x + log x)
(iv) sin x cos x
(v) x³ e^x
Solution:
(i) Let y = x sin x
\(\frac{d y}{d x}\) = x \(\frac{d}{d x}\) (sin x) + sin x \(\frac{d}{d x}\) (x)
= x cos x + sin x . 1
= x cos x + sin x

(ii) Let y = e^x sin x
\(\frac{d y}{d x}\) = e^x \(\frac{d}{d x}\) (sin x) + sin x \(\frac{d}{d x}\) (e^x)
= e^x cos x + sin x e^x
= e^x (cos x + sin x)

(iii) Let y = e^x (x + log x)

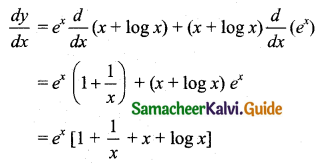
(iv) Let y = sin x cos x
\(\frac{d y}{d x}\) = sin x \(\frac{d}{d x}\) (cos x) + cos x \(\frac{d}{d x}\) (sin x)
= sin x (-sin x) + cos x cos x
= -sin² x + cos² x
= cos² x – sin² x
= cos 2x [∵ cos 2x = cos² x – sin² x]
(or) y = sin x cos x
y = \(\frac{1}{2}\) (2 sin x cos x)
y = \(\frac{1}{2}\) sin 2x
\(\frac{d y}{d x}\) = \(\frac{1}{2}\) cos 2x . 2 = cos 2x

(v) Let y = x³ e^x
\(\frac{d y}{d x}\) = x³ \(\frac{d}{d x}\) (e^x) + e^x \(\frac{d}{d x}\) (x³)
= x³ (e^x) + e^x (3x²)
= x² e^x (x + 3)

Question 4.
Differentiate the following with respect to x.
(i) sin² x
(ii) cos² x
(iii) cos³ x
(iv) \(\sqrt{1+x^{2}}\)
(v) (ax² + bx + c)ⁿ
(vi) sin(x²)
(vii) \(\frac{1}{\sqrt{1+x^{2}}}\)
Solution:
For the following problems chain rule to be used:
\(\frac{d}{d x}\) f(g(x)) = f'(g(x)) . g'(x)
\(\frac{d}{d x}\) [f(x)]ⁿ = n[f(x)]^n-1 × \(\frac{d}{d x}\) f(x)
(i) Let y = sin² x = (sin x)²
\(\frac{d y}{d x}\) = 2(sin x)^2-1 \(\frac{d}{d x}\) (sin x)
= 2 sin x (cos x)
= sin 2x

(ii) y = cos² x = (cos x)²
\(\frac{d y}{d x}\) = 2(cos x)^2-1 \(\frac{d}{d x}\) (cos x)
= 2 cos x (-sin x)
= -2 sin x cos x
= -sin 2x

(iii) y = cos³ x
y = (cos x)³
\(\frac{d y}{d x}\) = 3(cos x)^3-1 \(\frac{d}{d x}\) (cos x)
= 3 cos² x (-sin x)
= -3 cos² x sin x
= -3 cos x (sin x cos x) [Multiply and divide by 2]
= \(\frac{-3}{2}\) cos x (2 sin x cos x)
= \(\frac{-3}{2}\) cos x sin 2x

(iv) Let y = \(\sqrt{1+x^{2}}\)
y = \(\left(1+x^{2}\right)^{\frac{1}{2}}\)
Here f(x) = 1 + x²; n = \(\frac{1}{2}\)

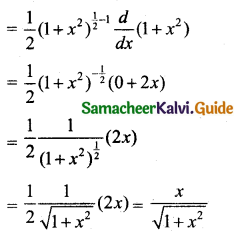
(v) Let y = (ax² + bx + c)ⁿ
\(\frac{d y}{d x}\) = n(ax² + bx + c)^n-1 \(\frac{d}{d x}\) (ax² + bx + c)
= n(ax² + bx + c)^n-1 (2ax + b)

(vi) Let y = sin(x²)
\(\frac{d}{d x}\) f(g(x)) = f'(g(x)) . g'(x)
Here f = sin x, g = x²
\(\frac{d y}{d x}\) = cos(x²) \(\frac{d}{d x}\) (x²)
= cos(x²) (2x)
= 2x cos(x²)

(vii) Let y = \(\frac{1}{\sqrt{1+x^{2}}}\)
y = \(\left(1+x^{2}\right)^{-\frac{1}{2}}\)
Here n = \(-\frac{1}{2}\); f(x) = 1 + x²