Students can download 11th Business Maths Chapter 6 Applications of Differentiation Ex 6.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 6 Applications of Differentiation Ex 6.1
Samacheer Kalvi 11th Business Maths Applications of Differentiation Ex 6.1 Text Book Back Questions and Answers
Question 1.
A firm produces x tonnes of output at a total cost of C(x) = \(\frac{1}{10}\) x3 – 4x2 – 20x + 7 find the
(i) average cost
(ii) average variable cost
(iii) average fixed cost
(iv) marginal cost and
(v) marginal average cost.
Solution:
c(x) = f(x) + x
c(x) = \(\frac{1}{10}\) x3 – 4x2 – 20x + 7
Then f(x) = \(\frac{1}{10}\) x3 – 4x2 – 20x and k = 7
(i) Average Cost (AC) = \(\frac{\text { Total cost }}{\text { Output }}=\frac{C(x)}{x}=\frac{f(x)+k}{x}\)
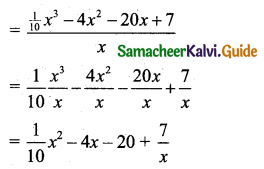
(ii) Average Variable Cost (AVC) = \(\frac{\text { Variable cost }}{\text { Output }}=\frac{f(x)}{x}\)
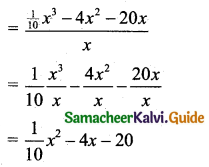
(iii) Average Fixed Cost (AFC) = \(\frac{\text { Fixed cost }}{\text { Output }}=\frac{k}{x}=\frac{7}{x}\)
(iv) Marginal Cost (MC) = \(\frac{d \mathrm{C}}{d x}\)
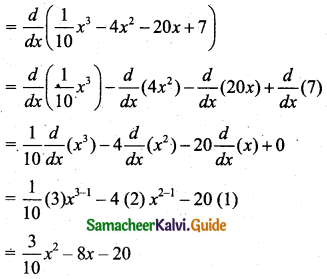
(v) Marginal Average Cost (MAC) = \(\frac{d}{d x}\) (AC)
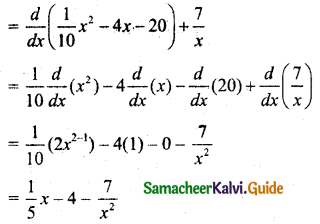
![]()
Question 2.
The total cost of x units of output of a firm is given by C = \(\frac{2}{3} x+\frac{35}{2}\). Find the
(i) cost when output is 4 units
(ii) average cost when output is 10 units
(ii) marginal cost when output is 3 units
Solution:
C = \(\frac{2}{3} x+\frac{35}{2}\)
i.e., C(x) = \(\frac{2}{3} x+\frac{35}{2}\)
(i) Cost when output is 4 units, i.e., to find when x = 4, C = ?
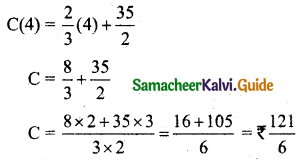
(ii) Average cost when output is 10 units, i.e., to find when x = 10, AC = ?

Average cost when output is 10 units is ₹ \(\frac{29}{12}\)
(iii) Marginal cost when output is 3 units
C = \(\frac{2}{3} x+\frac{35}{2}\)
Marginal Cost (MC) = \(\frac{d}{d x}\) (C)
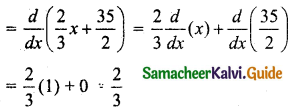
Marginal cost when output is 3 units will be ₹ \(\frac{2}{3}\)
Question 3.
Revenue function ‘R’ and cost function ‘C’ are R = 14x – x2 and C = x(x2 – 2). Find the
(i) average cost
(ii) marginal cost
(iii) average revenue and
(iv) marginal revenue.
Solution:
R = 14x – x2 and C = x(x2 – 2)
C = x3 – 2x
(i) Average Cost (AC) = \(\frac{\text { Total cost }}{\text { Output }}=\frac{C(x)}{x}\)
= \(\frac{x^{3}-2 x}{x}\)
= \(\frac{x^{3}}{x}-\frac{2 x}{x}\)
= x2 – 2
(ii) Marginal Cost (MC) = \(\frac{d \mathrm{C}}{d x}\)
= \(\frac{d}{d x}\) (x3 – 2x)
= \(\frac{d}{d x}\) (x3) – 2 \(\frac{d}{d x}\) (x)
= 3x2 – 2
(iii) Average Revenue R = 14x – x2
Average Revenue (AR) = \(\frac{\text { Total Revenue }}{\text { Output }}=\frac{\mathrm{R}(x)}{x}\)
= \(\frac{14 x-x^{2}}{x}\)
= \(\frac{14 x}{x}-\frac{x^{2}}{x}\)
= 14 – x
(iv) Marginal Revenue (MR) = \(\frac{d \mathrm{R}}{d x}\)
= \(\frac{d}{d x}\) (14x – x2)
= 14 \(\frac{d}{d x}\) (x) – \(\frac{d}{d x}\) (x2)
= 14(1) – 2x
= 14 – 2x
![]()
Question 4.
If the demand law is given by p = 10\(e^{-\frac{x}{2}}\) then find the elasticity of demand.
Solution:
p = 10\(e^{-\frac{x}{2}}\)
Elasticity of demand: ηd = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
p = 10\(e^{-\frac{x}{2}}\)
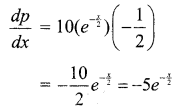
Elasticity of demand: ηd = \(-\frac{p}{x} \cdot \frac{1}{\left(\frac{d p}{d x}\right)}\)
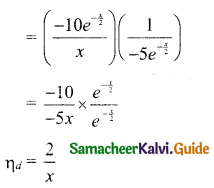
Question 5.
Find the elasticity of demand in terms of x for the following demand laws and also find the value of x where elasticity is equals to unity.
(i) p = (a – bx)2
(ii) p = a – bx2
Solution:
(i) p = (a – bx)2
= \(\frac{d p}{d x}=2(a-b x)^{2-1} \frac{d}{d x}(a-b x)\)
= 2(a – bx) (0 – b(1))
= -2b(a – bx)
Elasticity of demand: ηd = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
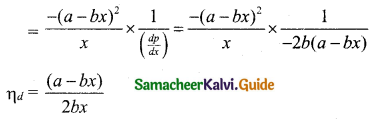
When the elasticity of demand is equals to unity,
\(\frac{a-b x}{2 b x}\) = 1
a – bx = 2bx
2bx = a – bx
2bx + bx = a
3bx = a
x = \(\frac{a}{3 b}\)
∴ The value of x when elasticity is equal to unity is \(\frac{a}{3 b}\)
(ii) p = a – bx2
\(\frac{d p}{d x}=0-b \frac{d}{d x}\left(x^{2}\right)\)
= -b(2x)
= -2bx
Elasticity of demand: ηd = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
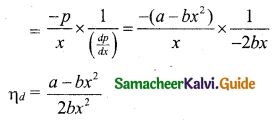
When elasticity is equals to unit,
\(\frac{a-b x^{2}}{2 b x^{2}}\) = 1
a – bx2 = 2bx2
2bx2 = a – bx2
2bx2 + bx2 = a
3bx2 = a
x2 = \(\frac{a}{3 b}\)
x = \(\sqrt{\frac{a}{3 b}}\)
∴ The value of x when elasticity is equal to unity is \(\sqrt{\frac{a}{3 b}}\)
![]()
Question 6.
Find the elasticity of supply for the supply function x = 2p2 + 5 when p = 3.
Solution:
x = 2p2 + 5
\(\frac{d x}{d p}\) = 2 × 2p + 0 = 4p
Elasticity of supply: ηs = \(\frac{p}{x} \cdot \frac{d x}{d p}\)
= \(\frac{p}{2 p^{2}+5} \times 4 p\)
= \(\frac{4 p^{2}}{2 p^{2}+5}\)
When p = 3, elasticity of supply, ηs = \(\frac{4 \times 3^{2}}{2(3)^{2}+5}\)
= \(\frac{4 \times 9}{18+5}\)
= \(\frac{36}{23}\)
Question 7.
The demand curve of a commodity is given by p = \(\frac{50-x}{5}\), find the marginal revenue for any output x and also find marginal revenue at x = 0 and x = 25?
Solution:
Given that p = \(\frac{50-x}{5}\)
Revenue, R = px
= \(\left(\frac{50-x}{5}\right) x\)
= \(\frac{50 x-x^{2}}{5}\)
= \(\frac{1}{5}\) (50x – x2)
Marginal Revenue (MR) = \(\frac{d}{d x}\) (R)
= \(\frac{d}{d x}\) \(\frac{1}{5}\) (50x – x2)
= \(\frac{1}{5}\) \(\frac{d}{d x}\) (50x – x2)
= \(\frac{1}{5}\) (50 – 2x)
Marginal revenue when x = 0 is, MR = \(\frac{1}{5}\) (50 – 2 × 0)
= \(\frac{1}{5}\) × 50
= 10
When x = 25, marginal revenue is MR = \(\frac{1}{5}\) (50 – 2 × 25)
= \(\frac{1}{5}\) (50 – 50)
= 0
![]()
Question 8.
The supply function of certain goods is given by x = a\(\sqrt{p-b}\) where p is unit price, a and b are constants with p > b. Find elasticity of supply at p = 2b.
Solution:
Given that x = a\(\sqrt{p-b}\)
Elasticity of supply: ηs = \(\frac{p}{x} \cdot \frac{d x}{d p}\)

Hint for differentiation
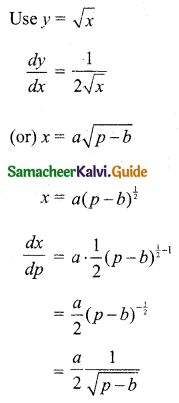
When p = 2b, Elasticity of supply: ηs = \(\frac{2 b}{2(2 b-b)}=\frac{2 b}{2 b}=1\)
Question 9.
Show that MR = p \(\left[1-\frac{\mathbf{1}}{\eta_{d}}\right]\) for the demand function p = 400 – 2x – 3x2 where p is unit price and x is quantity demand.
Solution:
Given p = 400 – 2x – 3x2
Revenue, R = px = (400 – 2x – 3x2)x = 400x – 2x2 – 3x3
Marginal Revenue (MR) = \(\frac{d}{d x}\) (R)
= \(\frac{d}{d x}\) (400x – 2x2 – 3x3)
= 400 – 4x – 9x2


Thus for the function p = 400 – 2x – 3x2
MR = \(p\left[1-\frac{1}{\eta_{d}}\right]\)
![]()
Question 10.
For the demand function p = 550 – 3x – 6x2 where x is quantity demand and p is unit price. Show that MR = \(p\left[1-\frac{1}{\eta_{d}}\right]\)
Solution:
Given p = 550 – 3x – 6x2
Revenue, R = px = (550 – 3x – 6x2)x = 550x – 3x2 – 6x3
Marginal Revenue (MR) = \(\frac{d}{d x}\) (R)
= \(\frac{d}{d x}\) (550x – 3x2 – 6x3)
= 550 – 6x- 18x2
Now ηd = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
p = 550 – 3x – 6x2
\(\frac{d p}{d x}\) = 0 – 3 – 12x
∴ ηd = \(-\frac{p}{x} \cdot \frac{1}{\left(\frac{d p}{d x}\right)}\)

Question 11.
For the demand function x = \(\frac{25}{p^{4}}\), 1 ≤ p ≤ 5, determine the elasticity of demand.
Solution:
The demand function, x = \(\frac{25}{p^{4}}\), 1 ≤ p ≤ 5
The elasticity demand, ηd = \(-\frac{p}{x} \cdot \frac{d x}{d p}\)
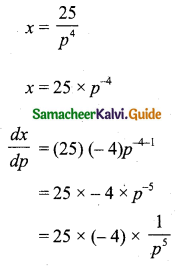
Hint for differentiation
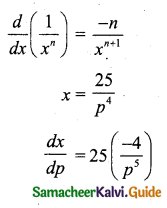
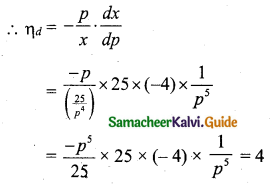
![]()
Question 12.
The demand function of a commodity is p = 200 – \(\frac{x}{100}\) and its cost is C = 40x + 120 where p is a unit price in rupees and x is the number of units produced and sold. Determine
(i) profit function
(ii) average profit at an output of 10 units
(iii) marginal profit at an output of 10 units and
(iv) marginal average profit at an output of 10 units.
Solution:
The demand function, p = 200 – \(\frac{x}{100}\)
Cost is C = 40x + 120
Revenue function, R(x) = px
= \(\left(200-\frac{x}{100}\right) x\)
= 200x – \(\frac{x^{2}}{100}\)
(i) Profit function = R(x) – C(x)
= 200x – \(\frac{x^{2}}{100}\) – (40x + 120)
= 200x – \(\frac{x^{2}}{100}\) – 40x – 120
= 160x – \(\frac{x^{2}}{100}\) – 120
(ii) Average profit (AP) = \(\frac{\text { Total Profit }}{\text { Output }}\)
= \(\frac{1}{x}\left(160 x-\frac{x^{2}}{100}-120\right)\)
= \(160-\frac{x}{100}-\frac{120}{x}\)
Average profit at an output of 10 units
When x = 10, average profit = 160 – \(\frac{10}{100}-\frac{120}{10}\)
= 160 – \(\frac{1}{10}\) – 12
= 148 – \(\frac{1}{10}\)
= 148 – 0.1
= ₹ 147.9
(iii) Marginal profit [MP] = \(\frac{d \mathrm{P}}{x}\)
= \(\frac{d}{d x}\left(160 x-\frac{x^{2}}{100}-120\right)\)
= 160 – \(\frac{2 x}{100}\)
= 160 – \(\frac{x}{50}\)
Marginal profit when x = 10, is = 160 – \(\frac{10}{50}\)
= 160 – \(\frac{1}{5}\)
= 160 – 0.2
= ₹ 159.8
(iv) Average profit AP = 160 – \(\frac{x}{100}-\frac{120}{x}\)
Marginal average profit (MAP) = \(\frac{d}{d x}\) (AP)
= \(\frac{d}{d x}\left(160-\frac{x}{100}-\frac{120}{x}\right)\)
= 0 – \(\frac{1}{100}-120\left(-\frac{1}{x^{2}}\right)\) [∵ \(\frac{d}{d x}\left(\frac{1}{x}\right)=\frac{-1}{x^{2}}\)]
= \(\frac{-1}{100}+\frac{120}{x^{2}}\)
When x = 10, marginal average profit is = \(-\frac{1}{100}+\frac{120}{10^{2}}\)
= \(\frac{-1}{100}+\frac{120}{100}\)
= \(\frac{-1+120}{100}\)
= \(\frac{119}{100}\)
= ₹ 1.19
Question 13.
Find the values of x, when the marginal function of y = x3 + 10x2 – 48x + 8 is twice the x.
Solution:
y = x3 + 10x2 – 48x + 8
Marginal function, \(\frac{d y}{d x}\) = 3x2 + 10(2x) – 48
= 3x2 + 20x – 48
Given that, the marginal function is twice the x.
Therefore, 3x2 + 20x – 48 = 2x
3x2 + 18x – 48 = 0
Divide throughout by 3, x2 + 6x – 16 = 0
(x + 8) (x – 2) = 0
x = -8 (or) x = 2
The values of x are -8, 2.
![]()
Question 14.
The total cost function y for x units is given by y = 3x\(\left(\frac{x+7}{x+5}\right)\) + 5. Show that the marginal cost decreases continuously as the output increases.
Solution:
The total cost function, y = 3x\(\left(\frac{x+7}{x+5}\right)\) + 5
To prove the marginal cost decreases continuously as the output increase we should prove \(\frac{d y}{d x}\) is positive.
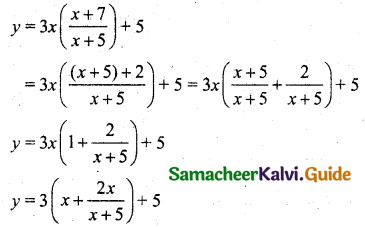
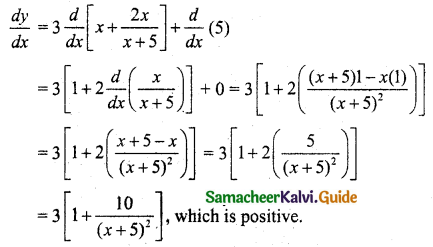
∴ The marginal cost decreases continuously of the output increases.
Question 15.
Find the price elasticity of demand for the demand function x = 10 – p where x is the demand p is the price. Examine whether the demand is elastic, inelastic, or unit elastic at p = 6.
Solution:
The demand function is x = 10 – p
Price elasticity of demand,

Price elasticity of demand when p – 6 is ηd = \(\frac{6}{10-6}=\frac{6}{4}\) = 1.5
∴ |ηd| = 1.5 > 1, the demand is elastic.
![]()
Question 16.
Find the equilibrium price and equilibrium quantity for the following functions.
Demand: x = 100 – 2p and supply: x = 3p – 50.
Solution:
Demand x = 100 – 2p
Supply x = 3p – 50
At equilibrium, demand = supply
100 – 2p = 3p – 50
-2p – 3p = -100 – 50
-5p = -150
p = \(\frac{-150}{-5}\) = 30
∴ Equilibrium price pE = 30
Supply, x = 3p – 50
Put p = 30, we get
x = 3(30) – 50 = 90 – 50 = 40
∴ Equilibrium quantity xE = 40
Question 17.
The demand and cost functions of a firm are x = 6000 – 30p and C = 72000 + 60x respectively. Find the level of output and price at which the profit is maximum.
Solution:
We know that profit is maximum when marginal Revenue (MR) = Marginal Cost (MC)
The demand function, x = 6000 – 30p
30p = 6000 – x
p = \(\frac{1}{30}\) (6000 – x)
p = \(\frac{6000}{30}-\frac{x}{30}\)
p = 200 – \(\frac{x}{30}\) …….. (1)
Revenue, R = px
= \(\left(200-\frac{x}{30}\right) x\)
= 200x – \(\frac{x^{2}}{30}\)
Marginal Revenue (MR) = \(\frac{d \mathrm{R}}{d x}\)
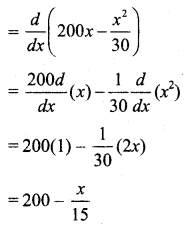
Cost function, C = 72000 + 60x
Marginal cost, \(\frac{d \mathrm{C}}{d x}\) = \(\frac{d}{d x}\) (72000 + 60x)
= 0 + 60(1)
= 60
But marginal revenue = marginal cost
200 – \(\frac{x}{15}\) = 60
\(-\frac{x}{15}\) = 60 – 200
\(-\frac{x}{15}\) = -140
-x = – 140 × 15
x = 140 × 15 = 2100
The output is 2100 units.
By (1) we have p = 200 – \(\frac{x}{30}\)
When x = 2100,
Profit, p = 200 – \(\frac{2100}{30}\) = 200 – 70 = 130
p = ₹ 130
![]()
Question 18.
The cost function of a firm is C = x3 – 12x2 + 48x. Find the level of output (x > 0) at which average cost is minimum.
Solution:
The cost function is C = x3 – 12x2 + 48x
Average cost is minimum,
When Average Cost (AC) = Marginal Cost (MC)
Cost function, C = x3 – 12x2 + 48x
Average Cost, AC = \(\frac{x^{3}-12 x^{2}+48 x}{x}\) = x2 – 12x + 48
Marginal Cost (MC) = \(\frac{d \mathrm{C}}{d x}\)
= \(\frac{d}{d x}\) (x3 – 12x2 + 48x)
= 3x2 – 24x + 48
But AC = MC
x2 – 12x + 48 = 3x2 – 24x + 48
x2 – 3x2 – 12x + 24x = 0
-2x2 + 12x = 0
Divide by -2 we get, x2 – 6x = 0
x (x – 6) = 0
x = 0 (or) x – 6 = 0
x = 0 (or) x = 6
But x > 0
∴ x = 6
Output = 6 units