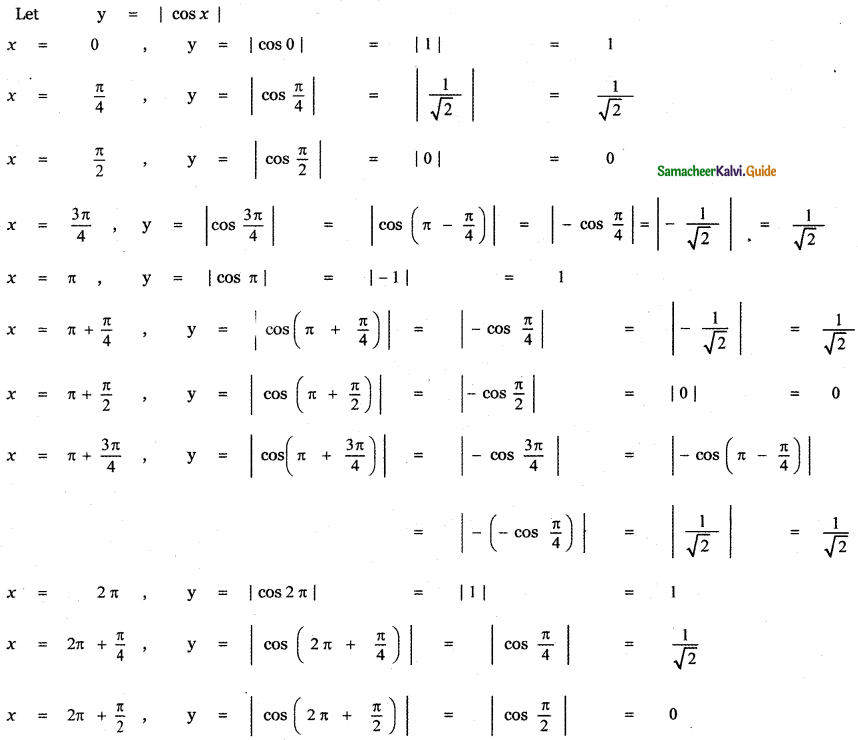Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 10 Differentiability and Methods of Differentiation Ex 10.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.1
Question 1.
Find the derivatives of the following functions using the first principle.
(i) f(x) = 6
(ii) f(x) = -4x + 7
(iii) f(x) = -x2 + 2
Answer:
(i) f(x) = 6
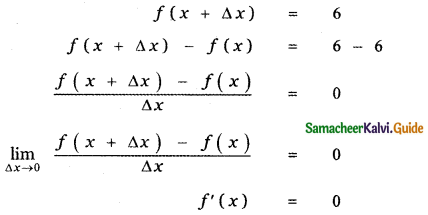
![]()
(ii) f(x) = – 4x + 7,
f(x + Δx) = -4(x + Δx) + 7
f(x + Δx) – f(x) = [-4(x + Δx) + 7] – [-4x + 7]
f(x + Δx) – f(x) = [-4(x + Δx) + 7] + 4x – 7
f(x + Δx) – f(x) = -4 Δx
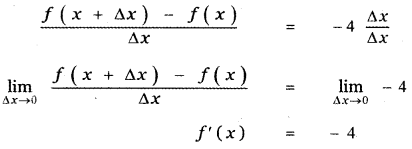
(iii) f(x) = -x2 + 2
f (x + Δx) = – (x + Δx)2 + 2
f (x + Δx) – f(x) = – [x2 + 2x Δx + (Δx)2] + 2 – [- x2 + 2]
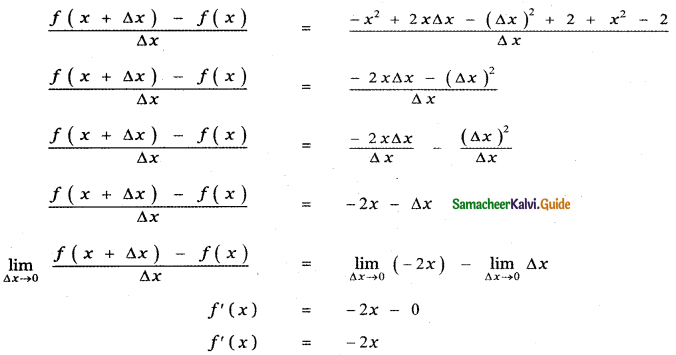
![]()
Question 2.
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
(i) f (x) = |x – 1|
Answer:
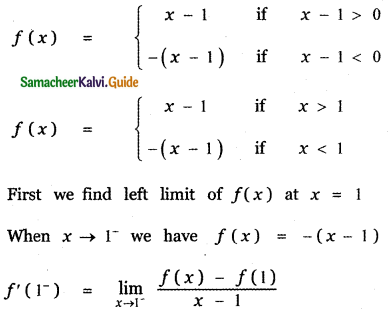
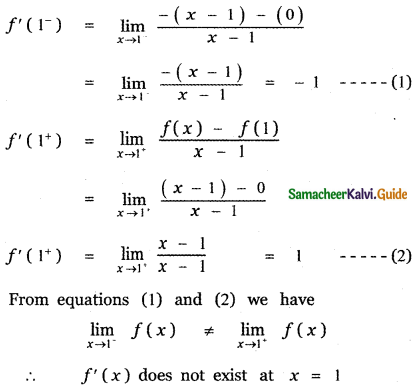
![]()
(ii) f (x) = \(\sqrt{1-x^{2}}\)
Answer:



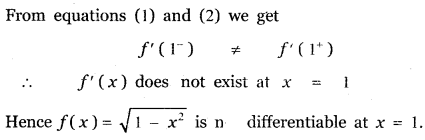
![]()
(iii) 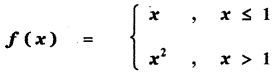
Answer:


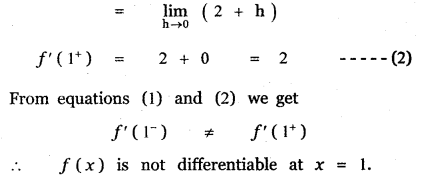
![]()
Question 3.
Determine whether the following function is differentiable at the indicated values.
(i) f(x) = x |x| at x = 0
Answer:


![]()
(ii) f(x) = |x2 – 1|at x = 1
Answer:


![]()
(iii) f(x) = |x| + |x – 1| at x = 0, 1
Answer:
To find the limit at x = 0
First we find the left limit of f(x) at x = 0
When x = 0– |x| = -x and
|x – 1| = -(x – 1)
∴ When x = 0 we have
f(x) = -x – (x – 1)
f(x) = -x – x + 1 = -2x + 1
f(0) = 2 × 0 + 1 = 1
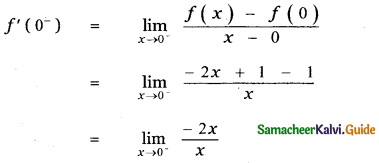
f'(0– = – 2 ……… (1)
∴When x = 0+ we have
|x| = x and |x – 1| = – (x – 1)
∴ f(x) = x – (x – 1)
f(x) = x – x + 1
f(x) = 1
f(0) = 1
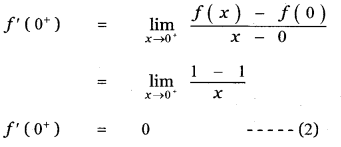
From equations (1) and (2) , we get
f'(0–) ≠ f’(0+)
∴ f(x) is not differentiable at x = 0.
To find the limit at x = 1
First we find the left limit of f (x) at x = 1
When x = 1 , |x| = x and
|x – 1| = -(x – 1)
∴ f(x) = x – (x – 1)
f(x) = x – x + 1 = 1
f(x) = 1
f(1) = 1
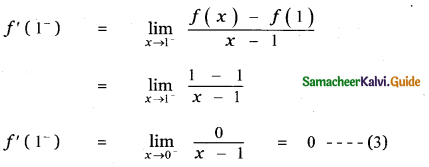
When x = 1+ , |x| = x and
|x – 1| = x – 1
When x = , |x| = x and
|x – 1| = x – 1
∴ f(x) = x + x – 1 = 2x – 1
f(1) = 2 × 1 – 1 = 2 – 1 = 1
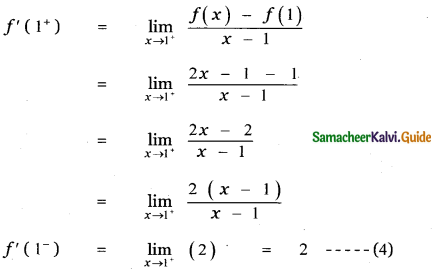
From equations (3) and (4) , we get
f’(1–) ≠ f'(1+)
∴ f (x) is not differentiable at x = 1
![]()
(iv) f(x) = sin |x| at x = 0
Answer:
First we find the left limit of f (x) at x = 0
When x = 0–, |x| = -x
∴ f(x) = sin (-x) = -sin x
f(0) = -sin 0 = 0
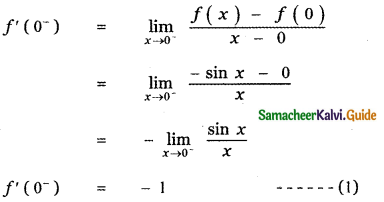
Next we find the right limit of f (x) at x = 0
When x = 0+ |x| = x
∴ f(x) = sin x
f(0) = sin 0 = 0
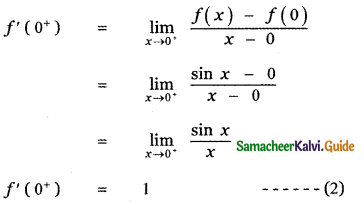
From equations (1) and (2) , we get
f’(0–) ≠ f'(0+)
∴ f (x) is not differentiable at x = 0.
![]()
Question 4.
Show that the following functions are not differentiable at the indicated value of x
(i) 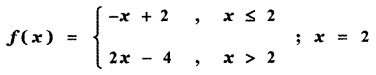
Answer:
First we find the left limit of f(x) at x = 2
When x = 2, then x ≤ 2
∴ f(x) = -x + 2
f(2) = -2 + 2 = 0
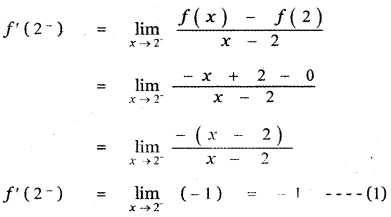
Next we find the right limit of f(x) at x = 2
When x = 2+, then x > 2
∴ f(x) = 2x – 4
f(2) = 2 × 2 – 4 = 4 – 4 = 0
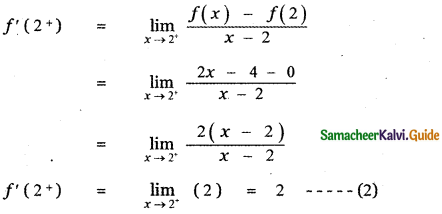
From equation (1) and (2), we get
f’(2–) ≠ f'(2+)
∴ f (x) is not differentiable at x = 2
(ii) 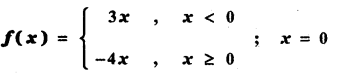
Answer:
First we find the left limit of f (x) at x = 0
When x = 0–, then x < 0
∴ f(x) = 3x
f(0) = 3 × 0 = 0
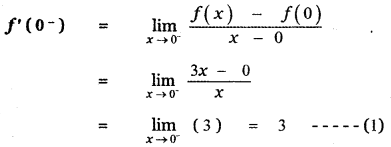
Next we find the right limit of f (x) at x = 0
When x = 0+, then x ≥ 0
∴ f(x) = -4x
f(0) = -4 × 0 = 0
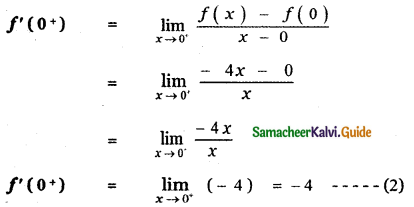
From equations (1) and (2) , we get
f'(0–) ≠ f'((0+)
∴ f (x) is not differentiable at x = 0
![]()
Question 5.
The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.
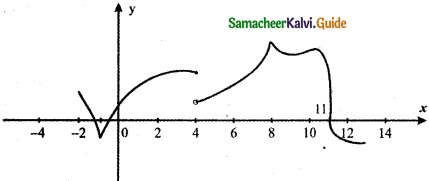
Answer:
We know A function f is not differentiable at a point x0 belonging to the domain of f if one of the following situations holds
(i) f has a vertical tangent at x0
(ii) The graph of f comes to a point at x0 (either a sharp edge ∨ or a sharp peak ∧)
For the given graph f
At x = – 1 , a sharp edge ∨
At x = 8, a sharp peak ∧
At x = 4 , discontinuity
At x = 11, perpendicular tangent
∴ The given graph is not differentiable at
x = – 1, 8, 4, 11
Question 6.
If f(x) = |x + 100| + x2, test whether f’(-100) exists.
Answer:
f(x) = |x + 100| + x2
First let us find the left limit of f( x) at x = – 1100
When x < – 100 ,
f(x) = – (x + 100) + x2
f(- 100) = – (- 100 + 100) + (- 100)2
f(- 100) = 1002
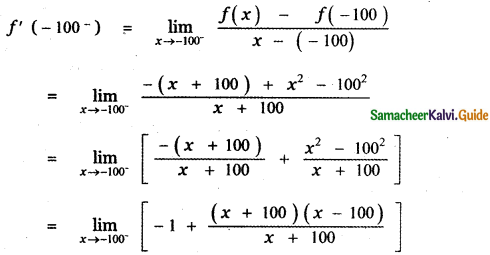
![]()
= -1 – 100 – 100
f’ (-100) = -201 ——– (1)
Next let us find the right limit of f( x) at x = -100
when x > – 100
f(x) = x + 100 + x2
f(- 100) = – 100 + 100 + (- 100)2
f(- 100) = 1002
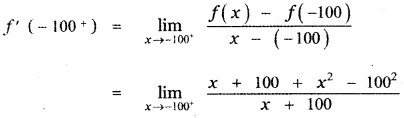
f'(-100+) = – 199 ……… (2)
From equation (1) and (2) , we get
f’(- 100–) ≠ f'(- 100+)
∴ f’ (x) does not exist at x = -100
Hence, f'(- 100) does not exist
![]()
Question 7.
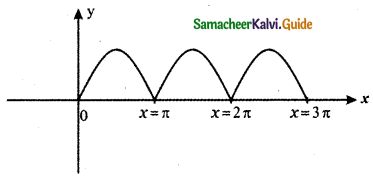
Examine the differentiability of functions in R by drawing the diagrams. (i) |sin x| (ii) |cos x|
(i) |sin x|
Answer:


At the points, x = 0, π, 2π, 3π, ……….. the graph of the given function has a sharp edge V.
∴ At these points, the function is not differentiable.
∴ The function y = |sin x| is not differentiable at
x = nπ, for all n ∈ Z.
![]()
(ii) |cos x|
Answer: