Samacheer Kalvi 11th Maths Guide Chapter 12 Introduction to Probability Theory Ex 12.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 12 Introduction to Probability Theory Ex 12.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.1

Question 1.
An experiment has the four possible mutually exclusive and exhaustive outcomes A, B, C, and D. Check whether the following assignments of probability are permissible.
(i) P (A) = 0.15, P (B) = 0.30,
P (C) = 0.43, P (D) = 0.12
Answer:
P(A) = 0.15, P(B) = 0.30, P(C) = 0.43, P(D) = 0.12
Now P(A) + P(B) + P(C) + P(D) = 0.15 + 0.30 + 0.43 + 0.12 = 1
0.15 + 0.30 + 0.43 + 0.12 = 1
∴ The assignment of probability is permissible.

(ii) P (A) = 0.22, P (B) = 0.38,
P (C) = 0.16, P (D) = 0.34
Answer:
Given that
P (A) = 0.22 ≥ 0,
P (B) = 0.38 ≥ 0,
P(C) = 0.16 ≥ 0 ,
P (D) = 0.34 ≥ 0
P(S) = P (A) + P(B) + P(C) + P(D)
= 0.22 + 0.38 + 0.16 + 0.34
= 1.1 > 1
Therefore the assignment of probability isn’t permissible

(iii) P(A) = \(\frac{2}{5}\), P(B) = \(\frac{3}{5}\),
P(C) = – \(\frac{1}{5}\), P(D) = \(\frac{1}{5}\)
Answer:
P(A) = \(\frac{2}{5}\), P(B) = \(\frac{3}{5}\), P(C) = \(-\frac{1}{5}\), P(D) = \(\frac{1}{5}\)
P(C) = \(-\frac{1}{5}\) which is not possible
(i.e.) for any event A, (0 ≤ P(A) ≤ 1)
∴ The assignment of probability is not permissible.

Question 2.
If two coins are tossed simultaneously, then find the probability of getting
(i) one head and one tail
(ii) at most two tails
Answer:
Two coins are tossed simultaneously = one coin is tossed two times.
The sample space S = { H , T } × { H , T }
S = {HH, HT, TH, TT }
n(S) = 4
Let A be the event of getting one head and one tail, B be the event of getting atmost two tails.
A = {HT, TH}
n(A) = 2
B = {HH, HT , TH, TT}
n (B) = 4

(i) P (getting one head and one tail)

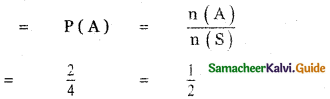
(ii) P (getting atmost two tails)

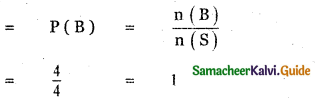
Question 3.
Five mangoes and 4 apples are in a box. If two fruits are chosen at random, find the probability that
(i) one is a mango and the other is an apple
(ii) both are of the same variety.
Answer:
(i) One is a mango and the other is an apple:
Let S be the sample space, A be the event of taking one mango and one apple.
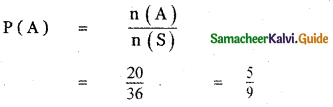
n(S) = 9C₂
n (A) = 5C₁ × 4C₁
= 5 × 4 = 20

(ii) Both are of the same variety:
Let S be the sample space, A be the event of taking 2 mangoes and B be the event of taking 2 apples
∴ n(s) = 9C₂

P(taking 2 fruits are of the same colour)
= P(A or B)
= P(A ∪ B)
= P(A) + P(B)

Question 4.
What is the chance that
(i) Non – leap year
Answer:
Non-leap year
No of days = 365
= \(\frac{365}{7}\) weeks = 52 weeks + 1 day
In 52 weeks we have 52 Sundays. So we have to find the probability of getting the remaining one day as Sunday. The remaining 1 day can be Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday
(i.e.,) n(S) = 7
In the n (Sunday) = A {Saturday to Sunday or Sunday to Monday}
(i.e.,) n(A) = 1
So, P(A) = 1.
∴ Probability of getting 53 Sundays \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{1}{7}\)

(ii) Leap year should have fifty-three Sundays?
Answer:
In 52 weeks we have 52 Sundays. We have to find the probability of getting one Sunday to form the remaining 2 days can be a combination of the following S = {Saturday to Sunday, Sunday to Monday, Monday, to Tuesday, Tuesday to wednes¬day, Wednesday to Thursday, Thursday to Friday, Friday and Saturday}.
(i.e) n(s) =7
In this = A {Saturday to Sunday, Sunday to Monday}
(i.e) n(A) = 2
So, P(A) = \(\frac{2}{7}\)

Question 5.
Eight coins are tossed once, find the probability of getting
(i) exactly two tails
(ii) at least two tails
(iii) at most two tails
Answer:
Eight coins are tossed simultaneously one time = one coin is tossed eight times.
Let S be the sample space.
S = {H, T} × {H, T} × ………….. × {H, T} 8 times
Let A be the event of getting exactly two heads,
B be the event of getting atleast two tails and
C be the event of getting atmost two tails.
When eight coins are tossed, the number of elements in the sample space
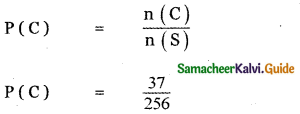
n(S) = 2⁸ = 256
n(A) = 8C₂
= \(\frac{8 \times 7}{1 \times 2}\) = 28
n (B) = 8C₂ + 8C₃ + 8C₄ + 8C₅ + 8C₆ + 8C₇ + 8C₈
= n (S) – (8C₈ + 8C₁)
= n (S) – {n (Event of getting all heads) + n (Event of getting one head)}
= n(S) – (1 + 8)
= 256 – 9 = 247
n (C) = 8C₀ + 8 C₁ + 8 C₂
= 1 + 8 + \(\frac{8 \times 7}{1 \times 2}\)
= 1 + 8 + 28 = 37

(i) P {getting exactly two tails) =

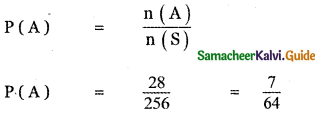
(ii) P (getting atleast two tails ) =

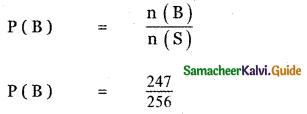
(iii) P (getting atmost two tails) =

Question 6.
An integer is chosen at random from the first 100 positive integers. What is the probability that the integer chosen is a prime or multiple of 8 ?
Answer:
Let S be the sample space
S = { 1, 2, 3, …………., 100 }
Let A be the event of choosing a prime number
A = { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}
n(A) = 25
Let B be the event of choosing an integer a multiple of 8.
B = { 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96}
n(B) = 12
P(Choosing a prime number) = P(A)

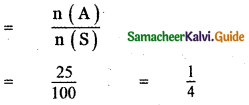
P (Choosing an integer a multiple of 8) = P (B)

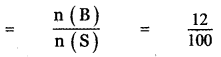
P ( Choosing an integer a prime or multiple of 8)
= P(A or B)
= P(A ∪ B)
P(A) + P(B)
(since A and B are mutually exclusive that is A ∩ B = Φ)

Question 7.
A bag contains 7 red 4 black balls, 3 balls are drawn at random. Find the probability that
(i) all are red
(ii) one red and 2 black.
Answer:
Let S be the sample space, A be the event of taking 3 red balls and B be the event of taking one red and
2 black balls.
A bag contains 7 red balls and 3 black balls.
3 balls are drawn at random.
∴ The number of outcomes n(S) = 11C₃
= \(\frac{11 \times 10 \times 9}{1 \times 2 \times 3}\)
= 11 × 5 × 3 = 165

n (A) = 7C₃

n(B) = 7C₁ × 4C₂
= 7 × \(\frac{4 \times 3}{1 \times 2}\) = 7 × 6 = 42

(i) p (getting 3 red balls) = p(A)

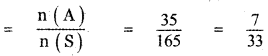
(ii) p (getting one red and 2 blacks) = p(B)

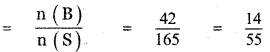
Question 8.
A single card is drawn from a pack of 52 cards. What is the probability that
(i) the card is an ace or a king
(ii) the card w11 be 6 or smaller
(iii) the card is either a queen or 9?
Answer:
S be the sample space one card is drawn from a pack of 52 cards.
∴ n(S) = 52C₁
n(S) = 52

(i) The card is an ace or a king
Let A be the event of getting an ace.
n(A) = 4C₁ = 4
Let B be the event of getting a king.
n(B) = 4C₁ = 4
P (getting an ace or a king)
= P(A or B)
= P(A ∪ B)
= P(A) + P(B)
(since A and B are mutually exclusive events, A ∩ B = Φ)

(ii) The card will be 6 or smaller:
Let A be the event of getting a number 6.
∴ n(A) = 4C₁ = 4
Let B be the event of getting numbers less than 6.
n(B) = 16C₁ = 16
P (the card will be 6 or less than 6)
= P(A or B)
= P(A ∪ B)
= P(A) + P(B)
(since A and B are mutually exclusive events A ∩ B = Φ)

(iii) The card is either a queen or 9?
Let A be the event of getting a Queen.
∴ n(A) = 4C₁ = 4
Let B be the event of getting a number 9.
n(B) = 4C₁ = 4
P (the card is either a Queen or 9)
= P(A or B)
= P(A ∪ B
= P(A) + P(B)
(since A and B are mutually exclusive events)

Question 9.
A cricket club has 16 members, of whom only 5 can bowl. What is the probability that in a team of 11 members at least 3 bowlers are selected?
Answer:
Number of members in the cricket club = 16
Number of bowlers = 5
Number of batters = 16 – 5 = 11
The probability that a team of 11 members consisting of atleast 3 bowlers = (Probability of selecting 3 bowlers and 8 batters) + ( Probability of selecting 4 bowlers and 7 batters) + (Probability of selecting 5 bowlers and 6 batters)
The probability that a team of 11 members consisting of atleast 3 bowlers

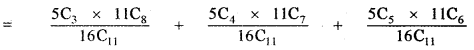
[Selection procedure:
First out of total 16 members selecting 11 members in 16C₁₁ ways.
Selection of 11 members consisting minimum of 3 bowlers.
∴ Selection of 11 members as follows
(1) 3 bowlers from 5 bowlers and 8 batters from 11 batters.
(2) 4 bowlers from 5 bowlers and 7 batters from 11 batters.
(3) 5 bowlers from 5 bowlers and 6 batters from 11 batters.]

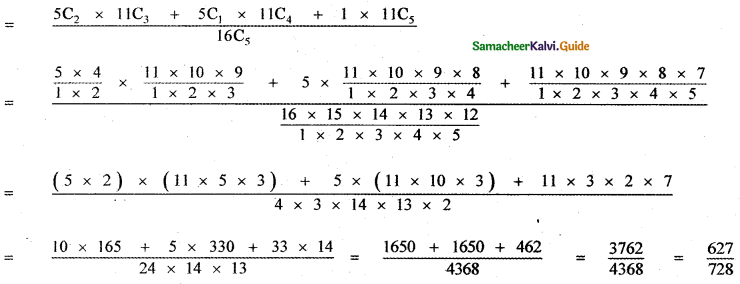
Question 10.
(i) The odds that event A occurs is 5 to 7, find P(A).
Answer:
Given the odds, that event A occurs is 5 to 7.

(ii) Suppose p (B) = \(\frac{2}{5}\). Express the odds that the event B occurs.
Answer:

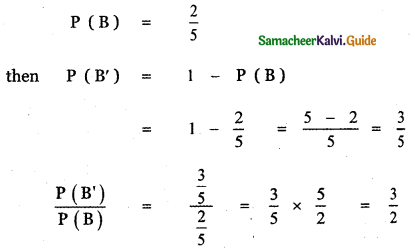
∴ The odds that the event B occurs is 2 to 3.