Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.3
Question 1.
Represent the following inequalities in the interval notation:
(i) x ≥ – 1 and x < 4
Answer:
x ≥ – 1 and x < 4
x ∈ [- 1, 4)
![]()
(ii) x ≤ 5 and x ≥ – 3
Answer:
x ≤ 5 and x ≥ – 3
– 3 ≤ x ≤ 5
∴ x ∈ [- 3, 5 ]
(iii) x < – 1 or x < 3
Answer:
x < – 1 or x < 3
x ∈ (-∞, 3)
(iv) -2x > 0 or 3x – 4 < 11
Answer:
– 2x > 0 or 3x – 4 < 11
2x < 0 or 3x < 11 + 4
x < 0 or x < \(\frac{15}{3}\)
x < 0 or x < 5
x ∈ (- ∞, 5)
![]()
Question 2.
Solve 23x < 100 when
(i) x is a natural number,
(ii) x is an integer.
Answer:
Given 23x < 100
(i) When x is a natural number
23x < 100
⇒ x < \(\frac{100}{23}\)
⇒ x < 4.347
⇒ x = 1, 2, 3, 4
∴ The solution set is { 1, 2, 3 , 4 }
(ii) When x is an integer
23x < 100
⇒ x < \(\frac{100}{23}\)
⇒ x < 4.347
⇒ x = …… , – 3, – 2, – 1, 0, 1, 2, 3, 4
Hence the solution set is
{ ………, – 3, – 2, – 1, 0, 1 , 2 , 3 , 4 }
![]()
Question 3.
Solve – 2x ≥ 9 when
(i) x is a real number,
(ii) x is an integer
(iii) x is a natural number.
Answer:
Given – 2x ≥ 9
⇒ – x ≥ \(\frac{9}{2}\)
⇒ x ≤ \(-\frac{9}{2}\)
(i) When x is a real number
x ≤ \(-\frac{9}{2}\)
The solution set is \(\left(-\infty,-\frac{9}{2}\right]\)
(ii) x is an integer
x ≤ –\(-\frac{9}{2}\)
x ≤ – 4.5
x = …………., -7, – 6, -5
(iii) x is a natural number
x ≤ – \(\frac{9}{2}\)
x ≤ – 4.5
Since there exists no natural number less than – \(\frac{9}{2}\)
∴ No solution
![]()
Question 4.
Solve:
(i) 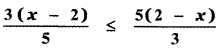
Answer:
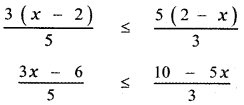
3 (3x – 6) ≤ 5 (10 – 5x)
9x – 18 ≤ 50 – 25 x
9x + 25 x ≤ 50 + 18
34x ≤ 68
x ≤ \(\frac{68}{34}\) = 2
x ≤ 2
∴ The solution set is (-∞, 2]
![]()
(ii) ![]()
Answer:
![]()
Multiplying both sides by 3, we have
5 – x < \(\frac{3 x}{2}\) – 12
Multiplying both sides by 2, we have
10 – 2x < 3x – 24
10 + 24 < 3x + 2x
34 < 5x
\(\frac{34}{5}\) < x
x > \(\frac{34}{5}\)
∴ The solution set is \(\left(\frac{34}{5}, \infty\right)\)
![]()
Question 5.
To secure an A grade, one must obtain an average of 90 marks or more in 5 subjects each of a maximum of 100 marks. If one scored 84, 87, 95, 91 in the first four subjects, what is the minimum mark one scored in the fifth subject to get an A grade in the course?
Answer:
Required marks = 5 × 90 = 450
Total marks obtained in 4 subjects = 84 + 87 + 95 + 91 = 357
So required marks in the fifth subject = 450 – 357 = 93
Question 6.
A manufacturer has 600 litres of a 12 percent solution of acid. How many litres of a 30 percent acid solution must be added to it so that the acid content in the resulting mixture will be more than 15 percent but less than 18 percent?
Answer:
Amount of 12% solution of acid = 600 litres
Let x be the required number litres of 30 % acid solution to be added to the given 600 litres of 12 % acid solution to make the resulting mixture will be more than 15 % but less than 18 %.
∴ Total amount of mixture = (600 + x) litres
30% acid solution of x litres + 12% acid solution of 600 litres > 15% acid solution of (600 + x) litres
\(\frac{30}{100}\) × x + \(\frac{12}{100}\) × 600 > \(\frac{15}{100}\) × (600 + x)
30x + 7200 > 9000 + 15x
30x – 15x > 9000 – 7200
15x > 1800
x > \(\frac{1800}{15}\) = 120
x > 120 ——– (1)
Also 30% acid solution of x litres + 12% acid solution of 600 litres < 18% acid solution of ( 600 + x) litres.
\(\frac{30}{100}\) × x + \(\frac{12}{100}\) × 600 < \(\frac{15}{100}\) × (600 + x)
30x + 7200 < 18 (600 + x)
30x + 7200 < 10800 + 18x
30x – 18x < 10,800 – 7200
12x < 3600
x < \(\frac{3600}{12}\) = 300
x < 300 ——- (2)
From equations (1) and (2), we get ) 120 < x < 300
∴ The numbers of litres of the 30% acid solution to be added is greater than 120 litres and less than 300 litres.
![]()
Question 7.
Find all pairs of consecutive odd natural numbers both of which are larger than 10 and their sum is less than 40.
Answer:
Let x and x + 2 be the two pair of consecutive odd natural numbers.
Given x > 10 ——— (1)
and x + 2 > 10 ——— (2)
Also x + (x + 2) < 40 ——— (3)
From equations (1), we have
x = 11, 13 , 15, 17, 19, 21 …………
Using equation (3), the required pairs are
(11, 13), (13, 15), (15, 17), ( 17, 19), (19 ,21 ) is not possible since 19 + 21 = 40
Question 8.
A model rocket is launched from the ground. The height h reached by the rocket after t seconds from lift off is given by h(t) = – 5t2 + 100t, 0 ≤ t ≤ 20. At what times, the rocket is 495 feet above the ground?
Answer:
h(t) = -5t2 + 100t
at t = 0, h(0) = 0
at t = 1, h(1) = -5 + 100 = 95
at t = 2, h(2) = -20 + 200 = 180
at t =3, h(3) = -45 + 300 = 255
at t = 4, h(4) = -80 + 400 = 320
at t = 5, h(5) = -125 + 500 = 375
at t = 6, h(6) = – 180 + 600 = 420
at t = 7, h(7) = -245 + 700 = 455
at t = 8, h(8) = – 320 + 800 = 480
at t = 9, h(9) = -405 + 900 = 495
So, at 9 secs, the rocket is 495 feet above the ground.
![]()
Question 9.
A plumber can be paid according to the following schemes: In the first scheme he will be paid rupees 500 plus rupees 70 per hour and in the second scheme, he will pay rupees 120 per hour. If he works x hours, then for what value of x does the first scheme give better wages?
Answer:
I scheme with x hr
500 + (x- 1) 70 = 500 + 70x – 70 = 430 + 70x
II scheme with x hours
120x
Here I > II
⇒ 430 + 70x > 120x
⇒ 120x – 70x < 430
50x < 430
\(\frac{50 x}{50}<\frac{430}{50}\)
x < 8.6 (i.e.) when x is less than 9 hrs the first scheme gives better wages.
![]()
Question 10.
A and B are working on similar jobs but their monthly salaries differ by more than Rs. 6000. If B earns rupees 27,000 per month, then what are the possibilities of A’s salary per month?
Answer:
A’s monthly salary = ₹ x
B’s monthly salary = ₹ 27000
Their annual salaries differ by ₹ 6000
A’s salary – 27000 > 6000
A’s salary > ₹ 33000
B’s salary – A’s salary > 6000
27000 – A’s salary > 6000
A’s salary < ₹ 21000
A’s monthly salary will be lesser than ₹ 21,000 or greater than ₹ 33,000