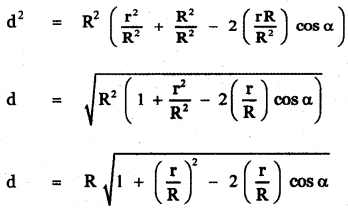Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.10 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.10
Question 1.
Determine whether the following measurements produce one triangle, two triangles or no triangle. ∠B = 88°, a = 23 , b = 2. Solve if solution exists.
Answer:
Using sine formula
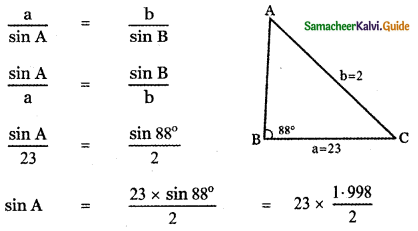
= 23 × 0.999
= 22.99
which is not possible
∴ Solution of the given triangle does not exsit.
![]()
Question 2.
If the sides of a ∆ ABC are a = 4, b = 6 and C = 8, then show that 4 cos B + 3 cos C = 2.
Answer:
In ∆ ABC Given that a = 4, b = 6, c = 8
Using cosine formula
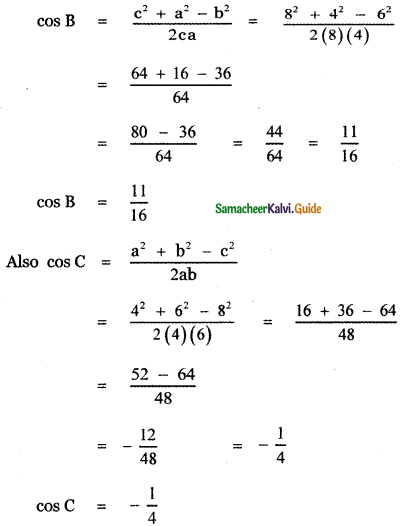
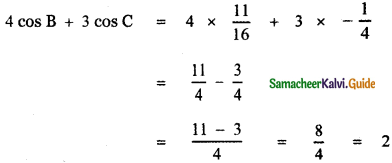
![]()
Question 3.
In a ∆ ABC, if a = √3 – 1, b = √3 + 1 and C = 60° find the other side and other two angles.
Answer:
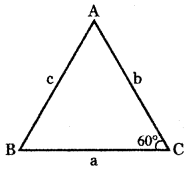
In a ∆ ABC, Given
a = √3 – 1, b = √3 + 1
C = 60°
Using cosine formula a
C2 = a2 + b2 – 2 ab cos C
= (√3 – 1)2 + (√3 + 1)2 – 2(√3 – 1) × (√3 + 1) cos 6o°
= 3 – 2√3 + 1 + 3 + 2√3 + 1 – 2 (3 – 1) × \(\frac { 1 }{ 2 }\)
c2 = 8 – 2 = 6 ⇒ c = √6
Using sine formula
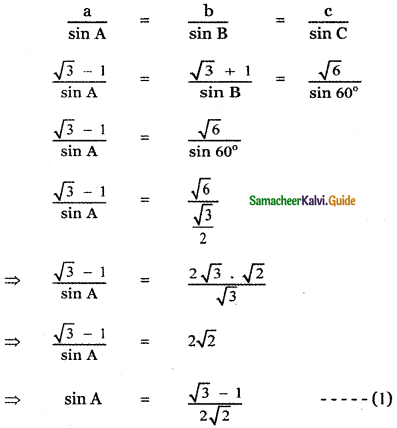
sin (45° – 30°) = sin 45° . cos 30° – cos 45° sin 30°
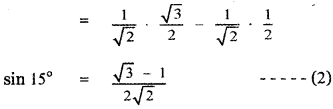
From equations (1) and (2), we have
sin A = sin 15° ⇒ A = 15°
In ∆ ABC, we have A + B + C = 180°
15° + B + 60° = 180°
B = 180°- 75°
B = 105°
∴ The required sides and angles are
c = √6, A = 15°, B = 105°
![]()
Question 4.
In any ∆ ABC, prove that the area
![]()
Answer:
Area of ∆ ABC is ∆ = \(\frac { 1 }{ 2 }\) bc = sin A
Using cosine formula
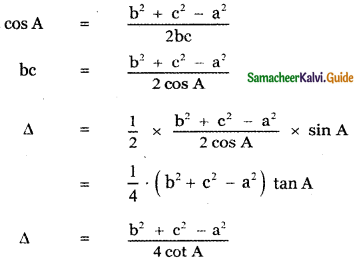
Question 5.
In a ∆ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm.
Answer:
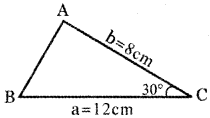
In ∆ ABC Given
a = 12 cm ,
b = 8 cm,
C = 30°

![]()
Question 6.
In a ∆ABC, if a = 18 cm, b = 24 cm and c = 30 cm, then show that its area is 216 sq.cm.
Answer:
In a ∆ ABC, Given a = 18 cm, b = 24cm and c = 30 cm
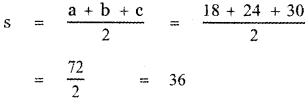
Area of the triangle ABC

Question 7.
Two soldiers A and B in two different underground bunkers on a straighi road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5km apart, find the distance of the intruder from B.
Answer:
Let A and B be the two positions of the soldiers.
AC – direction of the intruder seen from A.
BC – the direction of the intruder seen from B.
∠ BAC = 30° angle of elevation of the intruder from A.
∠ PBC = 45° angle of elevation of the intruder from B.
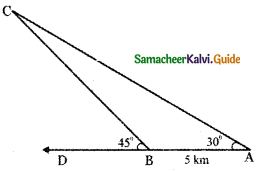
Distance between A and B = 5k.m.
In ∆ ABC, ∠ ABC = 180° – 45° = 135°
∠ BCA = 180° – ( 135° + 30°)
= 180° – 165° = 15°
Using sine formula

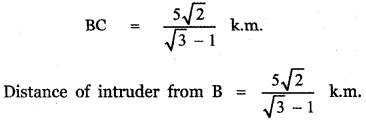
![]()
Question 8.
A researcher wants to determine the width of a pond from east to west, which cannot be done by actual measurement. From a point P, he finds the distance to the eastern-most point of the pond to be 8 km, while the distance to the westernmost point from P to be 6 km. If the angle between the two lines of sight is 60°, find the width of the pond.
Answer:
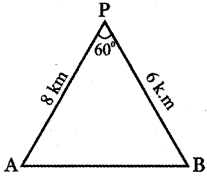
A – be the easternmost point on the pond and
B – be the westernmost point on the pond.
AB – Width of the pond
P – Point of observation.
The distance of A from P = 8 km
Distance of B from P = 6km
Angle between the directions PA and PB
∠APB = 60°
In ∆ PAB, using cosine formula
AB2 = PA2 + PB2 – 2PA . PB . cos ∠APB
AB2 = 82 + 62 – 2 × 8 × 6 . cos 60°
= 64 + 36 – 96 × \(\frac { 1 }{ 2 }\)
= 100 – 48 = 52
AB = \(\sqrt{52}\) = \(\sqrt{4 \times 13}\)
AB = 2\(\sqrt{13}\) k.m.
Width of the pond = 2\(\sqrt{13}\) k.m
![]()
Question 9.
Two Navy helicopters A and B are flying over the Bay of Bengal at saine altitude from sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends 60° at the boat, find the distance of the boat from B.
Answer:
A , B are the positions of the helicopter above the sea level.
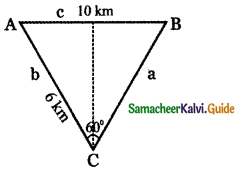
Distance between A and B = 10 km
C – Position of the boat on the surface of sea.
AC, BC are the directions of the boat as seen from A and B respectively.
Distance of the boat C from A = 6 k.m
∠ ACB = 60°
Using cosine formula
AB2 = BC2 + AC2 – 2 BC . AC cos ∠ACB
c2 = a2 + b2 – 2 ab cos C
102 = a2 + 62 – 2a × 6 cos 60°
100 = a2 + 36 – 12a\(\left(\frac{1}{2}\right)\)
0 = a2 + 36 – 6a – 100
a2 – 6a – 64 = 0
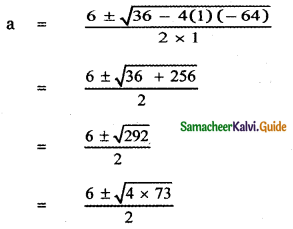

![]()
Question 10.
A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3 km, BP = 5 km, and ∠APB = 120°, then find the length of the tunnel to be built.
Answer:
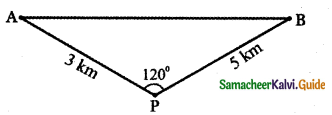
p2 = a2 + b2 – 2ab cos P
p2 = 9 + 25 – 30 Cos 120°
p2 = 9 + 25 – 30 (-1/2) = 34 + 15 = 49
⇒ p = \(\sqrt{49}\) = 7 km
![]()
Question 11.
A farmer wants to purchase a triangular-shaped land with sides 120 feet and 60 feet and the angle included between these two sides is 60°. If the land costs Rs.500 per square feet, find the amount he needed to purchase the land. Also, find the perimeter of the land.
Answer:
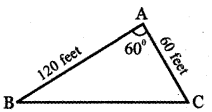
Let ∆ ABC be the shape of the land.
Given AB = 120 ft, AC = 60ft
∠ BAC = 60°
Using cosine formula in ∆ ABC
BC2 = AB2 + AC2 – 2AB . AC cos ¿BAC
BC2 = 1202 + 602 – 2 × 120 × 60 cos (60°)
= 14400 + 3600 – 14400 × \(\frac { 1 }{ 2 }\)
= 18000 – 7200
BC2 = 10800 = 100 × 2 × 2 × 3 × 3 × 3
BC2 = 102 × 22 × 32 × 3
BC = \(\sqrt{10^{2} \times 2^{2} \times 3^{2} \times 3}\)
BC = 10 × 2 × 3√3
BC = 60√3 k.m.
Perimeter of the Land = AB + BC + AC
= 120 + 60√3 + 60
= 180 + 60√3
= 60 (3 + √3) feet.
Area of ∆ ABC = \(\frac { 1 }{ 2 }\) × AB × AC × sin ∠ BAC
= \(\frac { 1 }{ 2 }\) × 60 × 120 sin 60°
= 30 × 120 × \(\frac{\sqrt{3}}{2}\)
= 30 × 60 × √3
= 1800 √3 sq. feet.
Cost of 1 sq. feet Rs. 500
∴ Cost of 800 √3 sq. feet = 800 √3 × 500 = 900000√3
Total amount needed = Rs. 900000√3
Perimeter of the land = 60(3 + √3)feet.
![]()
Question 12.
A fighter jet has to hit a small target by flying a horizontal distance. When the target is sighted, the pilot measures the angle of depression to be 30°. If after 100 km, the target has an angle of depression of 45°, how far is the target from the fighter jet at that instant?
Answer:
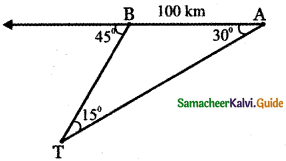
Let A be the position of the jet fighter observing the target at an angle of depression 30°.
Also, Let B be the position of the jet 100 k.m away horizontally from A observing the target at an angle of depression 45°.
In ∆ TAB, AB = 100 k.m
∠TAB = 30°
∠ABT = 180°- 45° = 135°
∠ATB = 180° – (135°+ 300) = 180° – 165° = 15°
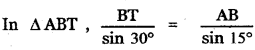

![]()
Question 13.
A plane is 1 km from one landmark and 2 km from another. From the plane’s point of view, the land between them subtends an angle of 45°. How far apart are the landmarks?
Answer:
A, B are the two landmarks,
C – Position of the plane.
The distance of the plane from the landmark A = 1 k.m
The distance of the plane from the landmark B = 2 k.m
∠ACB = 45°
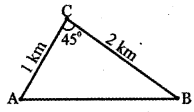
From the ∆ ABC, using cosine formula
AB2 = AC2 + BC2 – 2AC. BC. cos45°
= 12 + 22 – 2 × 1 × 2
AB2 = 1 + 4 – 2 × √2 = 5 – 2√2
AB = \(\sqrt{5-2 \sqrt{2}}\)
Distance between the landmarks AB = \(\sqrt{5-2 \sqrt{2}}\) km.
![]()
Question 14.
A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A = 60° and ∠B = 45°, AC = 4km in the ∆ ABC. Find the total distance he covered during his morning walk.
Answer:
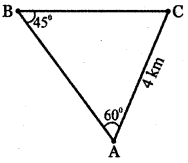
Given In ∆ABC
AC = 4 k.m
∠A = 60°,
∠B = 45°
∠C = 180° – (60° + 45°)
∴ ∠C = 180° – 105° = 75°
Using sine formula

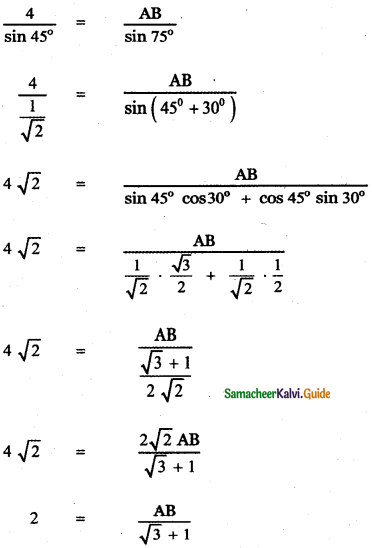

![]()
Question 15.
Two vehicles leave the same place P at the same time moving along two different roads. One vehicle moves at an average speed of 60 km/hr and the other vehicle moves at an average speed of 80 km/hr. After half an hour the vehicle reaches destinations A and B. If AB subtends 60° at the initial point P, then find AB.
Answer:
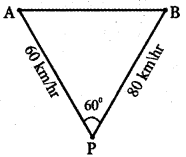
P – Initial point.
PA – The direction of the first vehicle travels with speed km/hr.
PB – The direction of the second vehicle travels with a speed of 80km/hr.
Given in half an hour first vehicle reaches destination A.
∴ PA = \(\frac{60}{2}\) = 30 km.
Also in half an hour the second vehicle reaches the destination B.
∴ PA = \(\frac{80}{2}\) = km.
In ∆ PAB, PA = 30, PB = 40, ∠APB = 60°
Using cosine formula
AB2 = PA2 + PB2 – 2PA PB cos ∠APB
AB = 302 + 402 – 2 × 30 × 40 cos 60°
= 900 + 1600 – 2400 × \(\frac { 1 }{ 2 }\)
= 2500 – 1200
AB2 = 1300
AB = \(\sqrt{1300}\) = \(\sqrt{13 \times 100}\)
AB = 10√13 k.m.
![]()
Question 16.
Suppose that a satellite in space, an earth station, and the centre of earth all lie in the same plane. Let r be the radius of earth and R he the distance from the centre of earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30° be the angle of elevation from the earth station to the satellite, If the line segment connecting the earth station and satellite subtends angle α at the centre of earth then prove that
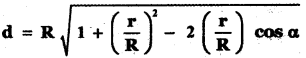
Answer:
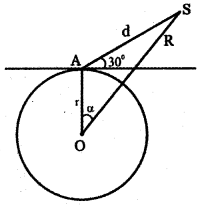
O – Centre of Earth,
A – Position of Earth station.
S – Position of the satellite.
Given the radius of Earth
OA = r
The angle of elevation of the satellite from the Earth station = 30°
The distance of the satellite from the Earth station AS = d
The distance of the satellite from the centre of the Earth OS = R.
Angle subtended by the line segment AS at the centre of earth ∠AOS = α
In △ AOS, OA = r, AS = d, OS = R, ∠AOS = α
Using cosine formula
AS2 = OA2 + OS2 – 2 OA . OS cos ∠AOS
d2 = r2 + R2 – 2(r) (R) cos α