Samacheer Kalvi 11th Maths Guide Chapter 4 Combinatorics and Mathematical Induction Ex 4.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 Combinatorics and Mathematical Induction Ex 4.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4

Question 1.
By the principle of mathematical induction, prove that, for n ≥ 1
1² + 2² + 3² + ……….. + n³ = \(\left(\frac{\mathbf{n}(\mathbf{n}+\mathbf{1})}{2}\right)^{2}\)
Answer:
Let P(n) = 1² + 2² + 3² + ……….. + n³
p(n) = \(\left(\frac{\mathbf{n}(\mathbf{n}+\mathbf{1})}{2}\right)^{2}\)

Step 1:
Let us verify the statement for n = 1
p(1) = 1³ = \(\left(\frac{1(1+1)}{2}\right)^{2}\)

P(1) = 1
∴ The given statement is true for n = 1

Step 2 :
Let us assume that the given statement is true for n = k
P(k) = 1³ + 2³ + 3³ + …………… + k³

Step 3 :
Let us prove the statement is true for n = k + 1
P(k + 1 ) = 1³ + 2³ + 3³ + …………… + k³ + (k + 1)³

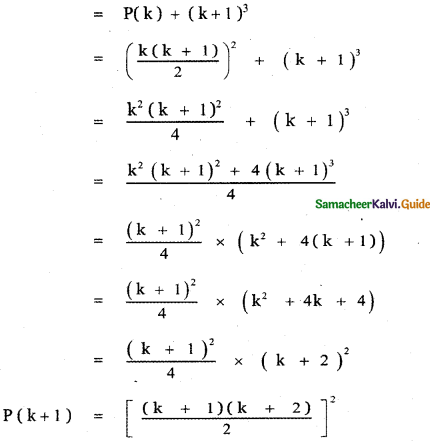
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
1² + 2² + 3² + ……….. + n³ = \(\left(\frac{\mathbf{n}(\mathbf{n}+\mathbf{1})}{2}\right)^{2}\)
is true for all natural numbers n.

Question 2.
By the principle of mathematical induction, prove that, for n ≥ 1

Answer:

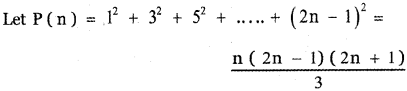
Step 1 :
Let us verify the statement for n = 1

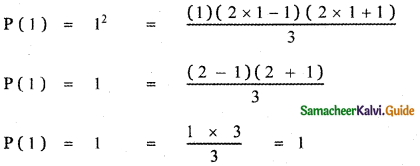
∴ The given statement is true for n = 1

Step 2 :
Let us assume that the given statement is true for n = k

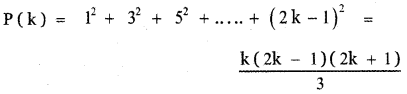
Step 3:
Let us prove the statement is true for n = k + 1


This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

is true for all natural numbers n.

Question 3.
Prove that the sum of the first ’n’ non-zero even numbers is n² + n.
Answer:
Let P(n) : 2 + 4 + 6 +…+2n = n² + n, ∀ n ∈ N

Step 1:
P( 1) : 2 = 1² + 1 = 2 which is true for P( 1)

Step 2:
P(k): 2 + 4 + 6+ …+ 2k = k² + k. Let it be true.

Step 3:
P(k + 1) : 2 + 4 + 6 + … + 2k + (2k + 2)
= k²+ k + (2k + 2) = k² + 3k + 2
= k² + 2k + k + 1 + 1
= (k+ 1)²+ (k + 1)
Which is true for P(k + 1)
So, P(k + 1) is true whenever P(k) is true.

Question 4.
By the principle of mathematical induction, prove that, for n ≥ 1, 1 . 2 + 2 . 3 + 3 . 4 + …………. + n . (n + 1) = \(\frac{\mathbf{n}(\mathbf{n}+1)(\mathbf{n}+2)}{3}\)
Answer:
Let P(n) = 1 . 2 + 2 . 3 + 3 . 4 + ………… + n . (n + 1) = \(\frac{\mathbf{n}(\mathbf{n}+1)(\mathbf{n}+2)}{3}\)

Step 1:
Let us verify the statement for n = 1
P(1) = 1 . 2 = \(\frac{1(1+1)(1+2)}{3}\)
= 1 . 2 = \(\frac{1 \cdot 2 \cdot 3}{3}\)
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k
P (k) = 1-2 + 2-3 + 3- 4 + + k (k + 1 ) =

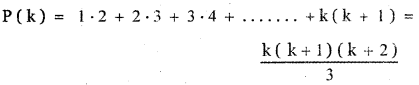
Step 3:
Let us prove the result for n = k + 1
P(k + 1) = 1 . 2 + 2 . 3 + 3 . 4 + …………… + k (k + 1) (k + 1) (k + 1 + 1)
P (k + 1) = 1 . 2 + 2 . 3 + 3 . 4 + ………….. + k (k + 1) + (k + 1 ) (k + 2)
P (k + 1 ) = P(k) + (k + 1) (k + 2)

This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1, Hence by the principle of mathematical induction, the result is true for all natural numbers n.
1 . 2 + 2 . 3 + 3 . 4 + ………. + n (n + 1) = \(\frac{\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}{3}\)
is true for all natural numbers n ≥ 1

Question 5.
Using the Mathematical induction, show that for any natural number n ≥ 2,

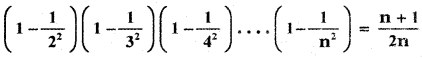
Answer:
Let

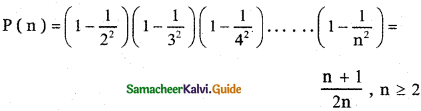
The first stage is n = 2

Step 1:
Let us verify the result for n = 2

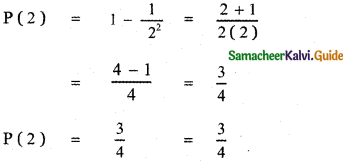
∴ The given result is true for n = 2.

Step 2:
Let us assume that the result is true for n = k.

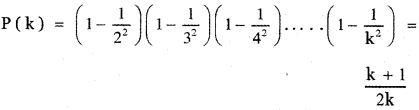
Step 3:
Let us prove the result for n = k + 1


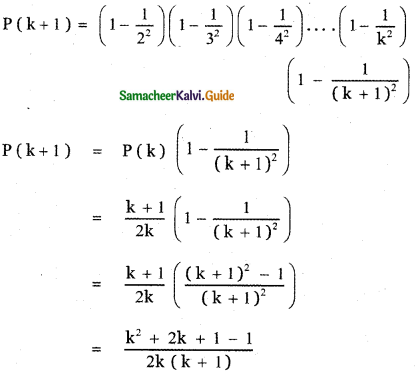
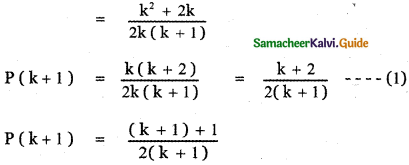
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n ≥ 2.

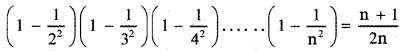
is true for all natural numbers n ≥ 2.

Question 6.
Using the Mathematical induction, show that for any natural number n ≥ 2,

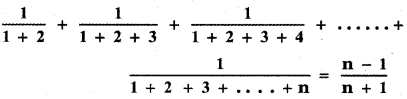
Answer:

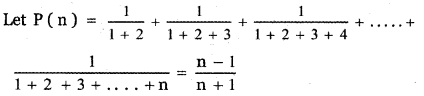
Step 1:
Since n ≥ 2 the first stage is n = 2
Let us verify the result for n = 2

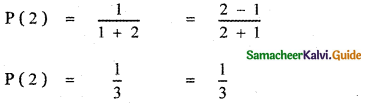
∴ P (2 ) is true.
The result is true for n = 2.

Step 2:
Let us assume that the result is true for n = k.

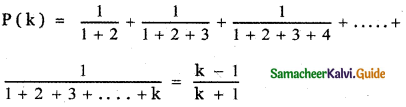
Step 3:
Let us prove the result for n = k + 1


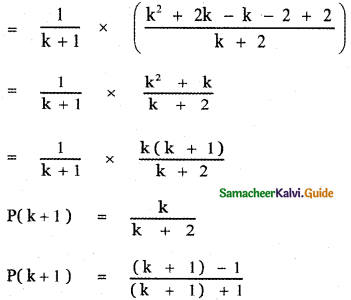
This implies p(k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n ≥ 2.

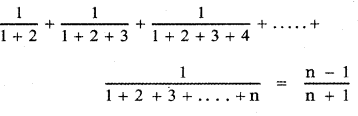
is true for all natural numbers n ≥ 2

Question 7.
Using the mathematical induction, show that for any natural number n,

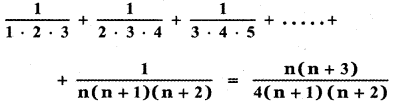
Answer:

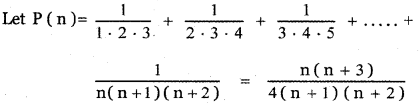
Step 1:
First, let us verify the result for n = 1

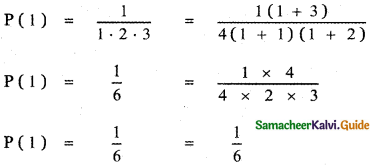
∴ The given result is true for n = 1

Step 2:
Let us assume the result for n = k

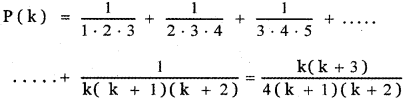
Step 3:
Let us prove the result for n = k + 1

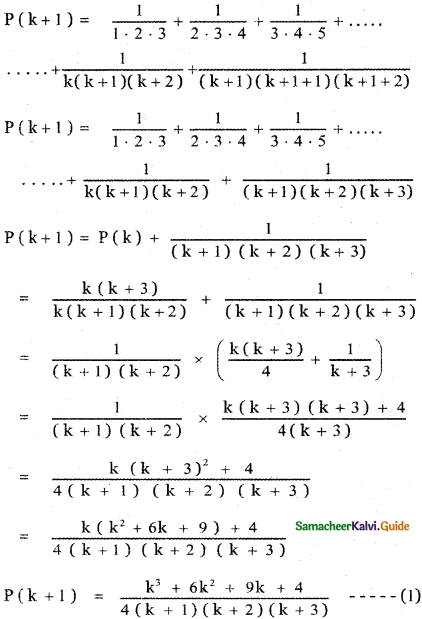
Factorizing k³ + 6k² + 9k + 4
f (k) = k³ + 6k² + 9k + 4
f(- 1) = (- 1)³ + 6(- 1)² + 9(- 1) + 4
f(- 1) = – 1 + 6 – 9 + 4 = 0
∴ (k + 1) is a factor of f(k)

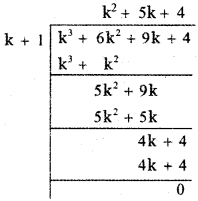
k³ + 6k² + 9k + 4 = (k + 1) (k² + 5k + 4).
= (k + 1) (k² + 4k + k + 4)
= (k + 1) [k(k + 4) + 1(k + 4)]
= (k + 1) (k + 4) (k + 1)

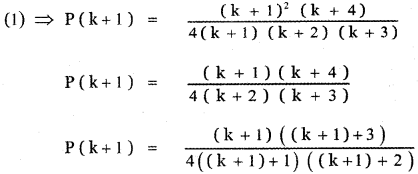
This implies P(k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

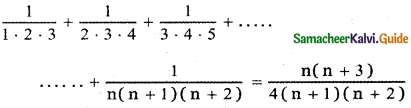
is true for all natural numbers n

Question 8.
Using the Mathematical induction, show that for any natural number n,

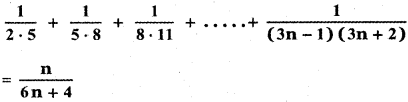
Answer:

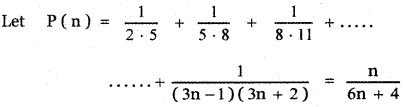
Step 1:
First, let us verify the result for n = 1


∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k

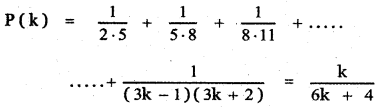
Step 3:
Let us prove the result for n = k + 1


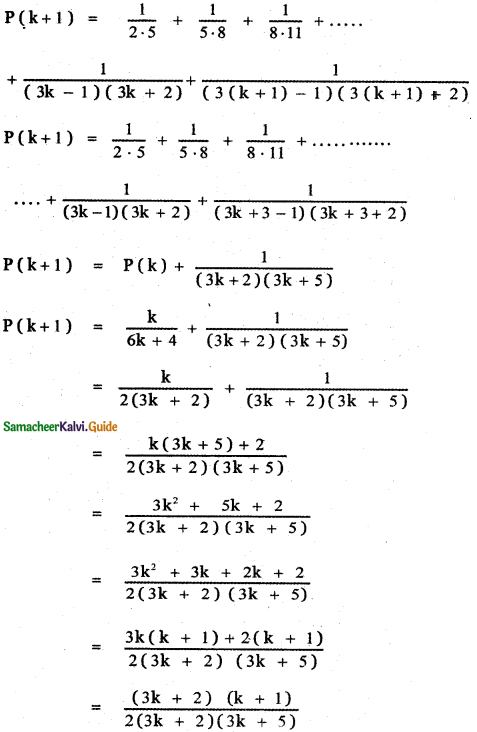
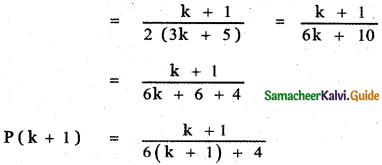
This implies P(k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

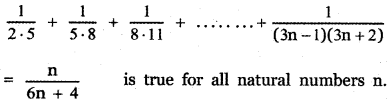
Question 9.
Prove by mathematical induction that
1! + (2 × 2 !) + (3 × 3!) +…. .+ (n × n!) = (n + 1)! – 1
Answer:
P(n) is the statement
1! + (2 × 2!) + (3 × 3!) + ….. + (n × n!) = (n + 1)! – 1
To prove for n = 1
LHS = 1! = 1
RHS = (1 + 1)! – 1 = 2! – 1 = 2 – 1 = 1
LHS = RHS ⇒ P(1) is true
Assume that the given statement is true for n = k
(i.e.) 1! + (2 × 2!) + (3 × 3!) + … + (k × k!) = (k + 1)! – 1 is true
To prove P(k + 1) is true
p(k + 1) = p(k) + t_{(k + 1)}
P(k + 1) = (k + 1)! – 1 + (k + 1) × (k + 1)!
= (k + 1)! + (k + 1) (k + 1)! – 1
= (k + 1)! [1 + k + 1] – 1
= (k + 1)! (k + 2) – 1
= (k + 2)! – 1
= (k + 1 + 1)! – 1
∴ P(k + 1) is true
⇒ P(k) is true, So by the principle of mathematical induction P(n) is true.

Question 10.
Using the Mathematical induction, show that for any natural number n, x²ⁿ – y²ⁿ is divisible by x + y.
Answer:
Let P(n) = x²ⁿ – y²ⁿ is divisible by (x + y)
For n = 1
P(1) = x^{2 × 1} – y^{2 × 1} is divisible by (x + y)
⇒ (x + y) (x – y) is divisible by (x + y)
∴ P(1) is true
Let P(n) be true for n = k
∴ P(k) = x^2k – y^2k is divisible by (x + y)
⇒ x^2k – y^2k = λ(x + y) …… (i)
For n = k + 1
⇒ P(k + 1) = x^{2(k + 1)} – y^{2(k + 1)} is divisible by (x + y)
Now x^{2(k + 2)} – y^{2(k + 2)}
= x^{2k + 2} – x^2ky² + x^2ky² – y^{2k + 2}
= x^2k.x² – x^2ky² + x^2ky² – y^2ky²
= x^2k (x² – y²) + y²λ (x + y) [Using (i)]
⇒ x^{2k + 2} – y^{2k + 2} is divisible by (x + y)
∴ P(k + 1) is true.
Thus P(k) is true ⇒ P(k + 1) is true.
Hence by the principle of mathematical induction, P(n) is true for all n ∈ N

Question 11.
By the principle of mathematical induction, prove that, for n ≥ 1, 1² + 2² + 3² + ………….. + n² > \(\frac{n^{3}}{3}\)
Answer:
Let P (n) = 1² + 2² + 3² + ………….. + n² > \(\frac{n^{3}}{3}\)

Step 1:
Let us first verify the result for n = 1

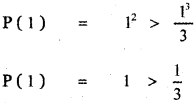
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k.
P(k) = 1² + 2² + 3² + …………… + k² > \(\frac{\mathrm{k}^{3}}{3}\)

Step 3:
Let us prove the result for n = k + 1
P(k + 1) = 1² + 2² + 3² + …………… + k² + (k + 1)²
P(k + 1) = P(k) + ( k + 1)²

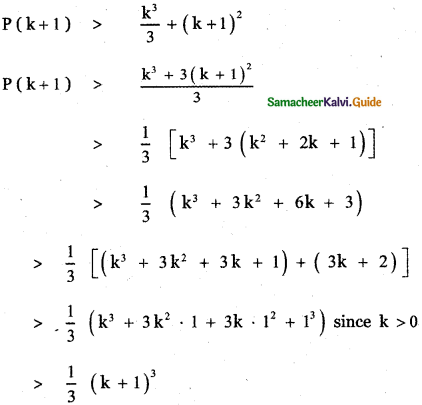
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
1² + 2² + 3² + ………….. + n² > \(\frac{n^{3}}{3}\)

Question 12.
Use induction to prove that n³ – 7n + 3, is divisible by 3, for all natural numbers n.
Answer:
Let P(n) : n³ – 7n + 3
Step 1:
P(1) = (1)³ – 7(1) + 3
= 1 – 7 + 3 = -3 which is divisible by 3
So, it is true for P(1).

Step 2:
P(k) : k³ – 7k + 3 = 3λ. Let it be true
⇒ k³ = 3λ + 7k – 3

Step 3:
P(k + 1) = (k + 1)³ – 7(k + 1) + 3
= k³ + 1 + 3k² + 3k – 7k – 7 + 3
= k³ + 3k² – 4k – 3
= (3λ + 7k – 3) + 3k² – 4k – 3 (from Step 2)
= 3k² + 3k + 3λ – 6
= 3(k² + k + λ – 2) which is divisible by 3.
So it is true for P(k + 1).
Hence, P(k + 1) is true whenever it is true for P(k).

Question 13.
Use induction to prove that 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9 , for all natural numbers n.
Answer:
To prove 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9
That is to prove 5^{n + 1} + 4 × 6ⁿ – 9 is divisible by 20
Let P (n) be the statement 5^{n + 1} + 4 × 6ⁿ
which is divisible by 20
P (n) = 5^{n + 1} + 4 × 6ⁿ – 9 = 20λ

Step 1 :
Let us verify the statement for n = 1
P (1) = 5^{i + 1} + 4 × 6¹ – 9
= 5² + 4 × 6 – 9
= 25 + 24 – 9
= 49 – 9 = 40
which is divisible by 20
∴ The statement is true for n = 1

Step 2:
Let us assume that the statement is true for n = k
P(k) = 5^{k + 1} + 4 × 6^k – 9 is divisible by 20
P(k) = 5^{k + 1} + 4 × 6^k – 9 = 20λ …………… (1)

Step 3:
Let us prove the result for n = k + 1

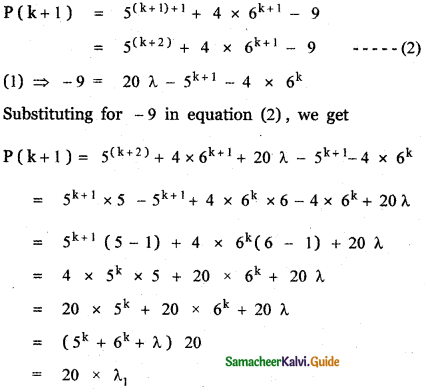
Hence, P(k + 1) is divisible by 20.
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
Thus, 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9, for all natural numbers n.

Question 14.
Use induction to prove that 10ⁿ + 3 × 4^{n + 2} + 5 is divisible by 9, for all natural numbers n.
Answer:
Let P( n) = 10ⁿ + 3 × 4^{n + 2} + 5 is divisible by 9

Step 1:
Let us verify the result for n = 1
P ( 1 ) = 10¹ + 3 × 4^{1 + 2} + 5
= 15 + 3 × 4³
= 15 + 3 × 64
= 15 + 192 = 207
which is divisible by 9
Thus we have verified the result for n = 1

Step 2:
Let us assume the result is true for n = k
P(k) = 10^k + 3 × 4^{k + 2} + 5 is divisible by 9
∴ 10^k + 3 × 4^{k + 2} + 5 = 9m for some m
10^k = 9m – 5 – 3 × 4^{k + 2} for some m

Step 3:
Let us prove the result for n = k + 1

which is divisible by 9
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
10ⁿ + 3 × 4^{n + 2} + 5 is divisible by 9,
for all natural numbers n.

Question 15.
Prove that using mathematical induction

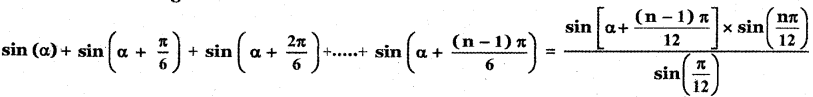
Answer:

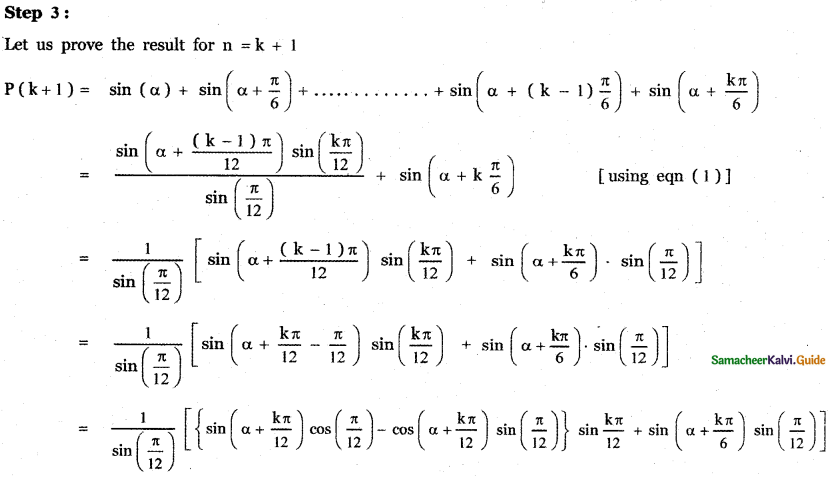
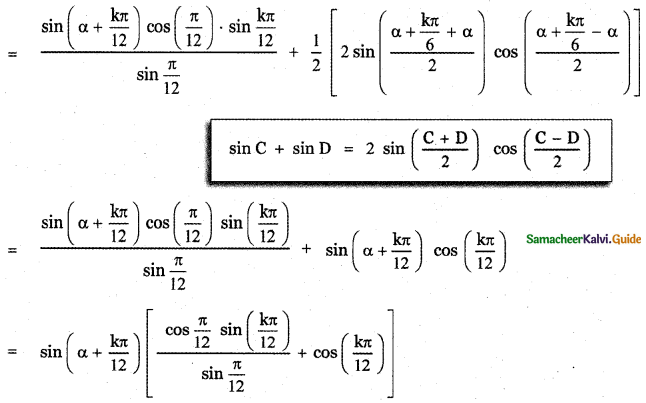
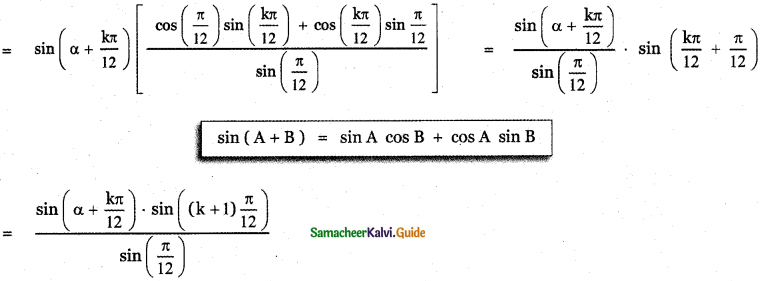
This implies P (k + 1) is true. Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.