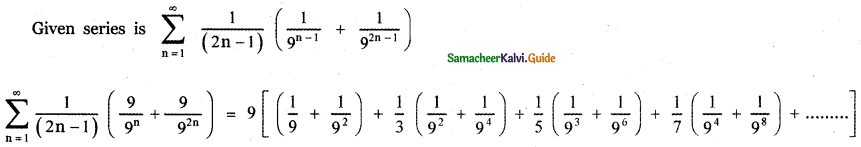Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.4
Question 1.
Expand the following in ascending powers of x and find the condition on x for which the binomial expansion is valid.
(i) \(\frac{1}{5+x}\)
Answer:
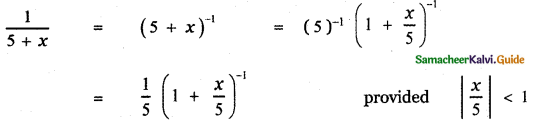

![]()
(ii) \(\frac{2}{(3+4 x)^{2}}\)
Answer:

(iii) (5 + x2)2/3
Answer:

![]()
(iv) \((x+2)^{-\frac{2}{3}}\)
Answer:
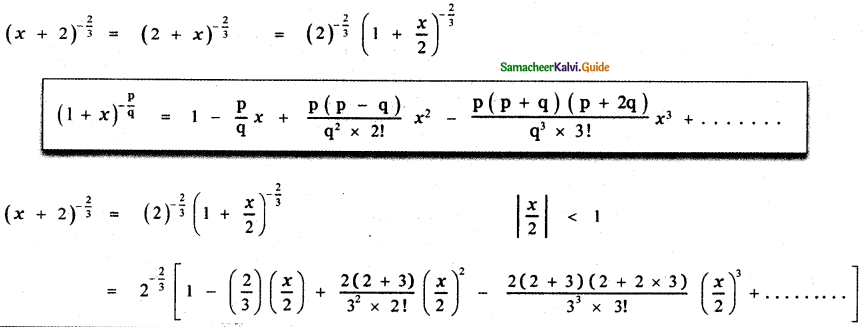
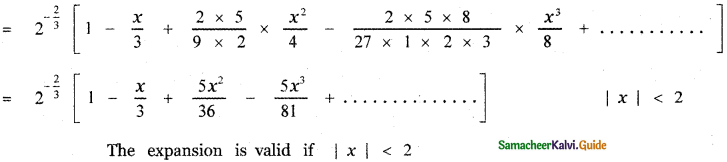
Question 2.
Find \(\sqrt[3]{1001}\) approximately. (two decimal places)
Answer:

![]()
Question 3.
Prove that \(\sqrt[3]{x^{3}+6}-\sqrt[3]{x^{3}+3}\) is approximately equal to \(\frac{1}{x^{2}}\) when x is sufficiently large.
Answer:
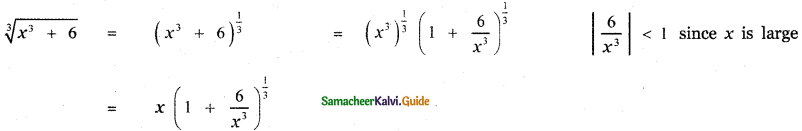


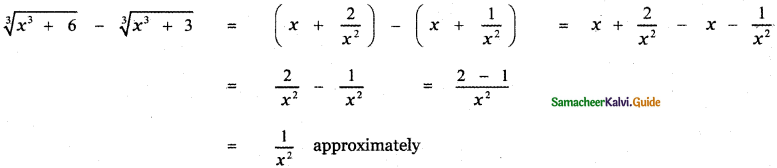
![]()
Question 4.
Prove that \(\sqrt{\frac{1-x}{1+x}}\) is approximately equal to 1 – x + \(\frac{x^{2}}{2}\) when x is very small.
Answer:

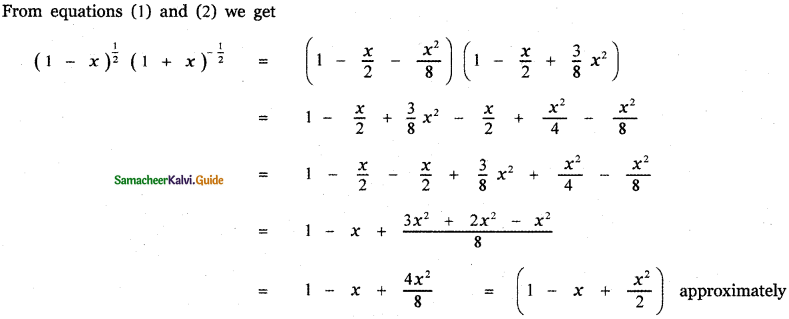
![]()
Question 5.
Write the first 6 terms of the exponential series
(i) e5x
Answer:
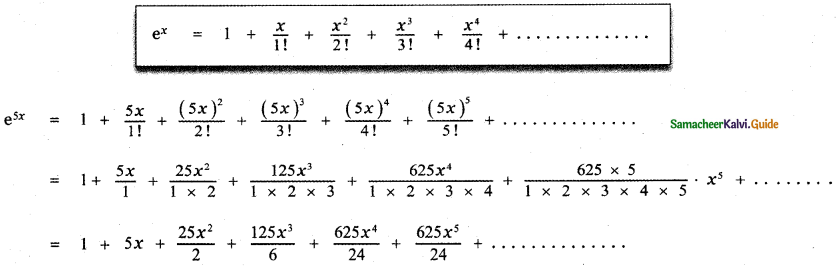
(ii) e-2x
Answer:

![]()
(iii) ex/2
Answer:
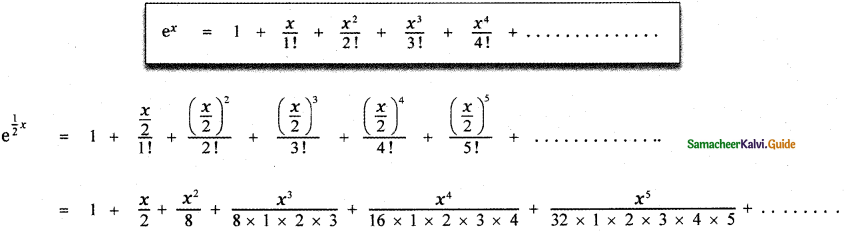
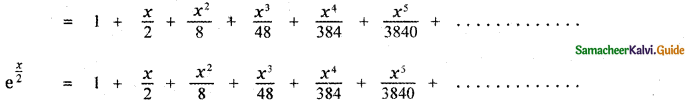
Question 6.
Write the first 4 terms of the logarithmic series.
(i) log (1 + 4x)
(ii) log (1 – 2x)
(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)
(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)
Find the intervals on which the expansions are valid.
Answer:
(i) log ( 1 + 4x )
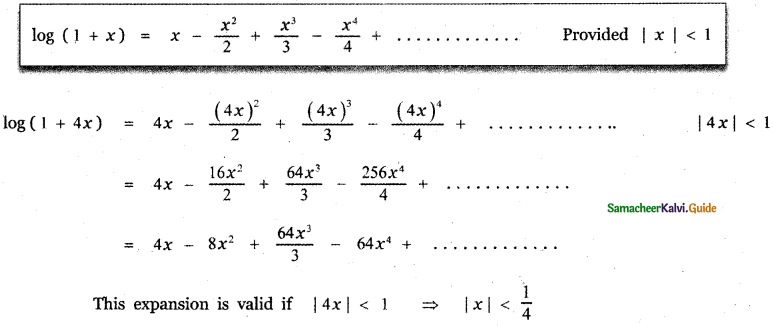
![]()
(ii) log (1 – 2x)

(iii) log \(\left(\frac{1+3 x}{1-3 x}\right)\)

![]()
(iv) log \(\left(\frac{1-2 x}{1+2 x}\right)\)

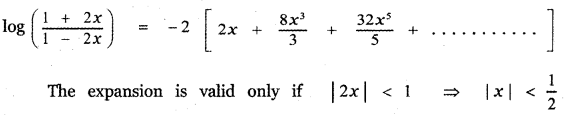
Question 7.
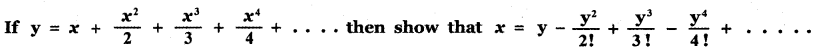
Answer:
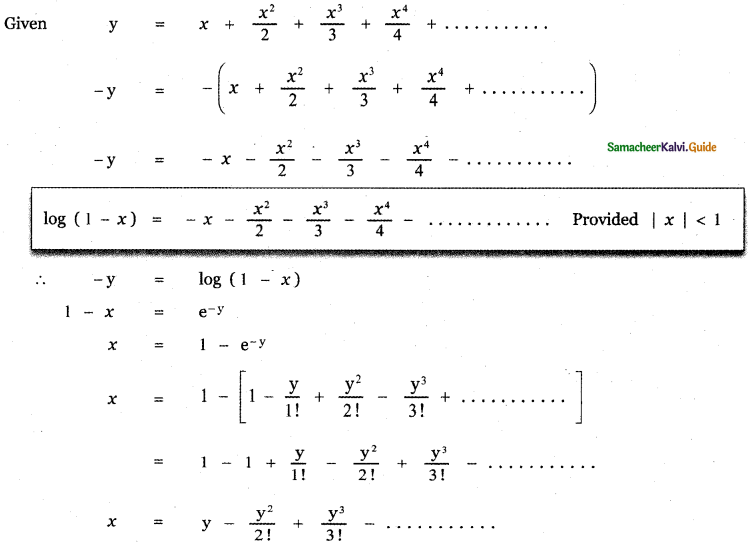
![]()
Question 8.
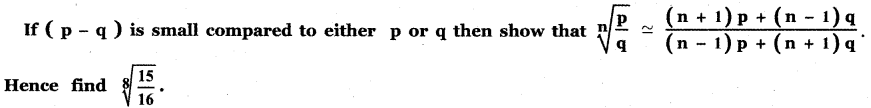
Answer:
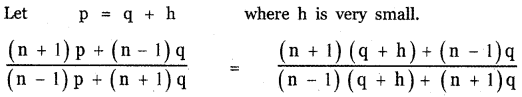


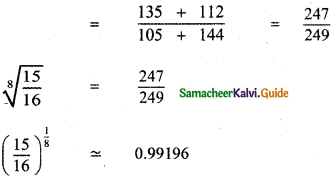
![]()
Question 9.
Find the coefficient of x4 in the expansion of \(\frac{3-4 x+x^{2}}{e^{2 x}}\)
Answer:
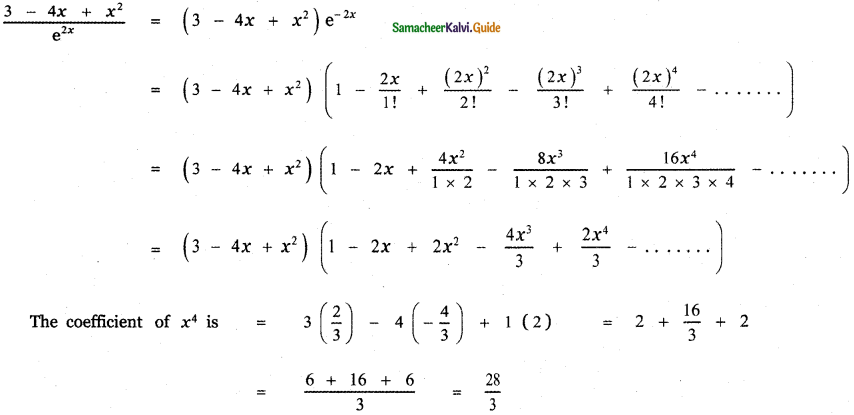
![]()
Question 10.
Find the value of 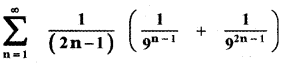
Answer: