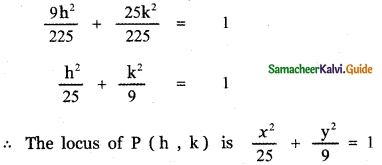Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.1
Question 1.
Find the locus of P, if for all values of a , the coordinates of a moving point P is
(i) (9 cos α, 9 sin α)
(ii) (9 cos α, 6 sin α)
Answer:
(i) (9 cos α, 9 sin α)
Let P (h , k) be any point on the required path. Then by the given data we have h = 9 cos α, k = 9 sin α
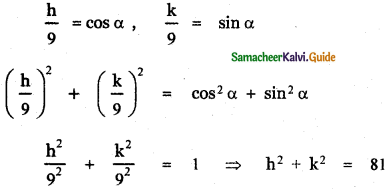
The locus of P (h , k) is obtained by replacing h by x and k by y.
∴ The required locus becomes x2 + y2 = 81
![]()
(ii) ( 9 cos α, 6 sin α)
Let P (h, k) be any point on the required path. Then by the given data we have h = 9 cos α, k = 6 sin α
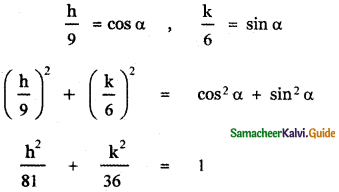
The locus of p(h , k) is obtained by replacing h by x and k by y
∴ The required locus is \(\frac{x^{2}}{81}+\frac{y^{2}}{36}\) = 1
Question 2.
Find the locus of a point P that moves a constant distant of
(i) two units from the x-axis
(ii) three units from the y-axis.
Answer:
(i) Two units from x-axis:
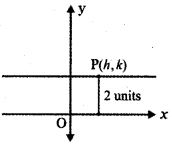
Let P (h, k) be any point on the required path. From the given data, we have k = 2
The locus of P (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is y = 2
(ii) Three units from y-axis:
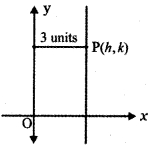
Let (h, k) be any point on the required path. From the given data, we have h = 3.
The locus of P (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is x = 3
![]()
Question 3.
If 6 is a parameter, find the equation of the locus of a moving point, whose coordinates are x = a cos3θ, y = a sin3θ.
Answer:
The given moving points is (a cos3θ, a sin3θ)
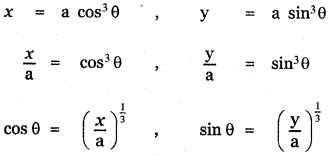

Question 4.
Find the values of k and b. If the points P(-3, 1) and Q (2, b) lie on the locus of x2 – 5x + ky = 0
Answer:
Given P (-3, 1) lie on x2 – 5x + ky = 0
⇒ (-3)2 – 5(-3) + k(1) = 0
9 + 15 + k = 0 ⇒ k = -24
Q (2, b) lie on x2 – 5x + ky = 0
(2)2 – 5(2) + k(b) = 0 ⇒ 4 – 5(2) – 24b = 0
![]()
![]()
Question 5.
A straight rod of length 8 units slides with its ends A and B always on the x and y axes respectively, then find the locus of the midpoint of the line segment AB.
Answer:
Given A and B are the ends of the straight rod of length 8 unit on the x and y-axes. Let A be (a, 0) and B (0, b).
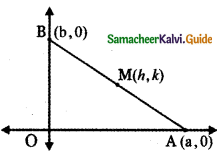
Let M (h, k) be the midpoint of AB (h,k) =
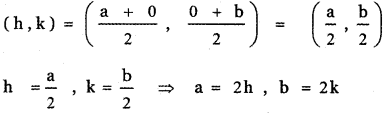
In the right-angled ∆ OAB
AB2 = OA2 + OB2
82 = a2 + b2
64 = (2h)2 + (2k)
64 = 4h2 + 4k2
h2 + k2 = \(\frac{64}{4}\) = 16
The locus of M (h, k) is obtained by replacing h by x and k by y
∴ The required locus is x2 + y2 = 16
Question 6.
Find the equation of the locus of a point such that the sum of the squares of the distance from the points (3, 5), (1, -1) is equal to 20.
Answer:
Let P (h, k) be the moving point
Let the given point be A (3, 5) and B (1, -1)
We are given PA2 + PB2 = 20
⇒ (h – 3)2 + (k – 5)2 + (h – 1)2 + (k + 1)2 = 20
⇒ h2 – 6h + 9 + k2 – 10k + 25 + h2 – 2h + 1 + k2 + 2k + 1 = 20
(i.e.) 2h2 + 2k2 – 8h – 8k + 36 – 20 = 0
2h2 + 2k2 – 8h – 8k + 16 = 0
(÷ by 2 ) h2 + k2 – 4h – 4k + 8 = 0
So the locus of P is x2 + y2 – 4x – 4y + 8 = 0
![]()
Question 7.
Find the equation of the locus of the point P such that the line segment AB, joining the points A(1 ,-6) and B(4 , – 2) subtends a right angle at P.
Answer:
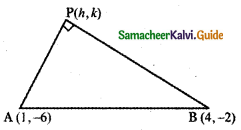
Given A (1, – 6) and B (4, – 2).
Let P (h, k) be a point such that the line segment AB subtends a right angle at P.
∴ ∆ APB is a right-angled triangle.
AB2 = AP2 + BP2 ………… (1)
AB2 = (4 – 1)2 + (- 2 + 6)2
AB2 = 32 + 42 = 9 + 16 = 25
AP2 = (h – 1)2 + (k + 6)2
BP2 = (h – 4)2 + (k + 2)2
(1) ⇒
25 = (h – 1)2 + (k + 6)2 + (h – 4)2 + (k + 2)2
25 = h2 – 2h + 1 + k2 + 12k + 36 + h2 – 8h + 16 + k2 + 4k + 4
25 = 2h2 + 2k2 – 10h + 16k + 57
2h2 + 2k2 – 10h + 16k + 57 – 25 = 0
2h2 + 2k2 – 10h + 16k + 32 = 0
h2 + k2 – 5h + 8k + 16 =0
The locus of P (h , k) is obtained by replacing h by x and k by y.
∴ The required locus is x2 + y2 – 5x + 8y + 16 = 0
Question 8.
If O is origin and R is a variable point on y2 = 4x, then find the equation of the locus of the mid-point of segment OR.
Answer:
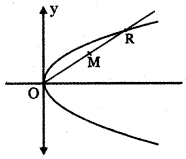
Let the variable point R be (x, y). Let M (h, k) be the midpoint of R.
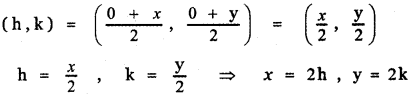
But R(x , y) is a point on y2 = 4x
∴ (2k)2 = 4(2h)
4k2 = 8h
k2 = 2h
The locus of M (h , k) is obtained by replacing h by x and k by y.
∴ The required locus is y2 = 2x
![]()
Question 9.
The coordinates of a moving point P are (\(\frac{\mathbf{a}}{2}\) (cosec θ + sin θ), \(\frac{\mathbf{b}}{2}\) (cosec θ – sin θ) where θ is a variable parameter. Show that the equation of the locus P is b2 x2 – a2 y2 = a2 b2
Answer:
Let the moving point P be (h, k)
By the given data we have
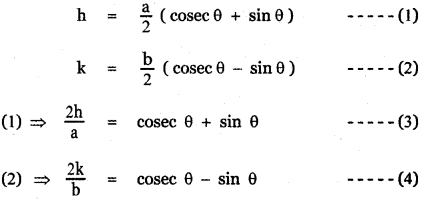

The locus of P ( h , k ) is obtained by replacing h by x and k by y
∴ The required locus is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
b2 x2 – a2 y2 = a2 b2
Question 10.
If P (2, – 7) is given point and Q is a point on 2x2 + 9y2 = 18 then find the equations of the locus of the midpoint of PQ.
Answer:
Given P is (2, -7) and let Q be (x, y)
Given that Q is a point on 2x2 + 9y2 = 18
Let M (h, k) be the midpoint of PQ
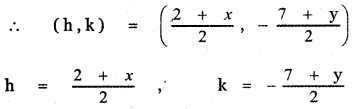
2h = 2 + x , 2k = – 7 + y
x = 2h – 2, y = 2k + 7
But Q(x, y) is a point on 2x2 + 9y2 = 18
∴ 2 (2h – 2)2 + 9 (2k + 7)2 = 18
2 [4h2 – 8h + 4] + 9 [4k2 + 28k + 49] = 18
8h2 – 16h + 8 + 36k2 + 252k + 441 = 18
8h2 + 36k2 – 16h + 252k + 449 = 18
8h2 + 36k2 – 16h + 252k +431 =0
The locus of M ( h , k ) is obtained by replacing h by x and k by y.
∴ The required locus is
8x2 + 36y2 – 16x + 252y + 431 = 0
![]()
Question 11.
If R is any point on the x-axis and Q is any point on the y-axis and P is a variable point on RQ with RP = b, PQ = a, then find the equation of locus of P.
Answer:
Given R is any point on the x-axis and Q is any point on the y-axis.
Let R be (x, 0) and Q be (0, y)
Let P (h, k ) be the variable point on RQ such that RP = b and PQ = a

The point P ( h, k ) divides the line joining the points R(x, 0) and Q (0, y) in the ratio b : a
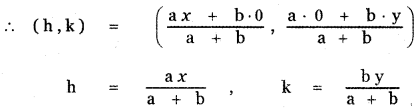
![]()
Substituting in equation (1), we have
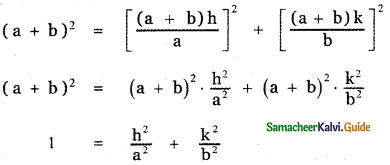
The locus of P (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is \(\frac{x^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}\) = 1
Question 12.
If the points P (6, 2) and Q (- 2, 1 ) and R are the vertices of a ∆PQR and R is the point on the locus y = x2 – 3x + 4 then find the equation of the locus of the centroid of ∆PQR.
Answer:
Given P (6, 2), Q (-2 , 1), R (a, b) are the vertices of ∆ PQR where R (a, b) lies on y = x2 – 3x + 4
∴ b = a2 – 3a + 4 (1)
Let the centroid of ∆ PQR be G (h, k)
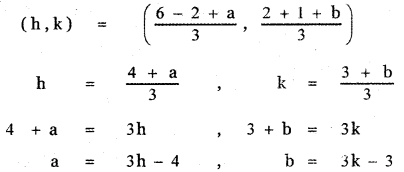
Substituting in equation (1) we have
(1) ⇒ 3k – 3 = (3h – 4)2 – 3(3h – 4) + 4
3k – 3 = 9h2 – 24h + 16 – 9h + 12 + 4
9h2 – 33h + 32 – 3k + 3 = 0
9h2 – 33h – 3k + 35 = 0
The locus of G (h, k) is obtained by replacing h by x and k by y.
∴ The required locus is 9x2 – 33x – 3y + 35 = 0
![]()
Question 13.
If Q is a point on the locus of x2 + y2 + 4x – 3y +7 = 0, then find the equation of locus of P which divides segment OQ externally in the ratio 3 :4 where O is origin.
Answer:
Let Q be (a, b) lying on the locus
x2 + y2 + 4x – 3y + 7 = 0
∴ a2 + b2 + 4a – 3b + 7 = 0
Let the movable point P be (h , k)
Given P divides OQ externally in the ratio 3 : 4
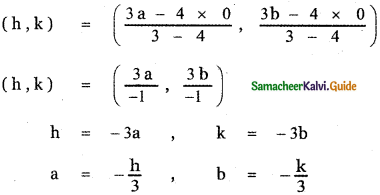
Substituting in equation (1) we have
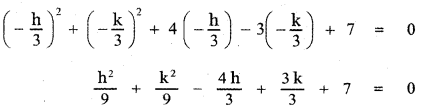
h2 + k2 – 12h + 9k + 63 = 0
The locus of P(h, k) is obtained by replacing h by x and k by y.
∴ The required locus is
x2 + y2 – 12x + 9y + 63 = 0
Question 14.
Find the points on the locus of points that are 3 units from the x-axis and 5 units from the point (5, 1)
Answer:
Given that the required pointis3unitsfrom x-axis and 5 units from the point P (5, 1). Let Q (h, 3) and K (h,- 3) be the required points.
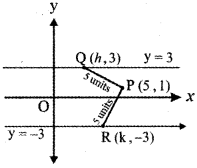
∴ PQ = 5
\(\sqrt{(5-\mathrm{h})^{2}+(1-3)^{2}}\) = 5
(5 – h)2 + (- 2)2 = 25
25 – 10h + h2 + 4 = 25
h2 – 10h + 29 – 25 = 0
h2 – 10h + 4 = 0

PR = 5
![]()
(5 – k)2 + 42 = 25
25 – 10k + k2 + 16 = 25
k2 – 10k + 16 = 0
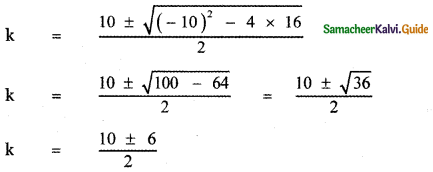

∴ R (8, – 3), (2, – 3)
∴ Required points are
(5 + √21, 3), (5 – √21, 3), (8, – 3), (2, – 3)
![]()
Question 15.
The sum of the distance of a moving point from the points (4, 0) and (- 4, 0) is always 10 units. Find the equation to the locus of the moving point.
Answer:
Let A be (4, 0) and B be (-4, 0). Let the moving point be p(h, k)
Given PA + PB = 10

16h2 + 200h + 625 = 25[h2 + 8h + 16 + k2]
16h2 + 200h + 625 = 25h2 + 200h + 400 + 25k2
9h2 + 26k2 = 225