Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.1
![]()
Question 1.
Construct an m × n matrix A = [aij], where aij is given by
(i) aij = \(\frac{(\mathbf{i}-2 \mathbf{j})^{2}}{2}\) with m = 2 , n = 3
(ii) aij = \(\frac{|3 \mathbf{i}-4 \mathbf{j}|}{4}\) with m = 3 , n = 4
Answer:
(i) aij = \(\frac{(\mathbf{i}-2 \mathbf{j})^{2}}{2}\) with m = 2 , n = 3
To construct 2 × 3 matrices.
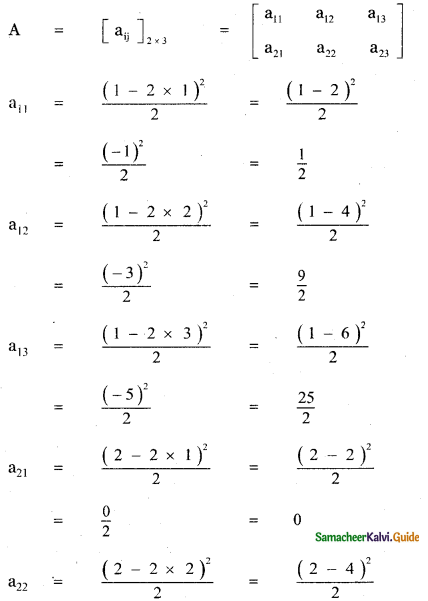
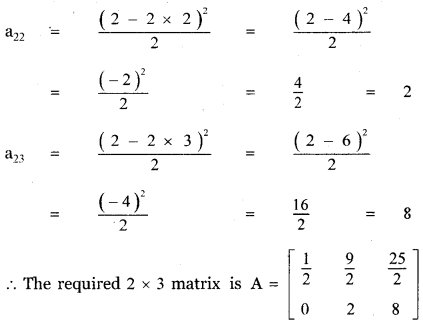
![]()
(ii) aij = \(\frac{|3 \mathbf{i}-4 \mathbf{j}|}{4}\) with m = 3 , n = 4
To construct a 3 × 4 matrices.



![]()

Question 2.
Find the value of p, q, r and s if
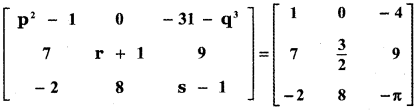
Answer:
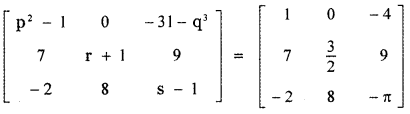
Equating the corresponding entries
⇒ p2 – 1 = 1
⇒ p2 = 1 + 1 = 2
p = ± \(\sqrt{2}\)
-31 – q3 = -4
-q3 = -4 + 31 = 27
q3 = -27 = (-3)3
⇒ q = -3
r + 1 = \(\frac{3}{2}\)
⇒ r = \(\frac{3}{2}\) – 1 = \(\frac{3-2}{2}\) = \(\frac{1}{2}\)
s – 1 = π
⇒ s = – π + 1 (i.e.,) s = 1 – π
So, p = ± \(\sqrt{2}\), q = -3, r = 1/2 and s = 1 – π
![]()
Question 3.
Determine the value of x + y if
\(\left[ \begin{matrix} 2x\quad +\quad y & 4x \\ 5x\quad -\quad 7 & 4x \end{matrix} \right] \) = \(\left[ \begin{matrix} 7 & 7y\quad -\quad 13 \\ y & x\quad +\quad 6 \end{matrix} \right]\)
Answer:
\(\left[\begin{array}{cc}{2 x+y} & {4 x} \\ {5 x-7} & {4 x}\end{array}\right]=\left[\begin{array}{cc}{7} & {7 y-13} \\ {y} & {x+6}\end{array}\right]\)
⇒ 2x + y = 7 ………….. (1)
4x = 7y – 13 ………….. (2)
5x – 7 = y …………… (3)
4x = x + 6 ……………. (4)
from (4) 4x – x = 6
3x = 6 ⇒ x = \(\frac{6}{3}\) = 2
Substituting x = 2 in (1), we get
2(2) + y = 7 ⇒ 4 + y = 7 ⇒ y = 7 – 4 = 3
So x = 2 and y = 3
∴ x + y = 2 + 3 = 5
![]()
Question 4.
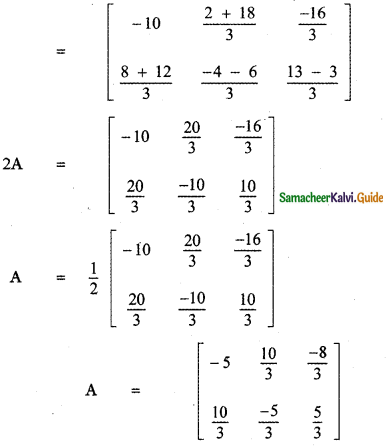
Determine the matrices A and B if they satisfy 2A – B + \(\left[ \begin{matrix} 6 & -6 & 0 \\ -4 & 2 & 1 \end{matrix} \right] \) = 0 and A – 2B = \(\left[ \begin{matrix} 3 & 2 & 8 \\ -2 & 1 & -7 \end{matrix} \right] \)
Answer:


![]()
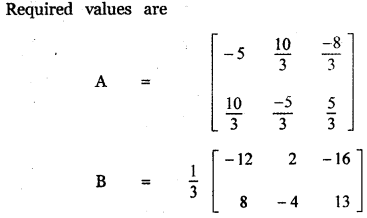
Question 5.
If A = \(\left[ \begin{matrix} 1 & a \\ 0 & 1 \end{matrix} \right] \), then compute A4
Answer:

![]()
Question 6.
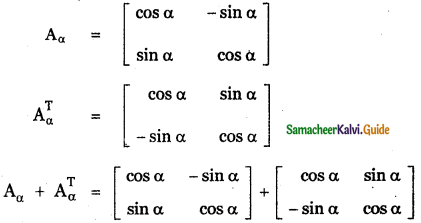
Consider the matrix Aα = \(\left[ \begin{matrix} cos\quad α & -\quad sin\quad α \\ sin\quad α & cos\quad α \end{matrix} \right] \)
(i) Show that AαAβ = A(α+β)
Answer:
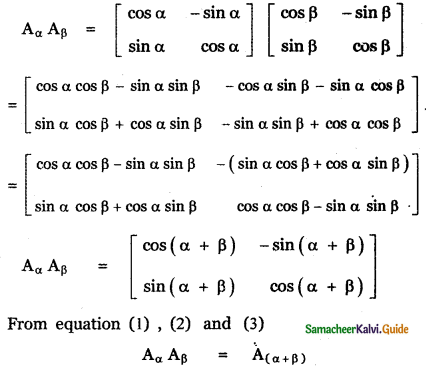
(ii) Find all possible real values α satisfying the condition Aα + AαT = I
Answer:

![]()
Question 7.
If A = \(\left[ \begin{matrix} 4 & 2 \\ -1 & x \end{matrix} \right] \) and such that (A – 2I) (A – 3I) = 0, find the value of x.
Answer:


![]()

Question 8.
If A = \(\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ a & b & -1 \end{matrix} \right] \), show that A2 is a unit matrix.
Answer:
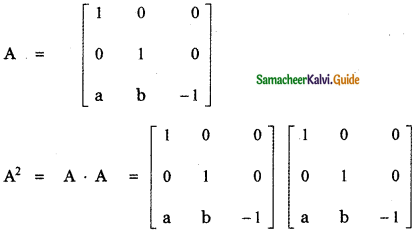
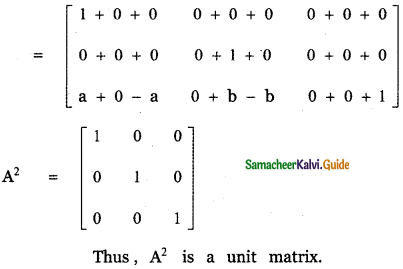
![]()
Question 9.
If A = \(\left[ \begin{matrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{matrix} \right]\) and A3 – 6A2 + 7A + kI = 0, find the value of k.
Answer:

![]()

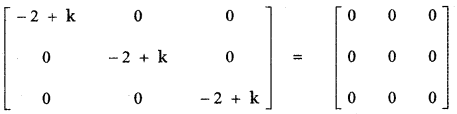
Equating the corresponding entries – 2 + k = 0 ⇒ k = 2
∴ The required value of k is k = 2
Question 10.
Give your own examples of matrices satisfying the following conditions in each case:
(i) A and B such that AB ≠ BA
(ii) A and B such that AB = 0 = BA, A ≠ 0 and B ≠ 0.
(iii) A and B such that AB = 0 and BA ≠ 0
Answer:
(i) A and B such that AB ≠ BA
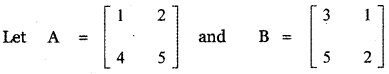
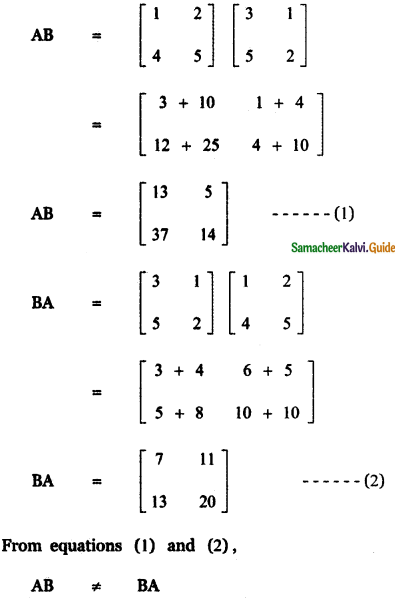
![]()
(ii) A and B such that AB = 0 = BA, A ≠ 0 and B ≠ 0.
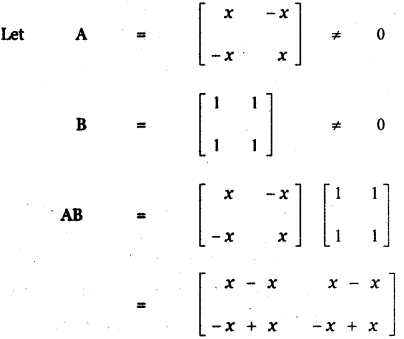

(iii) A and B such that AB = 0 and BA ≠ 0
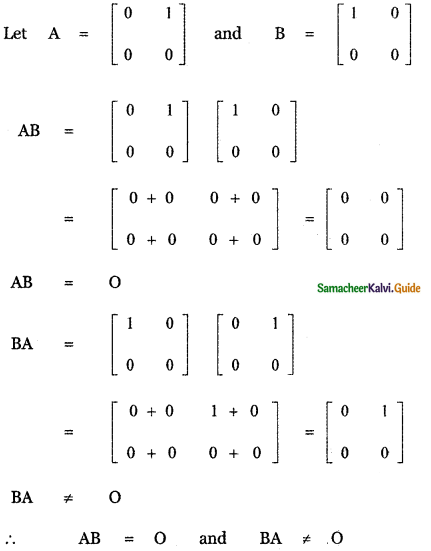
![]()
Question 11.
Show that f(x) f(y) = f(x + y) , where f(x) = \(\left[ \begin{matrix} cos\quad x & -\quad sin\quad x & 0 \\ sin\quad x & cos\quad x & 0 \\ 0 & 0 & 1 \end{matrix} \right] \)
Answer:

![]()
Question 12.
If A is a square matrix such that A2 = A, find the value of 7A – (I + A )3
Answer:
Given A2 = A
So 7A – (I + A)3 = 7A – (I + 3A + 3A2 + A3]
= 7A – I – 3A – 3 A2 – A3
Given A2 = A
7A – I – 3A – 3A – A3 = -I + A – A3
= -I + A – (A2 × A)
= -I + A – (A × A) = -I + A – A2
= -I + A – A = -I
So the value of 7A – (I + A)3 = -I.
Question 13.
Verify the property A (B + C) = AB + AC, when the matrices A, B, and C are given by
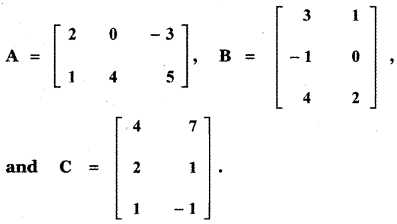
Answer:
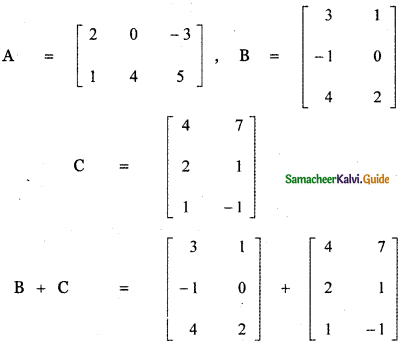
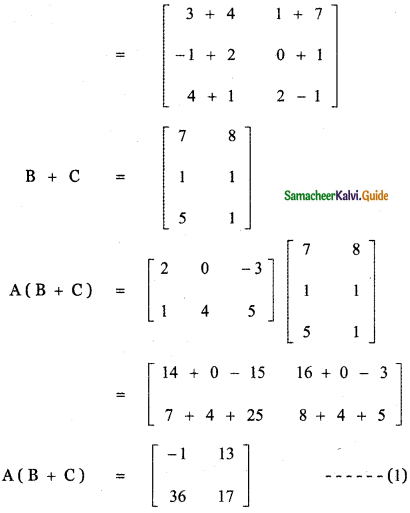
![]()
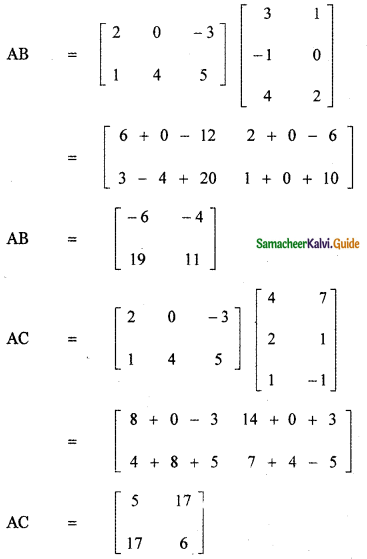

![]()
Question 14.
Find the matrix A which satisfies the matrix relation A\(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right] \) = \(\left[ \begin{matrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{matrix} \right] \)
Answer:


![]()
Question 15.
If AT = \(\left[ \begin{matrix} 4 & 5 \\ -1 & 0 \\ 2 & 3 \end{matrix} \right] \) and B = \(\left[ \begin{matrix} 2 & -1 & 1 \\ 7 & 5 & -2 \end{matrix} \right] \)
verify the following
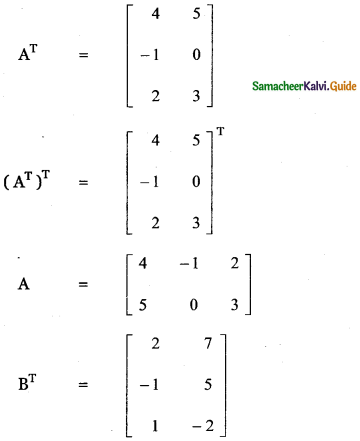
(i) (A + B)T = AT + BT = BT + AT
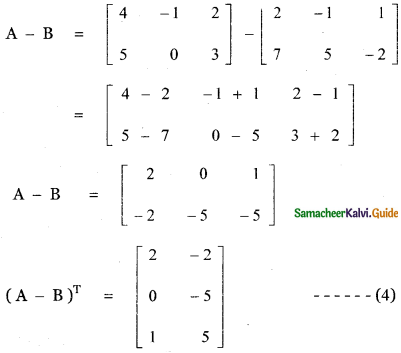
(ii) (A – B)T = AT – BT
(iii) (BT)T = B
Answer:
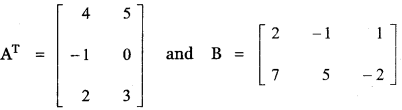
(i) (A + B)T = AT + BT = BT + AT

![]()

(ii) (A – B)T = AT – BT

![]()
(iii) (BT)T = B

Question 16.
If A is a 3 × 4 matrix and B is a matrix such that both ATB and BAT are defined, what is the order of the matrix B?
Answer:
A is a matrix of order 3 × 4
So AT will be a matrix of order 4 × 3
AT B will be defined when B is a matrix of order 3 × n
BAT will be defined when B is of order m × 4
from (1) and (2) we see that B should be a matrix of order 3 × 4
![]()
Question 17.
Express the following matrices as the sum of a symmetric matrix and a skew – symmetric matrix:
(i) \(\left[ \begin{matrix} 4 & -2 \\ 3 & -5 \end{matrix} \right] \)
Answer:



A = \(\frac{1}{2}\)(A + AT) + \(\frac{1}{2}\)(A – AT
Thus A is expressed as a sum of a symmetric and skew-symmetric matrix.
![]()
(ii) \(\left[ \begin{matrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2 \end{matrix} \right] \)
Answer:


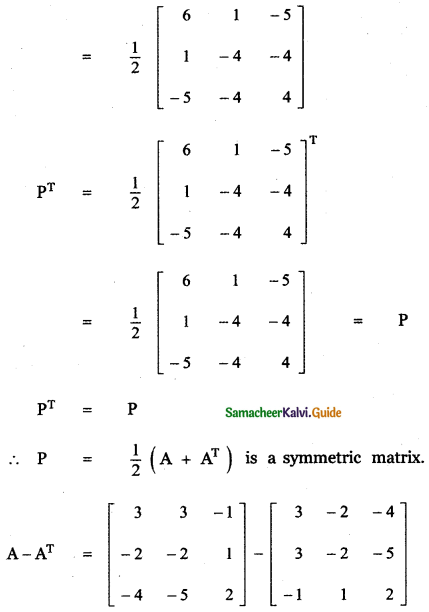
![]()


![]()
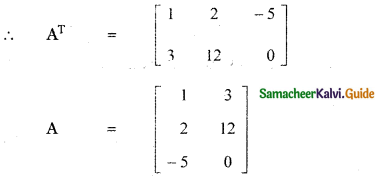
Question 18.
Find the matrix A such that
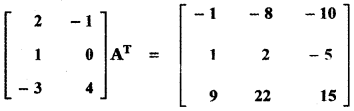
Answer:

Equating like entries
2a – d = -1, 2b – e = – 8, 2c – f = -10
a = 1, b = 2, c = -5
2a – d = -1 ⇒ 2 × 1 – d = – 1
⇒ 2 + 1 = d ⇒ d = 3
2b – e = – 8 ⇒ 2 × 2 – e = – 8
⇒ 4 + 8 = e ⇒ e = 12
2c – f = -10 ⇒ 2 × – 5 – f = -10
⇒ – 10 – f = -10 ⇒ f = 0
![]()
Question 19.
If A = \(\left[ \begin{matrix} 1 & 2 & 2 \\ 2 & 1 & -\quad 2 \\ x & 2 & y \end{matrix} \right] \) is a matrix such that AAT = 9I, find the values of x and y.
Answer:

Equating the corresponding entries
x + 4 + 2y = 0 ………… (1)
2x + 2 – 2y = o ………… (2)
x + 4 + 2y = 0 ………… (3)
2x + 2 – 2y = 0 ………… (4)
x2 + 4 + y2 = 9 ………… (5)
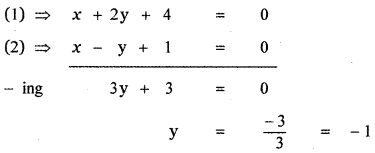
Substituting the value of y in equation (1) we have
x + 4 + 2x – 1 = 0
x + 4 – 2 = 0 ⇒ x = – 2
Substituting x = – 2 and y = – 1 in equation(5) we have
(5) ⇒ (-2)2 + 4 + (- 1)2 = 9
4 + 4 + 1 = 9
9 = 9
∴ The required values of x and y are
x = – 2 and y = – 1
![]()
Question 20.
(i) For what value of x, the matrix A = \(\left[ \begin{matrix} 0 & 1 & -\quad 2 \\ -\quad 1 & 0 & { x }^{ 3 } \\ 2 & -\quad 3 & 0 \end{matrix} \right] \) is skew – symmetric
Answer:
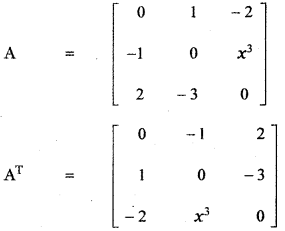
The matrix A is skew-symmetric if A = – AT

Equating the corresponding entries
x3 – 3 = 0
x3 = 3 ⇒ x = 31/3
![]()
(ii) If \(\left[ \begin{matrix} 0 & p & 3 \\ 2 & { q }^{ 2 } & -\quad 1 \\ r & 1 & 0 \end{matrix} \right] \) is skew – symmetric find the values of p, q and r.
Answer:

A is skew-symmetric if A = – AT
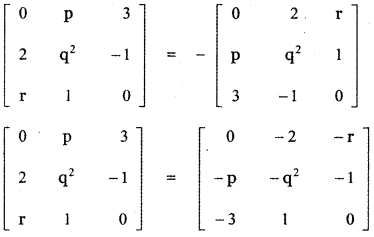
Equating the corresponding entries.
p = – 2 , r = – 3
q2 = -q2 ⇒ q2 + q2 = 0
⇒ 2q2 = 0 ⇒ q = 0
∴ The required values are
p = – 2 , q = 0 , r = – 3
![]()
Question 21.
Construct the matrix A = [aij]3×3 , where aij = 1 – j. State whether A is symmetric or skew – symmetric.
Answer:
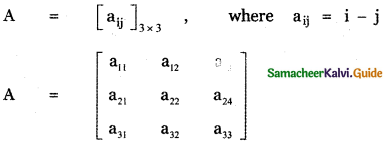
aij = i – j
a11 = 1 – 1 = 1
a12 = 1 – 2 = – 1
a13 = 1 – 3 = – 2
a21 = 2 – 1= 1
a22 = 2 – 2 = 1
a23 = 2 – 3 = – 1
a31 = 3 – 1= 2
a32 = 3 – 2 = 1
a33 = 3 – 3 = 0
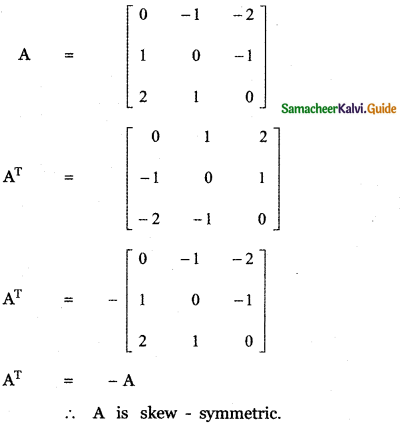
![]()
Question 22.
Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix.
Answer:
Given A and B two symmetric matrices.
∴ A = AT and B = BT
First, let us assume AB = BA.
Let us prove AB is a symmetric matrix.

∴ AB is a symmetric matrix.
conversely let us assume that AB is a symmetric matrix.
we prove AB = BA
AB is symmetric then

![]()
Question 23.
If A and B are symmetric matrices of the same order, prove that
(i) AB + BA is a symmetric matrix
(ii) AB – BA is a skew-symmetric matrix.
Answer:
Given A and B are symmetric matrices
⇒ – AT = A and BT = B
(i) To prove AB + BA is a symmetric matrix.
Proof: Now (AB + BA)T = (AB)T + (BA)T = BTAT + ATBT
= BA + AB = AB + BA
i.e. (AB + BA)T = AB + BA
⇒ (AB + BA) is a symmetric matrix.
(ii) To prove AB – BA is a skew symmetric matrix.
Proof: (AB – BA)T = (AB)T – (BA)T = BTAT – ATBT = BA – AB
i.e. (AB – BA)T = – (AB – BA)
⇒ AB – BA is a skew symmetric matrix.
![]()
Question 24.
A shopkeeper in a Nuts and Spices shop makes gift packs of cashew nuts, raisins, and almonds. The pack contains 100 gm of cashew nuts, 100 gm of raisins, and 50 gm of almonds. Pack – II contains 200 gm of cashew nuts, 100 gm of raisins, and 100 gm of almonds. Pack -III contains 250 gm of cashew nuts, 250 gm of raisins, and 150 gm of almonds. The cost of 50 gm of cashew nuts is ₹ 50, 50 gm of raisins is ₹ 10, and 50 gm of almonds is ₹ 60. What is the cost of each gift pack?
Answer:
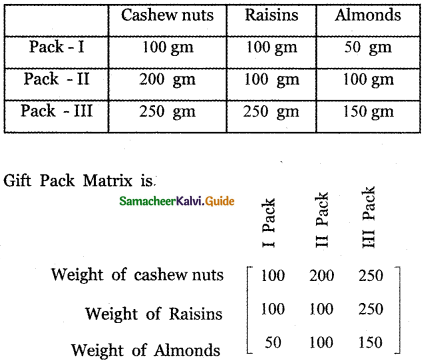
Let us consider 50 gm of cashew nuts as one unit, 50 gms of raisins as one unit 50 gm of almonds as one unit.
∴ The Gift pack matrix becomes

Also given 50 gms of Cashew nuts cost = Rs. 50
50 gms of Raisins cost = Rs. 10
50 gms of Almonds cost = Rs. 60
∴ Cost matrix is B = [50 10 60]
∴ Cost of cash gift pack = BA
![]()

∴ Cost of I gifts Pack = Rs. 180
Cost of II gift Pack = Rs.340
Cost of III gift Pack = Rs. 480