Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 Vector Algebra – I Ex 8.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.1
Question 1.
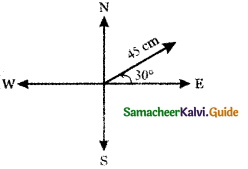
Represent graphically the displacement of
(i) 45cm, 30° north of east
(ii) 80 km, 60° south of west
Answer:
(i) 45cm, 30° north of east
(ii) 80 km, 60° south of west
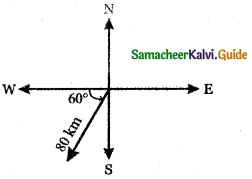
![]()
Question 2.
Prove that the relation R defined on the set V of all vectors by ‘\(\vec{a}\) R \(\vec{b}\) if \(\vec{a}\) = \(\vec{b}\)’ is an equivalence relation on V.
Answer:

![]()
Question 3.
Let \(\vec{a}\) and \(\vec{b}\) be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are \(\frac{\overrightarrow{\mathbf{a}}+2 \overrightarrow{\mathbf{b}}}{3}\) and \(\frac{\overrightarrow{\mathbf{b}}+2 \overrightarrow{\mathbf{a}}}{3}\).
Answer:

Question 4.
If D and E are the midpoints of the sides AB and AC of a triangle ABC, prove that \(\overrightarrow{\mathbf{B E}}\) and \(\overrightarrow{\mathbf{D C}}\) = \(\frac{3}{2} \overrightarrow{\mathrm{BC}}\)
Answer:
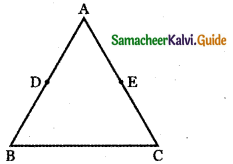


![]()
Question 5.
Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
Answer:
ABC be the triangle and D, E, F is the midpoints of the sides AB, BC, and AC respectively.
Let O be the origin and let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are the position vectors of the points A, B and C respectively.
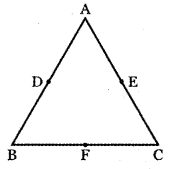

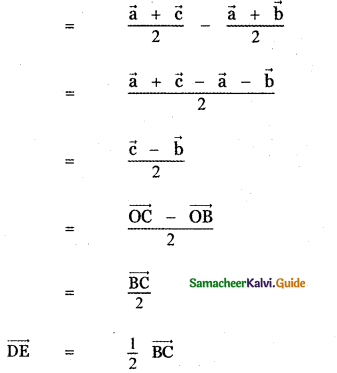
∴ \(\overrightarrow{\mathbf{D E}}\) is parallel to \(\overrightarrow{\mathbf{B C}}\) and length of DE is half the length of BC. Similarly we can prove \(\overrightarrow{\mathbf{E F}}\) = \(\frac{1}{2} \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{EF}}\)
parallel to \(\overrightarrow{\mathbf{A B}}\) and length of E is half the length of AB.
Also \(\overrightarrow{\mathbf{D F}}\) = \(\frac{1}{2} \overrightarrow{\mathrm{AC}}\)
\(\overrightarrow{\mathbf{D F}}\) is parallel to \(\overrightarrow{\mathbf{A C}}\) and length of DF is half the length of AC . Thus, the line segment joining the mid points of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
![]()
Question 6.
Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Answer:
Let ABCD be any quadrilateral D, E, F, G are the midpoints of the sides AB, BC, CD, AD respectively.
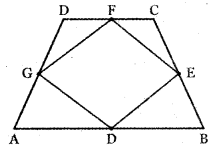




∴ EF and DG are parallel and equal.
∴ In the quadrilateral, DEFG’s opposite sides are parallel and equal. Therefore, DEFG is a parallelogram.
![]()
Question 7.
If \(\vec{a}\) and \(\vec{b}\) represent a side and a diagonal of a parallelogram , find the other sides and the other diagonal.
Answer:
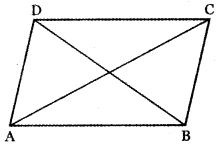
Let ABCD be a parallelogram
Let \(\overrightarrow{\mathbf{A B}}\) = \(\vec{a}\)
\(\overrightarrow{\mathbf{A C}}\) = \(\vec{b}\)
Since ABCD is a parallelogram , we have


Question 8.
If \(\overline{\mathbf{P O}}+\overline{\mathbf{O Q}}\) = \(\overline{\mathbf{Q O}}+\overline{\mathbf{O R}}\), prove that the points P , Q , R are collinear.
Answer:
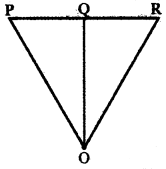
Let P, Q , R be the given points . Let O be the origin. Then the position vectors of
P, Q, R are \(\overrightarrow{\mathrm{OP}}\), \(\overrightarrow{\mathrm{OQ}}\) and \(\overrightarrow{\mathrm{OR}}\).

∴ P, Q, R lie on a straight line.
Hence, P, Q, R are collinear.
![]()
Question 9.
If D is the midpoint of the aide BC of i triangle ABC , prove that \(\overrightarrow{\mathbf{A B}}\) + \(\overrightarrow{\mathbf{A C}}\) = 2 \(\overrightarrow{\mathbf{A D}}\)
Answer:
Given D is the mid point of the side BC of a triangle ABC
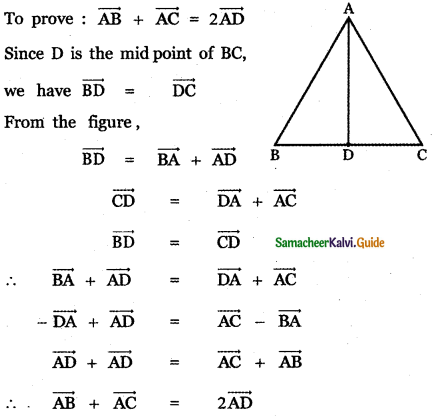
Question 10.
If G is the centroid of a triangle ABC, prove that \(\overrightarrow{\mathbf{G A}}+\overrightarrow{\mathbf{G B}}+\overrightarrow{\mathbf{G C}}=\overrightarrow{\mathbf{0}}\)
Answer:
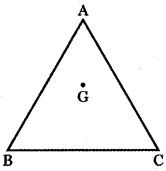
Let ABC be the triangle with centroid G. Let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) be the position vectors of the vertices A, B and C respectively with respect to the origin O. Then

![]()
Question 11.
Let A, B, and C be the vertices of a triangle. Let D, E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that \(\overrightarrow{\mathbf{A D}}+\overrightarrow{\mathbf{B E}}+\overrightarrow{\mathbf{C F}}=\overrightarrow{\mathbf{0}}\)
Answer:
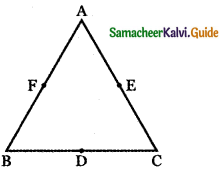
Let ABC be the triangle. D, E, F are the mid points of the sides BC , CA , AB respectively . Let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) be the position vectors of the vertices A, B, C respectively. Then

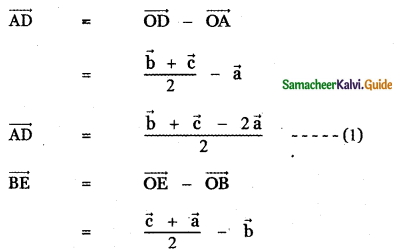

![]()
Question 12.
If ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then Prove that \(\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{A D}}+\overrightarrow{\mathbf{C B}}+\overrightarrow{\mathbf{C D}}=4 \overrightarrow{\mathbf{E F}}\)
Answer:
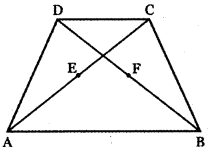
Given that ABCD is a quadrilateral. E and F are the midpoints of AC and BD.


