Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 Vector Algebra – I Ex 8.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.2
![]()
Question 1.
Verify whether the following ratios are direction cosines of some vector or not.
(i) \(\frac{1}{5}, \frac{3}{5}, \frac{4}{5}\)
(ii) \(\frac{1}{\sqrt{2}}, \frac{1}{2}, \frac{1}{2}\)
(iii) \(\frac{4}{3}, 0, \frac{3}{4}\)
Answer:
(i) \(\frac{1}{5}, \frac{3}{5}, \frac{4}{5}\)
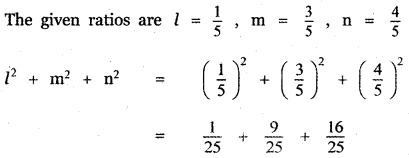
![]()
[If l, m, n are direction cosines of a vector then l2 + m2 + n2 = 1]
∴ The given ratio \(\frac{1}{5}, \quad \frac{3}{5}, \quad \frac{4}{5}\) do not form the direction cosines of a vector.
(ii) \(\frac{1}{\sqrt{2}}, \frac{1}{2}, \frac{1}{2}\)
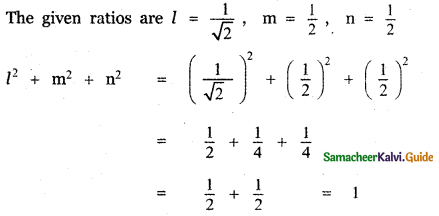
[If l, m, n are direction cosines of a vector then l2 + m2 + n2 = 1]
∴ The given ratio form the direction cosines of a vector.
(iii) \(\frac{4}{3}, 0, \frac{3}{4}\)
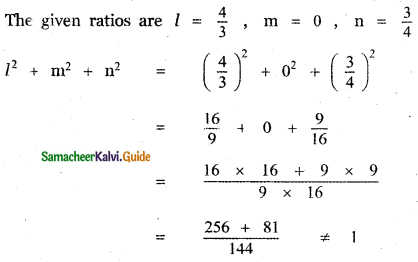
[If l, m, n are direction cosines of a vector then l2 + m2 + n2 = 1]
∴ The given ratio do not form the direction cosines of a vector.
![]()
Question 2.
Find the direction cosines of a vector whose direction ratios are
(i) 1, 2, 3
(ii) 3, -1 , 3
(iii) 0, 0, 7
Answer:
(i) 1, 2, 3
The given direction ratios are a = 1, b = 2 , c = 3

(ii) 3, – 1, 3
The given direction ratios are a = 3, b = – 1 , c = 3

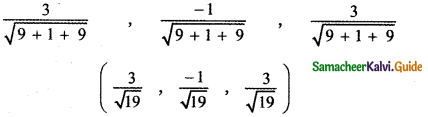
(iii) 0, 0, 7
The given direction ratios are a = 0, b = 0, c = 7

![]()
Question 3.
Find the direction cosines and direction ratios for the following vectors.
(i) 3î – 4ĵ + 8k̂
Answer:


(ii) 3î + ĵ + k̂
Answer:

(iii) ĵ
Answer:
ĵ = 0î + ĵ + 0k̂
The direction ratios of the vector ĵ are (0, 1, 0)
The direction cosines of the vector ĵ are
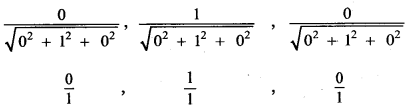
(0, 1, 0)
Direction ratios = (0, 1, 0)
Direction cosines = (0, 1, 0)
(iv) 5î – 3ĵ – 48k̂
Answer:

(v) 3î – 3k̂ + 4ĵ
Answer:

(vi) î – k̂
Answer:
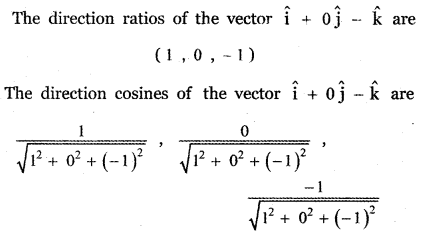

![]()
Question 4.
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians.
Answer:
Let ABC be the triangle and D, E, F is the midpoints of the sides BC, CA, AB respectively. Then AD, BE, CF are the medians of ∆ ABC.
Given that the vertices of the triangle are A (1, 0, 0) , B (0, 1, 0 ) and C (0, 0, 1).





![]()
Question 5.
If \(\frac{1}{2}, \frac{1}{\sqrt{2}}\), a are the direction cosines of some vector, then find a.
Answer:
Given \(\frac{1}{2}, \frac{1}{\sqrt{2}}\), a are the direction cosines of some vector, then
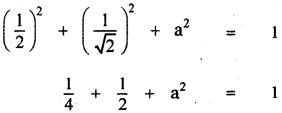

[If l, m, n are direction cosines of a vector then l2 + m2 + n2 = 1]
Question 6.
If (a, a + b , a + b + c)is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c.
Answer:
Let A be the point (1, 0, 0) and B be the point (0, 1, 0) (i.e.,) \(\overrightarrow{\mathrm{OA}}=\hat{i}\) and \(\overrightarrow{\mathrm{OB}}=\hat{j}\)
Then \(\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}=\hat{j}-\hat{i}=-\hat{i}+\hat{j}\)
= (-1, 1, 0)
= (a, a + b, a + b + c)
⇒ a = -1, a + b = 1 and a + b + c = 0
Now a = -1 ⇒ -1 + b = 1 ;a + b + c = 0
⇒ b = 2; -1 + 2 + c = 0 ⇒ c + 1 = 0
⇒ c = -1
∴ a = -1; b = 2; c = -1.
Note: If we taken \(\overrightarrow{\mathrm{BA}}\) then we get a = 1, b = -2 and c = 1.
![]()
Question 7.
Show that the vectors 2î – ĵ + k̂ , 3î – 4ĵ – 4k̂, î – 3ĵ – 5k̂ form a right angled triangle.
Answer:

Question 8.
Find the value of λ for which the vector \(\vec{a}\) = 3î + 2ĵ + 9k̂ and \(\vec{b}\) = î + λĵ + 3k̂ are parallel.
Answer:

![]()
Question 9.
Show that the following vectors are coplanar
(i) î – 2ĵ + 3k̂, – 2î + 3ĵ – 4k̂, – ĵ + 2k̂
Answer:


(ii) 5î + 6ĵ + 7k̂, 7î – 8ĵ + 9k̂, 3î + 20ĵ + 5k̂
Answer:
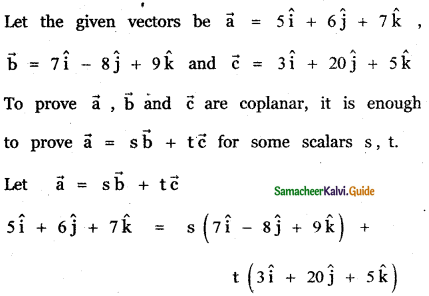

![]()
Question 10.
Show that the points whose position vectors 4î + 5ĵ + k̂, – ĵ – k̂, 3î + 9ĵ + 4k̂ and -4î + 4ĵ + 4k̂ are coplanar.
Answer:
Let the given position vectors of the points A, B, C, D be


Equating the like terms on both sides
-4 = 3s – 7t ………… (1)
-6 = 10s – 5t ……….. (2)
-2 = 5s …………. (3)
(3) ⇒ s = \(-\frac{2}{5}\)
Substituting in equation (2) , we have
-6 = 10 × \(-\frac{2}{5}\) – 5t
-6 = -4 – 5t
-6 + 4 = -5t
⇒ -5t = -2
⇒ t = \(\frac{2}{5}\)
Substituting for s and t in equation (1), we have

![]()
Question 11.
If \(\vec{a}\) = 2î + 3ĵ – 4k̂ , \(\vec{b}\) = 3î – 4ĵ – 5k̂ and \(\vec{c}\) = – 3î + 2ĵ + 3k̂ , find the magnitude and direction cosines of
(i) \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)
(ii) 3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\)
Answer:
The given vectors are \(\vec{a}\) = 2î + 3ĵ – 4k̂ , \(\vec{b}\) = 3î – 4ĵ – 5k̂ \(\vec{c}\) = – 3î + 2ĵ + 3k̂
(i) \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)

(ii) 3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\)


![]()
Question 12.
The position vectors of the vertices of a triangle are î + 2ĵ + 3k̂ ; 3î – 4ĵ + 5k̂ and – 2î + 3ĵ – 7k̂. Find the perimeter of the triangle.
Answer:
Let A, B, C be the vertices of a triangle ABC.
Given the position vectors of the vertices A, B, C are given by


∴ The required perimeter of the triangle ABC is given by AB + BC + AC = \(\sqrt{44}+\sqrt{218}+\sqrt{110}\)
![]()
Question 13.
Find the unit vector parallel to
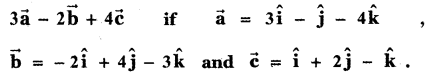
Answer:
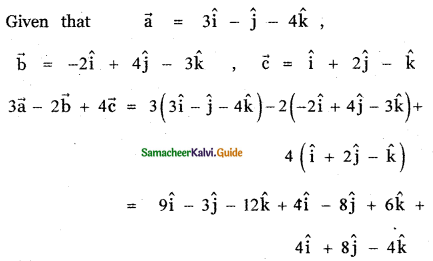

Question 14.
The position vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) of three points satisfy the relation 2 \(\vec{a}\) + 7\(\vec{b}\) + 5\(\vec{c}\) = \(\vec{0}\). Are these points collinear?
Answer:


![]()
Question 15.
The position vector of the points P, Q, R, S are î + ĵ + k̂, 2î + 5ĵ, 3î + 2ĵ – 3k̂ and î – 6ĵ – k̂ respectively. Prove that the line and PQ and RS are parallel.
Answer:
Given that the position vector of the given points P, Q, R, S are


Question 16.
Find the value or values of m for which m (î + ĵ + k̂) is a unit vector.
Answer:
The given vector is m (î + ĵ + k̂)
Given that it is a unit vector.
∴ |m (i + j + k)| = 1
|m (i + j + k)| = 1
m (± \(\sqrt{1^{2}+1^{2}+1^{2}}\)) = 1
m = ± \(\frac{1}{\sqrt{3}}\)
![]()
Question 17.
Show that points A (1, 1, 1), B (1, 2, 3), and C (2, -1, 1 ) are vertices of an isosceles triangle.
Answer:
The given vertices of a triangle are
A(1, 1, 1) ,B(1 , 2, 3) and C (2, – 1, 1)
Position vector of A is \(\overrightarrow{\mathrm{OA}}\) = î + ĵ + k̂
Position vector of B is \(\overrightarrow{\mathrm{OB}}\) = î + 2ĵ + 3k̂
Position vector of C is \(\overrightarrow{\mathrm{OC}}\) = 2î – ĵ + k̂


∴ A, B, C are not collinear.
Hence A, B, C form a triangle.
AB = CA = √5
∴ ∆ABC is an isosceles triangle.