Samacheer Kalvi 11th Maths Guide Chapter 8 Vector Algebra – I Ex 8.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 Vector Algebra – I Ex 8.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.5

Choose the correct or the most suitable answer from the given four alternatives:

Question 1.
The value of \(\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{B C}}+\overrightarrow{\mathbf{D A}}+\overrightarrow{\mathbf{C D}}\) is
(1) \(\overrightarrow{\mathbf{A D}}\)
(2) \(\overrightarrow{\mathbf{C A}}\)
(3) \(\overrightarrow{0}\)
(4) \(-\overrightarrow{\mathbf{A D}}\)
Answer:
(3) \(\overrightarrow{0}\)

Explaination:

Question 2.
If \(\overrightarrow{\mathbf{a}}+2 \overrightarrow{\mathbf{b}}\) and \(3 \overrightarrow{\mathbf{a}}+\mathbf{m} \overrightarrow{\mathbf{b}}\) are parallel, then the value of m is
(1) 3
(2) \(\frac{1}{3}\)
(3) 6
(4) \(\frac{1}{6}\)
Answer:
(3) 6

Explaination:

Question 3.
The unit vector parallel to the resultant of the vectors î + ĵ – k̂ and î – 2ĵ + k̂ is
(1)
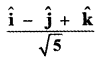
(2)
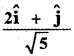
(3)
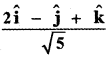
(4)
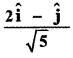
Answer:
(4)

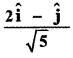
Explaination:

Question 4.
A vector \(\overrightarrow{\mathbf{O P}}\) makes 60° and 45° with the positive direction of the x and y axes respectively. Then the angle between \(\overrightarrow{\mathbf{O P}}\) and the z – axis is
(1) 45°
(2) 60°
(3) 90°
(4) 30°
Answer:
(2) 60°

Explaination:
Given the angle made by \(\overrightarrow{\mathbf{O P}}\) with x – axis and y – axis are 60° and 45° respectively. Let the angle made by \(\overrightarrow{\mathbf{O P}}\) with the positive direction of z – axis be θ. Then

Question 5.
If \(\overrightarrow{\mathbf{B A}}\) = 3î + 2ĵ + k̂ and the position vector of B is î + 3ĵ – k̂ then the position vector A is
(1) 4î + 2ĵ + k̂
(2) 4î + 5ĵ
(3) 4î
(4) – 4î
Answer:
(2) 4î + 5ĵ

Explaination:

Question 6.
A vector makes equal angle with the positive direction of the coordinate axes . Then each angle is equal to
(1) cos^-1\(\left(\frac{1}{3}\right)\)
(2) cos^-1\(\left(\frac{2}{3}\right)\)
(3) cos^-1\(\left(\frac{1}{\sqrt{3}}\right)\)
(4) cos^-1\(\left(\frac{2}{\sqrt{3}}\right)\)
Answer:
(3) cos^-1\(\left(\frac{1}{\sqrt{3}}\right)\)

Explaination:
Let the angles made by a vector with the coordinate axes be α, α, α. Then
cos² α + cos² α + cos² α = 1
[If α, β, γ are the angles made by a vector with coordinate axes respectively, then
cos² α + cos² β + cos² γ = 1]
3 cos² α = 1

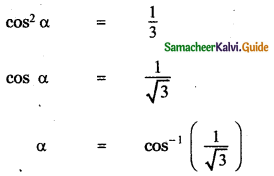
Question 7.
The vector \(\overrightarrow{\mathbf{a}}-\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{b}}-\overrightarrow{\mathbf{c}}, \overrightarrow{\mathbf{c}}-\overrightarrow{\mathbf{a}}\) are
(1) parallel to each other
(2) unit vectors
(3) mutually perpendicular vectors
(4) coplanar vectors
Answer:
(4) coplanar vectors

Explaination:

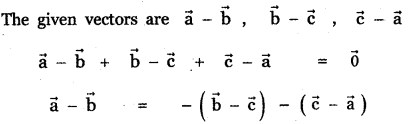
[The condition for the three vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) to be coplanar is \(\vec{a}\) = λ\(\vec{a}\) + μ\(\vec{b}\) where λ, μ are scalars. That is one vector is a Linear combination of the other two vectors.]

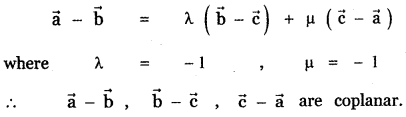
Question 8.
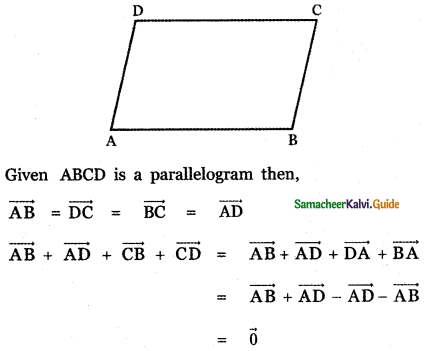
If ABCD is a parallelogram, then \(\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{A D}}+\overrightarrow{\mathbf{C B}}+\overrightarrow{\mathbf{C D}}\) is equal to
(1) 2 \((\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{A D}})\)
(2) 4 \(\overrightarrow{\mathbf{A C}}\)
(3) 4 \(\overrightarrow{\mathbf{B D}}\)
(4) \(\overrightarrow{0}\)
Answer:
(4) \(\overrightarrow{0}\)

Explaination:

Question 9.
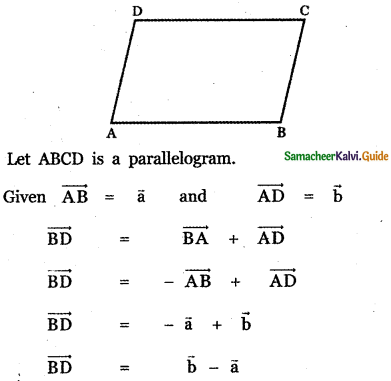
One of the diagonals of parallelogram ABCD with \(\vec{a}\) and \(\vec{b}\) as adjacent sides is \(\vec{a}\) + \(\vec{b}\). The other diagonal BD is
(1) \(\vec{a}\) – \(\vec{b}\)
(2) \(\vec{b}\) – \(\vec{a}\)
(3) \(\vec{a}\) + \(\vec{b}\)
(4) \(\frac{\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}}{2}\)
Answer:
(2) \(\vec{b}\) – \(\vec{a}\)

Explaination:

Question 10.
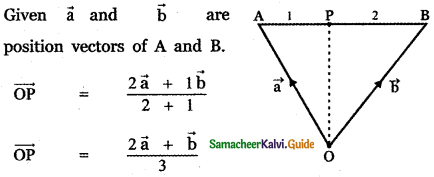
If \(\vec{a}\), \(\vec{b}\) are the vectors A and B, then which one o the following points whose position vector lies on AB, is
(1) \(\vec{a}\) + \(\vec{b}\)
(2) \(\frac{2 \vec{a}-\vec{b}}{2}\)
(3) \(\frac{2 \vec{a}+\vec{b}}{3}\)
(4) \(\frac{\vec{a}-\vec{b}}{3}\)
Answer:
(3) \(\frac{2 \vec{a}+\vec{b}}{3}\)

Explaination:

Question 11.
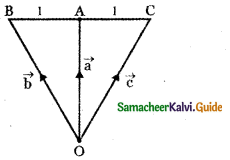
If \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) are the position vectors of three collinear points, then which of the following is true?
(1) \(\overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}\)
(2) \(2 \overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}\)
(3) \(\overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}}\)
(4) \(4 \overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}=0\)
Answer:
(2) \(2 \overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}\)

Explaination:

Question 12.
If \(\vec{r}\) = \(\frac{9 \vec{a}+7 \vec{b}}{16}\), then the point p whose position vector \(\vec{r}\) divides the line joining the points with position vectors \(\vec{a}\) and \(\vec{b}\) in the ratio
(1) 7 : 9 internally
(2) 9 : 7 internally
(3) 9 : 7 externally
(4) 7 : 9 externally
Answer:
(1) 7 : 9 internally

Explaination:

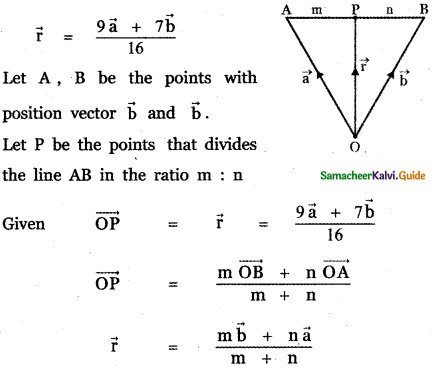
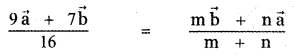
Question 13.
If λî + 2λĵ + 2λk̂ is a unit vector, then the value of λ is
(1) \(\frac{1}{3}\)
(2) \(\frac{1}{4}\)
(3) \(\frac{1}{9}\)
(4) \(\frac{1}{2}\)
Answer:
(1) \(\frac{1}{3}\)

Explaination:

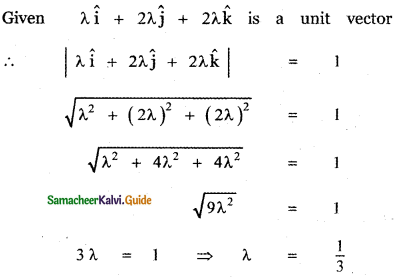
Question 14.
Two vertices of a triangle have position vectors 3î + 4ĵ – 4k̂ and 2î + 3ĵ + 4k̂. If the position vector of the centroid is î + 2ĵ + 3k̂, then the position vector of the third vertex is
(1) – 2î – ĵ + 9k̂
(2) – 2î – ĵ – 6k̂
(3) 2î – ĵ + 6k̂
(4) – 2î + ĵ + 6k̂
Answer:
(1) – 2î – ĵ + 9k̂

Explaination:
Let ABC be a triangle with centroid G. Given that

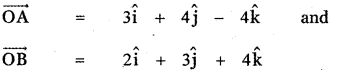
Question 15.

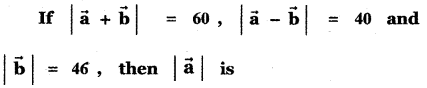
(1) 42
(2) 12
(3) 22
(4) 32
Answer:
(3) 22

Explaination:

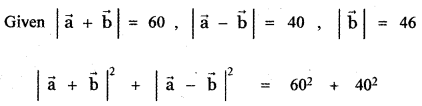
Question 16.
If \(\vec{a}\) and \(\vec{b}\) having same magnitude and angle between them is 60° and their scalar product \(\frac{1}{2}\) is then |\(\vec{a}\)| is
(1) 2
(2) 3
(3) 7
(4) 1
Answer:
(4) 1

Explaination:

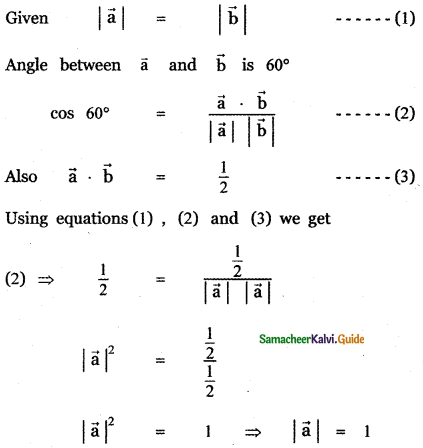
Question 17.
The value of θ ∈ (0, \(\frac{\pi}{2}\)) for which the vectors \(\vec{a}\) = (sin θ) î + (cos θ) ĵ and \(\vec{b}\) = î – √3ĵ + 2k̂ are perpendicular is equal to
(1) \(\frac{\pi}{3}\)
(2) \(\frac{\pi}{6}\)
(3) \(\frac{\pi}{4}\)
(4) \(\frac{\pi}{2}\)
Answer:
(1) \(\frac{\pi}{3}\)

Explaination:

Question 18.

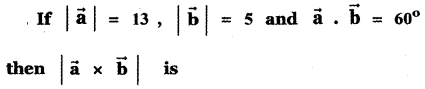
(1) 15
(2) 35
(3) 45
(4) 25
Answer:
(4) 25

Explaination:

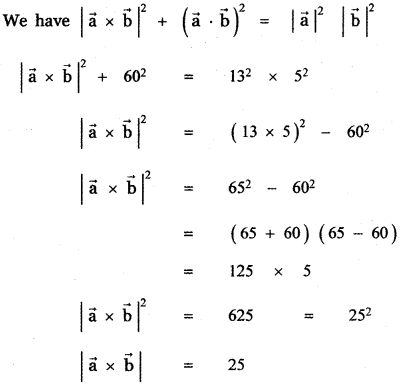
Question 19.

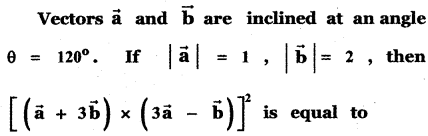
(1) 225
(2) 275
(3) 325
(4) 300
Answer:
(4) 300

Explaination:

Question 20.
If \(\vec{a}\) and \(\vec{b}\) are two vectors of magnitude 2 and inclined at an angle 60°, then the angle between \(\vec{a}\) and \(\vec{a}\) + \(\vec{b}\) is
(1) 30°
(2) 60°
(3) 45°
(4) 90°
Answer:
(1) 30°

Explaination:

Question 21.
If the projection of 5î – ĵ – 3k̂ on the vector î + 3ĵ + λk̂ is same as the projection of î + 3ĵ + λk̂ on 5î – ĵ – 3k̂, then λ is equal to
(1) ± 4
(2) ± 3
(3) ± 5
(4) ± 1
Answer:
(3) ± 5

Explaination:

Question 22.
If (1, 2, 4) and (2, – 3λ – 3) are the initial and terminal points of the vector î + 5ĵ – 7k̂ then the value of λ is equal to
(1) \(\frac{7}{3}\)
(2) \(-\frac{7}{3}\)
(3) \(-\frac{5}{3}\)
(4) \(\frac{7}{3}\)
Answer:
(4) \(\frac{7}{3}\)

Explaination:


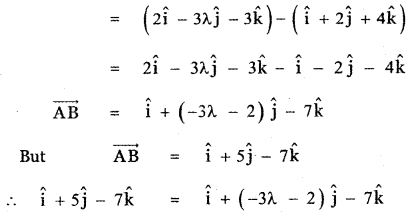
Equating the like terms
5 = – 3λ – 2
3λ = – 5 – 2 = – 7
λ = \(-\frac{7}{3}\)

Question 23.
If the points whose position vectors 10î + 3ĵ, 12î – 5ĵ and aî + 11ĵ are collinear then a is equal to
(1) 6
(2) 3
(3) 5
(4) 8
Answer:
(4) 8

Explaination:
The position vectors of the three points are

The condition for the three points A, B, C are collinear is the area of the triangle formed by these points is zero.

Question 24.

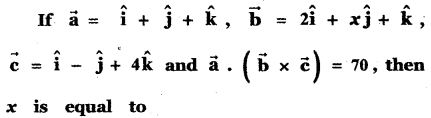
(1) 5
(2) 7
(3) 26
(4) 10
Answer:
(3) 26

Explaination:


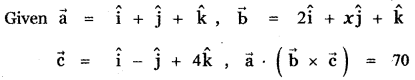
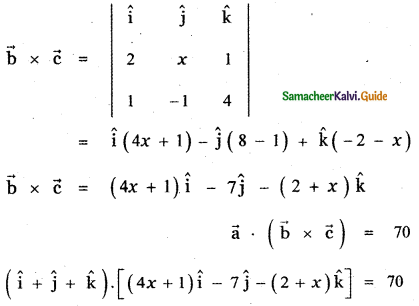
(4x + 1) – 7 – (2 + x) = 70
4x + 1 – 7 – 2 – x = 70
3x – 8 = 70
3x = 70 + 8
3x = 78
x = \(\frac{78}{3}\) = 26

Question 25.
If \(\vec{a}\) = î + 2ĵ + 2k̂, |\(\vec{b}\)| = 5 and the angle between \(\vec{a}\) and \(\vec{b}\) is \(\frac{\pi}{6}\), then the area of the triangle formed by these two vectors as two sides, is
(1) \(\frac{7}{4}\)
(2) \(\frac{15}{4}\)
(3) \(\frac{3}{4}\)
(4) \(\frac{17}{4}\)
Answer:
(2) \(\frac{15}{4}\)

Explaination: