Samacheer Kalvi 11th Maths Guide Chapter 9 Limits and Continuity Ex 9.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 9 Limits and Continuity Ex 9.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.1

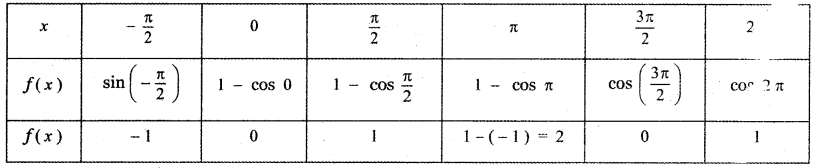
In Problems 1 – 6, complete the table using calculator and use the result to estimate the limit.

Question 1.


Answer:

Question 2.


Answer:

Question 3.


Answer:

Question 4.


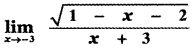
Answer:

Question 5.


Answer:

Question 6.


Answer:

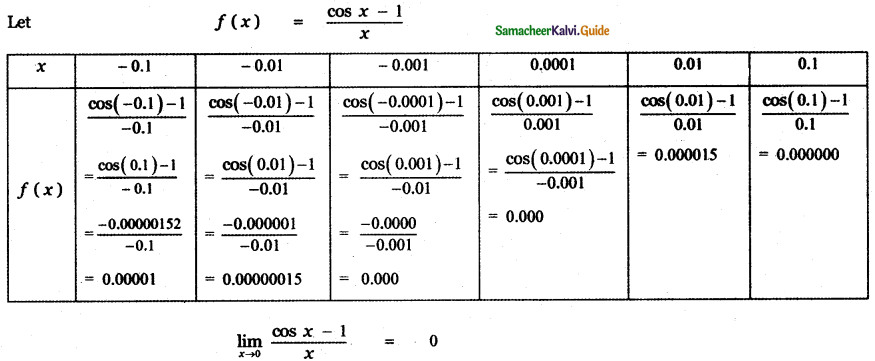
Question 7.

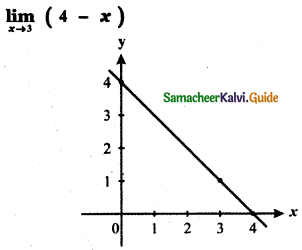
Answer:

From the graph the value of the function at x = 3 is y = f(3) = 1

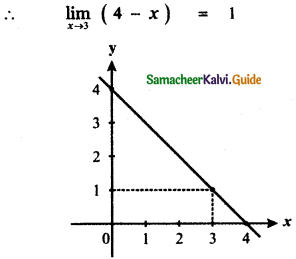
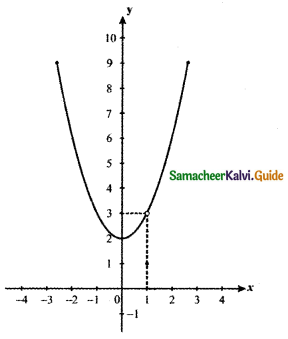
Question 8.


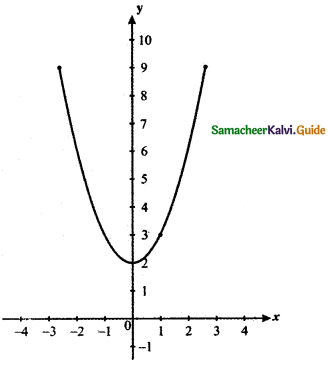
Answer:

From the graph the value of the function at x = 1 is y = f(1) = 3

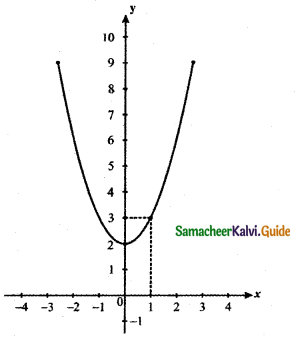
Question 9.


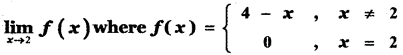
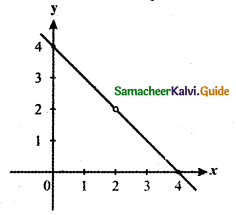
Answer:

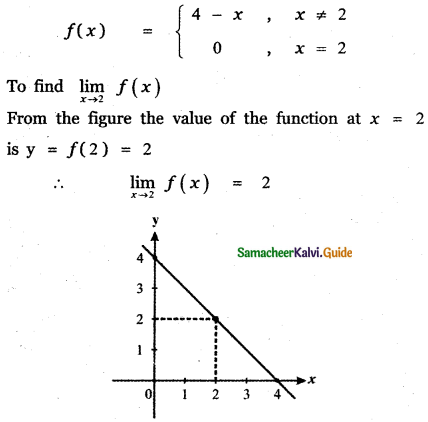
Question 10.


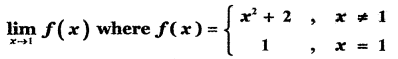
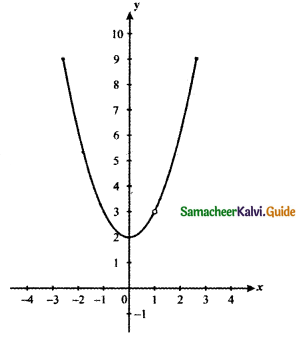
Answer:


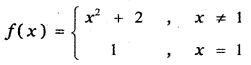
From the graph the value of the function is y = f(1) = 3

Question 11.


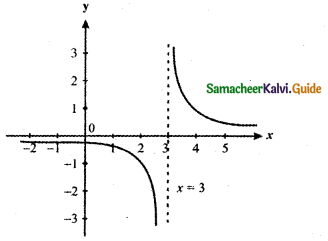
Answer:

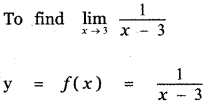
From the graph the value of the function at x = 3 the curve does not meet the line x = 3
∴ The value of the function is not defined at the point x = 3.
Hence \(\lim _{x \rightarrow 3} \frac{1}{x-3}\) does not exist at x = 3.

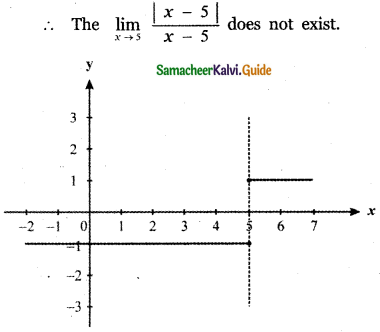
Question 12.

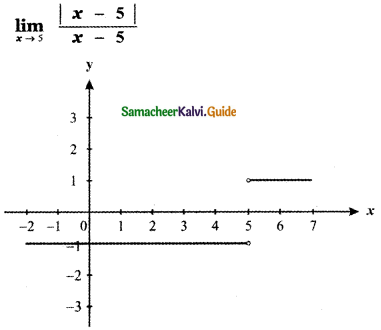
Answer:

From the graph x = 5 curve does not intersect the line x = 5
∴ The value of the function y = f(x) does not exist at x = 5.

Question 13.
\(\lim _{x \rightarrow 1}\) sin πx

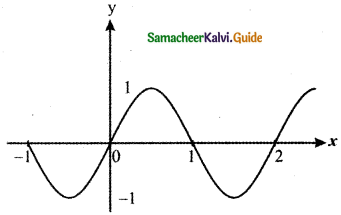
Answer:
\(\lim _{x \rightarrow 1}\) sin πx
From the graph x = 1, the curve y = f(x) intersects the line x = 1 at x – axis.
∴ y = f(1) = 0
Hence \(\lim _{x \rightarrow 1}\) sin πx = 0

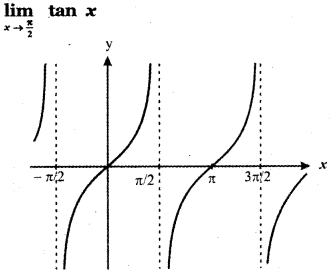
Question 14.
\(\lim _{x \rightarrow 0}\) sec x

Answer:
To find \(\lim _{x \rightarrow 0}\) sec x
Let y = f(x) = sec x
From the graph at x = 0 the curve intersect the y – axis.
At x = 0 we have y = 1
∴ \(\lim _{x \rightarrow 0}\) sec x = 1

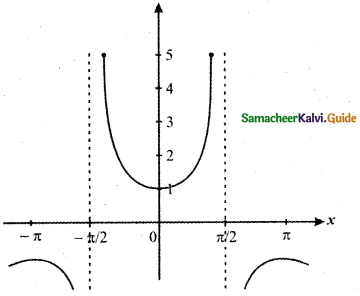
Question 15.

Answer:

y = f(x) = sec x
From the graph at x = \(\frac{\pi}{2}\), the curve does not intersect the line x = \(\frac{\pi}{2}\)
At x = \(\frac{\pi}{2}\), the value of the function y = f(x) does not exist.
Hence does not exist.

Sketch the graph of f, then identify the values of x₀ for which \(\lim _{x \rightarrow x_{0}}\) f (x) exists.

Question 16.

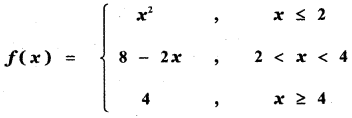
Answer:

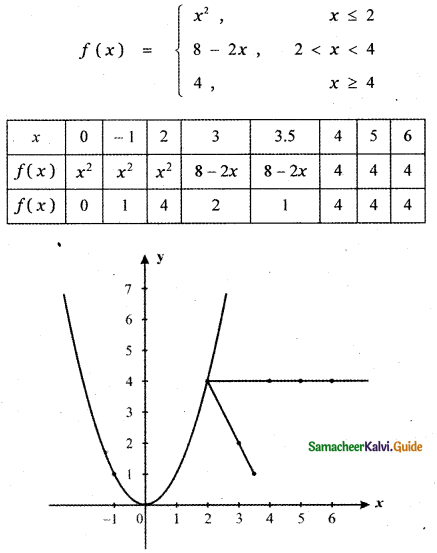
At x = 4 , the curve does not exist. Hence, except at x₀ = 4 , the limit of f(x) exists.

Question 17.

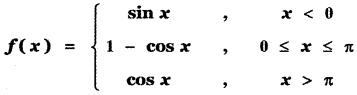
Answer:

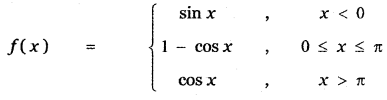
From the figure when x = π, y = f(π) = 2. The function is not defined at x = π since sin x lies in the interval [ – 1, 1]
∴ The given function has limits at all points except at x = π


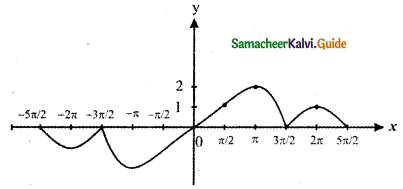
(π, 2) point is not possible since the range of the curve is [- 1 , 1] . Except x₀ = π, the curve has limits.

Question 18.
Sketch the graph of a function f that satisfies the given values:
(i) f(0) is defined
\(\lim _{x \rightarrow 0}\) f(x) = 4
f(2) = 6
\(\lim _{x \rightarrow 2}\) f(x) = 3
Answer:

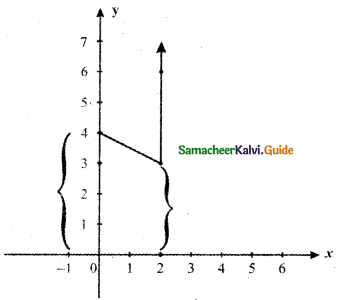
(ii) f(-2) = 0
f(2) = 0
\(\lim _{x \rightarrow-2}\) f(x) = 0
\(\lim _{x \rightarrow 2}\) f(x) does not exist.
Answer:

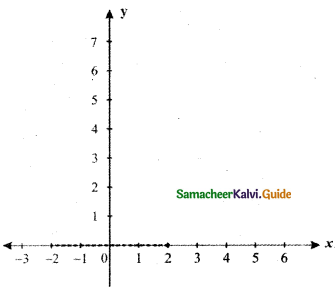
Question 19.
Write a brief description of the meaning of the notation \(\lim _{x \rightarrow 8}\) f(x) = 25
Answer:
Given \(\lim _{x \rightarrow 8}\) f(x) = 25
By the definition of limit

∴ f(8^–) = f(8⁺) = 25

Question 20.
If f(2) = 4, can you conclude anything about the limit of f (x) as x approaches 2?
Answer:
No, f(x) = 4, It is the value of the function at x = 2
This limit doesn’t exists at x = 2
Since f(2) = 4
It need not imply that \(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{+}} f(x)\)
∴ we cannot conclude at x = 2

Question 21.
If the limit of f (x) as x approaches 2 is 4, can you conclude anything about f (2)? Explain reasoning.
Answer:
\(\lim _{x \rightarrow 2}\) f(x) 4 , \(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) f(x) = 4
When x approaches 2 from the left or from the right f(x) approaches 4.
Given that \(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) f(x) = 4
The existence or non-existence at x =2 has no leaving on the existence of the limit of f(x) as x approaches to 2.
∴ We cannot conclude the value of f(2).

Question 22.

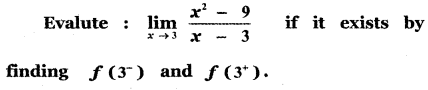
Answer:

Question 23.
Verify the existence of \(\lim _{x \rightarrow 0}\) f(x), where

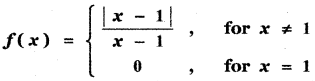
Answer:

From equations (1) and (2) we get
f(1^–) ≠ f(1⁺)
∴ The limit of f(x) does not exist.