Samacheer Kalvi 11th Physics Guide Chapter 3 Laws of Motion

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Physics Guide Pdf Chapter 3 Laws of Motion Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 3 Laws of Motion

11th Physics Guide Laws of Motion Book Back Questions and Answers

Part – I:
I. Multiple choice questions:

Question 1.
When a car takes a sudden left turn in the curved road, passengers are pushed towards the right due to _______.
a) inertia of direction
b) inertia of motion
c) inertia of rest
d) absence of inertia
Answer:
a) inertia of direction

Question 2.
An object of mass m held against a vertical wall by applying horizontal force F as shown in the figure. The minimum value of the force F is _______ (IIT JEE 1994)

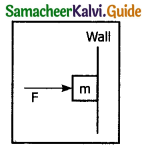
a) Less than mg
b) Equal to mg
c) Greater than mg
d) Cannot determine
Answer:
c) Greater than mg

Question 3.
A vehicle is moving along the positive x-direction, if a sudden brake is applied, then _______.
a) frictional force acting on the vehicle is along negative x-direction
b) frictional force acting on the vehicle is along the positive x-direction
c) no frictional force acts on the vehicle
d) frictional force acts in a downward direction
Answer:
a) frictional force acting on the vehicle is along the negative x-direction

Question 4.
A book is at rest on the table which exerts a normal force on the book. If this force is considered as a reaction force, what is the action force according to Newton’s third law?
a) Gravitational force exerted by Earth on the book
b) Gravitational force exerted by the book on Earth
c) Normal force exerted by the book on the table
d) None of the above
Answer:
c) Normal force exerted by the book on the table

Question 5.
Two masses m₁ and m₂ are experiencing the same force where m₁ < m₂. The ration of their acceleration a₁/a₂ is _______.
a) 1
b) less than 1
c) greater than 1
d) all the three cases
Answer:
c) greater than 1

Question 6.
Choose an appropriate free body diagram for the particle experiencing net acceleration along the negative y-direction. (Each arrow mark represents the force acting on the system).

Answer:

Question 7.
A particle of mass m sliding on the smooth double inclined plane (shown in the figure) will experience _______.

a) greater acceleration along the path AB
b) greater acceleration along the path AC
c) same acceleration in both the paths
d) no acceleration in both the paths
Answer:
b) greater acceleration along the path AC

Question 8.
Two blocks of masses m and 2m are placed on a smooth horizontal surface as shown. In the first case, only a force F₁ is applied from the left. Later only a force F₂ is applied from the right. If the force acting at the interface of the two blocks in the two cases is the same, then F₁ : F₂ is _______. (Physics Olympiad 2016)

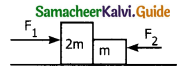
a) 1 : 1
b) 1 : 2
c) 2 : 1
d) 1 : 3
Answer:
c) 2 : 1

Question 9.
Force acting on the particle moving with constant speed is _______.
a) always zero
b) need not be zero
c) always non zero
d) cannot be concluded
Answer:
b) need not be zero

Question 10.
An object of mass m begins to move on the plane inclined at an angle θ. The coefficient of static friction of inclined surface is us. The maximum static friction experienced by the mass is _______.
a) mg
b) μ_s mg
c) μ_s mg sin θ
d) μ_s mg cos θ
Answer:
d) μ_s mg cos θ

Question 11.
When the object is moving at a constant velocity on the rough surface _______.
a) net force on the object is zero
b) no force acts on the object
c) only external force acts on the object
d) only kinetic friction acts on the object
Answer:
a) net force on the object is zero

Question 12.
When an object is at rest on the inclined rough surface _______
a) static and kinetic frictions acting on the object is zero
b) static friction is zero but kinetic friction is not zero.
c) static friction is not zero and kinetic friction is zero.
d) static and kinetic frictions are not zero.
Answer:
c) static friction is not zero and kinetic friction is zero.

Question 13.
The centrifugal force appears to exist _______.
a) only in inertial frames
b) only in rotating frames
c) in an accelerated frame
d) both in inertial and non-inertial frames
Answer:
b) only in rotating frames

Question 14.
Choose the correct statement from the following.
a) Centrifugal and centripetal forces are action-reaction pairs.
b) Centripetal forces is a natural force.
c) Centrifugal force arises from the gravitational force.
d) Centripetal force acts towards the center and centrifugal force appears to act away from the center in a circular motion.
Answer:
d) Centripetal force acts towards the center and centrifugal force appears to act away from the center in a circular motion.

Question 15.
If a person moving from pole to equator, the centrifugal force acting on him
a) increase
b) decreases
c) remains the same
d) increase and then decreases
Answer:
a) increase

II. Short Answer Questions:

Question 1.
Explain the concept of Inertia. Write two examples each for Inertia of motion, inertia of rest and inertia of direction.
Answer:
The inability of objects to move on its own or change its state of motion is called inertia. Inertia means resistance to change its state. There are three types of inertia:
1. Inertia of rest:
The inability of an object to change its state of rest is called inertia of rest.
Example:

• When a stationary bus starts to move, the passengers experience a sudden backward push.
• A book lying on the table will remain at rest until it is moved by some external agencies.

2. Inertia of motion:
The inability of an object to change its state of uniform speed (constant speed) on its own is called inertia of motion.
Example:

• When the bus is in motion, and if the brake is applied suddenly, passengers move forward and hit against the front seat.
• An athlete running is a race will continue to run even after reaching the finishing point.

3. Inertia of direction:
The inability of an object to change its direction of motion on its own is called inertia of direction.
Example:

• When a stone attached to a string is in whirling motion, and if the string is cut suddenly, the stone will not continue to move in circular motion but moves tangential to the circle.
• When a bus moving along a straight line takes a turn to the right. The passengers are thrown towards left.

Question 2.
State Newton’s second law:
Answer:
Newton second law state that” The force acting on an object is equal to the rate of change of its momentum:
F = \(\frac { dp }{ dt }\)
If m is the mass_of the object, and v its velocity of motion then \(\overline{p}\) = m\(\overline{v}\):
The above equation can be written as
F = \(\frac { dp }{ dt }\)(m\(\overline{v}\) ) = m\(\frac { dv }{ dt }\)
∴ F = ma

Question 3.
Define one newton:
Answer:
One newton is defined as the force which acts on 1 kg of mass to give an acceleration 1 ms^-2 in the direction of the force.

Question 4.
Show that impulse is the change of momentum.
Answer:
If a very large force acts on an object for a very short time, then the force is impulsive force or impulse. If a Force (F) acts on an object in a very short time (∆t), then from Newton’s second law dp = f.dt
Integrating \(\int_{i}^{f} d p=\int_{t_{1}}^{t_{2}} f d t\)
P_f – P_i =F[t₁ – t₂]
P_i – initial momentum of the object at time t₁
P_f – Final momentum of the object at time t₂
P_f – P_i = ∆P = > Change is momentum
(t₂ – t₁) = ∆t = > Time interval
The above equation can be written as
∴ ∆P = F ∆ t.
ie \(\int_{t_{1}}^{t_{2}} F d t\) = J is called the impulse and t₁ it is equal to change in momentum of the object is ∆P = F ∆ t. When F is kept constant

Question 5.
Using free body diagram, show that it is easy to pull an object than to push it.
Answer:
It is easier to pull on object than to push it.
An object pushed at a angle θ.

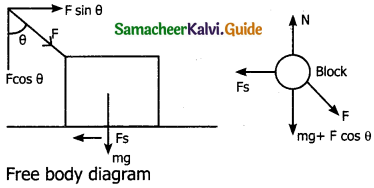
Case 1:
When a body is pushed at an arbitrary angle θ (0 to π/2) the applied force. F is resolved into two components
F sin θ = Horizontally – parallel to surface
F cos θ = Vertically – perpendicular to surface
The total downward force = mg + F cos 0 This is equal to normal force (reaction)
N_Push = mg + F cos θ … (1)
The static friction is equal to
P^s_(max) = μS N_push = μ_s (mg + F cos θ) … (2)

Case 2:
An object pulled at an angle θ

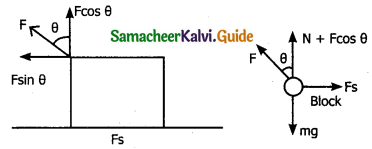
When an object is pulled at an angle 0 the applied force is resolved into two components.
F sin θ – Horizontally – parallel to the surface
F cos θ – Vertically – perpendicular to the surface
The total downward force = mg – F cos θ
This is equal to the normal force (reaction)
N_pull = mg – F cos θ … (3)
The static friction is equal to
F_s^(max) = μ_s N_pull = μ_s (mg – F cos θ) … (4)
Conclusion:
From equations (1) & (3) (or) from (2) and (4) it is clear that normal force or reaction due to pulling is less than that of push. So it is easier to pull an object than push it out.

Question 6.
Explain the various types of friction suggest a few methods to reduce friction.
Answer:
There are two types of Friction:
(1) Static Friction:
Static friction is the force which opposes the initiation of motion of an object on the surface. The magnitude of static frictional force f_s lies between
\(0 \leq f_{s} \leq \mu_{s} \mathrm{N}\)
where, µ_s – coefficient of static friction
N – Normal force

(2) Kinetic friction:
The frictional force exerted by the surface when an object slides is called as kinetic friction. Also called as sliding friction or dynamic friction,
f_k – µ_kN
where µ_k – the coefficient of kinetic friction
N – Normal force exerted by the surface on the object

Methods to reduce friction:
Friction can be reduced

• By using lubricants
• By using Ball bearings
• By polishing
• By streamlining

Question 7.
What is the meaning of “Pseudo force”?
Answer:
“A force which does not actually act on particles but appears due to acceleration of the frame is called – Pseudo force”. In order to use Newton I & II law in the rotational frame of reference, one needs to include a “Pseudo force” called “Centrifugal force”. A pseudo force has no origin, It arises due to the non-inertial nature of the frame considered. In order to solve circular motion problems from a rotating frame of reference, pseudo force is necessary.

Question 8.
State of the empirical laws of static and kinetic friction.
Answer:

Question 9.
State Newton’s third law.
Answer:
Newton’s third law states that for every action there is an equal and opposite reaction.

Question 10.
What are inertial frames?
Answer:
A frame of reference in which Newton’s I law of motion holds good is called an inertial frame of reference. In such a frame if no force acts on a body it continues to be at rest or in uniform motion. So it is called as an inertial frame.

Question 11.
Under what condition will a car skid on a leveled circular road?
Answer:
On a leveled circular road, if the static friction is not able to provide enough centripetal ’force to turn, the vehicle will start to skid \(\mu_{s}<\frac{v^{2}}{r g}\)

III. Long Answer Questions:

Question 1.
Prove the law of conservation of linear momentum. Use it to find the recoil velocity of a gun when a bullet is fired from it.
Answer:
Law: If there are no external forces acting on the system, then the total linear momentum of the system ( ^–_tot) is always a constant vector. In other words, the total linear momentum of the system is conserved in time.
Proof:
By combing Newton’s second and third laws the law of conservation of total linear momentum can be proved. When two particles interact with each other, they exert equal and opposite forces on each other
Consider two particles 1 & 2.
Let F₂₁ be the force exerted on 2 by 1
Let F₁₂ be the force exerted on 1 by 2
According to Newtons III law
\(\bar { F }\)₂₁ = – \(\bar { F }\)₁₂ → (1)
In terms of momentum, according to Newtons II Law,
F₁₂ = \(\frac { d }{ dt }\)\(\bar { P }\)₁ → (2)
F₂₁ = \(\frac { d }{ dt }\)\(\bar { P }\)₂ → (3)
Where is the momentum of p₁ particle P₂ is the momentum of II particle Sub (2) & (3) in (1)

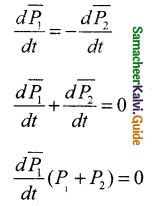
This implies that (P₁ + P₂) = constant vector
\(\bar { P }\)₁ + \(\bar { P }\)₂ = \(\bar { P }\)_tot– is the total linear momentum of the two particle system.
F₁₂ & F₂₁ are internal force and no external force acting on the system form outside. So total linear momentum is conserved.

Question 2.
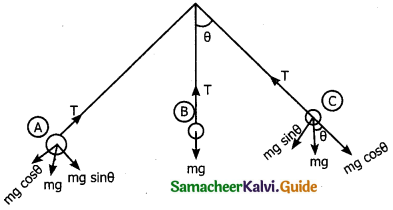
What are concurrent forces? State Lamis theorem.
Answer:
Concurrent forces:
A collection of forces is said to be concurrent if the lines of forces act at a common point. If the concurrent forces are in same plane they are coplanar also, in additional to concurrent forces.

Lamis is a theorem:
If a system of three concurrent and coplanar forces is in equilibrium, then Lamis theorem states that ” the magnitude of each force of the system is proportional to sine of the angle between other two forces”.

Proof:
Let F1, F2 and F3 be three coplanar and concurrent forces act at a common point 0 as in figure.

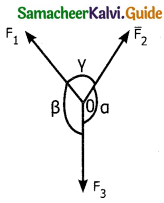
If the point 0 is in equilibrium then according to Lamis theorem.

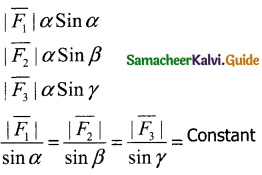
Question 3.
Explain the motion of blocks connected by a string in 1) vertical motion 2) horizontal motion.
Answer:
When blocks are connected by strings and force F is applied vertically or horizontally, it produces Tension (T) in the string which affects acceleration to some extent. Let us discuss vertical and horizontal motion here

Case 1:
1) Vertical motion of connected bodies:

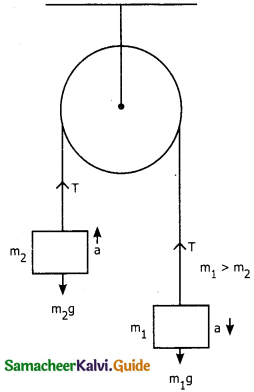
Consider two blocks to masses m₁ and m₂ (m₁ > m₂) connected by light and in an extensible string that passes over the pulley.

Let T be the tension in the string and a be the acceleration. When the system is released m₂ move vertically up and m₁ move vertically down with acceleration a. The gravitational force m₁g on m₁ is used to lift m₂. The upward direction is chosen as y. The free body diagram of both masses can be drawn as

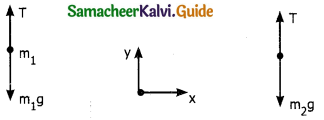
Applying Newton II law for mass m₂
T\(\hat{j}\) – m₂g\(\hat{j}\) = m₂a\(\hat{j}\) → (1)
By comparing the components on both sides We get
T – m₂g = m₂a
Similarly for mass m₁

If m₁ = m₂ ie both masses are equal, a = 0 This shows that if masses are equal, there is no acceleration, and the system as a whole will be at rest.

Tension on the string:
Substitute the value of ‘a’ from (4) in (1)

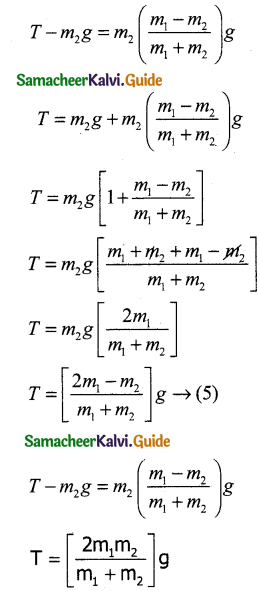
Equation (4) gives the magnitude of acceleration for m₁ the acceleration vector is
For m₁ the acceleration vector is

Case 2:
2) Horizontal motion of connected masses:
Let mass m₂ kept on the horizontal surface or table and m₁ is hanging through a small pulley.

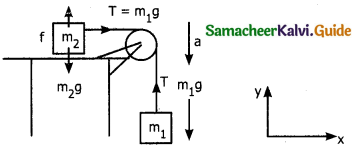
Assume there is no friction on the surface. As both the blocks are connected to the unstretchable string, m₁ moves with an acceleration downward then m₂ also moves with the same acceleration ‘a’ horizontally.

The forces acting on m₂ are

1. Downward gravitational force (m₂ g)
2. Upward normal force (N) exerted by the surface.
3. Horizontal Tension (T) exerted by the string.

Free body diagram

i) Downward gravitational force m₁g
ii) Tension ‘T’ – upwards.
Applying II Law for m₁.
T\(\hat{j}\) – m₁g\(\hat{j}\) = – m₁a\(\hat{j}\)
m₁g\(\hat{j}\) – T\(\hat{j}\) = m₁a\(\hat{j}\)
By comparing components
m₁g – T = m₁a → (1)
Apply Newton’s II Law for m₂
T\(\hat{i}\) = m₂a\(\hat{i}\) (along x)
Comparing components
N = m₂ → (2)
There is no acceleration along y direction
N = m₂a → (3)
Substituting (2) in (1)

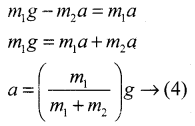
Tension can be got by substituting (4) in (2)

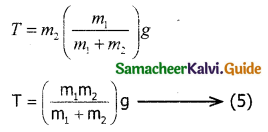
Conclusion: By comparing motion in both cases it is clear that the tension in the string for horizontal motion is half of the tension for vertical motion for same set of masses and strings.

Question 4.
Briefly explain the origin of friction show that in an inclined plane, angle of friction is equal to angle of repose.
Answer:
Frictional is an opposing force exerted by the surface on the object which resists it motion. This force is frictional force. Friction force always opposes the relative motion between two surfaces which are in contact.

“when a force parallel to the surface is applied on the object, the force tries to move the object with respect to the surface. This relative motion is opposed by the surface by exerting a frictional force on the objects in a direction opposite to the applied force. Frictional force always act on the object parallel to surface on which the object is placed”.

To show angle of repose = angle of friction in an inclined plane.

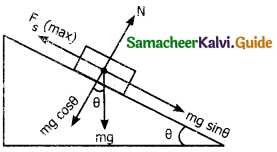
Angle of friction = tan θ = F_s/N
Consider an inclined plane on which an object is placed.
Let θ be the angle of inclination of the plane with horizontal.
“Angle of repose is the angle of inclined plane with horizontal such that an object placed on it begins to slide”.
The gravitational force mg is resolved into two components.
mg sin θ – parallel to inclined plane.
mg cos θ – perpendicular to inclined plane.
The component mg sin θ parallel to inclined plane tries to move the object down.
The component mg cos θ perpendicular to inclined plane is balanced by normal reaction N.
N = mg cos θ … (1)
When the object just begins to slide static friction attains its maximum value

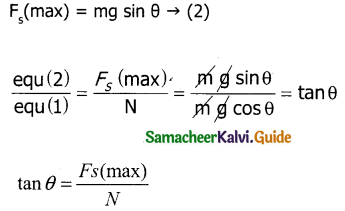
tan θ = angle of repose = angle of friction.
Which is equal to tan θ = μ_s
Hence proved.

Question 5.
State Newton’s three laws and discuss their significance.
Answer:

1. I law: Every object continues to be in the state of rest or off uniform motion unless there is external force acting on it.
2. II law: The force acting on an object is equal to the rate of change of its momentum F = \(\frac{d(\bar{p})}{d t}\)
3. III law: For every action there in an equal and an opposite reaction.

Discussion:
1) Newton’s laws are vector laws. The equation \(\bar { F }\) = \(\bar { ma }\) is a vector equation and it is essentially equal to three scalar equations. In Cartesian co-ordinate this equation can be written as
F_x\(\hat{i}\) + F_y\(\hat{i}\) + F_y\(\hat{k}\) = ma_x\(\hat{i}\) + ma_y\(\hat{j}\) + ma_z\(\hat{k}\) From this we can infer Fz cannot affect a_y and a_z and vice versa.

2) The acceleration experienced at a time ‘t’ depends on the force and the body at that instant does not depend on the force which acted on the body before F(t) = ma(t) In general direction of force may be different form direction of motion.

Case 1: Force and motion in same direction:
Example: when an apple falls towards earth the direction of motion and the force are in same downward direction.

Case 2: Force and motion are not in same direction
Example: The moon experiences a force towards the earth. But if actually moves in an elliptical orbit. In this case direction of motion and force are different.

Case 3: Force and motion in opposite direction:
If an object is thrown vertically upwards direction of motion is upward, but a gravitational force is downward.

Case 4: Zero net force, but there is motion:
Example: When a raindrop gets detached from the cloud it experiences both downward gravitational force and upward air drag force. As it descends the upward drag force increases and cancels the downward force. So the raindrop moves with a constant velocity called terminal velocity till it touches the surface of the earth, Hence the raindrop comes with zero net force and therefore with zero acceleration but with non zero terminal velocity.

Case 5: if multiple forces
\(\bar { F }\)₁, \(\bar { F }\)₂, \(\bar { F }\)₃, …… \(\bar { F }\)_n act on the same body, then the total force \(\bar { F }\) net is equal to vector sum of individual forces, which provides the acceleration.

\(\bar { F }\)_net = \(\bar { F }\)₁, \(\bar { F }\)₂, \(\bar { F }\)₃, …… \(\bar { F }\)_n
\(\bar { F }\)net = m\(\bar { a }\)
Example: Bow & arrow

Case 6: Newtons II Law can be written as
F = m\(\frac { dv }{ dt }\) = m.\(\frac{d^{2} r}{d t^{2}}\)
Newtons II law is basically a second order derivative of position vector, which is not zero, there must be a force acting on it.

Case 7: if no force acts an a body then
m. \(\frac{d \bar{v}}{d t}\) = 0
Which implied \(\bar { V }\) = constant. If is essentially a I law. So Newtons II law is consistent with I law, but cannot be derived form each other. Newton II law is a cause and effect relation. Force is the cause and effect is the acceleration,
(effect) ma = F(cause)
\(\frac{d \bar{p}}{d t}\) = F.

Question 6.
Captain the similarities and differences of between centripetal and centrifugal forces.
Answer:

Question 7.
Briefly explain centrifugal force with suitable examples.
Answer:
Circular motion can be analyzed from two different frames of reference. One is the Inertial frame where Newton’s laws are obeyed. The other is the rotating frame of reference which is noninertial as it is accelerating. To use Newton’s I and II law in the rotational frame of reference the pseudo force called as centrifugal force is needed.

The centrifugal forces appear to act on objects with respect to rotating frames. To explain consider an example, In the case of a whirling motion of a stone tied to a string, assume the stone has angular velocity ω in an inertial frame. If the motion of the stone is observed from a frame which is also rotating along with the stone with the same angular velocity ω then the stone appears to be at rest.

This implies that in addition to the inward centripetal force (-mrω²) there must be an equal and opposite force that acts on outwards equal to (+ mrω₂). So the total force acting on the stone in the rotating frame is equal to zero (- mrω² + mrω² = 0) This outward force acting on the stone + mrω² is called centrifugal force.

Question 8.
Briefly explain ‘rolling friction’.
Answer:
When an object moves on a surface essentially it is sliding on it. But the wheels move on the surface through rolling motion. In case of rolling motion when a wheel moves on a surface the point of contact is always at rest. Since the point of contact is at rest, there is no relative motion between the wheel and the surface. Hence the frictional force is very less.

At the same time if an object moves without a wheel, there is a relative motion between the object and the surface. As a result frictional force is larger. This makes it difficult to move the object.

Ideally in pure rolling, motion of point of contact with the surface should be at rest, but in practice it is not so. Due to elastic nature of the surface at the point of contact there will be same deformation on the wheel or on the surface. Due to this deformation there will be minimal friction between wheel and surface. It is called rolling friction. In fact rolling friction if much smaller than kinetic friction.

Question 9.
Describe the method of measuring angle of repose.
Answer:
Angle of repose is the minimum angle that an inclined plane makes with horizontal when a body placed on it just begins to slide. Consider a body of mass m placed on an inclined plane. The angle of inclination 0 of the inclined plane is adjusted that the body on the plane begins to slide down. Thus 0 is the angle of repose.

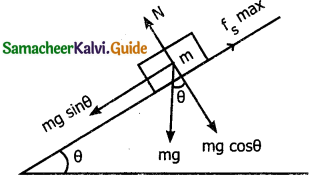
Various forces acting on the body are:
(a) Weight mg of the body acting vertically downwards

(b) The limiting friction fs (max) in upward direction along the inclined plane. It balances the component mg sin θ of the weight mg along the inclined plane.
∴ mg sin θ = f_s(max) …. (1)

(c) The normal reaction ‘N’ perpendicular to the inclined plane. It is balanced by the component mg cos θ, perpendicular to the inclined plane.

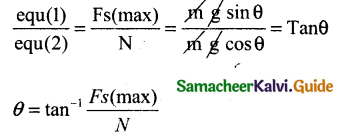
Where θ is the angle of repose.

Question 10.
Explain the need for banking of tracks.
Answer:
In a leveled circular road skidding mainly depends on the co-efficient of static friction n_s. The coefficient of static friction depends on the nature of surface which has a maximum limiting value. To avoid this usually “the outer edge of the road is slightly raised compared to inner edge”. This is called banking of roads or tracks. The angle of inclination called banking angle.

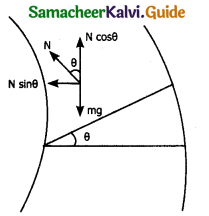
Let the surface of the road make angle θ with horizontal surface. Then the normal force makes an angle θ with vertical. When the car takes a turn, two forces are acting on the car.
(a) Gravitational force mg (downwards)
(b) Normal force N (Perpendicular to surface).
Normal force ‘N’ can be resolved into two components N cos θ and N sin θ and balances downward gravitational force.
N sin θ provides necessary centripetal acceleration, According to II law
N cos θ = mg
N sin θ = \(\frac{m v^{2}}{r}\)
Dividing the above equations,
tan θ = \(\frac{v^{2}}{r g}\)
V = \(\sqrt{r g \tan \theta}\)
∴ The banking angle θ and radius of curvature of the road or track determines the safe speed of car at the turning.
If the speed exceeds this safe limit, then it starts to skid outward but the frictional force comes into effect and provides an additional centripetal force to prevent outward skidding. But at the same time if the speed is less than the safe limit it starts to skid inward and again frictional force come into effect which reduces centripetal force to prevent inward skidding

However if the speed of the vehicle is sufficiently greater than the correct speed the frictional force cannot stop the car from skidding. So to avoid skidding in circular road or tracks they are banked.

Question 11.
Calculate the centripetal acceleration of moon towards the earth.
Answer:
The moon orbits the earth once in 27.3 days in an almost circular orbit.
Radius of earth = 6.4 x 10⁶ m.

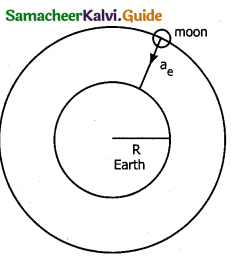
Solution:
The centripetal accelerations given by a = \(\frac{ v^{2}}{r}\)
This can be related with moon a_m = R_mω²
ω → angular velocity
a_m → centripetal acceleration of the moon due to earths gravity to angular velocity
R_m → Distance between the center of earth to moon. Which is 60 times the radius of the earth.

IV. Conceptual Questions:

Question 1.
Why it is not possible to push a car from inside?
Answer:
While trying to push a car from outside, he pushes the ground backward at an angle. The ground offers an equal reaction in the opposite direction, so car can be moved. But the person sits inside means car and the person becomes a single system, and the force given will be a internal force. According to Newton’s third law, total internal force acting on the system is zero and it cannot accelerate the system.

Question 2.
There is a limit beyond which the polishing of a surface increases frictional resistance rather than decreasing it. Why?
Answer:
When surfaces are highly polished the area of contact between them increases. As result of this a large number of atoms and molecules lying on both surfaces start exerting strong attractive forces on each other. Therefore the frictional force increases.

Question 3.
Can a single isolated force exist in nature? Explain your answer?
Answer:
No. According to Newton’s third law, for every action, there is an equal and opposite reaction. So, whatever case we consider, if there is an action there is always a reaction. So it is impossible.

Question 4.
Why does a parachute descend slowly?
Answer:
When a parachute is descending down in the atmosphere an equal and opposite force to motion of parachute is acting due to air resistance. As the area of the parachute is large the air resistance resists the motion and so it descends slowly.

Question 5.
When walking on ice one should take short steps. Why?
Answer:
When a person is walking on ice he presses the ice downward with his feet and in turn the ice pushes the person with an equal force. Since ice slippery the person is not able to press it hardly. So the action legs and so the reaction which is also less. So by making small steps, with larger normal force one can walk without slipping.

Question 6.
When a person walks on a surface the frictional force exerted by the surface on the person is opposite to the direction of motion. True or false.
Answer:
False. In frictional force exerted by the surface on the person is in the direction of his motion. The frictional force acts as an external force to move the person. When the person trying to move, he gives a push to ground on the backward direction and by Newton’s third law he is pushed by the ground in the forward direction. Hence frictional force acts along the direction of motion.

Question 7.
Can the coefficient of friction be more than one?
Answer:
No, it cannot be more than 1 for normal plane surfaces. But when surfaces are so irregular that they have sharp minute projections and cavities on them. Then the coefficient of friction may be more than one.

Question 8.
Can we predict the direction of motion of a body from the direction of force on it?
Answer:
Yes. The direction of motion is always opposite to the force of kinetic friction. By using the principle of equilibrium, the direction of force of static friction can be determined. When the object is in equilibrium, the frictional force must point in the direction which results as a net force is zero.

Question 9.
The momentum of a system of particles is always conserved. True or false.
Answer:
True: The Linear momentum of the system is always a constant vector, as long as no external force are acting on it.

V. Numerical Problems:

Question 1.
A force of 50N acts on the object of mass 20kg shown in the figure. Calculate the acceleration of the object in x and y-direction.

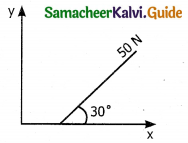
Solution:
m = 20kg, F = 50N
Force can be resolved into 2 components.
m = 20kg
F_x = F cos θ = 50 cos 30 = \(\frac{50 \sqrt{3}}{2}\)\(\frac { 1 }{ 2 }\)
F_y = F sin θ = 50 sin 30 = 50 x \(\frac { 1 }{ 2 }\) = 25N

Question 2.
A spider of mass 50 g is hanging on a string of a cobweb as shown in the figure. What is the tension in the string?
Solution:

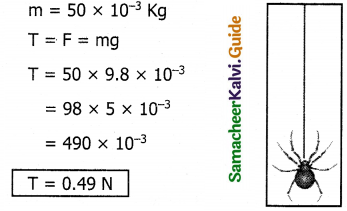
Question 3.
What is the reading shown in spring balance?
Solution:

∵ Forces on both sides are equal the reading in the spring balance is zero.

(ii)

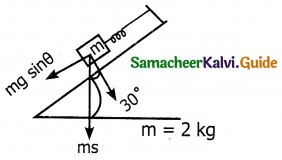
The spring is pulled by a force along the inclined plane so.
F = mg sin θ
= 2 x 9.8 x sin 30
= 9.8 x 2 x 1/2
F = 9.8 N

Question 4.
The physics books are stacked on each other in the sequence +1 volumes 1 and 2, +2 volumes 1 and 2 on a table, a) identify the forces acting on each book and draw the free body diagram, b) Identify the forces exerted by each books on the other.
Solution:

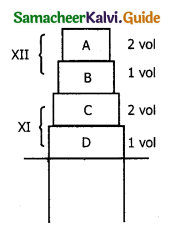
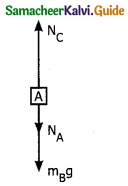
Force on book A
1) Downward gravitational force exerted by earth (m_A g)
2) Upward normal force (N_B) exerted by book B (N_B).

Force on book B
i) Downward gravitational force exerted by earth (m_B g)
ii) Downward force exerted by books A (N_A)
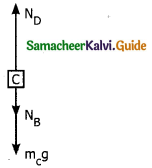
iii) Upward normal force exerted by book C (Nc).

Force on book C
i) Downward gravitational force exerted by earth (m_C g)
ii) Downward force exerted by books B (N_B)
iii) Upward normal force exerted by book D (N_D).

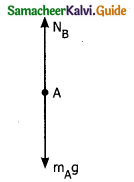
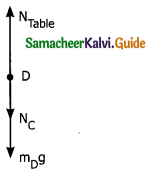
Force on book D

i) Downward gravitational force exerted by earth (m_D g)
ii) Downward force exerted by books C (N_c)
iii) Upward force exerted by the N_Table.

Question 5.
A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob into components. What is the acceleration experience by the bob at an angle 0?
Solution:

(i) Gravitational force(mg) acting downwards.
(ii) Tension (T) exerted by the string on the bob whose position determines the direction of T.
The bob is moving is a circular arc and so it has centripetal acceleration. At points A and C bob comes to rest momentarily and then its velocity increases when move towards B.
Hence tangential acceleration is along the arc.

The gravitational force can be resolved into two components.
mg cos θ along the string
mg sin θ perpendicular to the string
At point A & C T=mg cos θ and at all other points T is greater than mg cos θ.
∴ Centripetal force = T – mg cos θ
∴ ma_c = T- mg cos θ
Centripetal acceleration
a_c = \(\frac { T – mg cos θ}{ 2 }\)m

Question 6.
Two masses m₁ and m₂ are connected with a string passing over a frictionless pulley fixed at the corner of the table as shown in the figure. The coefficient of static friction of mass m₁ with the table is µ_s. Calculate the minimum mass m₃ that may be placed on m₁ to prevent it from sliding. Check if m₁ = 15kg, m₂ = 10kg, m₃ = 25kg and µ_s = 0.2.

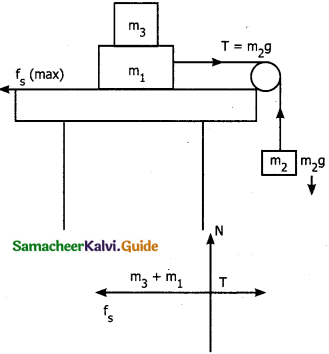
Solution:
(1) The mass m₁ and m₂ provides maximum static friction on the table
fS_(max) = µ_sN
= µ_s(m₁ + m₃)g
fS_(max) = 0.2(m₁ + m₃)g …. (1)
Tension T in the string provided by
= T = m₂g …. (2)
T < fs_(max) then m₁ and m₂ won’t move.
If m₃ is not present
T = fs (for just sliding)
When m₃ is placed on m₁ it won’t slide

(2) If m₁ = 15kg
m₂ = 10kg
m₃ = 25kg
µ_s = 0.2.
Then µ(m₁+m₃)g = 0.2(15±10)g
= 2.5 x 0.2g = 5 g =5g N
= 5g N
But m₂ g = 10g N
∵ m₂g = 10g N = T >µ_s(m₁ + m₃)g
∵ T > µs (m₁ + m₃)
m₁ + m₃ will slide on the table.

Question 7.
Calculate the acceleration of the bicycle of mass 25 kg as shown in fig 1 & 2.

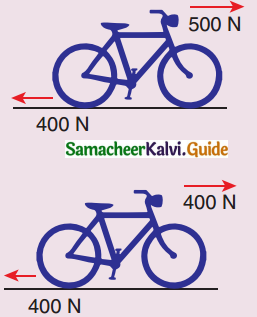
Solution:
Case 1:
Resultant force =
forward force – Frictional force
= 500 – 400
F_R = 100N
F_R = ma = 100N
a = \(\frac { 100 }{ 25 }\)
a = 4 ms^-2

Case 2:
Resultant force = forward force – Frictional force = 400 – 400 = 0 N
a = 0.

Question 8.
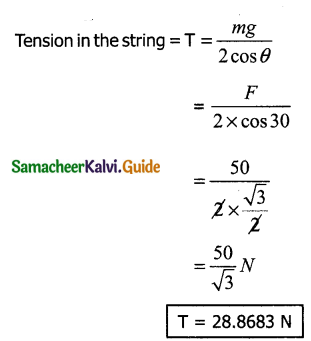
Apply Lamis theorem on sling shot and calculate the Tension in each string?

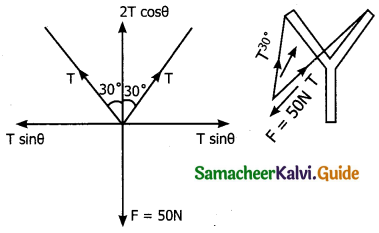
Solution:

Question 9.
A foot ball player kicks a 0.8 kg ball and imparts it a velocity 12 ms^-1. The contact between foot and ball is only for one sixtieth of a second find the average kicking force.
Solution:
m = 0.8 kg
v = 12 ms^-1
t = \(\frac { 1 }{ 60 }\)S
F = ?
Change in momentum = impulse
P_f – P_i = F_t
mv – 0 = Ft

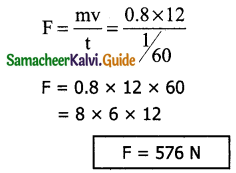
Question 10.
A stone of mass 2kg is attached to a string of length 1m. The string can withstand a maximum tension of 200N, What is the maximum speed that stone can have during the whirling motion.
Solution:
m = 2 kg
I = 1 m = r
T = F = 200 N
V = ?
During whirling motion, the force acting on the stone is a centripetal force which provides the necessary Tension in the string.
T = F = \(\frac{m v^{2}}{r}\)
200 = \(\frac{2 \times v^{2}}{1}\)
V_max = 10 ms^-1

Question 11.
Imagine that the gravitational force between Earth and Moon is provided by an invisible string that exists between the Moon and Earth. What is the tension that, exists in this invisible string due to earth’s centripetal force?
Solution:
Mass of moon = 7.34 x 10²² kg
Distance between the moon and earth = 3.84 x 10⁸ m

Question 12.
Two bodies of masses 15kg and 10kg are connected with light string kept on a smooth surface. A horizontal force F = 500N is applied to a 15kg as shown in the figure. Calculate the tension acting in the string.
Answer:

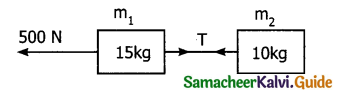
Let m₁ = 15kg
m₂ = 10kg
F = 500N
All the two blocks move with a common acceleration (a) under the force F = 500 N.
F = (m₁+m₂)

Question 13.
People often say “for every action there is an equivalent opposite reaction”. Here they meant ‘action of a human’. Is it correct to apply Newton’s third law to human actions? What is mean by ‘action’ in Newton’s third law? Give your arguments based on Newton’s laws.
Solution:
Newton’s third law is applicable to only humans actions that involve physical force. Third law is not applicable to humans’ psychological actions or thoughts.

Question 14.
A car takes a turn with velocity 50ms^-1 on the circular road of the radius of curvature 10m. Calculate the centrifugal force experienced by a person of mass 60kg inside the car?
Solution :
V = 50 ms^-1
r = 10m
centrifugal reaction = ?
m = 60kg
F = \(\frac{m v^{2}}{r}\)
= \(\frac { 60×50×50 }{ 10 }\)
= 3 x 5 x 10³
F = 15,000 N

Question 15.
A long stick rests on the surface. A person standing 10m away from the stick with what minimum speed an object of mass 0.5 kg should he threw so that it hits the stick. (Coefficient of kinetic friction is 0.7)

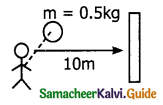
Solution:
Force on the mass = μ_kN = μ_k mg
F = 0.7 x 0.5 x 9.8
F = 3.43 N
But F = ma
a = \(\frac { 3.43 }{ 0.5 }\)
= 6.86ms^-2
m = 0.5kg
W.K.T
v² – u² = 2as
|u²| = 2as
u = \(\sqrt{2 \times 6.86 \times 10}\)
= 11.71 ms^-2
Velocity with which the mass is thrown = 11.71 ms^-1

11th Physics Guide Laws of Motion Additional Important Questions and Answers

I. Multiple choice questions:

Question 1.
The concept “force causes motion” was given by –
(a) Galileo
(b) Aristotle
(c) Newton
(d) Joule
Answer:
(b) Aristotle

Question 2.
A body of 5 kg is moving with a velocity of 20m/s. If a force of 100 N is applied on it for 10s in the same direction as its velocity, what will now be the velocity of the body _______.
a) 2000 m/s
b) 220 m/s
c) 240 m/s
d) 260 m/s
Answer:
b) 220 m/s

Question 3.
The inability of objects to move on their own or change their state of motion is called as –
(a) force
(b) momentum
(c) inertia
(d) impulse
Answer:
(c) inertia

Question 4.
A force vector applied on a mass is represented as \(\vec { f }\) = 6\(\vec { i }\) – 8\(\vec { j }\) + 10\(\vec { k }\) and accelerates with 1ms^-2, what will be the mass of the body in kg _______.
a) 10\(\sqrt{2}\)
b) 20
c) 2\(\sqrt{10}\)
d) 10
Answer:
a) 10\(\sqrt{2}\)

Question 5.
A particle of mass m is at rest at the origin at time t = 0. It is subjected to force F(t)= F₀e^-bt in the x direction. Its speed v(t) is depicted by which of the following curves?

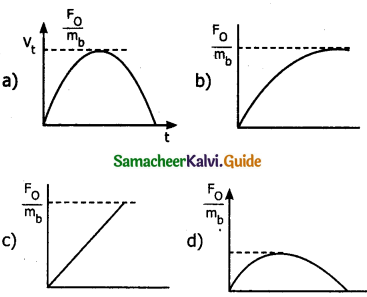
Answer:

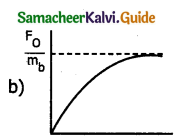
Question 6.
If the brake is applied in the moving bus suddenly, passengers move forward is an example for –
(a) Inertia of motion
(b) Inertia of direction
(c) Inertia of rest
(d) back pull
Answer:
(a) Inertia of motion

Question 7.
Two masses m₁ and m₂ are connected by a light string passing over a smooth pulley. When set free m₁ moves down by 2m in 2s the ratio of m₁/m₂ is _______.
a) 9/7
b) 11/ 9
c) 13/11
d) 15/13
Answer:
b) 11/ 9

Question 8.
Two blocks are connected by a string as shown in the figure. The upper block is hung by another string. A force ‘F’ applied on the upper string produces an acceleration of 2ms^-2. in the upward direction in both the blocks. If T and T¹ in both parts of the string then _______.

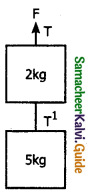
a) T = 84N; T¹ = 50N
b) T = 70N; T¹ = 70N
c) T = 84N; T¹ = 60N
d) T = 70N; T¹ = 60N
Answer:
c) T = 84N; T¹ = 60N

Question 9.
Four identical blocks each of mass m linked by threads as shown. IF the system moves with constant acceleration under the influence of force F, the Tension T² _______.

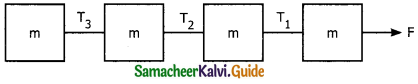
a) F
b) F/2
c) 2F
d) F/4
Answer:
b) F/2

Question 10.
Rate of change of momentum of an object is equal to –
(a) acceleration
(b) work done
(c) force
(d) impulse
Answer:
(c) force

Question 11.
A block of mass 10 kg is pushed on a smooth inclined plane of inclination 30°, so that it has an acceleration 2ms^-2. The applied force is _______.
a) 50 N
b) 60 N
c) 70 N
d) 80 N
Answer:
c) 70 N

Question 12.
Two blocks of masses 6 kg and 3 kg are connected by the string as shown over a frictionless pulley. The acceleration of the system is _______.

a) 4 ms^-2
b) 2 ms^-2
c) Zero
d) 6 ms^-2
Answer:
c) Zero

Question 13.
The acceleration of the systems shown in the figure is _______.

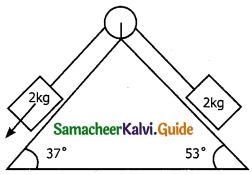
a) 1 ms^-2
b) 2 ms^-2
c) 3 ms^-2
d) 4 ms^-2
Answer:
a) 1 ms^-2

Question 14.
A uniform rope of length L is pulled by constant force P as shown, The Tension in the rope at a distance x from the end where the force is applied _______.

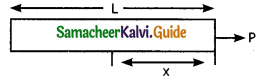
a) P
b) p[a – \(\frac { x }{ L }\) ]
c) px/L
d) p(1 + \(\frac { x }{ L }\) )
Answer:
b) p[a – \(\frac { x }{ L }\) ]

Question 15.
The law which is valid in both inertial and non-inertial frame is –
(a) Newton’s first law
(b) Newton’s second law
(c) Newton’s third law
(d) none
Answer:
(c) Newton’s third law

Question 16.
One end of a string of length / is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v the net force on the particle (directed towards centre) is _______.
a) T
b) T – \(\frac{m v^{2}}{r}\)
c) T + \(\frac{m v^{2}}{r}\)
d) 0
Answer:
a) T

Question 17.
A block is kept on a frictionless inclined surface with the angle of inclination α. The incline is given an acceleration ‘a’ to keep the block stationary. Then a is equal to _______.

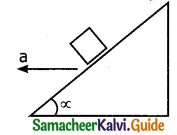
a) g
b) g tan α
c) g / tan α
d) g cosec α
Answer:
b) g tan α

Question 18.
The action and reaction forces acting on –
(a) same body
(b) different bodies
(c) either same or different bodies
(d) none of the above
Answer:
(b) different bodies

Question 19.
If an elevator moving vertically up with an acceleration g, the force entered on the floor by a passenger of mass M is _______.
a) mg
b) 1 / 2 mg
c) zero
d) 2 mg
Answer:
d) 2 mg

Question 20.
A man of weight 80 kg, stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of 5 ms^-2. What would be the reading on the scale? [g = 10 ms^-2].
a) 400 N
b) 1200 N
c) 800 N
d) zero
Answer:
b) 1200 N

Question 21.
A person is standing in an elevator in which situation he find his weight more than the actual weight _______.
a) the elevator moves upwards with constant acceleration
b) the elevator moves downwards with constant acceleration
c) the elevator moves upwards with uniform velocity
d) the elevator moves downwards with uniform velocity
Answer:
b) the elevator moves downwards with constant acceleration

Question 22.
Newton’s second law gives –
(a) \(\overrightarrow{\mathrm{F}} \propto \frac{d \overrightarrow{\mathrm{P}}}{\mathrm{dt}}\)
(b) \(\overrightarrow{\mathrm{F}}=\frac{d \overrightarrow{\mathrm{P}}}{\mathrm{dt}}\)
(c) \(\overrightarrow{\mathrm{F}}=m \vec{a}\)
(d) all the above
Answer:
(d) all the above

Question 23.
A mass of 1 kg is suspended by a string. Another string C is connected to its lower end (as in the figure). If a sudden jerk is given to c, then _______.

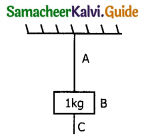
a) The portion AB of the string break
b) The portion BC of the string will break
c) The mass will be rotating
d) none of the above
Answer:
a) The portion AB of the string break

Question 24.
In the above questions, if the string c is stretched slowly then _______.
a) The portion AB of the string break
b) The portion BC of the string will break
c) The mass will be rotating
d) none of the above
Answer:
a) The portion AB of the string break

Question 25.
As shown in the figure, the tension in the horizontal card is 30N. The weight w and the tension in the string OA in Newton are _______.

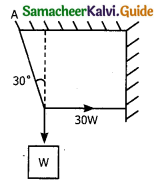
a) 30, \(\sqrt{3}\), 30
b) 30\(\sqrt{3}\), 60
c) 60\(\sqrt{3}\), 30
d) none of the above
Answer:
b) 30\(\sqrt{3}\), 60

Question 26.
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms^-1. How long does the body take to stop?
(a) 0.75 s
(b) 1.33 s
(c) 6 s
(d) 35 s
Answer:
Acceleration a = \(\frac{-F}{m}\) = \(\frac{50}{20}\) = – 2.5 ms^-2
u = l5 ms^-1
v = 0
t = ?
v = u + at
0 = 15 – 2.5t
t = \(\frac{15}{2.5}\) = 6s

Question 27.
A block of mass 10 kg is suspended through two light spring balances as in figure.

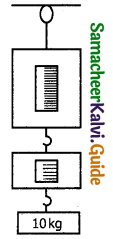
a) both scales will read 10 kg
b) both scales will read 5 kg
c) the upper scale will read 10 kg and the lower zero
d) the reading may be anything but their sum will be 10 kg
Answer:
a) both scales will read 10 kg

Question 28.
Two blocks A and B of masses 2m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as in figure. The magnitude of the acceleration of A and B after the string is cut, are respectively.

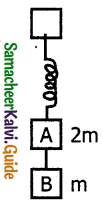
a) g, g/2
b) g/2, g
c) g, g
d) g/2, g/2
Answer:
b) g/2, g

Question 29.
Choose the correct statement _______.
a) The frictional forces are dependent on the roughness of the surface.
b) The kinetic friction is proportional to normal reaction
c) The friction is independent of area of contact
d) All statements are correct
Answer:
d) All statements are correct

Question 30.
When an object of mass m slides on a frictionless surface inclined at an angle θ, then the normal force exerted by the surface is-
(a) g cos θ
(b) mg cos θ
(c) g sin θ
(d) mg tan θ
Answer:
(b) mg cos θ

Question 31.
Two cars of unequal masses are similar types. If they are moving at the same initial speed, the minimum stopping distance _______.
a) is smaller for the heavier car
b) is smaller for the lighter car
c) is same for both car
d) depends on volume of the car
Answer:
c) is same for both car

Question 32.
An ice block is kept on an inclined plane of angle of 30°. The coefficient of kinetic friction between the block and the inclined plane is \(\frac{1}{\sqrt{3}}\). The acceleration of the block is _______.
a) zero
b) 2 ms^-2
c) 1.5 ms^-2
d) 5 ms^-2
Answer:
d) 5 ms^-2

Question 33.
Starting from rest a body slides down at 45° inclined plane in twice the time, it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is __________.
a) 0.33
b) 0.25
c) 0.75
d) 0.80
Answer:
c) 0.75

Question 34.
A uniform metal chain if placed on a rough table such that the one end of the chain hangs down over the edge of the table. When one-third of its length hangs over the edge, the chain starts sliding. Then the coefficient of static friction is _______.
a) 3/4
b) 1/4
c) 2/3
d) 1/2
Answer:
d) 1/2

Question 35.
If two masses m₁ and m₂ (m₁ > m₂) tied to string moving over a frictionless pulley, then the acceleration of masses –
(a) \(\frac{\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\) g
(b) \(\frac{m_{1}+m_{2}}{\left(m_{1}-m_{2}\right)}\) g
(c) \(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\) g
(d) \(\frac{m_{1} m_{2}}{2 m_{1} m_{2}}\) g
Answer:
(a) \(\frac{\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\) g

Question 36.
While walking on ice one should take small steps to avoid slipping. This is because smaller steps ensure _______.
a) large friction
b) smaller friction
c) larger normal force
d) smaller normal force
Answer:
c) larger normal force

Question 37.
A box is placed on inclined plane and has to be pushed down. The angle of inclination is _______.
a) equal to angle of friction
b) more than angle of friction
c) equal to angle repose
d) less than angle of repose
Answer:
d) less than angle of repose

Question 38.
Three masses in contact is as shown above. If force F is applied to mass m₁ then the contact force acting on mass m₂ is –
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
(b) \(\frac{m_{1} F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(c) \(\frac{\left(m_{2}+m_{3}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(d) \(\frac{m_{3} \mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
Answer:
(c) \(\frac{\left(m_{2}+m_{3}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}\)

Question 39.
A block B is placed on block A. The mass block B is less than the mass of block friction that exists between the blocks whereas the ground on which block A is placed is taken to be smooth. A horizontal force ‘F’ increasing linearly with time beings to act on B. The acceleration a_A and a_B of blocks A and B respectively are plotted against Y. The correctly plotted graph is _______.

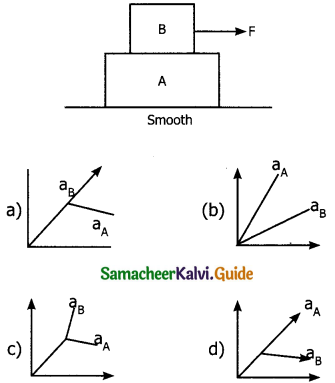
Answer:

Question 40.
Two blocks of mass m₁ 6 kg and m₂ = 3 kg as in figure coefficient of friction between m₁, and m₂ and between m₁ and surface is 0.5 and 0.4 respectively. The maximum horizontal force to can be applied to the mass m₁ so that they move without separation is _______.

a) 41 N
b) 61 N
c) 81 N
d) 101 N
Answer:
c) 81 N

II. Additional Questions:

Question 1.
Identify the internal and external forces acting on the following systems.
a) Earth alone as a system
b) Earth and sun as a system
c) Our body as a system white walking
d) our body and earth as a system
Solution:
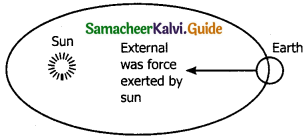
(a) Earth alone as a system:

Earth orbits the sun due to the gravitational attraction of the sun. If we consider earth as a system, then the sun’s gravitational force is an external force. If the moon is also taken into account, it also exerts an external force on earth.

(b) (Earth + sun) as a system:

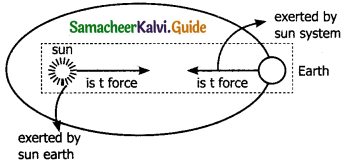
In this case, there are two internal forces which form action and reaction pair, i.e gravitational force on the sun by earth & vice versa.

(c) Our body as a system:
While walking, we exert a force on earth and earth exerts an equal and opposite force on our body. If our body is considered as a system then the force exerted by the earth on our body is external.

(d) Our body + earth as a system.
In this case, there are two internal forces present in the system one is the force exerted by our body on earth and the other is the equal and opposite force exerted by the earth on our body.

Question 2.
When a cricket player catches the ball he pulls his hands gradually is the directions of the ball’s motion. Why?
Answer:
If the man stops his hands soon after catching the ball the ball comes to rest quickly. It means that the momentum of the ball is brought to rest very quickly. So the average force acting on the body will be very large. Due to the large average force, the hands will get hurt. To avoid this the player brings the ball to rest slowly.

Question 3.
An impulse is applied to a moving object with a force at an angle of 20° w.r.t. velocity vector, what is the angle between the impulse vector and change in momentum vector?
Answer:
Impulse and change in momentum are in the same direction. Therefore the angle between these two vectors is zero.

Question 4.
Why a high jumper after crossing the bar made to fall on a spongy floor instead of the cemented floor.
Answer:
After high jumping, landing on a cemented floor is more dangerous than jumping on a spongy surface. A spongy surface brings the body to rest slowly than the cemented floor So that the average force experienced by the body will be lesser.

Question 5.
Obtain an expression for centrifugal force acting on a man on the surface of the earth.
Answer:

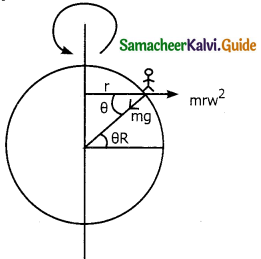
Even though earth is treated as an inertial frame, it is actually not so. Earth spins about its own axis with an angular velocity co Any object at the surface of the earth (rotational frame) experiences a centrifugal force. The centrifugal force appears to act exactly in opposite direction from the axis of rotation.

The centrifugal force on a man standing on the surface of earth is = mrω² where r is the perpendicular distance of man from the axis of rotation. From fig. r = R cos θ where R= radius of earth.
θ = latitude of the earth where man is standing

Question 6.
A stone when thrown on a glass window smashes the window pane to pieces, but a bullet from the gun passes through, by making a clean hole. Why?
Answer:
Due to small speed the stone remains in contact with the window pane for a long time. It transfer its motion to the pane and break them into pieces. But the particles of window pane near a hole are unable to share the fast motion of the bullet and so remain undisturbed.

Question 7.
China wares are wrapped in a straw paper before packing why?
Answer:
The straw paper between the china-wares increases the time of experiencing the jerk during transportation. Hence they strike against each other with less force and are less likely to get damaged.

Question 8.
Why it is necessary to bend knees while jumping from greater height?
Answer:
During the jump, our feet comes to rest at once and for this smaller time a larger force a acts on feet. If we bend the knees slowly, the value of time impact increases and less force acts on our feet. So we get less hurt.

Question 9.
Why is it difficult to drive a nail into a wooden block without supporting it?
Answer:
When we hit the nail with the hammer the nail and unsupported block together move forward as a single system. There is no force of reaction. When the block is rested against support, the reaction of the support holds the 14. block in position and nail is driven into the block.

Question 10.
Why is static friction called a self-adjusting force?
Answer:
As applied force increases, the static friction also increases and becomes equal to the applied force. That is why static friction is called a self-adjusting force.

Question 11.
Carts with rubber tyres are easier to fly than those with iron wheels. Why?
Answer:
The coefficient of friction between rubber tyres and road is much smaller than that between iron wheels and road.

Question 12.
Why ball bearings are used in machinery?
Answer:
By using ball bearings between the moving parts of the machinery the sliding friction gets converted into rolling friction. The rolling friction is much lesser than the sliding friction. This reduces power dissipation.

Question 13.
A bird is sitting on the floor of a closed glass cage and the cage is in the hand of a girl. Will the girl experience any change in weight of the cage when the bird –
(i) starts flying in the cage with a constant velocity
(ii) flies upwards with acceleration
(iii) fies downwards with acceleration.
Solution:
In a closed cage, the inside air is bound with a cage.
(i) As the acceleration is zero, there is no change in the weight of the cage.
(ii) while flying upwards R – Mg = Ma
R = M (a+g)
The cage will appear heavier

(iii) while flying downwards
Mg – R – Ma
R = M (g – a)
The cage will appear lighter.

Question 14.
A long rope is hanging, passing over a pulley. Two monkeys of equal weight climb up from the opposite ends of the rope. One of them climbs up more rapidly relative to rope. Which monkey will reach the top first? Pulley is frictionless and the rope is mass less and inextensible.
Answer:
There is no external force which may provide momentum to any monkey. The monkeys themselves give equal momenta to each other. Therefore two monkeys will climb up the rope at the same rate relative to earth. As their masses are equal they will reach the top simultaneously.

Question 15.
A light string passing over a smooth pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8. Find the ratio of the two masses.
Answer:

Question 16.
Briefly explains how a horse is able to pull a cart?
Answer:

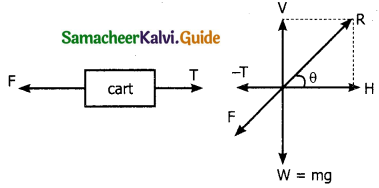
Consider a cart connected to a horse by a string. The horse while pulling the cart produces a Tension T in the string in their forward direction (action). The cart in turn pulls the horse by an equal force T in opposite direction.

Initially, the horse presses the ground with a force ‘F’ in an inclined direction. The reaction ‘R’ of the ground acts on the horse in the opposite direction.

The reaction ‘R’ can be resolved into two perpendicular components.
1) The vertical components ‘V balances the weight of the horse.
2) The horizontal components ‘H’ helps the horse to move forward.
Let F be the force of friction.
The horse moves forward if H > T.
In that case net force acting on horse = H – T
If m is mass of horse and ‘a’ be its acceleration.
H – T = ma → (1)
The cart moves forward if T > F.
In this case, net force acting on the cart = T – F.
The weight of the cart is balanced by the reaction of the ground acting on it.
If M is the man of cart and a is its acceleration T-F = Ma -»(2).
Adding (1) & (2)
H – F = (M+m)a
a = \(\frac { H-F }{ M+m }\)
obviously a is positive of H-F is positive or H > F. Thus the system moves.

Question 17.
A man of mass m is standing on the floor of a lift. Find his apparent weight when the lift is (i) moving upwards with uniform acceleration ‘a’ (ii) moving downwards with uniform acceleration a (iii) at rest or moving with uniform velocity (v) (iv) falling freely. Take acceleration due to gravity as g.
Answer:
Consider a man of mass ‘m’ standing on a weighing machine placed in a lift. The actual weight of the man is mg. It acts vertically downwards through center of gravity ‘G’ of the man, which acts in a weighting machine which offers a normal reaction ‘R’ read by a machine.
So R is the apparent weight of the man.

Case 1:
When the lift moves upwards with an acceleration ‘a’
The net upward force on the man = R – mg = ma
Apparent weight R = m(g+a)
So when the lift accelerates upwards, the apparent weight of man increases

Case 2:
When lift moves downwards with acceleration ‘a’ Net downward force: mg – R = ma R = m(g – a)
So when lift accelerates down, the apparent weight of man decreases.

Case 3:
When lifting at rest or moving with uniform velocity.
So acceleration ‘a’ = 0
Net force on man is R – mg = mx 0
R – mg = 0
R = mg
Apparent weight = actual weight

(iv) when lift falls freely a = g
the net downward force mg – R = ma
mg – R = mg
R = 0
The apparent weight of the man equal to zero.
Hence the person develops a feeling of weightlessness when he falls freely under gravity.

Question 18.
Derive the law of conservation of linear momentum from Newton’s third law of motion.
Answer:
Consider two bodies A and B of masses m₁ and m₂ moving in the same directions along the same line with velocities u₁ and u₂ respectively (U₁>u₂).
They collide for a time At. After the collision, their velocities be v₁ and v₂

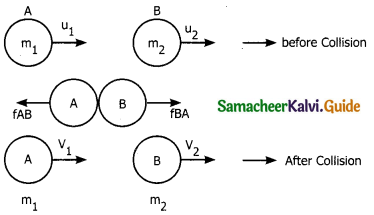
During collision the body A exerts a force F^BA on B and the body B exerts a force F^AB on A such that
F^BA = – F^AB
Impulse of F^AB = \(\overline{F}\)_AB ∆t = change in momentum is A
\(\overline{F}\)_BA ∆t = m₁\(\overline{v}\)₁ – m₁\(\overline{u}\)₁
Impulse of F_BA = \(\overline{F}\)_BA ∆t = change in momentum

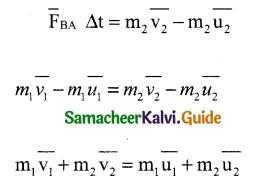
Total linear momentum after collision = Total linear momentum before collision
This proves the law of conservation of linear momentum.