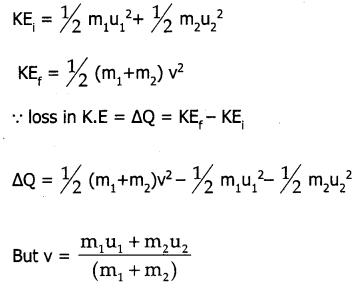Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Physics Guide Pdf Chapter 4 Work, Energy and Power Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 4 Work, Energy and Power
11th Physics Guide Work, Energy and Power Book Back Questions and Answers
![]()
Part – I:
I. Multiple choice questions:
Question 1.
A uniform force of (2\(\hat{i}\) + \(\hat{j}\)) N acts on a particle of mass 1 kg. The particle displaces from position (3\(\hat{j}\) + \(\hat{k}\) )m to (5\(\hat{i}\) + 3\(\hat{j}\)) m. The work done by the force on the particle is _______. (AIPMT Model 2013)
a) 9 J
b) 6 J
c) 10 J
d) 12 J
Answer:
c) 10 J
Question 2.
A ball of mass 1 kg and another of mass 2 kg are dropped from a tall building whose height is 80 m. After, a fall of 40 m each towards Earth, their respective kinetic energies will be in the ratio of _______. (AIPMT model 2004)
a) \(\sqrt{2}\) : 1
b) 1 : \(\sqrt{2}\)
c) 2 : 1
d) 1 : 2
Answer:
d) 1 : 2
Question 3.
A body of mass 1 kg is thrown upwards with a velocity 20 m s-1. It momentarily comes to rest after attaining a height of 18 m. How much energy is lost due to air friction? (Take g= 10ms-2 ) (AIPMT 2009)
a) 20 J
b) 30 J
c) 40 J
d) 10 J
Answer:
a) 20 J
![]()
Question 4.
An engine pumps water continuously through a hose. Water leaves the hose with a velocity v and m is the mass per unit length of the water of the jet. What is the rate at which kinetic energy is imparted to water? (AIPMT 2009)
a) \(\frac { 1 }{ 2 }\) mv3
b) mv3
c) \(\frac { 3 }{ 2 }\)mv²
d) \(\frac { 5 }{ 2 }\) mv²
Answer:
a) \(\frac { 1 }{ 2 }\) mv3
Question 5.
A body of mass 4 m is lying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each of mass m move perpendicular to each other with equal speed v. The total kinetic energy generated due to explosion is _______. (AIPMT 2014)
a) mv²
b) \(\frac { 3 }{ 2 }\)mv²
c) 2 mv²
d) 4 mv²
Answer:
b) \(\frac { 3 }{ 2 }\)mv²
Question 6.
The potential energy of a system increases, if work is done _______.
a) by the system against a conservative force
b) by the system against a non-conservative force
c) upon the system by a conservative force
d) upon the system by a non-conservative force
Answer:
a) by the system against a conservative force
Question 7.
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
a) \(\sqrt{2gR}\)
b) \(\sqrt{3gR}\)
c) \(\sqrt{5gR}\)
d) \(\sqrt{gR}\)
Answer:
c) \(\sqrt{5gR}\)
![]()
Question 8.
The work done by the conservative force for a closed path is _______.
a) always negative
b) zero
c) always positive
d) not defined
Answer:
b) zero
Question 9.
If the linear momentum of the object is increased by 0.1%, then the kinetic energy is increased by _______.
a) 0.1 %
b) 0.2%
c) 0.4%
d) 0.01%
Answer:
b) 0.2%
Question 10.
If the potential energy of the particle is α – \(\frac { β }{ 2 }\)x², then force experienced by the particle is _______.
a) F = \(\frac { β }{ 2 }\)x²
b) F = βx
c) F = – βx
d) F = – \(\frac { β }{ 2 }\)x²
Answer:
c) F = – βx
Question 11.
A wind-powered generator converts wind energy into electric energy. Assume that the generator converts a fixed fraction of the wind energy intercepted by its blades into electrical energy. For wind speed v, the electrical power output will be proportional to
a) v
b) v²
c) v3
d) v4
Answer:
c) v3
![]()
Question 12.
Two equal masses m1 and m2 are moving along the same straight line with velocities 5ms-1 and -9ms-1 respectively. If the collision is elastic, then calculate the velocities after the collision of m1 and m2, respectively _______.
a) -4ms-1 and 10 ms-1
b) 10ms-1 and 0 ms-1
c) -9ms-1 and 5 ms-1
d) 5 ms-1 and 1 ms-1
Answer:
c) -9ms-1 and 5 ms-1
Question 13.
A particle is placed at the origin and a force F= kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) versus x will be (where U is the potential energy function) (IIT 2004)
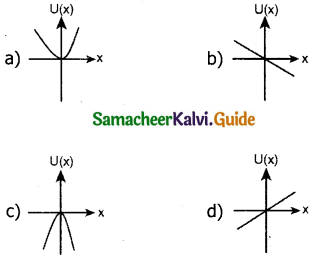
Answer:
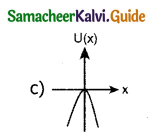
Question 14.
A particle which is constrained to move along x-axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x) = – kx + ax3. Here, k and a are positive constants. For x > 0, the functional form of the potential energy U(x) of the particle is _______. (IIT 2002)
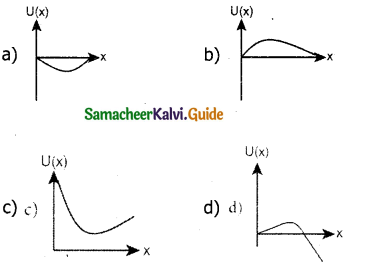
Answer:
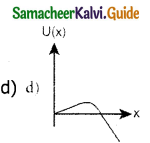
Question 15.
A spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then, the long piece will have a force constant of _______.
a) \(\frac { 2 }{ 3 }\) k
b) \(\frac { 3 }{ 2 }\) k
c) 3k
d) 6k
Answer:
b) \(\frac { 3 }{ 2 }\) k
![]()
II. Short Answer Questions:
Question 1.
Explain how the definition of work in physics is different from general perception.
Answer:
The term work is used in diverse contexts in daily life. It refers to both physical as well as mental work. In fact, any activity can generally be called work. But in Physics, the term work is treated as a physical quantity with a precise definition. Work is said to be done by the force when the force applied to a body displaces it.
Question 2.
Write the various types of potential energy. Explain the formulate.
Answer:
The energy possessed by the body by virtue of its position is called potential energy.
The various types of potential energies are
1) Gravitational potential energy :
The energy possessed by the body due gravitational force gives gravitational potential energy
u = mgh.
where
u → Gravitational potential energy
m → Mass of the body
g → acceleration due to gravity
h → displacement produced
2) Elastic potential energy :
The energy due to spring force and other similar forces give rise to elastic potential energy
u = 1/2² Where
U → elastic potential energy
K → spring constant
x → elongation produced
3) Electrostatic potential energy
The energy due to electro static force on charges give rise to electrostatic potential energy
U = K \(\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}}\) where
K = \(\frac{1}{4 \pi \varepsilon_{0}}\) Constant
q1, q2 – magnitude of charges
d – displacement made by any one of the charges or by both charges.
![]()
Question 3.
Write the differences between conservative and non-conservative forces. Give two examples each.
Answer:
Conservative forces:
A Force is said to be a conservative force if work done by or against the force in moving the body depends only on the initial and final positions of the body and net depend on the nature of the path followed between the two positions
Examples:
Elastic spring force, electrostatic force, magnetic force, gravitational force.
Non-conservative force:
A force is said to be non-conservative if the work done by or against the force in moving a body depends on the path between initial and final positions. This means the value of work-done is different in different paths.
Examples:
- Frictional forces are non-conservative forces as the work done against friction depends on the length of the path moved by the body.
- The force due to air resistance, viscous forces are also non conservative forces because work done by or against these forces depends upon the velocity of motion.
Question 4.
Explain the characteristics of elastic and inelastic collision Elastic collision:
Answer:
In a collision, the total K.E of the bodies before collision is equal to the total K.E. of the bodies after collision, then it is an elastic collision.
Total K.E. before collision = Total K.E. after collision
Inelastic collision:
In a collision, the total K.E. of the bodies before collision is not equal to total K.E. after collision then it is called as inelastic collision Even though K.E. is not conserved but total energy is conserved. After collision of the two colliding bodies stick together such collision are called as perfectly inelastic a plastic collision.
![]()
Question 5.
Define the following
Answer:
a) Coefficient of restitution
b) Power
c) Law of conservation of energy
d) Loss of Kinetic energy in inelastic collision
Answer:
a) Coefficient of restitution :
Coefficient of restitution defined as the ratio of velocity of separation (after collision) to velocity of approach (before collision)
The coefficient of restitution = 
b) Power :
Power is defined as the rate of work done or energy delivered
P = \(\frac { W }{ t }\) = \(\vec{F}\).\(\vec{V}\)
c) Law of conservation of energy :
Law states that “Energy can neither be created nor destroyed. It may be transformed from one to another but the total energy of an isolated system remains constant”
d) Loss of kinetic energy in inelastic collision
The difference in total K.E. before collision and total K.E. after collision’s is equal to loss of K.E. during collision.
∆Q = Total K.E. before collision – Total K.E. after collision.
![]()
III. Long Answer Questions:
Question 1.
Explain with graphs the difference between work done by a constant force and by a variable force.
Answer:
a) Work done by a constant force:
When a constant force ‘F’ acts on a body the small work done (dw) by the force in producing a small displacement ‘dr’ is given by dw = (F cos θ) dr.
The total W.D in producing a displacement from initial position ri, to final position rf is,
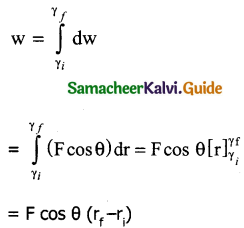
The graphical representation of the W.D by constant force is shown below
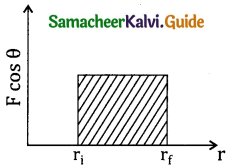
The area under the graph shows the work done by constant force.
b) Work done by a variable force :
When the component of a variable force F acts on a body, the small work done (dw) by the force in producing a small displacement dr is given by dw = (F cos θ) dr [ Here F cos 0 is the component of variable forces]. where F and 0 one variables To total W.D for the displacement from initial position ri to final position rf is given by the relation.
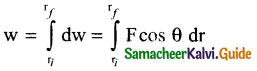
A graphical representation of the work done by a variable force is shown below. The area under the graph gives the W.D. by variable force.
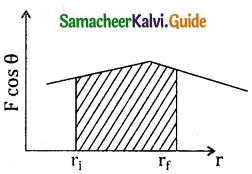
Question 2.
State and explain work energy principle Mention any three examples for it.
Answer:
Law:
Work done by a force on the body changes the kinetic energy of the body, ie change in K.E. = work done. This is called work energy theorem.
Proof:
Consider a body of mass m at rest on a frictionless horizontal surface. The work done (W) done by the constant force (F) for displacement (S) in the same direction is W = FS → (1)
The constant force is given by F = ma → (2)
We know that v² = u² + 2a

W = 1/2 mv² – 1/2 mu²
Here the term 1/2 mv² indicates K.E.
1/2 mv² – 1/2mu² = ∆K (change in K.E.)
∵ W = ∆K
Hence proved
Examples:
- A moving hammer drives a nail into the wood. Being in motion, it has K.E. or ability to do work.
- A fast moving stone can break a windowpane. The stone has K.E. due to its motion and so it can do work.
- The kinetic energy of air is used to run windmills.
![]()
Question 3.
Arrive at an expression for power and velocity. Give some examples for the same.
Answer:
Power is defined as the rate of work done or energy delivered. P = \(\frac { w }{ t }\)
Relation between power and velocity:
The work done by a force F for a displacement \(\overline{dr}\) is dw = \(\overline{F}\).\(\overline{dr}\)

Examples:
1) A 100 Watt bulb consumes 100 joule of electrical energy in one second
2) Electrical motor supply enough power to bring water from a bore well.
Question 4.
Arrive at an expression for elastic collision in one dimension and discuss various cases.
Answer:
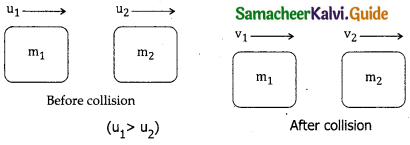
Consider two elastic bodies of masses m1 and m2 moving in a straight line (along positive direction) on a frictionless horizontal surface. In order to have collision assume m1 moves faster than m2.
Let U1 and 1 be the initial velocities of m1 and m2 respectively. (u1 > u2). After collision let the masses m1 and m2 moves with velocities v1 and v2 respectively.
Incase of elastic collision both linear momentum and kinetic energies are conserved
∴ from law of conservation of linear momentum
Total momentum before (Pi)
collision = Total momentum afer collision (Pf)
m1u1 + m2u2 = m1v1 + m2v2 → (1)
m1(u1 – v1) = m2(v2 – u2 → (2)
Further
Total K.E. before collision (KEi) = Total K.E. after collision (KEf)

rearranging
u1 – u2 = – (v1 – v2) → (5)
From this it is dear that for any elastic collision, relative speed of two elastic bodies after the collision has the same magnitude as before collision but in opposite direction.
Rewriting the above equation for v1 & v1
v1 = v2 + u2 – u1 → (6)
(or)
v2 = v1 + u1 – u2 → (7)
To find velocities of v1 & v2
Substituting (7) in (2)
m1(u1 – v1) = m2(v1 + u1 – u2 – u2)
m1(u1 – v1) = m2(v1 + u1 – 2u2)
m1u1 – m1v1 = m2v1 + m2u1 – 2m2u2
m1u1 – m2u1 + 2m2u2 = m1v1 + m2v1
u1(m1 – m2) + 2m2u2 = v1(m1 + m2)

Case 1:
When bodies have same mass is m1 = m2 = m
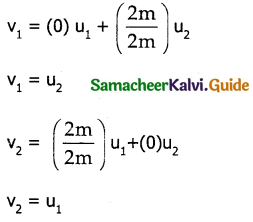
The velocities get interchanged.
Case 2:
When both bodies have same mass m1 = m2 = m, but second body at rest in u2 = 0
v1 = 0, v2 = u1
After collision the first body comes to rest and the second body moves with the velocity of first body.
Case 3 :
The first body very much lighter than the second body in m1 << m2, \(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}\) << 1.
the ratio \(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}\) = 0 and also second body at rest, (u2 = 0)
Dividing numerator and denominator of equation 8 by m2
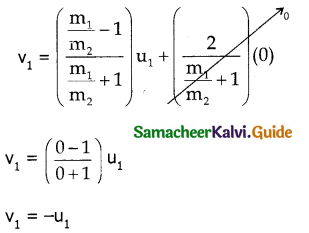
Similarly dividing numerator and denominator of equation 9 by m1
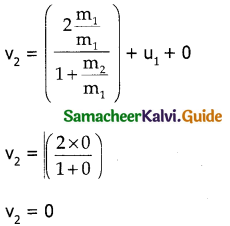
From this, the conclusion arrived is the first body which is lighter returns back (rebounds) in opposite direction with the same initial velocity as it has a negative sign. The second body since it has heavier mars continues to remain at rest even after the collision.
Case 4 :
The second body is very much lighter than the first body.
m2 << m1 then the ratio = 0 \(\frac{\mathrm{m}_{2}}{\mathrm{~m}_{1}}\) and also if the target is at rest ie second body at rest (u2 = 0)
Dividing equation (8) both the numerator and denominator by m1

This shows that the first body which is heavier continues to move with same velocity and the second body which is lighter will move with twice the initial velocity of the first body, ie lighter body is thrown away from the point of collision.
Question 5.
What is inelastic collision? In which way it is different from elastic collision mention few examples in day to day life for inelastic collision.
Answer:
In a collision, the total K.E. on the bodies before collision is not equal to the total K.E. after collision then it is called as inelastic collision, i.e
Total K.E after collision ≠ Total K.E. before collision
Whereas in case of elastic collision Total K.E. before collison is equal to total K.E after collision.
Example: Collision between two vehicles, collision between a ball and floor.
![]()
IV. Numerical Problems:
Question 1.
Calculate the work done by a force of 30N in lifting a load of 2kg to a height of 10m (g = 10ms-2)
Solution:
F = 30N
m = 2kg
s = 10 m
g = 10 ms-2
θ = 0
W.D = ?
W.D = \(\overline{F}\).\(\overline{S}\) = FS cos θ
W.D = 30 x 10
= 300 J
Question 2.
A ball with a velocity of 5 ms-1 impinges at an angle of 60° with the vertical on a smooth Horizontal plane. If the coefficient of restitution is 0.5 find the velocity and direction after the impact.
Solution:
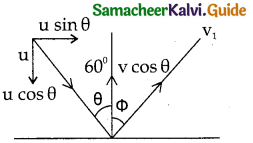
U1 = 5 ms-1
θ = 60°
e = 0.5
v = ?
Initial momentum = final momentum along the original line of m of con.
∵ Coefficient of restitution is 0.5 (less than 1) the collision is inelastic
Applying component of velocities. The x component of velocity is
u sin θ = v sin Φ → (1)
But the magnitude of y component is not same using coefficient of restitution
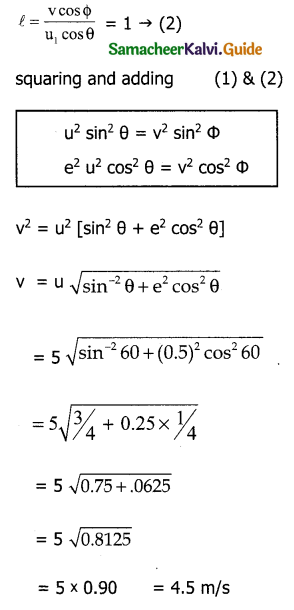
Question 3.
A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure. What initial speed must be given to the object to reach the top of the circle?. (Hint: use law of conservation of energy). Is this speed less or greater than speed obtained in the section 4.2.9?
Solution:
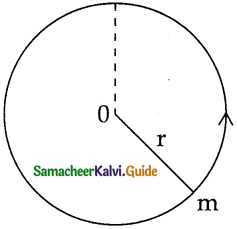
T.E. at lowest point (E1) = Total energy at (E2)
E1 = E2
At the lowest point potential energy = u1 = 0
Kinetic energy = KE1 = 1/2 mv1²
Total energy at lowest point = E1 = u1 + KE1
E1 = 0 + 1/2 mv² → (1)
∴ E1 = mv²1 … (1)
At the top of circle:
Potential energy = u2 = 2mgr
K.E energy at top = 1/2mv2²
Total energy at highest
point = 2mgr + 1/2 mv2² → (2)
According to law of conservation of energy E1 = E2

Question 4.
Two different unknown masses A and B collide. A is initially at rest when B has a speed V. After collision B has a speed V/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.
Solution:
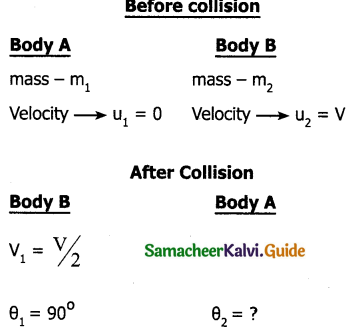
Applying principle of conservation of momentum along x-axis
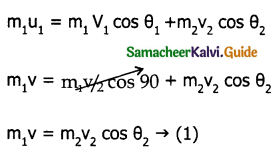
Applying principle of conservation of momentum along y-axis
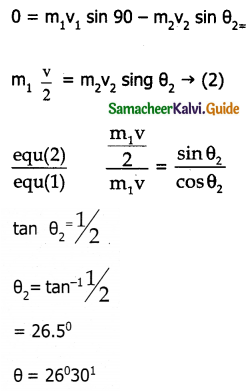
Question 5.
A bullet of mass 20g strikes a pendulum of mass 5 kg. The centre of mass of the pendulum rises at a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.
Solution:
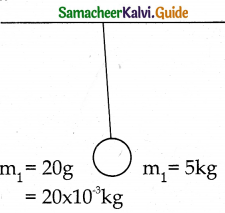
mass of bullet m1 = 20 x 10-3kg
mass of pendulum m2 = 5kg
Let the speed of the bullet = u1
∵ The pendulum at rest u2 = 0
h = 10 x 10-2m
Let v be the common velocity after the bullet embedded inside the bob.
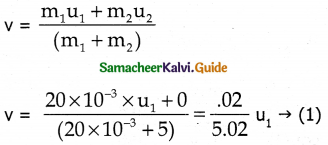
This common velocity ‘v’ is the initial velocity of combined bullet and bob.
W.K.T
v² – u² = 2as
Here v = 6; u = 0, a = – g s = h

V. Conceptual Questions:
Question 1.
A spring which is initially in the unstretched condition is first stretched by a length x and again by a further length x. The work done in the first case w1 is one-third of the work done in the second case w2. True or false?
Answer:
True, W.D by the first case will be 1/3 of the second W.D

Question 2.
Which is conserved in inelastic collision? Total energy (or) kinetic energy?
Answer:
In inelastic collision total energy is only conserved but kinetic energy is not conserved. A part of kinetic energy is converted into some other form of energy such as sound, heat energy.
Note: The linear momentum is also conserved.
Question 3.
Is there any network done by external forces on a car moving at a constant speed along a straight road?
Answer:
Since the car is moving at a constant speed along a straight line, displacement is caused. So work in done by the force.
![]()
Question 4.
A car starts from rest and moves on a surface with uniform acceleration. Draw the graph of kinetic energy versus displacement. What information you can get from that graph?
Answer:
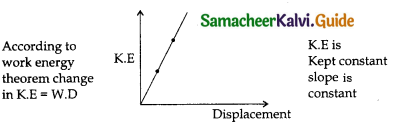
According to work-energy theorem change in K.E = W.D
K.E is Kept constant slope is constant
Question 5.
A charged particle moves towards another charged particle under what conditions the total momentum and the total energy of the system conserved?
Answer:
Coulomb force is acting in between the charged particles Internal force is a conservative force. If no external forces act or the work done by external forces is zero then the mechanical energy of the system and also total linear momentum also remains constant.
![]()
11th Physics Guide Work, Energy and Power Additional Important Questions and Answers
I. Multiple choice questions:
Question 1.
Thrust and linear momentum
(a) Thrust and linear momentum
(b) Work and energy
(c) Work and power
(d) Power and energy
Answer:
(b) Work and energy
Question 2.
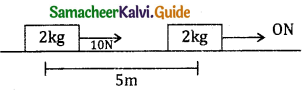 For the surface μ = 0.4, The work done by applied force, frictional force and net force are
For the surface μ = 0.4, The work done by applied force, frictional force and net force are
a) 50J, -40J, 10J
b) 50J, -20J, 10J
c) 10J, -50J, 40J
d) 50J, -40J, 20J
Answer:
a) 50J, -40J, 10J
Question 3.
The system is released from rest. Find the work done by the force if gravity during first 2 seconds of motion.
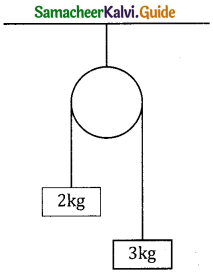
a) 80J
b) 20J
c) 40J
d) 100J
Answer:
c) 40J
![]()
Question 4.
Dimensional formula for work done is
(a) MLT-1
(b) ML2T2
(c) M-1L-1T2
(d) ML2T-2
Answer:
(d) ML2T-2
Question 5.
The variation of force acting on a particle along x ax is is shown. The W.D by the force during the displacement x = 0 to x = 25m is _______.
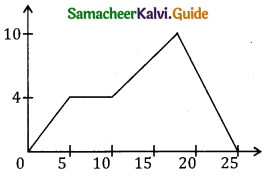
a) 100J
b) 115J
c) 130J
d) 125J
Answer:
b) 115J
Question 6.
The amount of work done by centripetal force on the object moving in a circular path is
(a) zero
(b) infinity
(c) positive
(d) negative
Answer:
(a) zero
Question 7.
A ball of mass 200g is attached to a string 50 mm and a force F is applied as shown. The W.D by this force if the string makes an angle 60° with vertical is? [at initial and final positions speed of the ball is zero.]
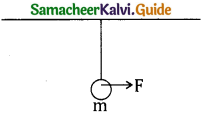
a) 1J
b) 0.5J
c) 0.05J
d) 0.25J
Answer:
b) 0.5J
Question 8.
An object of mass 4kg falls from rest through a vertical distance of 20m and reaches with velocity 10ms-1 on ground. The work done by air friction is .
a) 800J
b) – 800J
c) 600J
d) – 600J
Answer:
d) – 600J
Question 9.
If the force and displacement are perpendicular to each other, then the work done is
(a) positive
(b) negative
(c) zero
(d) maximum
Answer:
(c) zero
Question 10.
What is the power of an engine which can lift 600kg of coal per minute from a mine 20m deep?
a) 2000 w
b) 100 w
c) 1000 w
d) 200 w
Answer:
a) 2000 w
Question 11.
If w1, w2 and w3 represent the work done in moving a particle from A to B along 3 different paths 1, 2 and 3 respectively as shown in figure, in the gravitational field of a point mass m. Find the correct relation an between w1, w2 and w3 _______.
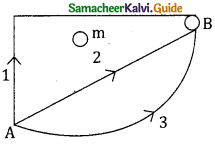
a) w1 > w2 > w3
b) w1 = w2 = w3
c) w1 < w2 < w3
d) w2 > w1 > w3
Answer:
b) w1 = w2 = w3
![]()
Question 12.
A position – depends force F = 7 – 2x + 3x² newton acts on a small body of mass 2kg and displacement if from x = 0 to x = 5m. The work done in Joule is _______.
a) 70
b) 270
c) 35
d) 135
Answer:
d) 135
Question 13.
The energy possessed by a body due to its motion is called as
(a) potential energy
(b) kinetic energy
(c) mechanical energy
(d) none
Answer:
(b) kinetic energy
Question 14.
According to the work-energy theorem, the work done by the net force on a particle is equal to change in its _______.
a) kinetic energy
b) potential energy
c) linear momentum
d) angular momentum
Answer:
a) kinetic energy
Question 15.
A block of 2kg is resting on a smooth surface. At what angle a force of 10N be acting on the block so that it will acquire a K.E of 10J after moving 2m _______.
a) 30°
b) 60°
c) 45°
d) 90°
Answer:
b) 60°
Question 16.
The K.E acquired by a body of mass m in travelling a certain distance starting from rest under a constant force is _______.
a) directly proportional to m
b) directly proportional to \(\sqrt{m}\)
c) inversely proportional to \(\sqrt{m}\)
d) independent of m
Answer:
b) directly proportional to \(\sqrt{m}\)
Question 17.
1-kilowatt hour is equivalent to
(a) 10-7 J
(b) 1.6 × 10-19 J
(c) 4.186 J
(d) 3.6 × 10-6 J
Answer:
(d) 3.6 × 10-6 J
![]()
Question 18.
A particle moves in a straight line with retardation proportional to displacement. Its loss of K.E in any displacement x is proportional to _______.
a) x²
b) ex
c) x
d) logex
Answer:
a) x²
Question 19.
Which one of the following is not a conservative force?
a) gravitational force
b) electrostatic force between the charges
c) Magnetic force between two magnetic dipoles
d) Frictional force
Answer:
d) Frictional force
Question 20.
A spring of force constant 800 N/M has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is _______.
a) 163
b) 8J
c) 32J
d) 24J
Answer:
b) 8J
Question 21.
The kinetic energy of the body is always
(a) zero
(b) infinity
(c) negative
(d) positive
Answer:
(d) positive
Question 22.
A bullet moving with a speed of 150 m/s strikes a wooden plank. After passing through the plank its speed becomes 125ms-1. Another bullet of the same mass and size strikes the plank with a speed of 90m/s. Its speed after passing through the plank would be _______.
a) 25 m/s
b) 35 m/s
c) 50 m/s
d) 70 m/s
Answer:
a) 25 m/s
Question 23.
A 2kg block slides on a horizontal floor with a speed of 4 m/s. It strikes on uncompressed spring and compresses it fill the block is motionless. The kinetic friction force is 15N and spring constant is 104N/m. The spring compress by _______.
a) 5.5 cm
b) 2.5 cm
c) 11 cm
d) 8.5 cm
Answer:
a) 5.5 cm
![]()
Question 24.
If two objects of masses m1 and m2 (m1 > m2) are moving with the same momentum then the kinetic energy will be greater for
(a) m1
(b) m2
(c) m1 or m2
(d) both will have equal kinetic energy
Answer:
(b) m2
Question 25.
The power of a pump which can pump 200 kg of water to a height if 200m in 10s is _______. (g = 10ms-2)
a) 40 kW
b) 80 Kw
c) 400 Kw
d) 960 Kw
Answer:
a) 40 Kw
Question 26.
A body of mass m accelerates uniformly from rest to velocity v0 in a time t0. The instantaneous power delivered to the body at any time t is _______.
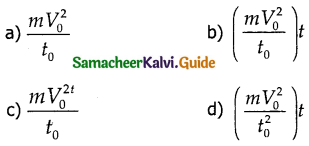
Answer:
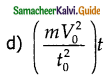
Question 27.
particle to mass ‘m’ starting from rest undergoes uniform acceleration. If the speed acquired in time T is V, the power delivered to the particle is _______.
a) \(\frac{M V^{2}}{T}\)
b)\(\frac { 1 }{ 2 }\)\(\frac{M V^{2}}{T^{2}}\)
c) \(\frac{M V^{2}}{T^{2}}\)
d) \(\frac { 1 }{ 2 }\)\(\frac{M V^{2}}{T}\)
Answer:
d) \(\frac { 1 }{ 2 }\)\(\frac{M V^{2}}{T}\)
Question 28.
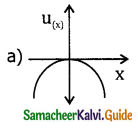
A particle is placed at the origin and a force F = kx is acting on it (where k is the positive constant). If U (o) = 0, the graph u(x) verses x will be _______. (u=potential energy function)
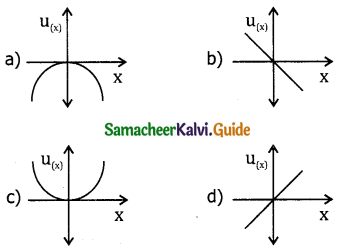
Answer:
Question 29.
The force acting on a body moving along x-axis varies with the position of the particle as in fig _______.
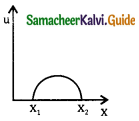
The body in stable equilibrium at
a) x = x1
b) x = x2
c) both x1, and x2
d) neither x1 nor x2
Answer:
b) x = x2
Question 30.
Non-conservative force is
(a) frictional force
(b) viscous force
(c) air resistance
(d) all the above
Answer:
(d) all the above
![]()
Question 31.
If the K.E of the body is increased by 300% then for the percentage change in momentum will be _______.
a) 100%
b) 150%
c) 265%
d) 73.2%
Answer:
a) 100%
Question 32.
A particle is projected making an angle 45’ with horizontal having kinetic energy k. The K.E at the highest point will be _______.
a) K/\(\sqrt{2}\)
b) K/2
c) 2K
d) K
Answer:
b) K/2
Question 33.
The coefficient of restitution e for a perfectly elastic collision is _______.
a) 1
b) 0
c) ∞
d) -1
Answer:
a) 1
Question 34.
A ball moving with a certain velocity hits another identical ball at rest. If the plane is frictionless and collision is elastic, the angle between the directions in which the balls move after collision will be _______.
a) 30°
b) 60°
c) 90°
d) 120°
Answer:
c) 90°
Question 35.
Which of the following is zero at the highest point in vertical circular motion?
(a) velocity of the particle
(b) tension of the spring
(c) potential energy
(d) none
Answer:
(a) velocity of the particle
![]()
II. Additional Questions:
Question 1.
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative.
(a) Work done by man lifting a bucket out of the well by means of a rope tied to the bucket
Solution:
Work done is positive, because the bucket moves in the direction of force applied by the man.
(b) work done by gravitational of force in the above case.
Solution:
work done by gravitational force in negative because the bucket is moving upwards against gravitational force.
(c) Work done by friction on a body sliding down an inclined plane.
Solution:
Work done is negative, as frictional force is opposite to direction of motion.
(d) work done by the applied force on a body moving on a rough horizontal plane with uniform velocity.
Solution:
Work done is positive because the applied force acts in the direction of motion of the body
(e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Solution:
Work done is negative, because the resistive force of air acts in a direction opposite to the direction of motion of the vibration pendulum.
Question 2.
Comets move around the sun in highly elliptical orbits. The gravitational force an the comet due to sun is not normal to the comet velocity in general. Yet the W.D by the gravitational force over every complete orbit of the comet is zero why?
Solution:
The gravitational force acting on the comet is a conservative force. The work done by the conservative force over any path is equal to the negative of change in potention energy. Over a complete orbit of any shape, there is no change in P.E of the comet. Hence no work is done by the gravitational force on the comet.
![]()
Question 3.
A body is moving unidirectionally under the influence of a source of constant power. How displacement (S) and time (t) are related?
Answer:
By work energy theorem
W = Pxt = 1/2 mv²
v² = \(\frac { 2pt }{ m }\)

Question 4.
A molecule in a gas container hits a horizontal wall with speed 200 ms-1 and angle 30° with normal and rebounds with same speed. Is momentum conserved in collision? Is the conserved is elastic or in elastic.
Solution:
Momentum is always conserved, whether collision is elastic or in elastic
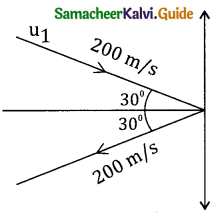
Let m be the mars of the molecule and M be the mass of the wall. As the wall is heavy the molecule rebounding with same velocity does not produce any velocity to wall.
K.E. before collision = Ki = 1/2 m(200)² + 0
= 2 x 104 x 1/2m – 3
K.E. after collision = Kf = 1/2 m(200)² + 0
= 1/2 x m x 2 x w4
∵ Ki = Kf
Collision is elastic in nature
Question 5.
An elastic spring of force constant K is compressed by a amount x. Show that its potential energy is 1/2 kx².
Answer:
Consider the plot of spring force Fs versus displacement x of the block attached to free end of a spring.
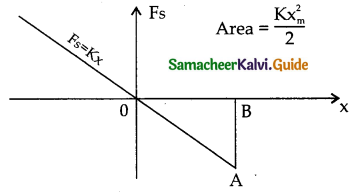
According to Hookes law Fs = – k xm
The work done by the spring force for an extension xm is
Ws = Area ∆OBA = 1/2 AB x OB
= 1/2 Fs Xm
= 1/2 (-kxm) xm²
Ws = – 1/2 kxm²
In order stretch the spring slowly an external force F equal to and opposite to Fs has to be applied. So work done by the external force F is
W = – Ws = + 1/2 kxm²
This work done is stored as P.E of the spring
u = 1/2 kx²
Question 6.
Obtain the relation between momentum and K.E
Answer:
Consider an object of mass on moving with velocity v. Then its linear momentum is \(\overline{p}\) = \(\overline{mv}\) and its kinetic energy
k.E = 1/2 mv²
multiply and divide by m both numerator and denominator
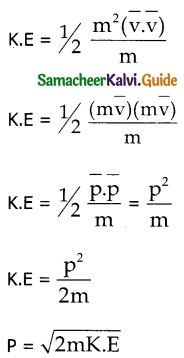
Question 7.
Explain motion of a body in vertical circle.
Answer:
Consider a body of mass m attached to one end of marsless and inextensible string executes circular motion is a vertical plane with other end fixed at 0. The length of the string equal to radius.
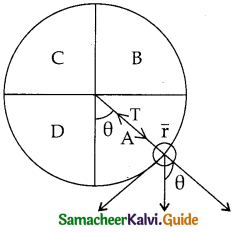
There are two forces acting an mass m.
i) Gravitational force (mg) which acts downwards
ii) Tension along the string (T)
Applying Newtons II law
mg sin θ = m at
mg sin θ = – m\(\frac { dv }{ dt }\) → (1)
Where at = tangential acceleration
In the radial direction
T – mg cos θ = m ar
T – mg cos θ = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\)
Where ar = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = centripetal or radial acceleration from the above 2 equations four important facts to get understood are.
1) The mass is having tangential acceleration (g sin θ) for all values of 0 (expect θ =0°). It is clear that vertical circular motion is not a uniform circular motion
2) From (1) & (2) as the magnitude of velocity is not constant in the course of motion, the Tension in the string is also not constant.
3) From equ(2) T = mg cos θ + \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\), indicates that in section A and D (for – π/2 < θ < π/2) cosθ is five, ie the term mg cos θ is always > 0.
Hence Tension can not vanish even when the velocity vanishes.
4) The equation (2) \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = T – mg cos θ further indicates that in section B and C
(for π/2< θ < 3π/2) cosθ is negative.
(-mg con θ) is always greater than zero. Hence velocity cannot vanish even tension vanishes.
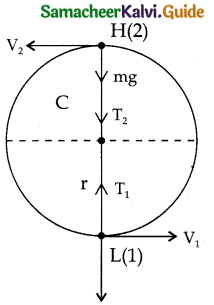
Consider two positions, lowest position (1) and the highest position 2.
Let v1 be the velocity at the lowest point 1.
Let v2 be the velocity at the lowest point 2.
The direction of velocity is always tangential to the circular path at all points.
Let T1 and T2 be the Tensions at lowest end highest point respectively. Tension at each point act towards the centre. Tension and Similarly velocity can be determined by applying the law of conservation of energy.
For the lowest point (1)
when the body is at its lowest point (1) the gravitational force mg which acts vertically downwards and Tension (T1) vertically upwards.
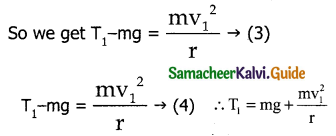
For the highest point:
At the highest point (2) both gravitational force mg and tension T2 act vertically downwards.

Here the term can (v1² – v2²) be found by applying law of conservation of energy at point 1 and 2.
Total energy at 1 = Total energy at 2
E1 = E2
P.E at 1, u1 = 0
K.E at 1, KE1 = 1/2 mv1²
T.E at 1 = 1/2 0 + mv1² = 1/2 mv1² → (8)
Similarly
P.E at 2, u2 = mg(2r)
K.E at 2, K.E2 = 1/2 mv²
T.E at 2 = mg(2r) + 1/2 mv22 → (9)
equating (8) and (9)
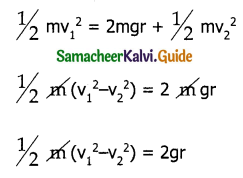
(v1² – v2²) = 4gr → (10)
Substituting (10) in (7)
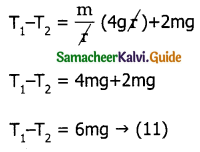
Minimum speed at the highest point (2)
In order to loop the circle, the body must have a minimum speed at point 2 – To find minimum speed at 2 consider 2.
Consider T2 = 0 in equation … (6)

At highest point 2 the body should have a minimum velocity v2 = \(\sqrt{gr}\) to stay in circular path.
Minimum speed at the lowest point:
From equation 10
v1² – v2² = 4gr
v1² – gr = 4gr
v1² = \(\sqrt{5gr}\)
The body must have a speed of \(\sqrt{5gr}\) at the lowest point 1.
ie v1 ≥ \(\sqrt{5gr}\) so that the mars can stay in circular path.
Comparing values of v1 & v2 it is clear that minimum speed at the lowest point should be \(\sqrt{5}\) times more than the minimum speed at the highest point, so that the body loops in a vertical circle.
![]()
Question 8.
What is perfect in elastic collision?
Answer:
Obtain an expression for velocity after collision. A perfect or complete in elastic collision is the are in which the object stick permanently after collision such that they move with a common velocity.
Expression for common velocity:
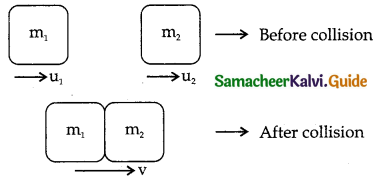
Let two bodies of masses m1 and m2 move with initial velocities u1 and u2 respectively before collision. After perfect inelastic collision both two objects move together with a common velocity v.
Since linear momentum is conserved during collisions.
m1u1 + m2u2 = (m1 + m2)v
V = \(\frac{\mathrm{m}_{1} \mathrm{u}_{1}+\mathrm{m}_{2} \mathrm{u}_{2}}{\left(\mathrm{~m}_{1}+\mathrm{m}_{2}\right)}\)
This gives the expression for common velocity.
Question 9.
Obtain an expression for loss of K.E. in perfect elastic collision.
Answer:
Let KEi be the initial total kinetic energy before collision and KEf be the total final kinetic energy after collision.