Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1
Question 1.
Find the rank of each of the following matrices
(i) \(\left(\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right)\)
Solution:
Let A = \(\left|\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right|\)
Order of A is 2 × 2 [∴ P(A) ≤ 2]
Consider the second order minor = \(\left|\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right|\)
= 40 – 42
|A| = -2 ≠ 0
There is a minor of order 2, which is not zero
ρ(A) = 2
![]()
(ii) \(\left(\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right)\)
Solution:
Let A = \(\left(\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right)\)
Order of A is 2 × 2 [∴ ρ(A) ≤ 2]
Consider the second order minor = \(\left|\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right|\)
= -6 – (-3)
= -6 + 3 = -3
|A| ≠ 0
There is a minor of order 2, which is not zero
∴ ρ(A) = 2
(iii) \(\left(\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right)\)
Solution:
Let A = \(\left(\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right)\)
Order of A is 2 × 2 [∴ ρ(A) ≤ 2]
Consider the second order minor = \(\left|\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right|\)
= 8 – 8 = 0
Since the second are minor vanishes, ρ(A) ≠ 2
Consider a first order minor |1| ≠ 0
There is a minor of order 1, which is not zero
∴ ρ(A) = 1
![]()
(iv) \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right]\)
Order of A is 3 × 3
∴ ρ(A) ≤ 2
Consider the third order minor \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right|\)
= 2(1 + 5) – (-1) (3 + 5) + 1 (3 – 1)
= 2 (6) + 1(8) + 1(2)
= 12 + 8 + 2
= 22 ≠ 0
There is a minor of order 3, which is not zero
∴ ρ(A) = 3
(v) \(\left[\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right]\)
Order of A is 3 × 3
∴ ρ(A) ≤ 3
Consider the third order minor \(\left|\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right|\)
= -1(12 – 16) – 2 (-16 + 8) – 2 (16 – 6)
= -1(-4) – 2 (-8) – 2 (10)
= 4 + 16 – 20
= 0
Since the third order minor vanishes, therefore
∴ ρ(A) ≠ 3
Consider a second order minor \(\left|\begin{array}{ll}
-1 & 2 \\
4 & -3
\end{array}\right|\)
= 3 – 8
= -5 ≠ 0
There is a minor of order 2, which is not zero.
∴ ρ(A) = 2
![]()

The order of A is 3 × 4
∴ ρ(A) ≤ 3
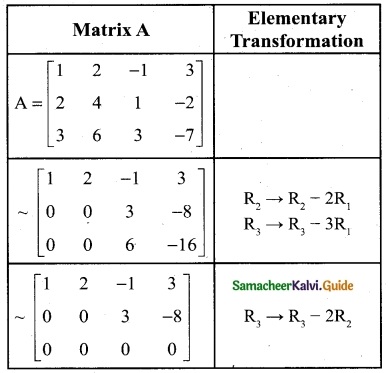
The number of non zero rows is 2
∴ ρ(A) = 2

The order of A is 3 × 4
∴ ρ(A) ≤ 3
Consider the third order minor \(\left|\begin{array}{ccc}
3 & 1 & -5 \\
1 & -2 & 1 \\
1 & 5 & -7
\end{array}\right|\)
= 3 (14 – 5) – 1 (- 7 – 1) – 5 (5 + 2)
= 3 (9) – 1 (-8) – 5 (7)
= 27 + 8 – 35
= 0
\(\left|\begin{array}{ccc}
1 & -5 & 1 \\
-2 & 1 & -5 \\
5 & -7 & 2
\end{array}\right|\)
= 1 (2 – 35) + 5 (-4 + 25) – 1 (14 – 5)
= 1 (-33) + 5(21) – 1 (9)
= -33 + 105 – 9
= 63 ≠ 0
There is a minor of order 3, which is not zero.
∴ ρ(A) = 3
![]()
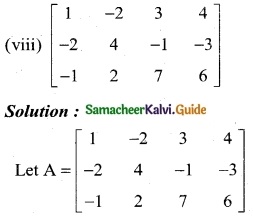
Order of A is 3 × 4
∴ ρ(A) ≤ 3
Consider the third order minor \(\left|\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -1 \\
-1 & 2 & 7
\end{array}\right|\)
= 1 (28 + 2)+ 2 (-14 – 1) + 3 (-4 + 4)
= 1 (30) + 2 (- 15) + 3 (0)
= 0
\(\left|\begin{array}{ccc}
-2 & 3 & 4 \\
4 & -1 & -3 \\
2 & 7 & 6
\end{array}\right|\)
= -2 (-6 + 21) – 3 (24 + 6) + 4 (28 + 2)
= -2(15) – 3 (30)+ 4 (30)
= 0
\(\left|\begin{array}{ccc}
1 & 3 & 4 \\
-2 & -1 & -3 \\
-1 & 7 & 6
\end{array}\right|\)
= 1 (-6 + 21) – 3 (-12 – 3) + 4 (-14 – 1)
= 1 (15) -3 (-15) + 4 (-15)
= 15 + 45 – 60
= 0
\(\left|\begin{array}{ccc}
1 & -2 & 4 \\
-2 & 4 & -3 \\
-1 & 2 & 6
\end{array}\right|\)
= 1 (24 + 6) + 2 (-12 – 3) + 4 (-4 + 4)
= 1 (30) + 2 (-15) + 4(0)
= 30 – 30
= 0
Since all third order minors vanishes, ρ(A) ≠ 3
Now, let us consider the second order minors.
Consider one of the second order minors
\(\left|\begin{array}{ll}
-2 & 3 \\
4 & -1
\end{array}\right|\) = 2 – 12 = -10 ≠ 0
There is a minor of order 2 which is not zero
∴ ρ(A) = 2
![]()
Question 2.
If A = \(\left(\begin{array}{ccc}
1 & 1 & -1 \\
2 & -3 & 4 \\
3 & -2 & 3
\end{array}\right)\) and B = \(\left(\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -6 \\
5 & 1 & -1
\end{array}\right)\)
find the rank of A B and the rank of B A.
Solution:

To find the rank of AB
Order of AB is 3 × 3
∴ ρ(AB) ≤ 3
Consider the third order minor |AB| = \(\left|\begin{array}{ccc}
-6 & 3 & -2 \\
28 & -12 & 20 \\
22 & -11 & 18
\end{array}\right|\)
= -6(-216 + 220) -3(504 – 440) – 2(-308 + 264)
= – 6(4) – 3(64) – 2(-44)
= -24 – 192 + 88
= 128 ≠ 0
There is a minor of order 3, which is not zero.
∴ ρ(AB) = 3
To find the rank of BA
Order of BA is 3 × 3
∴ ρ(BA) ≤ 3
Consider the third order minor |BA| = \(\left|\begin{array}{ccc}
6 & 1 & 0 \\
-12 & -2 & 0 \\
4 & 4 & -4
\end{array}\right|\)
= 6(8 – 0) – 1(48 – 0) + 0(-48 + 8)
= 6(8) – 1(48) + 0(-40)
= 48 – 48 + 0
= 0
Since the third order minor vanishes, therefore P(BA) ≠ 3
Consider a second order minor \(\left|\begin{array}{ll}
-12 & -2 \\
4 & 4
\end{array}\right|\) = -48 + 8 = -40 ≠ 0
There is a minor of order 2 which is not zero
∴ ρ(BA) = 2
![]()
Question 3.
Solve the following system of equations by rank method
x + y + z = 9, 2x + 5y + 7z = 52, 2x – y – z = 0
Solution:
x + y + z = 9
2x + 5y + 7z = 52
2x – y – z = 0
The matrix equation corresponding to the given system is
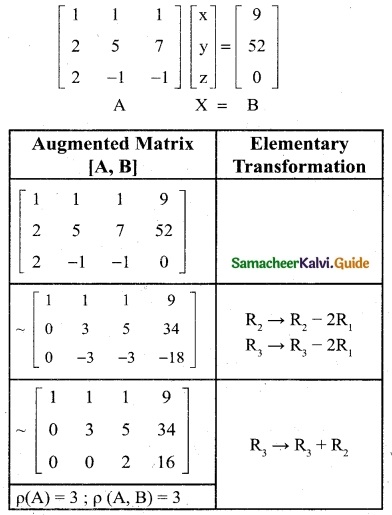
Obviously the last equivalent matrix is in the echelon form. It has three non-zero rows.
P(A) = P (A, B) = 3 = Number of unknowns
The given system is consistent and has unique solution.
To find the solution, let us rewrite the above ech-elon form into the matrix form.
\(\left[\begin{array}{lll}
1 & 1 & 1 \\
0 & 3 & 5 \\
0 & 0 & 2
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
9 \\
34 \\
16
\end{array}\right]\)
x + y + z = 9 ……..(1)
3y + 5z = 34 ……… (2)
2z = 16 ……… (3)
z = \(\frac { 16 }{ 2 }\) = 8
z = 8
Substitute z = 8 in eqn (2)
3y + 5 (8) = 34
3y + 40 = 34
3y = 34 – 40
3y = -6
y = -2
Substitute y = -2 and z = 8 in eqn (1)
x = (-2) + 8 = 9
x + 6 = 9
x = 9 – 6
x = 3
∴ x = 3, y = -2, z = 8
![]()
Question 4.
Show that the equations 5x + 3y + 7z = 4, 3x + 26y + 2z = 9, 7x + 2y + 10z = 5 are consistent and solve them by rank method.
Solution:
5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
The matrix equation corresponding to the given systematic
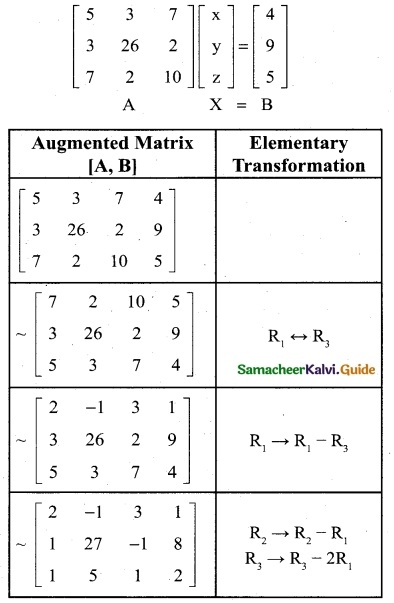
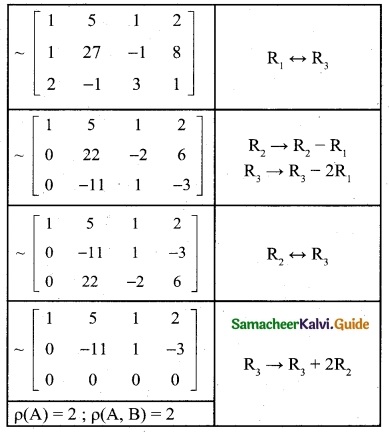
Obviously, the last equivalent matrix is in the echelon form. It has two non-zero rows.
P([A, B]) = 2 ; P(A) = 2
P(A) = P ([A, B]) = 2 < Number of unknowns
The given system is consistent and has infinitely many solutions.
The given system is equivalent to the matrix equation
\(\left[\begin{array}{lll}
1 & 5 & 1 \\
0 & -11 & 1 \\
0 & 0 & 0
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
2 \\
-3 \\
0
\end{array}\right]\)
x + 5y + z = 2 ……. (1)
-11y + z = -3 ……… (2)
let z = k

Where K ε R
![]()
Question 5.
Show that the following system of equations have unique solutions:
x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6 by rank method.
Solution:
x + y + z = 3
x + 2y + 3z = 4
x + 4y + 9z = 6
The matrix equation corresponding to the given system is
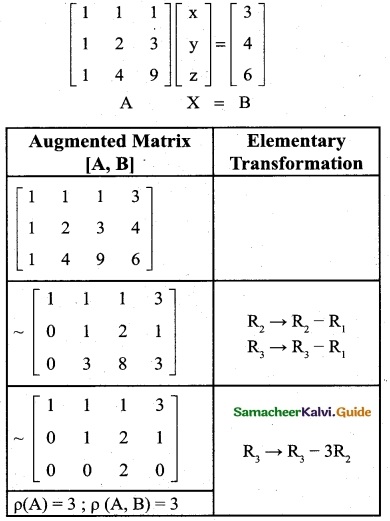
The last equivalent matrix is in the echelon form [A, B] has 3 non-zero rows and [A] has 3 non-zero rows.
p([A,B]) = 3; ρ(A) = 3
ρ([A, B]) = ρ(A) = No. of unknowns
∴ The system of equations have unique solution.
![]()
Question 6.
For what values of the parameter λ, will the following equations fail to have unique solution:
3x – y + λz = 1, 2x + y + z = 2, x + 2y – λz = -1
Solution:
3x – y + λz = 1
2x + y + z = 2
x + 2y – λz = -1
The matrix equation corresponding to the given system is
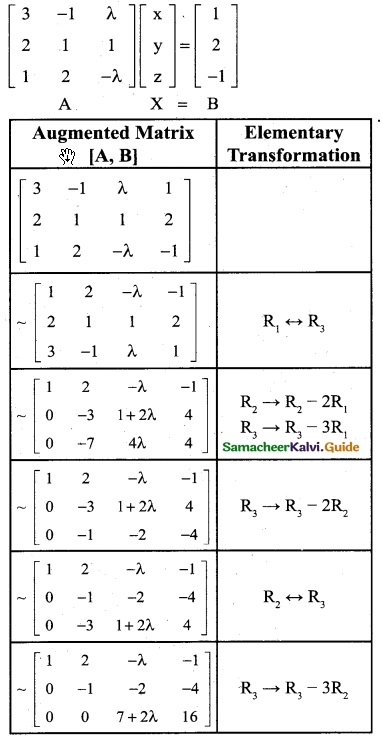
If the equations fail to have unique solution.
ρ(A) ≠ ρ(A, B)
ρ(A, B) = 3
ρ(A) ≠ 3
Therefore 7 + 2λ = 0
2λ = -7 and λ = -7/2
![]()
Question 7.
The price of three commodities. X, Y, and Z are x,y, and z respectively Mr. Anand purchases 6 units of Z and sells 2 units of Y. Mr. Amar purchases a unit of Y and sells 3 units of X and 2 units of Z. Mr. Amit purchases a unit of X and sells 3 units of Y and a unit of Z. In the process they earn Rs 5,000/-, Rs 2,000/- and Rs 5,500/- respectively. Find the prices per unit of three commodities by the rank method.
Solution:
Let the equations for Mr. Anand, Mr. Amar, and Mr. Amit are
2x + 3y – 6z = 5000
3x – y + 2z = 2000
-x + 3y + z = 5500 respectively
The matrix equation corresponding to the given system is

∴ The given system is equivalent to the matrix equation
\(\left[\begin{array}{lll}
-1 & 4 & -8 \\
0 & 1 & -2 \\
0 & 0 & 7
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
3000 \\
1000 \\
3500
\end{array}\right]\)
-x + 4y – 8z = 3000 …….. (1)
y – 2z = 1000 ………. (2)
7z = 3500 ……….. (3)
Eqn (3) ⇒ z = \(\frac { 3500 }{ 7 }\)
∴ z = 500
Eqn (2) ⇒ y – 2(500) = 1000
y = 1000 + 1000
∴ y = 2000
Eqn (1) ⇒ -x + 4 (2000) – 8 (500) = 3000
-x + 8000 – 4000 = 3000
-x + 4000 = 3000
-x = 3000 – 4000
-x = – 1000
∴ x = 1000
The price of three commodities, x, y and z are Rs. 1000; Rs. 2000 and Rs. 500 respectively.
![]()
Question 8.
An amount of Rs 5,000/- is to be deposited in three different bonds bearing 6%, 7%, and 8% per year respectively. Total annual income is Rs 358/-, If the income from the first two investments is Rs 70/- more than the income from the third, then find the amount of investment in each bond by the rank method.
Solution:
Let the three different bonds be x, y, and z
x + y + z = 5000 …….. (1)
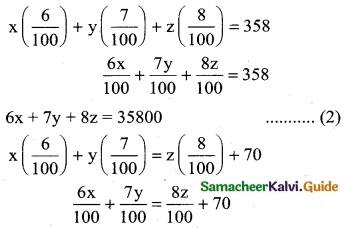
6x + 7y = 8z + 7000
6x + 7y – 8z = 7000 ……… (3)
The matrix equation corresponding to the given system is
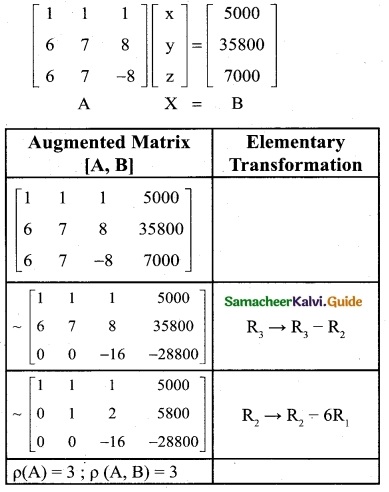
∴ The given system is equivalent to the matrix equation
\(\left[\begin{array}{lll}
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 0 & -16
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] =\left[\begin{array}{c}
5000 \\
5800 \\
-28800
\end{array}\right]\)
x + y + z = 5000 ……… (1)
y + 2z = 5800 …….. (2)
-16z = -28800 ……… (3)
eqn (3) ⇒ z = \(\frac { -28800 }{ -16 }\)
∴ z = 1800
eqn (2) ⇒ y + 2(1800) = 5800
y + 3600 = 5800
y = 5800 – 3600
∴ y = 2200
eqn (1) ⇒ x + 2200 + 1800 = 5000
x + 4000 = 5000
x = 5000 – 4000
∴ x = 1000
The amount of investment in each bond is Rs 1000, Rs 2200 and Rs 1800.
![]()