Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.3
Question 1.
Given the following pay – off matrix (in rupees) for three strategies and two states for nature.
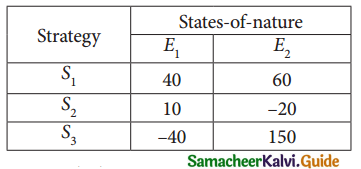
Select a strategy using each of the following rule (i) Maximin (ii) Minimax
Solution:
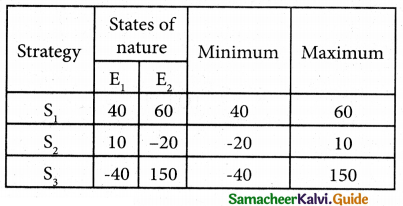
(i) Max min
Max ( 40, -20, -40) = 40. Since the maximum pay-off is 40, the alternative S, is selected.
(ii) Minimax
min (60, 10, 150) = 10, Since the minimum payoff is 10. the alternative S2 is selected.
![]()
Question 2.
A farmer wants to decide which of three crops he should plant on his 100 – acre farm. The profit from each is dependent on the rainfall during the growing season. The farmer has categorized the amount of rainfall as high medium and low. His estimated profit for each is shown in the table.
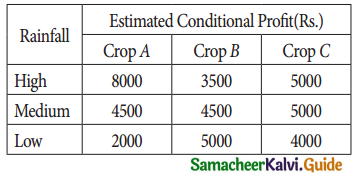
In the farmer wishes to plant only crop, decide which should be his best crop using (i) Maximin (ii) Minimax
Solution:
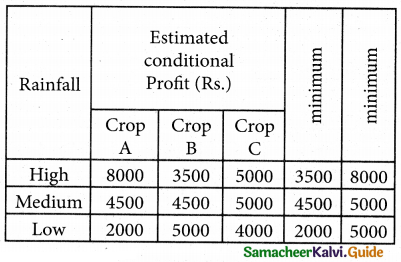
(i) Maximin
Max ( 3500, 4500, 2000) = 4500. Since the maximum pay-off is 4500, the alternative ‘Medium’, is selected.
(ii) Minimax
min (8000, 5000, 5000) = 5000, Since the minimum pay-off is 5000. the alternatives both ‘Medium’ and ‘Low’ are selected.
![]()
Question 3.
The research department of Hindustan Ltd. has recommended to pay marketing department to launch a shampoo of three different types. The marketing types of shampoo to be launched under the following T estimated pay-offs for various level of sales.
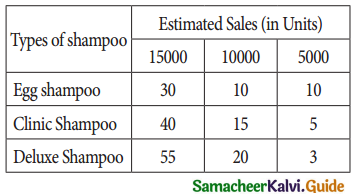
What will be the marketing manager’s decision if (i) Maximin and (ii) Minimax principle applied?
Solution:
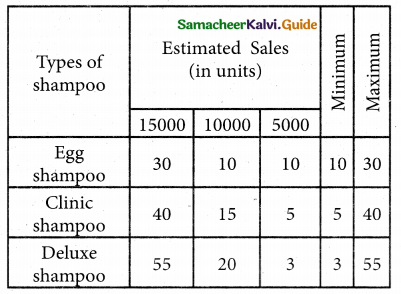
(i) Maximin
Max ( 10, 5, 3) = 10. Since the maximum pay of is 10, “Egg Shampoo”, is selected.
(ii) Minimax
min (30, 40, 55) = 30, Since the minimum pay-off is 30. the alternative “Egg Shampoo” is selected
![]()
Question 4.
Following pay – off matrix, which is the optimal decision under of the following rule (i) maximin (ii) minimax
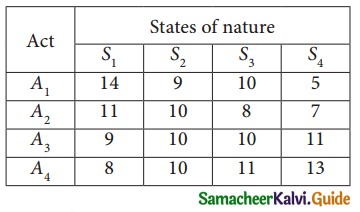
Solution:
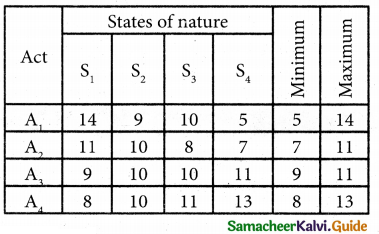
(i) Maximin
Max ( 5, 7, 9, 8) = 5. Since the maximum pay-off is 5, the alternative A1 is selected.
(ii) Minimax
min (14, 11, 11, 13) = 11, Since the minimum pay-off is 11. the alternative alternatives A2 and A3 are selected.
![]()