Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 2 Integral Calculus I Ex 2.12 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.12
Choose the most suitable answer from the given four alternatives:
Question 1.
∫\(\frac { 1 }{x^3}\) dx is
(a) \(\frac { -3 }{x^2}\) + c
(b) \(\frac { -1 }{2x^2}\) + c
(c) \(\frac { -1 }{3x^2}\) + c
(d) \(\frac { -2 }{x^2}\) + c
Solution:
(b) \(\frac { -1 }{2x^2}\) + c
Hint:
∫\(\frac { 1 }{x^3}\) dx = ∫x-3 dx = [ \(\frac { x^{-3+1} }{-3+1}\) ] + c
= (\(\frac { x^{-2} }{-2}\)) + c = \(\frac { -1 }{2x^2}\) + c
Question 2.
∫2x dx is
(a) 2x log 2 + c
(b) 2x + c
(c) \(\frac { 2^x }{log 2}\) + c
(d) \(\frac { log 2 }{2^x}\) + c
Solution:
(c) \(\frac { 2^x }{log 2}\) + c
Hint:
∫2x dx = ∫ax dx = \(\frac { a^x }{log a}\) + c
![]()
Question 3.
∫\(\frac { sin 2x }{2 sin x}\) dx is
(a) sin x + c
(b) \(\frac { 1 }{2}\) sin x + c
(c) cos x + c
(d) \(\frac { 1 }{2}\) cos x + c
Solution:
(a) sin x + c
Hint:
∫\(\frac { sin 2x }{2 sin x}\) dx = ∫\(\frac { 2sin x cos x }{2 sin x}\) dx
= ∫cos x dx
= sin x + c
Question 4.
∫\(\frac { sin 5x-sin x }{cos 3x}\) dx is
(a) -cos 2x + c
(b) -cos 2x – c
(c) –\(\frac { 1 }{4}\) cos 2x + c
(d) -4 cos 2x + c
Solution:
(a) -cos 2x + c
Hint:
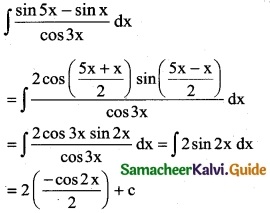
![]()
Question 5.
∫\(\frac { log x}{x}\) dx, x > 0 is
(a) \(\frac { 1 }{2}\) (log x)² + c
(b) –\(\frac { 1 }{2}\) (log x)²
(c) \(\frac { 2 }{x^2}\) + c
(d) \(\frac { 2 }{x^2}\) – c
Solution:
(a) \(\frac { 1 }{2}\) (log x)² + c
Hint:
∫\(\frac { log x}{x}\) dx, x > 0
∫ tdt = [ \(\frac { t^2 }{2}\) ] + c
= \(\frac { (log x)^2 }{2}\) + c
let t = log x
\(\frac { dt }{dx}\) = \(\frac { 1 }{x}\)
dt = \(\frac { 1 }{x}\) dx
Question 6.
∫\(\frac { e^x }{\sqrt{1+e^x}}\) dx is
(a) \(\frac { e^x }{\sqrt{1+e^x}}\) + c
(b) 2\(\sqrt{1+e^x}\) + c
(c) \(\sqrt{1+e^x}\) + c
(d) ex\(\sqrt{1+e^x}\) + c
Solution:
(b) 2\(\sqrt{1+e^x}\) + c
Hint:

![]()
Question 7.
∫\(\sqrt { e^x}\) dx is
(a) \(\sqrt { e^x}\) + c
(b) 2\(\sqrt { e^x}\) + c
(c) \(\frac { 1 }{2}\) \(\sqrt { e^x}\) + c
(d) \(\frac { 1 }{2\sqrt { e^x}}\) + c
Solution:
(b) 2\(\sqrt { e^x}\) + c
Hint:
∫\(\sqrt { e^x}\) dx
= ∫\(\sqrt { e^x}\) dx = ∫(ex)1/2 dx = ∫ ex/2 dx
= \(\frac { e^{x/2} }{1/2}\) + c = 2ex/2 + c
= 2(ex)1/2 + c = 2\(\sqrt { e^x}\) + c
Question 8.
∫e2x [2x² + 2x] dx
(a) e2x x² + c
(b) xe2x + c
(c) 2x²e² + c
(d) \(\frac { x^2e^x }{2}\) + c
Solution:
(a) e2x x² + c
Hint:
∫e2x (2x² + 2x) dx
Let f(x) = x²; f'(x) = 2x and a = 2
= ∫eax [af(x),+ f ’(x)] = eax f(x) + c
= ∫e2x (2x² + 2x) dx = e2x (x²) + c
Question 9.
\(\frac { e^x }{e^x+1}\) dx is
(a) log |\(\frac { e^x }{e^x+1}\)| + c
(b) log |\(\frac { e^x+1 }{e^x}\)| + c
(c) log |ex| + c
(d) log |ex + 1| + c
Solution:
(d) log |ex + 1| + c
Hint:
∫\(\frac { e^x }{e^x+1}\) dx
= ∫\(\frac { dt }{t}\)
= log |t| + c
= log |ex + 1| + c
take t = ex + 1
\(\frac { dt }{dx}\) = ex
dt = ex dx
![]()
Question 10.
∫\(\frac { 9 }{x-3}-\frac { 1 }{x+1}\) dx is
(a) log |x – 3| – log|x + 1| + c
(b) log|x – 3| + log|x + 1| + c
(c) 9 log |x – 3| – log |x + 1| + c
(d) 9 log |x – 3| + log |x + 1| + c
Solution:
(c) 9 log |x – 3| – log |x + 1| + c
Hint:
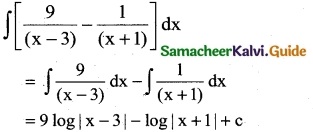
Question 11.
∫\(\frac { 2x^3 }{4+x^4}\) dx is
(a) log |4 + x4| + c
(b) \(\frac { 1 }{2}\) log |4 + x4| + c
(c) \(\frac { 1 }{2}\) log |4 + x4| + c
(d) log |\(\frac { 2x^3 }{4+x^4}\) + c
Solution:
(b) \(\frac { 1 }{2}\) log |4 + x4| + c
Hint:
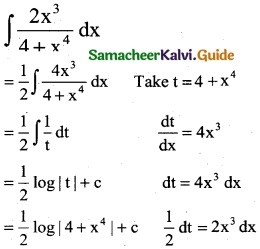
Question 12.
∫\(\frac { dx }{\sqrt{x^2-36}}\) is
(a) \(\sqrt{x^2-36}\) + c
(b) log |x + \(\sqrt{x^2-36}\)| + c
(c) log |x – \(\sqrt{x^2-36}\)| + c
(d) log |x² + \(\sqrt{x^2-36}\)| + c
Solution:
(b) log |x + \(\sqrt{x^2-36}\)| + c
Hint:
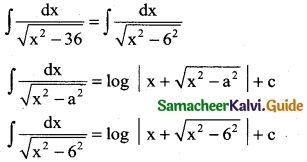
![]()
Question 13.
∫\(\frac { 2x+3 }{\sqrt{x^2+3x+2}}\) dx is
(a) \(\sqrt{x^2+3x+2}\) + c
(b) 2\(\sqrt{x^2+3x+2}\) + c
(c) \(\sqrt{x^2+3x+2}\) + c
(d) \(\frac { 2 }{3}\) (x² + 3x + 2) + c
Solution:
(b) 2\(\sqrt{x^2+3x+2}\) + c
Hint:

Question 14.
\(\int_{0}^{4}\) (2x + 1) dx is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2
Hint:
\(\int_{0}^{4}\) (2x + 1) dx
= [2(\(\frac { x^2 }{2}\)) + x]\(_{0}^{1}\) = [x² + x]\(_{0}^{1}\)
= [(1)² + (1)] – [0] = 2
Question 15.
\(\int_{2}^{4}\) \(\frac { dx }{x}\) is
(a) log 4
(b) 0
(c) log 2
(d) log 8
Solution:
(c) log 2
Hint:
\(\int_{2}^{4}\) \(\frac { dx }{x}\)
\(\int_{2}^{4}\) \(\frac { dx }{x}\) = [log |x|]\(_{0}^{1}\) = log |4| – log |2|
= log[ \(\frac { 4}{2}\) ] = log 2
![]()
Question 16.
\(\int_{0}^{∞}\) e-2x dx is
(a) 0
(b) 1
(c) 2
(d) \(\frac { 1 }{2}\)
Solution:
(d) \(\frac { 1 }{2}\)
Hint:
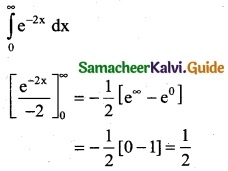
Question 17.
\(\int_{-1}^{1}\) x³ ex4 dx is
(a) 1
(b) 2\(\int_{0}^{1}\) x³ ex4
(c) 0
(d) ex4
Solution:
(c) 0
Hint:
\(\int_{-1}^{1}\) x³ ex4 dx
Let f (x) = x³ex4
f(-x) = (-x)² e(-x)4
= -x² ex4
f(-x) = -f(x)
⇒ f(x) is an odd function
∴ \(\int_{-1}^{1}\) x³ ex4 dx = 0
Question 18.
If f(x) is a continuous function and a < c < b, then \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\) f(x) dx is
(a) \(\int_{a}^{b}\) f(x) dx – \(\int_{a}^{c}\) f(x) dx
(b) \(\int_{a}^{c}\) f(x) dx – \(\int_{a}^{b}\) f(x) dx
(c) \(\int_{a}^{b}\) f(x) dx
(d) 0
Solution:
(c) \(\int_{a}^{b}\) f(x) dx
![]()
Question 19.
The value of \(\int_{-π/2}^{π/2}\) cos x dx is
(a) 0
(b) 2
(c) 1
(d) 4
Solution:
(b) 2
Hint:
\(\int_{-π/2}^{π/2}\) cos x dx
Let f(x) = cos x
f(-x) = cos (-x) = cos (x) = f(x)
∴ f(x) is an even function
\(\int_{-π/2}^{π/2}\) cos x dx = 2 × \(\int_{0}^{π/2}\) cos x dx
= 2 × [sin x]\(_{0}^{-π/2}\) = 2 [sin π/2 – sin 0]
= 2 [1 – 0] = 2
Question 20.
\(\int_{-π/2}^{π/2}\) \(\sqrt {x^4(1-x)^2}\) dx
(a) \(\frac { 1 }{12}\)
(b) \(\frac { -7 }{12}\)
(c) \(\frac { 7 }{12}\)
(d) \(\frac { -1 }{12}\)
Solution:
(a) \(\frac { 1 }{12}\)
Hint:

Question 21.
If \(\int_{0}^{1}\) f(x) dx = 1, \(\int_{0}^{1}\) x f(x) dx = a and \(\int_{0}^{1}\) x² f(x) dx = a², then \(\int_{0}^{1}\) (a – x)² f(x) dx is
(a) 4a²
(b) 0
(c) a²
(d) 1
Solution:
(b) 0
Hint:
\(\int_{0}^{1}\) (a – x)² f(x) dx
= \(\int_{0}^{1}\) [a² +x² – 2ax] f(x) dx
= \(\int_{0}^{1}\) a² + f (x) dx + \(\int_{0}^{1}\) x² f (x) dx – 2a\(\int_{0}^{1}\) x f(x) dx
= a²(1) + a² – 2a(a) – 2a² – 2a² = 0
![]()
Question 22.
The value of \(\int_{2}^{3}\) f(5 – x) dx – \(\int_{2}^{3}\) f(x) dx is
(a) 1
(b) 0
(c) -1
(d) 5
Solution:
(b) 0
Hint:
\(\int_{2}^{3}\) f(5 – x) dx – \(\int_{2}^{3}\) f(x) dx
Using the property
= \(\int_{2}^{3}\) f(x) dx = \(\int_{a}^{b}\) f(a + b – x) dx
= \(\int_{2}^{3}\) f (5 – x) – \(\int_{2}^{3}\) f (5 – x) dx
= 0
Question 23.
\(\int_{0}^{4}\) (√x + \(\frac { 1 }{√x}\)), dx is
(a) \(\frac { 20 }{3}\)
(b) \(\frac { 21 }{3}\)
(c) \(\frac { 28 }{3}\)
(d) \(\frac { 1 }{3}\)
Solution:
(c) \(\frac { 28 }{3}\)
Hint:

Question 24.
\(\int_{0}^{π/3}\) tan x dx is
(a) log 2
(b) 0
(c) log √2
(d) 2 log 2
Solution:
(a) log 2
Hint:
\(\int_{0}^{π/3}\) tan x dx
= ∫tan x dx
= ∫\(\frac { sin x }{cos x}\) dx
= -∫\(\frac { -sin x }{cos x}\) dx
= -log |cos x| + c
= log sec x + c
= [log (sec x)]\(_{0}^{π/3}\)
= log [(sec π/3) – log (sec 0)]
= log (2) – log (1)
= log 2 – (0) = log 2
![]()
Question 25.
Using the factorial representation of the gamma function, which of the following is the solution for the gamma function Γ(n) when n = 8
(a) 5040
(b) 5400
(c) 4500
(d) 5540
Solution:
(a) 5040
Hint:
\(\Upsilon\) (8) = 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
Question 26.
Γ(n) is
(a) (n – 1)!
(b) n!
(c) n Γ (n)
(d) (n – 1) Γ(n)
Solution:
(a) (n – 1)!
Hint:
Γ(n) = Γ(n – 1) + 1 = (n – 1)!
Question 27.
Γ(1) is
(a) 0
(b) 1
(c) n
(d) n!
Solution:
(b) 1
Hint:
\(\Upsilon\) (1) = 0! = 1
![]()
Question 28.
If n > 0, then Γ(n) is
(a) \(\int_{0}^{1}\) e-x xn-1 dx
(b) \(\int_{0}^{1}\) e-x xⁿ dx
(c) \(\int_{0}^{∞}\) ex x-n dx
(d) \(\int_{0}^{∞}\) e-x xn-1 dx
Solution:
(d) \(\int_{0}^{∞}\) e-x xn-1 dx
Question 29.
Γ(\(\frac { 3 }{2}\))
(a) √π
(b) \(\frac { √π }{2}\)
(c) 2√π
(d) \(\frac { 3 }{2}\)
Solution:
(b) \(\frac { √π }{2}\)
Hint:
\(\Upsilon\) (3/2) = \(\frac { 2 }{2}\) \(\Upsilon\) [ \(\frac { 3 }{2}\) ]
= \(\frac { 3 }{2}\) √π
Question 30.
\(\int_{0}^{∞}\) x4 e-x dx is
(a) 12
(b) 4
(c) 4!
(d) 64
Solution:
(b) \(\frac { √π }{2}\)
Hint:
\(\int_{0}^{∞}\) x4 e-x dx
= ∫xⁿ e-ax dx = \(\frac { n! }{a{n+1}}\)
= \(\frac { 4! }{(1)^{n+1}}\)
= \(\frac { 4! }{(1)^5}\)
= 4!
![]()
Must Read: