Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.1
Question 1.
Using Interation, find the area of the region bounded the line given is 2y + x = 8, the x axis and the lines x = 2, x = 4.
Solution:
The equation of the line given is 2y + x = 8
⇒ 2y = 8 – x ⇒ y = \(\frac { 8-x }{2}\)
y = 4 – \(\frac { x }{2}\)
Also x varies from 2 to 4
The required Area

= (16 – 4) – (8 – 1)
= 12 – 7 = 5 sq.units
![]()
Question 2.
Find the area bounded by the lines y – 2x – 4 = 0, y = 0, y = 3 and the y-axis.
Solution:
The equation of the line given is y – 2x – 4 = 0
⇒ 2x = y – 4 ⇒ x = \(\frac { y-4 }{2}\)
∴ x = \(\frac { y }{2}\) – 2
Also y varies from 1 to 3
Required Area
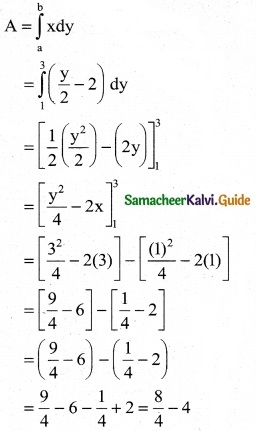
= 2 – 4 = -2
Area can’t be in negative.
∴ Area = 2 sq.units
![]()
Question 3.
Calculate the area bounded by the parabola y² = 4ax and its latus rectum.
Solution:
Given parabola is y2 = 4ax
Its focus is (a, 0)
Equation of latus rectum is x = a
The parabola is symmetrical about the x-axis
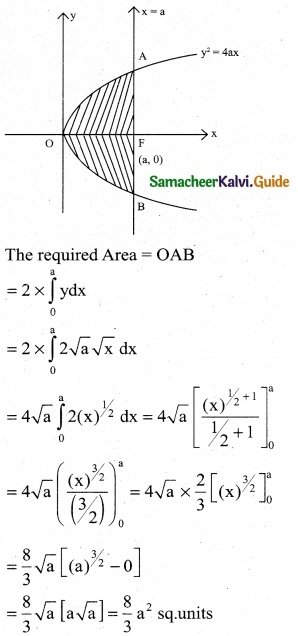
![]()
Question 4.
Find the area bounded by the line y = x and x-axis and the ordinates x = 1, x = 2
Solution:
The equation of the given line is y = x and x varies from 1 to 2
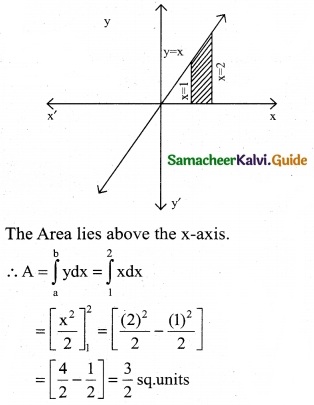
Question 5.
Using integration, find the area of the region bounded by the line y – 1 = x, the x-axis and the ordinates x = -2, x = 3.
Solution :
The equation of given line is y – 1 = x
y = x + 1
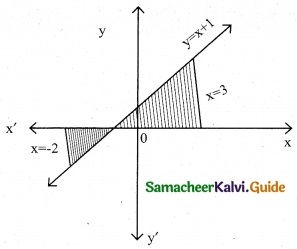
The line y = x + 1 meets the x-axis at x = -1
Since x varies from -2 to 3
Hence a part of lies below the x-axis and the other part lies above the x-axis.
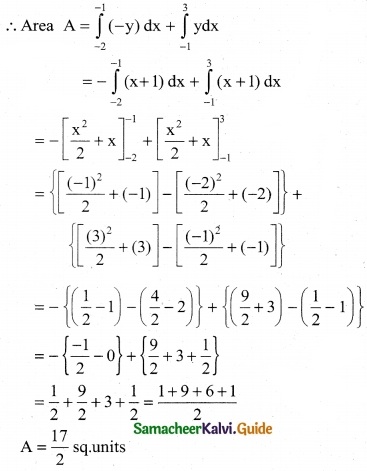
![]()
Question 6.
Find the area of the region lying in the first quadrant bounded by the region y = 4x², x = 0, y = 0 and y = 4
Solution:
The equation of a parabola given is y = 4x²
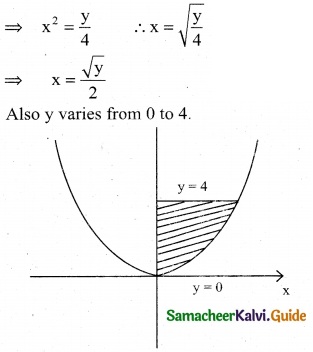
Area of the region lying in the first quadrant

![]()
Question 7.
Find the area bounded by the curve y = x² and the line y = 4
Solution:
Equation of the curve y = x² ………. (1)
Equation of the line y = 4 ………. (2)
Solving equation (1) & (2)
x² = 4 ⇒ x = ± 2

![]()
Read More: