Samacheer Kalvi 12th Business Maths Guide Chapter 4 Differential Equations Ex 4.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 4 Differential Equations Ex 4.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.3

Question 1.
Solve:
x\(\frac { dy }{dx}\) = x + y
Solution:
x\(\frac { dy }{dx}\) = x + y
x\(\frac { dy }{dx}\) = x + y ⇒ \(\frac { dy }{dx}\) = \(\frac { x+y }{x}\) ……… (1)
It is a homogeneous differential equation, Same degree in x and y

Integrating on both sides
∫\(\frac { 1 }{x}\) dx = ∫dv
log x = v + c ⇒ x = e^(v+c)
x = e^v.e^c
x = e^v. c ⇒ x = ce^v [⇒ v = \(\frac { y }{x}\)]
⇒ x = ce^y/x

Question 2.
(x – y) \(\frac { dy }{dx}\) = x + 3y
Solution:
(x – y) \(\frac { dy }{dx}\) = x + 3y
\(\frac { dy }{dx}\) = \(\frac { x+3y }{(x-y)}\) ……… (1)
It is a homogeneous differential equation same degree in x and y

Integrating on both sides

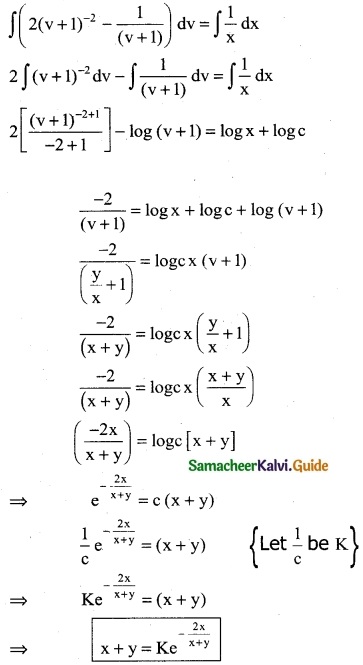
Question 3.
x\(\frac { dy }{dx}\) – y = \(\sqrt { x^2+y^2}\)
Solution:

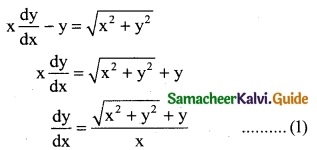
It is a homogeneous differential equation, same degree in x and y

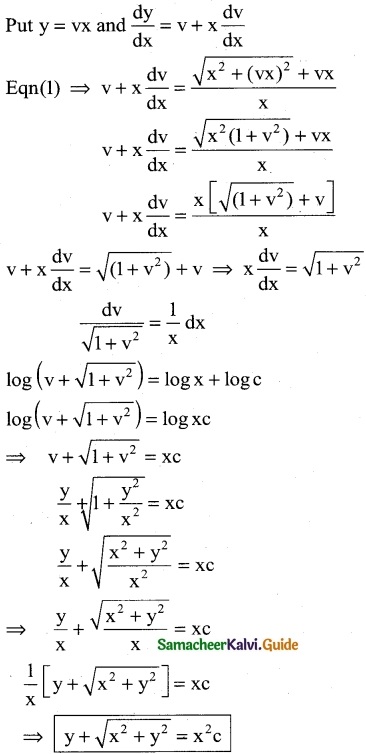
Question 4.
\(\frac { dy }{dx}\) = \(\frac { 3x-2y }{2x-3y}\)
Solution:
\(\frac { dy }{dx}\) = \(\frac { 3x-2y }{2x-3y}\) …….. (1)
It is a homogeneous differential equation same degree in x and y

Integrating on both sides

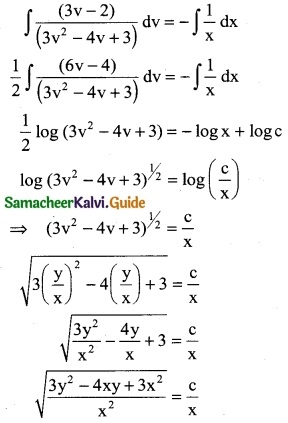
Squaring on both sides

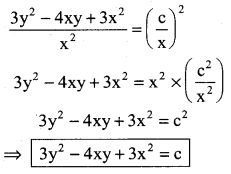
Question 5.
(y² – 2xy) dx = (x² – 2xy)dy
Solution:
(y² – 2xy) dx = (x² – 2xy)dy

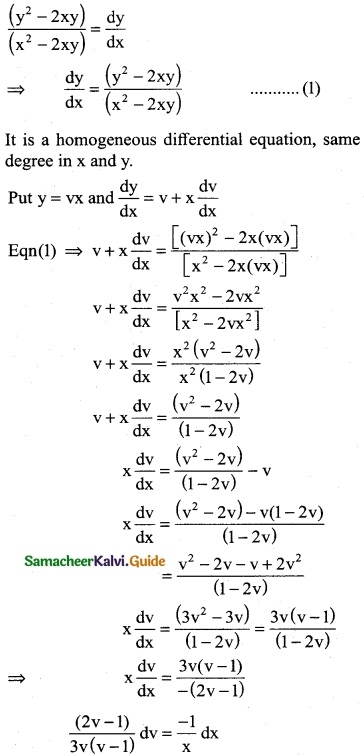
Integrating on both sides

Cubing on both sides

Question 6.
The slope of the tangent to a curve at any point (x, y) on it is given by (y³ – 2yx²) dx + (2xy² – x³) dy = 0 and the curve passes throngh (1, 2). Find the equation of the curve.
Solution:
Given that equation of the slope of tangent
(y³ – 2yx²) dx + (2xy² – x²) dy = 0
(2xy² – x³) dy = – (y³ – 2yx²) dx
(2xy² – x³) dy = (2yx² – y³) dx
\(\frac { dy }{dx}\) = \(\frac { (2yx^2-y^3) }{(2xy^2-x^3)}\) ………. (1)
It is a homogeneous differential equation same degree in x and y.

⇒ 2v² – 1 = A(v² – 1) + B(v) (v + 1) + C(v) (v – 1) ………. (4)
Put v = 0 in (2)
-1 = A(-1) ⇒ A = 1
Put v = -1
2(-1)² – 1 = [A(-1)² -1] + B(0) + C(-1) (-1 -1)
2 – 1 = A(0) + B(0) + C(-1) (-2)
1 = 2C ⇒ C = 1/2
Put v = 1
2(1)² – 1 = [A(1)² – 1] + B(1) (1 +1) + C(1)(1 – 1)
2 – 1 = A(0) + B(2) + C(0)
2B = 1 ⇒ B = 1/2
Substitute A = 1, B = 1/2 and C = 1/2 in (1)

Question 7.
An electric manufacturing company makes small household switchs. The company estimates the marginal revenue function for these switches to be (x² + y²) dy = xy dx where x represents the number of units (in thounsands). What is the total revenue function?
Solution:
Given
Marginal revenue for the switches
(x² + y²) dy = xy dx
\(\frac { dy }{dx}\) = \(\frac { xy }{(x^2+y^2)}\) ……… (1)
It is a homogeneous differential equation same degree in x and y.

Integrating on both sides

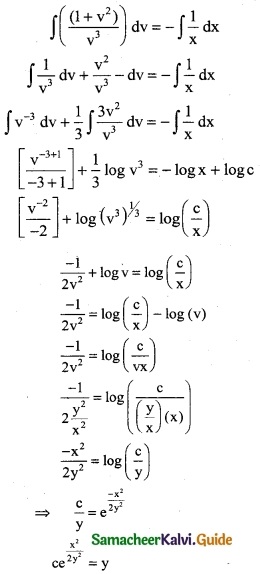
The total revenue function is
⇒ y = ce^{\(\frac { x^2 }{2y^2}\)}