Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 4 Differential Equations Ex 4.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.4
Question 1.
\(\frac { dy }{dx}\) – \(\frac { dy }{dx}\) = x
Solution:
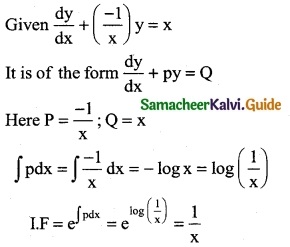
The required solution is

![]()
Question 2.
\(\frac { dy }{dx}\) + y cos x = sin x cos x
Solution:
It is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = cos x; Q = sin x cos x
∫Pdx = ∫cos x dx = sin x
I.F = e∫pdx = esinx
The required solution is
Y(I.F) = ∫Q (IF) dx + c
Y(esinx) = ∫Q (I-F) dx + c
y (esinx) = ∫sin x cos x esinx dx + c

![]()
Question 3.
x\(\frac { dy }{dx}\) + 2y = x4
Solution:
The given equation can be reduced to
\(\frac { dy }{dx}\) + \(\frac { 2y }{x}\) = x³
It is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = \(\frac { 2 }{x}\); Q = x³
∫pdx = ∫\(\frac { 2 }{x}\)dx = 2∫\(\frac { 1 }{x}\)dx = 2log x – log x²
I.F = e∫Pdx = elogx² = x²
The required solution is
y(I.F) = ∫Q (IF) dx + c
y(x²) = ∫x³ (x²) dx + c
x²y = ∫x5 dx + c
x²y = \(\frac { x^6 }{6}\) + c
![]()
Question 4.
\(\frac { dy }{dx}\) + \(\frac { 3x^2 }{1+x^3}\) = \(\frac { 1+x^2 }{1+x^3}\)
Solution:

Question 5.
\(\frac { dy }{dx}\) + \(\frac { y }{x}\) = xex
Solution:
\(\frac { dy }{dx}\) + py = Q
Here P = \(\frac { 1 }{x}\); Q = xex
∫Pdx = ∫\(\frac { 1 }{x}\) dx = log x
I.F = e∫Pdx = elog = x
The required solution is
y (I.F) = ∫Q (I.F) dx + c

![]()
Question 6.
\(\frac { dy }{dx}\) + y tan x = cos³ x
Solution:
It is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = tan x; Q = cos³ x
∫Pdx = ∫tan x dx = ∫\(\frac { sin x }{cos x}\) dx = -∫\(\frac { -sin x }{cos x}\) dx
= -log cos x = log sec x
I.F = e∫Pdx = elog sec x = sec x
The required solution is
y(I.F) = ∫Q(I.F) dx + c
y (sec x) = ∫cos³x (sec x) dx + c
y(sec x) = ∫cos³x \(\frac { 1 }{cos x}\) dx + c
y (sec x) = ∫cos²x dx + c
y (sec x)= ∫(\(\frac { 1+cos 2x }{2}\)) dx + c
y (sec x) = \(\frac { 1 }{2}\) ∫(1 + cos2x) dx + c
y (sec x) = \(\frac { 1 }{2}\) [x + \(\frac { sin2x }{2}\)] + c
![]()
Question 7.
If \(\frac { dy }{dx}\) + 2y tan x = sinx and if y = 0 when x = π/3 express y in terms of x
Solution:
\(\frac { dy }{dx}\) + 2y tan x = sinx
It is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = 2tan x ; Q = sin x
∫Pdx = ∫2 tan x dx = 2∫tan xdx = 2 log sec x
log sec² x
I.F = e∫Pdx = elog(sec²x) = sec² x
The required solution is
y(I.F) = ∫Q(I.F) dx + c
y (sec² x) = ∫sin x (sec²x) dx + c
y(sec²x) = ∫sin x(\(\frac { 1 }{cos x}\)) sec x dx + c
y sec²x = ∫(\(\frac { sin x }{cos x}\)) sec x dx + c
y(sec²x) = ∫tan x sec x dx + c
⇒ y(sec²x) = sec x + c ………. (1)
If y = 0 when x = /3, then (1) ⇒
0(sec²(π/3)) = sec(π/3) + c
0 = 2 + c
⇒ c = -2
∴ Eqn (1) ⇒ y sec²x = sec x – 2
Question 8.
\(\frac { dy }{dx}\) + \(\frac { y }{x}\) = xex
Solution:
It is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = \(\frac { 1 }{x}\); Q = xex
∫Pdx = ∫\(\frac { 1 }{x}\) dx = log x
I.F = e∫Pdx = elog x = x
The required solution is

![]()
Question 9.
A bank pays interest by contionous compounding, that is by treating the interest rate as the instantaneous rate of change of principal. A man invests Rs 1,00,000 in the bank deposit which accures interest, 8% over year compounded continuously. How much will he get after 10 years?
Solution :
Let P(t) denotes the amount of money in the account at time t. Then the differential equation govemning the growth of money is
\(\frac { dp }{dt}\) = \(\frac { 8 }{100}\)p = 0.08 p
⇒ \(\frac { dp }{p}\) = 0.08 dt
Integrating on both sides
∫\(\frac { dp }{p}\) = ∫0.08 dt
loge P = 0.08 t + c
P = e0.08 t + c
P = e0.08 t. ec
P = C1 e0.08 t ………. (1)
when t = 0, P = Rs 1,00,000
Eqn (1) ⇒ 1,00,000 = C1 e°
C1 = 1,00,000
∴ P = 100000 e0.08 t
At t = 10
P= 1,00,000 . e0.08(10)
= 1,00,000 e0.8 {∵ e0.8 = 2.2255}
= 100000 (2.2255)
p = Rs 2,25,550
![]()