Samacheer Kalvi 12th Business Maths Guide Chapter 4 Differential Equations Ex 4.6

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 4 Differential Equations Ex 4.6 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.6

Choose the most suitable answer from the given four alternatives:

Question 1.
The degree of the differential equation
\(\frac { d^2y }{dx^4}\) – (\(\frac { d^2y }{dx^2}\)) + \(\frac { dy }{dx}\) = 3
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(a) 1
Hint:
Since the power of \(\frac{d^{4} y}{d x^{4}}\) is 1

Question 2.
The order and degree of the differential equation \(\sqrt{\frac { d^2y }{dx^2}}\) = \(\sqrt{\frac { dy }{dx}+5}\) are respectively.
(a) 2 and 2
(b) 3 and 2
(c) 2 and 1
(d) 2 and 3
Solution:
(a) 1
Hint:
Squaring on both sides
\(\frac { d^2y }{dx^2}\) = \(\frac { dy }{dx}\) + 5
Highest order derivative is \(\frac { d^2y }{dx^2}\)
∴ order = 2
Power of the highest order derivative \(\frac { d^2y }{dx^2}\) = 1
∴ degree = 1

Question 3.
The order and degree of the differential equation
(\(\frac { d^2y }{dx^2}\))^3/2 – \(\sqrt{(\frac { dy }{dx})}\) – 4 = 0
(a) 2 and 6
(b) 3 and 6
(c) 1 and 4
(d) 2 and 4
Solution:
(a) 2 and 6
Hint:

Highest order derivative is \(\frac { d^2y }{dx^2}\)
∴ Order = 2
Power of the highest order derivative \(\frac { d^2y }{dx^2}\) is
∴ degree = 6

Question 4.
The differential equation (\(\frac { dx }{dy}\))³ + 2y^1/2 = x
(a) of order 2 and degree 1
(b) of order 1 and degree 3
(c) of order 1 and degree 6
(d) of order 1 and degree 2
Solution:
(b) of order 1 and degree 3
Hint:

Highest order derivative is \(\frac { dy }{dx}\)
∴ order = 1
Power of the highest order derivative \(\frac { dy }{dx}\) is 3
∴ degree = 3

Question 5.
The differential equation formed by eliminating a and b from y = ae^x + be^-x
(a) \(\frac { d^2y }{dx^2}\) – y = 0
(b) \(\frac { d^2y }{dx^2}\) – \(\frac { dy }{dx}\)y = 0
(c) \(\frac { d^2y }{dx^2}\) = 0
(d) \(\frac { d^2y }{dx^2}\) – x = 0
Solution:
(a) \(\frac { d^2y }{dx^2}\) – y = 0
Hint:

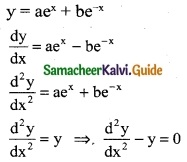
Question 6.
If y = ex + c – c³ then its differential equation is
(a) y = x\(\frac { dy }{dx}\) + \(\frac { dy }{dx}\) – (\(\frac { dy }{dx}\))³
(b) y + (\(\frac { dy }{dx}\))³ = x \(\frac { dy }{dx}\) – \(\frac { dy }{dx}\)
(c) \(\frac { dy }{dx}\) + (\(\frac { dy }{dx}\))³ – x\(\frac { dy }{dx}\)
(d) \(\frac { d^3y }{dx^3}\) = 0
Solution:
(a) y = x\(\frac { dy }{dx}\) + \(\frac { dy }{dx}\) – (\(\frac { dy }{dx}\))³
Hint:
y = cx + c – c³ ……… (1)
\(\frac { dy }{dx}\) = c
(1) ⇒ y = x\(\frac { dy }{dx}\) + \(\frac { dy }{dx}\) – (\(\frac { dy }{dx}\))³

Question 7.
The integrating factor of the differential equation \(\frac { dy }{dx}\) + Px = Q is
(a) e^∫pdx
(b) e^∫Pdx
(c) e^∫Pdy
(d) e^∫pdy
Solution:
(d) e^∫pdy

Question 8.
The complementary function of (D² + 4) y = e^2x is
(a) (Ax+B)e^2x
(b) (Ax+B)e^-2x
(c) A cos2x + B sin2x
(d) Ae^-2x + Be^2x
Solution:
(c) A cos2x + B sin2x
Hint:
A.E = m² + 4 = 0 ⇒ m = ±2i
C.F = e^0x (A cos 2x + B sin 2x)

Question 9.
The differential equation of y = mx + c is (m and c are arbitrary constants)
(a) \(\frac { d^2y }{dx^2}\) = 0
(b) y = x\(\frac { dy }{dx}\) + o
(c) xdy + ydx = 0
(c) ydx – xdy = 0
Solution:
(a) \(\frac { d^2y }{dx^2}\) = 0
Hint:
y = mx + c
\(\frac { dy }{dx}\) = m ⇒ \(\frac { d^2y }{dx^2}\) = 0

Question 10.
The particular intergral of the differential equation \(\frac { d^2y }{dx^2}\) – 8\(\frac { dy }{dx}\) + 16y = 2e^4x
(a) \(\frac { x^2e^{4x} }{2!}\)
(b) y = x\(\frac { e^{4x} }{2!}\)
(c) x²e^4x
(d) xe^4x
Solution:
(c) x²e^4x
Hint:

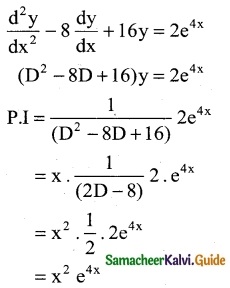
Question 11.
Solution of \(\frac { dx }{dy}\) + Px = 0
(a) x = ce^py
(b) x = ce^-py
(c) x = py + c
(d) x = cy
Solution:
(b) x = ce^-py

Question 12.
If sec^2x x isa na intergranting factor of the differential equation \(\frac { dx }{dy}\) + Px = Q then P =
(a) 2 tan x
(b) sec x
(c) cos 2 x
(d) tan 2 x
Solution:
(a) 2 tan x
Hint:
I.F = sec² x
e^∫pdx = sec²x
∫pdx = log sec² x
∫pdx = 2 log sec x
∫pdx = 2∫tan x dx ⇒ p = 2 tan x

Question 13.
The integrating factor of the differential equation is x \(\frac { dy }{dx}\) – y = x²
(a) \(\frac { -1 }{x}\)
(b) \(\frac { 1 }{x}\)
(c) log x
(c) x
Solution:
(b) \(\frac { 1 }{x}\)
Hint:

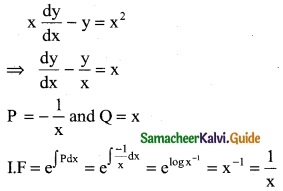
Question 14.
The solution of the differential equation where P and Q are the function of x is
(a) y = ∫Q e^∫pdx dx + c
(b) y = ∫Q e^-∫pdx dx + c
(c) ye^∫pdx = ∫Q e^∫pdx dx + c
(c) ye^∫pdx = ∫Q e^-∫pdx dx + c
Solution:
(c) ye^∫pdx = ∫Q e^∫pdx dx + c

Question 15.
The differential equation formed by eliminating A and B from y = e^-2x (A cos x + B sin x) is
(a) y₂ – 4y₁ + 5 = 0
(b) y₂ + 4y – 5 = 0
(c) y₂ – 4y₁ + 5 = 0
(d) y₂ + 4y₁ – 5 = 0
Solution:
(d) y₂ + 4y₁ – 5 = 0
Hint:
y = e^-2x (A cosx + B sinx)
y e^2x = A cosx + B sinx ………. (1)
y(e^2x) (2) + e^2x \(\frac { dy }{dx}\) = A(-sin x) + B cos x ………. (2)
Differentiating w.r.to x

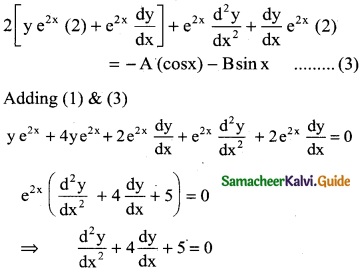
Question 16.
The particular integral of the differential equation f (D) y = e^ax where f(D) = (D – a)²
(a) \(\frac { x^2 }{2}\) e^ax
(b) xe^ax
(c) \(\frac { x }{2}\) e^ax
(d) x² e^ax
Solution:
(a) \(\frac { x^2 }{2}\) e^ax

Question 17.
The differential equation of x² + y² = a²
(a) xdy + ydx = 0
(b) ydx – xdy = 0
(c) xdx – ydx = 0
(d) xdx + ydy = 0
Solution:
(d) xdx + ydy = 0
Hint:
x² + y² = a²
⇒ 2x + 2y \(\frac{d y}{d x}\) = 0
⇒ x dx + y dy = 0

Question 18.
The complementary function of \(\frac { d^y }{dx^2}\) – \(\frac { dy }{dx}\) = 0 is
(a) A + Be^x
(b) (A + B)e^x
(c) (Ax + B)e^x
(d) Ae^x + B
Solution:
(a) A + Be^x
Hint:
A.E is m² – m = 0
⇒ m(m – 1) = 0
⇒ m = 0, 1
CF is Ae^0x + Be^x = A + Be^x

Question 19.
The P.I of (3D² + D – 14) y = 13e^2x is
(a) \(\frac { 1 }{2}\) e^x
(b) xe^2x
(c) \(\frac { x^2 }{2}\) e^2x
(d) Ae^x + B
Solution:
(b) xe^2x
Hint:
(3D² + D – 14) y = 13e^2x

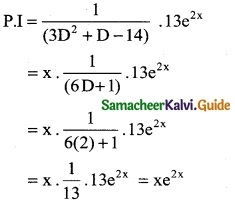
Question 20.
The general solution of the differential equation \(\frac { dy }{dx}\) = cos x is
(a) y = sinx + 1
(b) y = sinx – 2
(c) y = cosx + C, C is an arbitary constant
(d) y = sinx + C, C is an arbitary constant
Solution:
(d) y = sinx + C, C is an arbitary constant
Hint:
\(\frac { dy }{dx}\) = cos x
dy = cos x dx
∫dy = ∫cos x dx ⇒ y = sin x + c

Question 21.
A homogeneous differential equation of the form \(\frac { dy }{dx}\) = f(\(\frac { y }{x}\)) can be solved by making substitution.
(a) y = v x
(b) y = y x
(c) x = v y
(d) x = v
Solution:
(a) y = v x

Question 22.
A homogeneous differential equation of the form \(\frac { dy }{dx}\) = f(\(\frac { x }{y}\)) can be solved by making substitution.
(a) x = v y
(b) y = v x
(c) y = v
(d) x = v
Solution:
(a) y = v x

Question 23.
The variable separable form of \(\frac { dy }{dx}\) = \(\frac { y(x-y) }{x(x+y)}\) by taking y = v x and \(\frac { dy }{dx}\) = v + x \(\frac { dy }{dx}\)
(a) \(\frac { 2v^2 }{1+v}\) dv = \(\frac { dx }{x}\)
(b) \(\frac { 2v^2 }{1+v}\) dv = –\(\frac { dx }{x}\)
(c) \(\frac { 2v^2 }{1-v}\) dv = \(\frac { dx }{x}\)
(d) \(\frac { 1+v }{2v^2}\) dv = –\(\frac { dx }{x}\)
Solution:
(d) \(\frac { 1+v }{2v^2}\) dv = –\(\frac { dx }{x}\)
Hint:

Question 24.
Which of the following is the homogeneous differential equation?
(a) (3x – 5) dx = (4y – 1) dy
(b) xy dx – (x³ + y³) dy = 0
(c) y²dx + (x² – xy – y²) dy = 0
(d) (x² + y) dx (y² + x) dy
Solution:
(c) y²dx + (x² – xy – y²) dy = 0

Question 25.
The solution of the differential equation \(\frac { dy }{dx}\) = \(\frac { y }{x}\) + \(\frac { f(\frac { y }{x}) }{ f(\frac { y }{x}) }\) is
(a) f\(\frac { y }{x}\) = k x
(b) x f\(\frac { y }{x}\) = k
(c) f\(\frac { y }{x}\) = k y
(d) x f\(\frac { y }{x}\) = k
Solution:
(a) f\(\frac { y }{x}\) = k x