Samacheer Kalvi 12th Business Maths Guide Chapter 4 Differential Equations Miscellaneous Problems

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 4 Differential Equations Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Miscellaneous Problems

Question 1.
Suppose that Qd = 30 – 5P + 2\(\frac { dp }{dt}\) + \(\frac { d^2p }{dt^2}\) and Qs = 6 + 3P Find the equilibrium price for market clearance.
Solution :
Qd = 30 – 5P + 2\(\frac { dp }{dt}\) + \(\frac { d^2p }{dt^2}\) and
Qs = 6 + 3P
For market clearance, the required condition is
Qd = Qs

The auxiliary equation is m2 + 2m – 8 = 0
(m + 4) (m – 2) = 0
m = -4, 2
Roots are real and different
C.F = Ae^m₁x + Be^m₂x
C.F = Ae^-4t + Be^2t

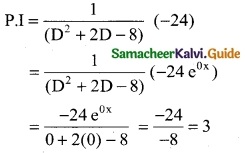
The general solution is y = C.F + P.I
y = Ae^-ut + Be^2t + 3

Question 2.
Form the differential equation having for its general solution y = ax² + bx
Solution:
y = ax² + bx ……….. (1)
Since we have two arbitary constants, differentiative twice.

Question 3.
Solve yx²dx + e^-x dy = 0
Solution:
yx²dx + e^-x dy = 0
e^-x dy = -yx²dx
\(\frac { 1 }{y}\) dy = -x² e^x dx
Integrating on both sides

Question 4.
Solve (x² + y²) dx + 2xy dy = 0
Solution:
(x² + y²) dx + 2xy dy = 0
2xy dy = – (x² + y²) dx
\(\frac { dy }{dx}\) = \(\frac { -(x^2+y^2) }{2xy}\) ………. (1)
This is a homogeneous differential equation

\(\frac { 1 }{3}\) log(3v² + 1) = – logx + logc
log (3v² + 1)^1/3 + log x = log c
logx (3v² + 1)^1/3 = log c
⇒ x (3v² + 1)^1/3 = c
⇒ x[\(\frac { 3y^2 }{x^2}\) + 1]^1/3 = c

Question 5.
Solve x \(\frac { dy }{dx}\) + 2y = x⁴
Solution:

This solution is
y(I.F) = ∫Qx (I.F) dx + c
y(x²) = ∫(x³ × x²) dx + c
yx² = ∫x⁵ dx + c
⇒ yx² = \(\frac { x^6 }{6}\) + c

Question 6.
A manufacturing company has found that the cost C of operating and maintaining the equipment is related to the length’m’ of intervals between overhauls by the equation m² \(\frac { dc }{dm}\) + 2mc = 2 and c = 4 and whem m = 2. Find the relationship between C and m.
Solution:
m² \(\frac { dc }{dm}\) + 2mc = 2
÷ each term by m²
\(\frac { dc }{dm}\) + \(\frac { 2mc }{m^2}\) = \(\frac { 2 }{m^2}\)
\(\frac { dc }{dm}\) + \(\frac { 2c }{m}\) = \(\frac { 2 }{m^2}\)
This is a first order linear differential equation of the form
\(\frac { dc }{dm}\) + Pc = Q where P = \(\frac { 2 }{m}\) and Q = \(\frac { 2 }{m^2}\)
∫Pdm = 2 ∫\(\frac { 1 }{m}\)dm = 2 log m = log m²
I.F = e^∫Pdm = e^logm² = m²
General solution is
C (I.F) = ∫Q × (IF) dm + k
C(m²) = ∫\(\frac { 2 }{m^2}\) × (m²) dm + k
C(m²) = ∫2dm + k
Cm² = 2m + k ……….. (1)
when C = 4 and m = 2, we have
(4) (2)² = 2(2) + k
16 = 4 + k = 12
Equation (1)
Cm² = 2m + 12
Cm² = 2(m + 6)

Question 7.
Solve (D² – 3D + 2) y = e^4x
Solution:
(D² – 3D + 2) y = e^4x
The auxiliary equation is m² – 3m + 2 = 0
(m – 1) (m – 2) = 0
m = 1, 2
The roots are real and different
C.F = Ae^m₁x + Be^m₁x
C.F = Ae^x + Be^2x

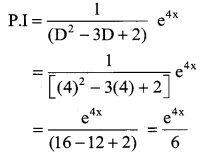
The general solution is y = C.F + P.I
y = Ae^x + Be^2x + \(\frac { e^{4x} }{6}\) ………. (1)
When x = 0; y = 0

Question 8.
Solve \(\frac { dy }{dx}\) + y cos x = 2 cos x
Solution:
\(\frac { dy }{dx}\) + y cos x = 2 cos x
This is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = cos x and Q = 2 cos x
∫Pdx = ∫cos x dx = sin x
I.F = e^∫pdx = e^{sin x}
The solution is
y (I.F) = ∫Q (I.F) dx + c
ye^{sin x} = ∫(2 cos x) e^{sin x} dx

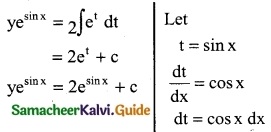
Question 9.
Solve x²ydx – (x³ + y³) dy = 0
Solution:
x²ydx = (x³ + y³) dy = 0
x²ydx = (x³ + y³) dy
\(\frac { dy }{dx}\) = \(\frac { x^2y }{(x^3+y^3)}\) ……… (1)
This is a homogeneous differential equation, same degree in x and y

Question 10.
Solve \(\frac { dy }{dx}\) = xy + x + y + 1
Solution: