Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 6 Random Variable and Mathematical Expectation Miscellaneous Problems Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Miscellaneous Problems
Question 1.
The probability function of a random variable X is given by
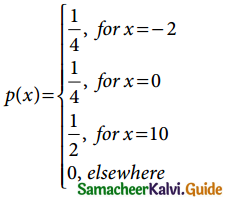
Evaluate the following probabilities.
(i) P(X ≤ 0)
(ii) P(X ≤ 0)
(iii) P( X ≤ 2) and
(iv) P(0 ≤ X ≤ 10)
Solution:
(i) From the data
| x | -2 | 0 | 10 |
| P(x = x) | 1/4 | 1/4 | 1/2 |
(i) P(x ≤ 0) = P( x = -2) + P(x = 0)
= \(\frac { 1 }{4}\) + \(\frac { 1 }{4}\) = \(\frac { 2 }{4}\) = \(\frac { 1 }{2}\)
(ii) P(x < 0) = P(x = -2) = \(\frac { 1 }{4}\)
(iii) P(|x| ≤ 2) = P(-2 ≤ X ≤ 2)
= P(X = -2) + P(X = 0) = \(\frac { 1 }{4}\) + \(\frac { 1 }{4}\)
= \(\frac { 2 }{4}\) = \(\frac { 1 }{2}\)
(iv) p(0 ≤ X ≤ 10) = P (X = 0) + P(X = 10)
= \(\frac { 1 }{4}\) + \(\frac { 1 }{2}\) = \(\frac { 1+2 }{4}\) = \(\frac { 3 }{4}\)
![]()
Question 2.
The probability function of a random variable X is given by
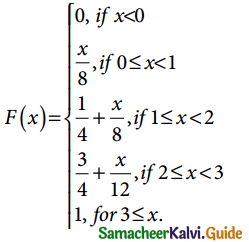
(a) Compute: (i) P(1 ≤ X ≤ 2) and (ii) P(X = 3).
(b) Is X a discrete random variable? Justify your answer.
Solution:
W.K.T Probability density Function
f(x) = \(\frac { d[F(x)] }{dx}\)
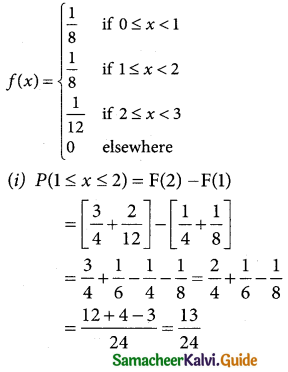
(ii) P(X = 3) = 0
(b) X is not discrete since f is not a step function.
![]()
Question 3.
The p.d.f. of X is defined as
f(x) = \(\left\{\begin{array}{l}
\mathrm{k}, \text { for } 0<x \leq 4 \\
0, \text { otherwise }
\end{array}\right.\)
Solution:
Let X and a random variable if a Probability density function
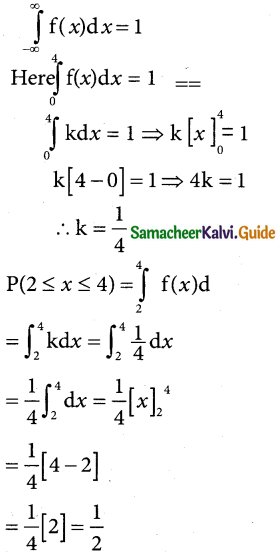
Question 4.
The probability distribution function of a discrete random variable X is
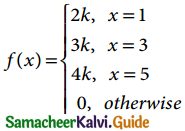
where k is some constant. Find (a) k and (b) P(X > 2).
Solution:
(a) Let X be the random variable of a probability distribution function
W.K.T Σpi = 1
P(x = 1) + P(x = 3) + P(x = 5) = 1
2k + 3k + 4k = 1
9k – 1 ⇒ k = 1/9
(b) P(x > 1) = P(x = 3) + P(x = 5)
= 3k + 4k = 7k
= 7(1/9) = 7/9
![]()
Question 5.
The probability distribution function of a discrete random variable X is
f(x) = \(\left\{\begin{array}{l}
\mathrm{a}+\mathrm{b} x^{2}, 0 \leq x \leq 1 \\
0, \text { otherwise }
\end{array}\right.\)
where a and b are some constants. Find (i) a and b if E(X) = 3/5 (ii) Var(X).
Solution:
Let X be due continuous variable of density function


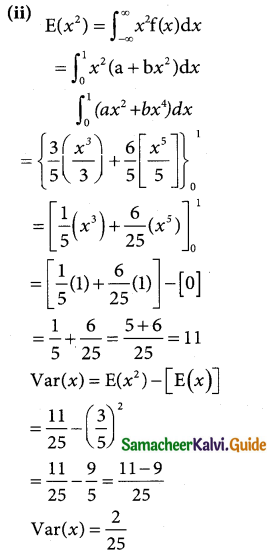
Question 6.
Prove that if E(X) = 0, then V(X) = E(X²)
Solution:
V(X) = E(X²) – [E(X)]²
= E(X²) – 0 {Given that E(X) = 0}
Var(X) = E(X²)
Hence proved.
![]()
Question 7.
What is the expected value of a game that works as follows: I flip a coin and, if tails pay you ₹ 2; if heads pay you ₹ 1. In either case I also pay you ₹ 50.
Solution:
Let x be the remain variable denoting the amount paying for a game of flip coin then x and takes 2 and 1
P(X = 2) = \(\frac { 1 }{2}\) (getting a head)
p(X = 1) = \(\frac { 1 }{2}\) (getting a tail)
Hence the probability of X is
| x | 2 | 1 |
| P(x = x) | 1/2 | 1/2 |
Expected value E(X) = \(\sum_{ x }\)x P(x)
= (2)(\(\frac { 1 }{2}\)) + 1 (\(\frac { 1 }{2}\))
= 1 + \(\frac { 1 }{2}\) = \(\frac { 3 }{2}\)
Since I pay you ₹ 50 in either case
E(X) = 50 × 3/2 = ₹ 75
Question 8.
Prove that, (i) V(aX) = a²V(X) , and (ii) V(X + b) = V(X).
Solution:
LHS = V(ax)
= E(ax)² – [E(ax)]²
= a² E(x²) – [aE(x)]²
= a²E(x²) – a²E(x)]²
= a²E(x²) – E(x)²]
= a²v(x)
= RHS
Hence proved
(ii) LHS = V(x + b)
= E (x + b)² – [E(x + b)]²
= E(x² + 2bx + b²) – [E(x) + b]² –
= E(x²) + 2bE(x) + b² – [E(x)]² + b² + 2bE(x)]
= E(x²) + 2bE(x) + b² -[E(x)]² + b² – 2bE(x)]
= E(x²) – [E(x)]²
= V(x)
= RHS
LHS = RHS Hence proved.
![]()
Question 9.
Consider a random variable X with p.d.f.
f(x) = \(\left\{\begin{array}{l}
3 x^{2}, \text { if } 00 \\
0, \text { otherwise }
\end{array}\right.\)
Find the expected life of this piece of equipment.
Solution:
Let X be the random variable
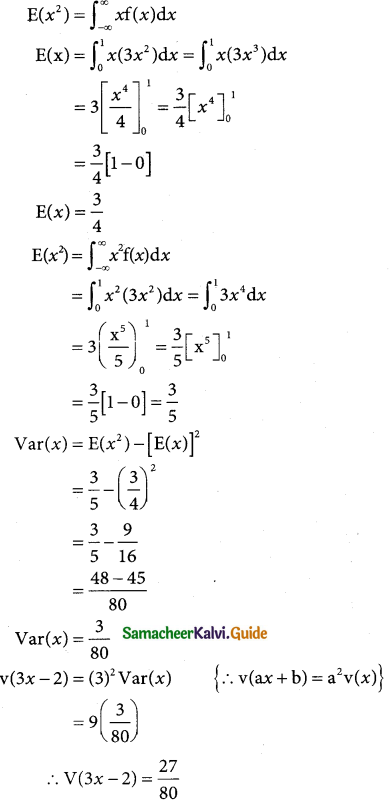
Question 10.
The time to failure in thousands of hours of an important piece of electronic equipment used in a manufactured DVD player has the density function
f(x) = \(\left\{\begin{array}{l}
2 e^{-2 x}, x>0 \\
0, \text { otherwise }
\end{array}\right.\)
Find the expected life of this piece of equipment.
Solution:
Let X be the random variable

![]()