Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 7 Probability Distributions Ex 7.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Ex 7.2
Question 1.
Define possion distribution.
Solution:
Poisson distribution was derived in 1837 by a French Mathematician Simeon D. Poisson.
A random variable X is said to follow a Poisson distribution with parameter X if it assumes only non-negative values and its probability mass function is given by
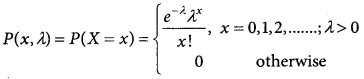
Question 2.
Write any 2 examples for possion distribution
Solution:
1. The number of alpha particles emitted by a radioactive substance in a fraction of a second.
2. Number of road accidents occurring at a particular interval of time per day.
Question 3.
Write the condition for which the possion distribution is limiting case of binomial distribution
Solution:
Poisson distribution is a limiting case of binomial distribution under the following conditions:
(i) n, the number of trials is indefinitely large i.e n → ∞
(ii) p, the constant probability of success in each trial is very small, i.e. p → 0.
(iii) np = λ is finite. Thus p = \(\frac { λ }{n}\) and q = 1 – (\(\frac { λ }{n}\))
where λ, is a positive real number.
Question 4.
Derive the mean and variance of possion distribution.
Solution:
Derivation of Mean and variance of Poisson distribution
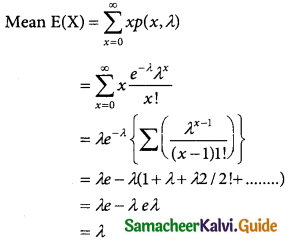
Variance (X) = E(X²) – E(X)²
Variance (X) = E(X²) – E(X)²
= λ² + λ – (λ)²
= λ
Question 5.
Mention the properties of possion distribution.
Solution:
Poisson distribution is the only distribution in which the mean and variance are equal.
Question 6.
The mortality rate for a certain disease is 7 in 1000. What is the probability for just 2 deaths on account of this disease in a group of 400? Give e(-2.8) = 0.06
Solution:
Since the mortality rate for a certain disease in 7 in loop
∴ p = \(\frac { 7 }{1000}\) and n = 400
The value of mean A = λp = 400 × \(\frac { 7 }{1000}\)
∴ λ = 2.8
Let x be a random variable following
distribution with p(x) = \(\frac { e^{-λ}λ^x }{x!}\)
∴ the distribution is p(x = 2) = \(\frac { e^{-2-8}(2.8)^2 }{2!}\)
\(\frac { 0.06×7.84 }{2}\)
= 0.2352
Question 7.
Mention the properties of possion distribution.
Solution:
p(defective bulbs) = \(\frac { 5 }{100}\)
n = 120
The value of mean λ = np = 120 × \(\frac { 5 }{100}\)
λ = 6
Hence, x follows possion distribution with
P(x) = \(\frac { e^{-λ}λ^x }{x!}\)
(x = 0) = \(\frac { e^{-6}(6)^0 }{0!}\) = e-6
= 0.0025
Question 8.
A car hiring firm has two cars. The demand for cars on each day is distributed as a possion variate, with mean 1.5. Calculate the proportion of days on which
(i) Neither car is used
(ii) Some demand is refused
Solution:
In a possion distribution n=2
mean λ = 1.5
x follows poison distribution
With in p(x) = \(\frac { e^{-λ}λ^x }{x!}\)
(i) p(neither car is used) = p(x = 0)
\(\frac { e^{-1.5}(1.5)^0 }{0!}\) = e-1.5
= 0.2231
(ii) p(some demand is refused) = p(x > 2)
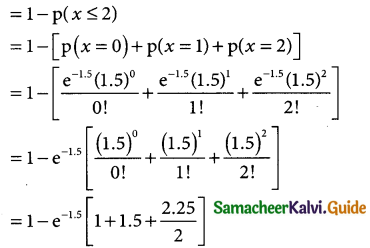
= 1 – 0.2231 [1 + 1.5 + 1.125]
= 1 – 0.2231 [3.625]
= 1-0.8087
= 0.1913
Question 9.
The average number of phone calls per minute into the switch board of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be (i) no phone at all (ii) exactly 3 calls (iii) atleast 5 calls
Solution:
The average number of phone cells per minute into the switch board of a company is λ = 2.5
x follows poisson distribution with
(iii) p(atleast 5 calls) = p(x ≥ 5)
= p(x = 5) + p(x = 6) + …………..
= 1 – p(x < 5)
Question 10.
The distribution of the number of road accidents pre day in a city is possion with mean 4. Find the number of days out of 100 days when there will be (i) no accident (ii) atleast 2 accidents and (iii) at most 3 accidents.
Solution:
In a possion distribution
mean λ = 4
n = 100
x follows possion distribution with
p(x) = \(\frac { e^{-λ}λ^x }{x!}\) = \(\frac { e^{-4}(4)^x }{x!}\)
(i) p(no accident) = p(x = 0)
= \(\frac { e^{-4}(4)^0 }{0!}\) = e-4 = 0.0183
out of 100 days there will be no accident
= n × p(x = 0)
= 100 × 0.0183 = 1.83
= 2 days (approximately)
(ii) p(atleast 2 accidents)
= p(x ≥ 2)
= p(x = 2) + p(x = 3) + p(x = 4) + …………
= 1 – p(x < 2)
= 1 – [p(x = 0) + p(x = 1)]
= 1 – [\(\frac { e^{-4}(4)^0 }{0!}\) + \(\frac { e^{-4}(4)^1 }{1!}\)]
= 1 – e-4 [l + 4]
= 1 – 0.0183(5) = 1 – 0.0915
= 0.9085
= Out of 100 days there will be atleast 2 accidents = n × p(x ≥ 2)
= 100 × 0.9085
= 90.85
= 91 days (approximately)
(iii) p(atmost 3 accident) = p(x ≤ 3)
= p(x = 0) + p(x = 1) + p(x = 2) + p(x = 3)
out of 100 days there will be at most 3 acccident = n × p(x ≤ 3)
= 100 × 0.4331
= 43.31
= 43 days(approximately)
Question 11.
Assuming that a fatal accident in a factory during the year is 1/1200/ calculate the probability that in a factory employing 300 workers there will be atleast two fatal accidents in year, (given e-0.25 = 0.7788 Solution:
Let p be the probability of a fatal accident in a factory during the yeart
p = \(\frac { 1 }{1200}\) and n = 300 1200
λ = np = 300 × \(\frac { 1 }{1200}\) = \(\frac { 1 }{4}\)
λ = 0.25
x follows poison distribution with
p(x) = \(\frac { e^{-λ}λ^x }{x!}\) + \(\frac { e^{-0.25}(0.25) }{x!}\)
p(atleasttwo fatal accidents) = p(x ≥ 2)
= p(x = 2) + p(x = 3) + p(x = 3) + p(x = 4) + ……….
= 1 – p(x < 2)
= 1 – {p(x = 0) + p(x = 1)}
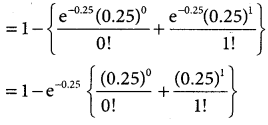= 1 – 0.7788 [1 + 0.25]
= 1 – 0.7788(1.25)
= 1 – 0.9735 = 0.0265
∴ p(x ≥ 2) = 0.0265
Question 12.
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute (i) No customer appears (ii) three or more customers appear.
Solution:
The average number of customers ,who appear in a counter of a certain bank per minute = 2
∴ λ = 2
x follows poisson distribution with
p(x) = \(\frac { e^{-λ}λ^x }{x!}\)
x follows poisson distribution with p(x) = \(\frac { e^{-λ}λ^x }{x!}\)
(i) p(no customber appears) = p(x = 0)
= \(\frac { e^{-2}(2)^0 }{0!}\) = e-2
= 0.1353
(ii) p(three or more customers appears) = p(x ≥ 3)
= p(x = 3) + p{x = 4) + p(x = 5) + ……
= 1 – p(x < 3)
= 1 – {p(x = 0) + p(x = 1) + p(x = 2)}
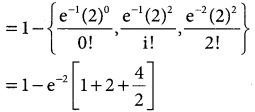
= 1 – 2-2 [1 + 2 + 2]
= 1 – 0.1353(5)
= 1 – 0.6765
= 0.3235