Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 7 Probability Distributions Ex 7.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Ex 7.3
Question 1.
Define normal distribution.
Solution:
A random variable X is said to follow a normal distribution with parameters mean µ and varaince σ², if its probability density function is given by
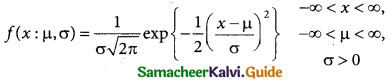
![]()
Question 2.
Define standard normal variate.
Solution:
A random variable Z = (X – µ)/σ follows the standard normal distribution. Z is called the standard normal variate with mean 0 and standard deviation 1 i.e Z – N (0, 1). Its Probability density function is given by:
φ(z) = \(\frac { 1 }{\sqrt {2π}}\) e-x²/2 -∞ < z < ∞
Question 3.
Write down the conditions in which the normal distribution is a limiting case of binomial distribution.
Solution:
The normal distribution of a variable when represented graphically, takes the shape of a symmetrical curve, known as the Normal Curve. The curve is asymptotic to x-axis on its either side.
Question 4. m
Write down any five characteristics of normal probability curve.
Solution:
Chief Characteristics or Properties of Normal Probability distribution and Normal probability Curve.
The normal probability curve with mean µ and standard deviation σ has the following properties:
(i) the curve is bell-shaped and symmetrical about the line x = u.
(ii) Mean, median and mode of the distribution coincide.
(iii) x-axis is an asymptote to the curve, (tails of the curve never touches the horizontal (x) axis)
(iv) No portion of the curve lies below the x-axis as f(x) being the probability function can never be negative.
(v) The points of inflexion of the curve are x = µ ± σ
![]()
Question 5.
In a test on 2,000 electric bulbs, it was found that bulbs of a particular make, was normally distributed with an average life of 2,040 hours and standard deviation of 60 hours. Estimate the number of bulbs likely to burn for
(i) more than 2,150 hours
(ii) less than 1,950 hours
(iii) more 1,920 hours but less than 2,100 hours.
Solution:
Let x denote the burning of the bulb follows normal distribution with mean 2,040 and standard deviation 60 hours.
Here m = 2040; σ = 60 and N = 2000
The standard normal variate
z = \(\frac { x-µ }{σ}\) = \(\frac { x-2040 }{60}\)
(i) p(morethan 2,150 hours)
p(x > 2150)
when x = 2150
z = \(\frac { 2150-2040 }{60}\) = \(\frac { 110 }{60}\)= 1.833
p(x > 2150) = p(z > 1.833)
= p(0 < z < ∞) – p(0 < z < 1.833)
= 0.5 – 0.4664
= 0.0336
∴ Number of bulbs whose burning time is more than 2150 hours=0.0336 × 2000
= 67.2 = 67(approximately)
(ii) p(less than 1950 hours)
p(x < 1950)
when x = 1950
z = \(\frac { 1950-3040 }{60}\) = \(\frac { -90 }{60}\)= -1.5
p(x < 1950) = p(z < -1.5) = p(z > 1.5)
= 0.5 – 0.4332
= 0.068
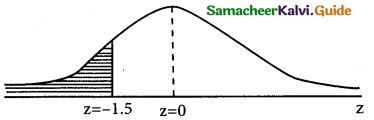
Numbers of bulbs whose burning time is less than
1950 = 0.0668 × 2000 = 133.6
= 134 (approximately)
(iii) p(more 1,920 hours but less than 2,100 hours)
= p(1920 < x < 2100)
when x = 1950
z = \(\frac { 1920-2040 }{60}\) = \(\frac { -120 }{60}\)= -2
when x = 2100
z = \(\frac { 2100-2040 }{60}\) = \(\frac { -60 }{60}\)= -2
∴ p(1920 < x < 2040) = p(-2 < z < 1)
= p(0 < z < 2) + p(0 < z < 1)
= 0.4772 + 0.3413
= 0.8185
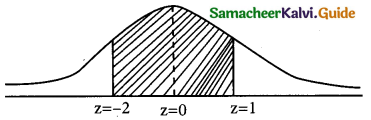
∴ Number of bulbs whose burning time more than 1920 hours but less than 2100 hours) = 0.8185 × 2000
= 1637
![]()
Question 6.
In a distribution 30% of the items are under 50 and 10% are over 86. Find the mean and standard deviation of the distribution.
Solution:
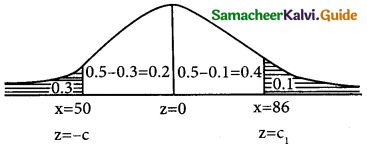
z = \(\frac { x-µ }{σ}\)
Given that
p(x < 50) = 0.3 p(x > 86) = 0.1
p(z < -c) = 0.3
p(-c < z < 0) = 0.5 – 0.3
p(-c < z < 0) = 0.2 {from the table}
p(0 < z < c) = 0.2
c = 0.53
then -c = -0.53
∴ \(\frac { 50-µ }{σ}\) = -0.53
50 – µ = -0.53σ
µ – 0.53σ = 50 → 1
p(x < 50) = 0.1
p(0 < z < ∞) = -p(0 < z < c1) = 0.1
p(0 < z < ∞) = p(0 < z < c1) + 0.1
0.5 = p(0 < z < c1) + 0.1
p(0 < z < c1) = 0.5 – 0.1
p = (0 < z < c1) = 0.4
c1 = 1.29
∴ \(\frac { 86-µ }{σ}\) = 1.29
86 – µ = 1.29 σ
µ + 1.29σ = 86 → 2
solving eqn 1 & 2
eqn 2 ⇒ m + 1.29σ = 86
eqn 1 ⇒ m + 0.53σ = 50
– + – ………….
………… 1.82 ………… σ = 36 ………….
σ = \(\frac { 36 }{1.82}\) ∴ = 19.78
Substitute σ = 19.78 in eqn 1
µ – 0.53(19.78) = 50
µ -10.48 = 50
µ = 50 + 10.48
µ = 60.48
Mean = 60.48 and standard deviation = 19.78
Question 7.
X is normally distributed with mean 12 and sd 4. Find P (x ≤) 20 and P (0 ≤ x ≤ 12)
Solution:
x is normally distribution with mean 12 and sd 4
∴ µ = 12 and σ = 4
Standard normal variable
z = \(\frac { x-µ }{σ}\) = \(\frac { x-12 }{4}\)
(i) p(x ≤ 20)
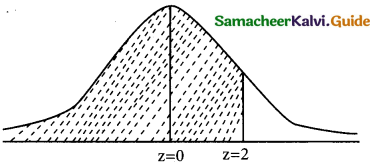
when x = 20
z = \(\frac { 20-12 }{4}\) = \(\frac { 8 }{4}\) = 2
v(x ≤ 20) = \(\frac { 8 }{4}\) = 2
p(x ≤ 20) = p(z ≤ 2)
= 0.5 + p(0 < z < 2)
= 0.5 + 0.4772
= 0.9772
(ii) p(0 < x < 12 )
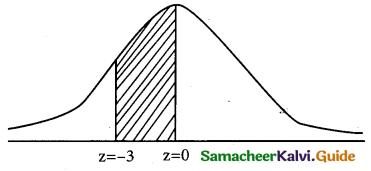
when x = 0
z = \(\frac { 0-12 }{4}\) = \(\frac { -12 }{4}\) = -3
when x = 12
z = \(\frac { 12-12 }{4}\) = \(\frac { 0 }{4}\) = 0
p(0 ≤ x ≤ 12) = p(-3 ≤ z ≤ 0)
= p(0 ≤ z ≤ 3)
= 0.4987
![]()
Question 8.
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height
(a) greater than 2 inches
(b) less than or equal to 64 inches
(c) between 65 and 71 inches.
Solution:
let x denote the height of a student N = 500; m = 68.0 inches and σ = 3.0 inches the standard normal variate
z = \(\frac { x-µ }{σ}\) = \(\frac { x-68 }{3}\)
a(greater than 72 inches)
p = p(x > 72)
when x = 72
z = \(\frac { 72-68 }{3}\) = \(\frac { 4 }{3}\) = 1.33
p(x > 72) = p(z > 1.33)
= 0.5 – 0.4082
= 0.0918
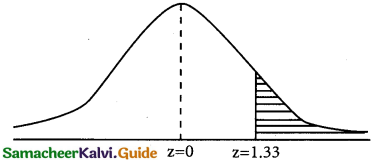
Number of students whose height are greater than 72 inches
= 0.0918 × 500
= 45.9
= 46 (approximately)
(b) p(less than or equal to 64 inches)
p(x ≤ 64)
when x = 64
z = \(\frac { 64-68 }{3}\) = \(\frac { -4 }{3}\) = -1.33
p(x ≤ 64) = p(z ≤ -1.33)
p(z ≥ -1.33)
= 0.5 – 0.4082
= 0.0918
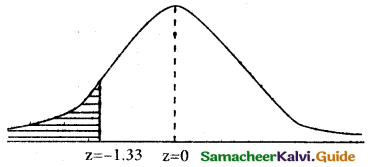
∴ Number of heights whose ate less than or equal to 64 inches =0.0918 × 500
= 45.9
= 46 (approximately)
(c) p(between 65 and 71 inches)
p(65 ≤ x ≤ 71)
when x = 65
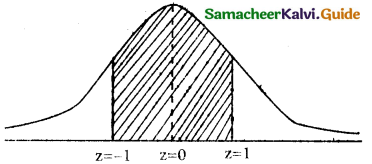
z = \(\frac { 65-68 }{3}\) = \(\frac { -3 }{3}\) = -1
when x = 71
z = \(\frac { 71-68 }{3}\) = \(\frac { 3 }{3}\) = 1
p(65 ≤ x ≤ 71) = p(-1 < z < 1)
= p(-1 < z < 0) + p(0 < z < 1)
= p(0 < z < 1) + p(0 < z < 1)
= 2 × [p(0 < z < 1)]
= 2 × 0.3413
= 0.6826
∴ Number of students whose height between 65 and 7 inches = 0.6826 × 500
= 341.3
= 342 (approximately)
![]()
Question 9.
In a photographic process, the developing time of prints may be looked upon as a random variable having the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second. Find the probability that it will take less than 16.35 seconds to develop prints.
Solution:
let x be the random variable have long the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second
µ = 16,28 and σ = 0.12
The standard normal variate
z = \(\frac { x-µ }{σ}\) = \(\frac { x-16.28 }{0.12}\) = 1
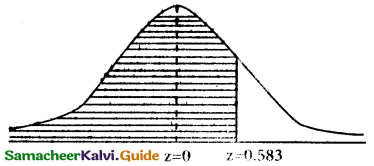
p(less than 16.35 seconds) = p(x < 16.35)
when x = 16.35
z = \(\frac { 16.35-16.28 }{0.12}\) = \(\frac { 0.07 }{0.12}\) = 0.583
p(x< 16.35) = p(z < 0.583)
= p(—∞ < z < 0) + p(0 < z < 0.583)
= 0.5 + 0.2190
= 0.7190
Question 10.
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height (a) greater than 2 inches (b) less than or equal to 64 inches (c) between 65 and 71 inches.
Solution:
Let x be a normal variate with mean 400 labour days and standard deviation of 100 labour days
m = 400 and σ = 100
The construction work should be completed within 450 days.
The standard normal variate
\(\frac { x-µ }{6}\) = \(\frac { x-400 }{100}\)
personality for 1 labour day = Rs 10,000
If personality amount is = 2,00,000 than No of excess
days = \(\frac { 200000 }{10000}\) = 20
∴ x = 450 + 20 = 470
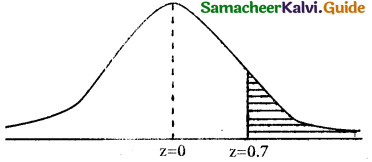
when x = 470
z = \(\frac { 470-400 }{100}\) = \(\frac { 70 }{100}\) = 0.7
= p(x ≥ 470) = p(z ≥ 0.7)
= 0.5 – 0.2580
= 0.2420
(ii) p(at most 500 days) = p(x ≤ 500 )
when x = 500
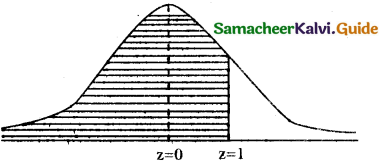
z = \(\frac { 500-400 }{100}\) = \(\frac { 100 }{100}\) = 1
p(x ≤ 500) = p(z ≤ 1)
= p(∞ < z < 0) -r- p(0 < z < 1)
= 0.5 + 0.3415
= 0.8413
![]()