Samacheer Kalvi 12th Maths Guide Chapter 1 Applications of Matrices and Determinants Ex 1.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1

Question 1.
Find the adjoint of the following:

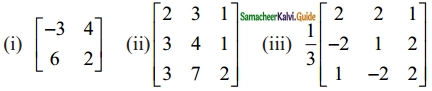
Solution:

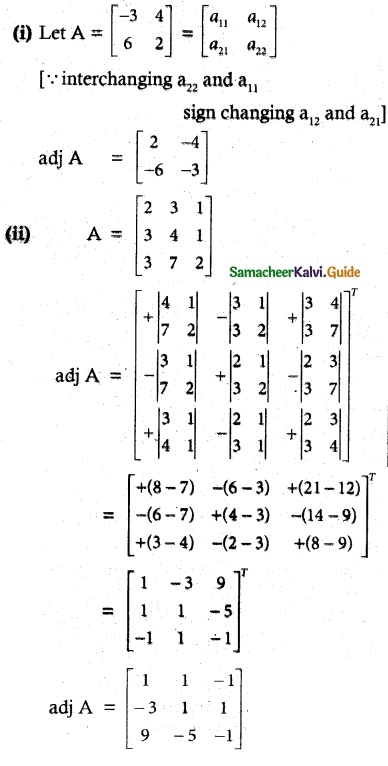
Question 2.
Find the inverse (if it exists) of the following.

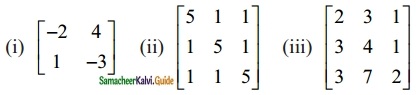
Solution:
\(\begin{bmatrix} -2 & 4 \\ 1 & -3 \end{bmatrix}\)
|A| = 6 – 4 = 2 ≠ 0
∴ A^-1 exists. A is non singular.


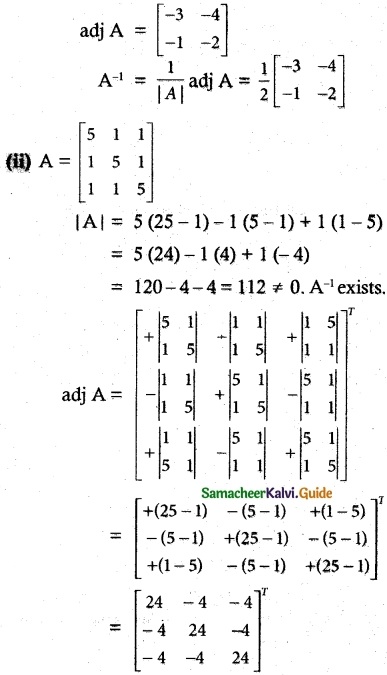
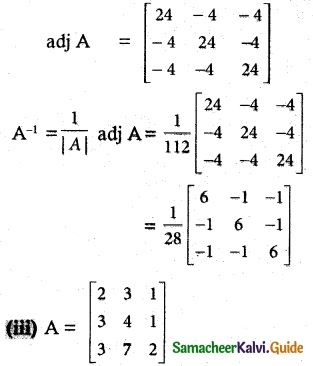
|A| = 2(8-7)-3(6-3)+1(21-12)
= 2 – 9 + 9 = 2 ≠ 0. A^-1 exists.

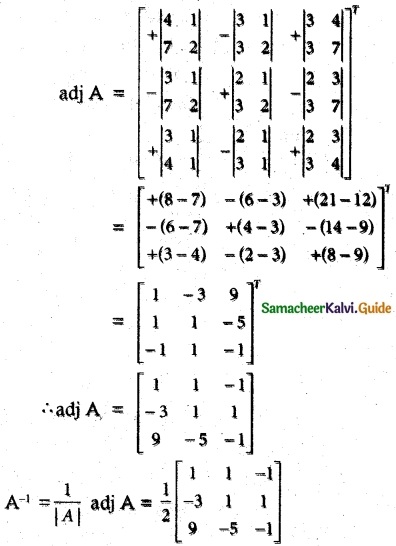
Question 3.

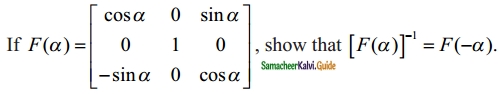
Solution:
\(\left[\begin{array}{ccc}
\cos \alpha & 0 & \sin \alpha \\
0 & 1 & 0 \\
-\sin \alpha & 0 & \cos \alpha
\end{array}\right]\)
|F(α)| = cos α(cos α – 0) – 0 + sin α(0 + sin α)
= cos²α + sin²α = 1
|f(α)| = 1 ≠ 0. [F(α)]^-1 exists.


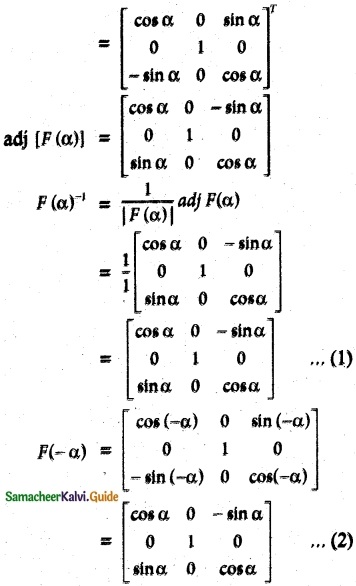
[∵ cos (-θ) = cos θ ; sin(-θ) = -sin θ]
from (1) and (2) we have
[F(α)]^-1 = F(-α)

Question 4.
If A = \(\begin{bmatrix} 5 & 3 \\ -1 & -2 \end{bmatrix}\), show that A² – 3A – 7I₂ = O₂. hence find A^-1
Solution:

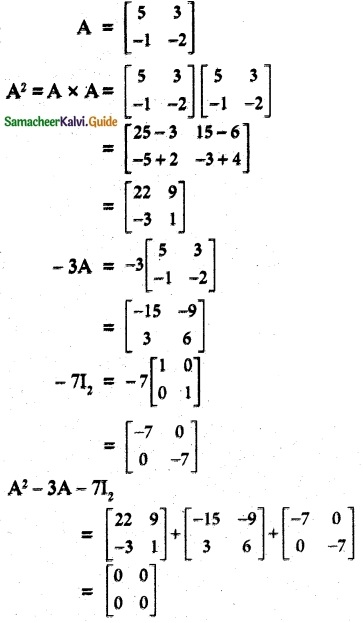
∴ A² -3A – 7I₂ = O₂
Post multiply this equation by A^-1
A²A^-1 – 3A A^-1 – 7I₂ A^-1 = 0
A – 3I – 7A^-1 = 0
A – 3I = 7 A^-1
A^-1 = \(\frac {1}{7}\) (A – 3I)

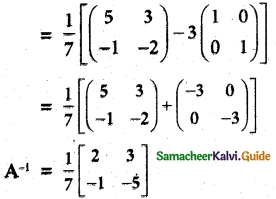
Question 5.

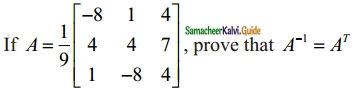
Solution:

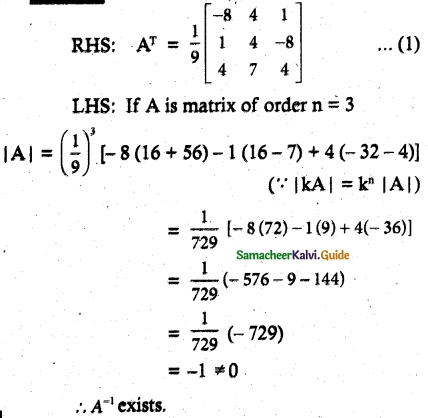
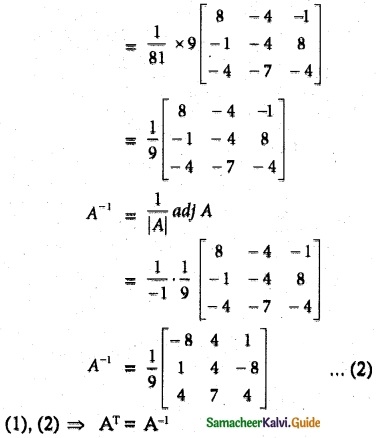
Question 6.
If A = \(\begin{bmatrix} 8 & -4 \\ -5 & 3 \end{bmatrix}\) verify that A(adj A) = (adj A) A = \(\left| A \right|\)I₂.
Solution:

(1), (2) and (3) ⇒ A (adj A) = (adj A)A = |A| I₂.

Question 7.

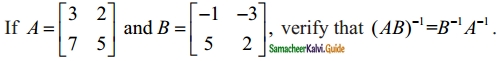
Solution:

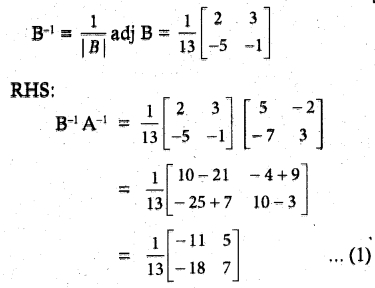
Question 8.

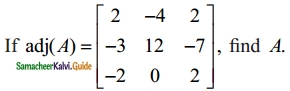
Solution:

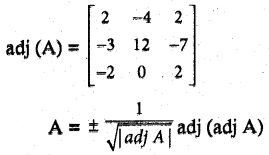
|adj (A)| = 2 (24 – 0) + 4 (- 6 – 14) + 2(0 + 24)
= 48 – 80 + 48 = 16

Question 9.

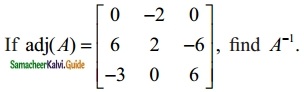
Solution:

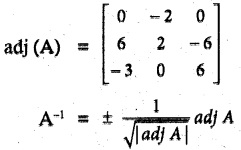
|adj A| = 0 + 2(36 – 18) + 0 = 2(18) = 36

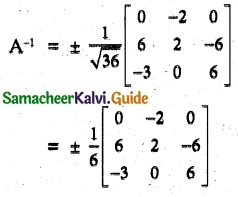
Question 10.

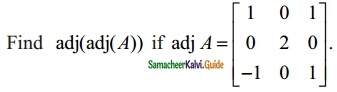
Solution:

Question 11.

Solution:


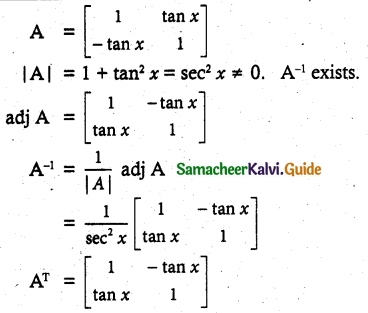
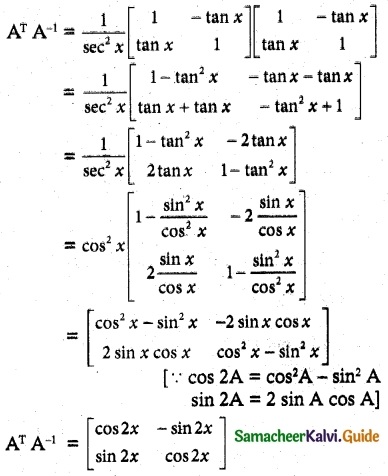
Hence proved

Question 12.

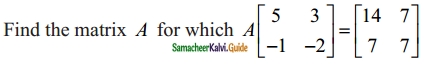
Solution:

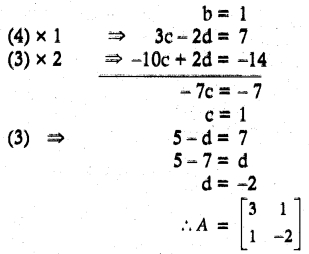
Question 13.

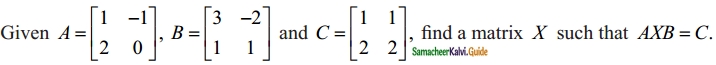
Solution:
Given A × B × C
⇒ A^-1 A × B B^-1 = A^-1 C B^-1
I × I = A^-1 C B^-1
⇒ X = A^-1 CB^-1
let us find A^-1 and B^-1

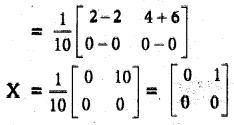
Question 14.

Solution:


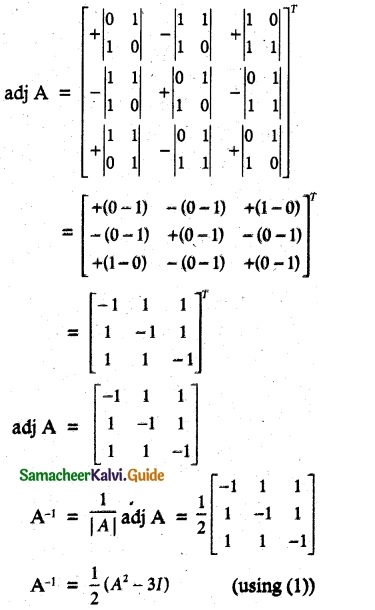
Hence proved.

Question 15.
Decrypt the received encoded message [2 -3] [20 4] with the encryption matrix \(\begin{bmatrix} -1 & -1 \\ 2 & 1 \end{bmatrix}\) and the decryption matrix as its inverse, where the system of codes are described by the numbers 1 – 26 to the letters A – Z respectively, and the number 0 to a blank space.
Solution:

So the sequence of decoded row matrics is [8 5] [12 16]
The receiver reads the message as “HELP”.